一种针对异常点的自适应回归特征选择方法

郭亚庆 王文剑 苏美红

1(山西大学计算机与信息技术学院 太原 030006)2(计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006)

一些实际学习任务的数据集中常含有大量不相关特征和冗余特征，特征数目巨大，如基因组分析、文本分类和图像检索等，故会导致维数灾难和学习任务难度提高等问题，以至于学习效果不好或学得模型可解释性差.此外，观测某些特征代价昂贵，若这些特征为无关特征，则会造成大量不必要开销.解决上述问题的一种有效途径是特征选择.特征选择是将可以代表整体的含有关键性度量信息的部分特征挑选出来的过程，它使得后续学习过程仅需在一部分特征上构建模型[1-2].另外，现有针对回归问题的特征选择方法，当数据集含异常点时，对其敏感或自适应能力不佳，导致特征选择和学习效果较差.故如何自适应地进行稳健回归特征选择仍然是一个挑战性的课题.

针对分类问题的特征选择方法已有很多，常用的方法可分为2类:一类为过滤式(如Relief(relevant features)、mRMR(max-relevancy, min-redundancy)和Relief-F等);另一类为包裹式(如LVM(Las Vegas wrapper)、SFFS(sequential floating forward selection)、SFS(sequential feature selection)和LRS(Plus-L-Minus-R search)等)[3-6].这些方法都是先对数据集进行特征选择，再训练学习器，其中过滤式方法特征选择过程与后续学习器无关，导致最终学习器性能不好；包裹式方法虽然在选择特征时考虑了学习器性能，但因为多次训练学习器造成了大量时间开销.

上述面向分类的特征选择方法往往不能直接用于回归问题或应用后效果不好.目前针对回归问题的特征选择方法较少，其代表性方法分为两大类：

1) 先对数据集进行特征选择，然后再训练学习器，如向前选择法(forward-stepwise selection)、向后剔除法(backward-stepwise selection)和逐步筛选法(forward-stagewise regression)等，这些方法不仅具有分类特征选择方法的某些缺点，还不适用于特征数目巨大和有相关特征的数据集，适用范围较小，故并不常用[7].

2) 将特征选择过程与学习器训练过程融为一体同时完成，提高了最终学习器的性能，降低了开销，其典型方法有LASSO[8]、LAD-LASSO(least absolute deviation)[9]、L1/2正则化[10]、岭回归(ridge regression)[11]、Elastic Net[12]、Group Lasso[13]、SCAD(smoothly clipped absolute deviation)[14]和MCP(minimax concave penalty)[15]等.其中岭回归因使用L2正则项而不易于获得稀疏解；L1/2正则化的实现算法效率较低；Elastic Net适用于特征之间相关性较高的数据集；Group Lasso适用于协变量之间存在组结构的回归数据集；SCAD和MCP虽然降低了LASSO的泛化误差，但正则项复杂，较难求解，故LASSO和LAD-LASSO这2种方法更为常用.LASSO可以较为准确地完成特征选择，并且计算快捷，故被广泛使用.

上述回归特征选择方法对异常点(数据集中与数据的一般行为或模型不一致的数据对象)极其敏感，导致对于含有异常点的数据集，其稳健性和稀疏性都有所下降.目前提出的稳健回归特征选择方法不多且大多针对含有噪声的数据集，如分位数回归及其改进方法[16-18]和LAD-LASSO等，其中分位数回归及其改进方法模型复杂.针对异常点的稳健回归估计方法有WLAD(weight least absolute deviation)[19]和LTS(least trimmed squares estimator)[20]等，在其基础上WLAD-LASSO[19],LTS-LASSO[20],reweighted LTS-LASSO[20],WLAD-CATREG(categorical regres-sion model) adoptive elastic net[21]和WLAD-SCAD[22]等被相继提出，这些方法增加了易于获得稀疏解的正则项，可以同时完成特征选择和学习器训练.其中LTS-LASSO通过将训练误差较小的数据集子集作为训练集来降低异常点影响，但其时间开销较大；其余针对异常点的回归特征选择方法通过给损失函数加权来提高其稳健性，其中reweighted LTS-LASSO将LTS-LASSO求得的回归系数作为参数初值，WLAD-LASSO,WLAD-CATREG和WLAD-SCAD根据数据集稳健位置估计量、数据集散点估计量和各样本的稳健距离得样本权重，上述通过加权来提高稳健性的回归特征选择方法都是先计算好样本损失函数权重，再进行特征选择和学习器训练，样本权重在整个算法执行过程中固定不变，故它们无法在特征选择和学习器训练过程中根据学习效果多次自主修改权重来进一步提高算法性能，算法自适应能力不佳.此外，针对现有回归特征选择方法当数据集含异常点时性能较差这一固有问题，近年来并没有很好的研究成果.

鉴于此，本文提出一种能不断根据数据集和学习效果自主更新样本权重的用于线性回归的稳健特征选择方法AWLASSO(adaptive weight LASSO)，其使用在[0,1]中连续变化的自适应权重以更好地提高自适应性.该方法将特征选择与学习器训练过程融为一体同时完成，以提高学习器性能和降低模型复杂度.AWLASSO算法通过阈值确定样本的损失函数权重;一方面可以使迭代过程总朝着较好的回归系数估计值方向进行；另一方面能保证训练集含有足够的样本，同时可以排除异常点的影响.本文在构造数据和标准数据上验证了提出方法的有效性.

1 预备知识

为便于理解本文提出方法及与LASSO和LAD-LASSO进行比较，本节简要介绍LASSO和LAD-LASSO.

(1)

其中，正则化参数λ>0.求解LASSO的方法有Homotopy[23]、LARS(Least Angle RegresSion)[24]、坐标下降法[25-26]等.

与LASSO方法相比，LAD-LASSO方法以绝对值误差为损失函数，其优化目标为

(2)

将其转化成线性规划问题即可求解[27].

2 针对异常点的自适应回归特征选择方法

2.1 AWLASSO模型

对于不含异常点的数据集，LASSO和LAD-LASSO方法都具有良好的性能，然而对于含有异常点的数据集，这2种方法没有区别对待异常点，可能使得回归系数估计值与真实回归系数相差较大，导致特征选择和学习器训练效果不好.此外，LASSO使用平方误差作为损失函数，相比LAD-LASSO以绝对值误差为损失函数，可能会使异常点的影响被放大，故其稳健性和稀疏性被破坏更为严重.

本文提出的AWLASSO首先根据更新后的回归系数更新样本误差，并通过自适应正则项将误差大于当前阈值的样本的损失函数赋予较小权重，误差小于阈值的样本的损失函数赋予较大权重，再在更新了权重的加权损失函数下重新估计回归系数.通过不断迭代上述过程，它每次在较优样本权重估计值下完成回归系数估计，在较优回归系数估计值下完成样本权重估计.多次自主修正权重后其在合适的加权损失函数下完成特征选择和学习器训练.本文在第1次迭代时随机挑选部分样本作为训练集，该训练集可能含有异常点，故为防止异常点进入下一次迭代，在下一轮迭代中得到较好的回归系数估计值，AWLASSO阈值初始值取较小值.在上述迭代过程中，阈值不断增大，被误判为异常点的样本有机会重新进入训练集，以保证训练集含有足够的样本和保留多种样本信息.相比阈值由大到小进行迭代，上述阈值选取方式，大量异常点进入训练集的可能性较小，不会出现即使减小阈值，由于各样本误差累积，仍无法对样本损失函数准确赋权重，最终得到偏差较大的回归系数估计值的情况.AWLASSO当达到最大阈值时迭代停止，此时它将误差大于最大阈值，即学习代价较大，会严重影响学习效果的样本视作异常点，令其损失函数权重为0，以降低异常点的影响.

AWLASSO具体模型为

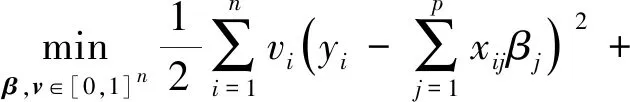
(3)

1) 更新样本权重.首先根据当前的回归系数估计值更新各样本误差，然后更新自适应正则化参数，最后利用更新后的各参数和自适应正则项更新样本权重，此时，误差大于当前阈值的样本的损失函数被赋予较小权重，误差小于阈值的样本的损失函数被赋予较大权重，并利用更新后的权重修正加权损失函数.

2) 更新回归系数.求解更新后的目标函数，即完成特征选择和学习器训练，并反馈回归系数估计值.

AWLASSO算法多次迭代上述2个阶段，不断根据数据集和学习效果自主更新样本权重.在上述迭代过程中，阈值不断增大，当达到最大阈值时迭代停止，此时AWLASSO将误差大于最大阈值的样本视作异常点，令其损失函数权重为0，以降低异常点的影响，提高算法性能.其在处理异常点时，不仅不需要较好地回归系数参数初值，也不只依赖数据集，算法具有较好的自适应能力.

2.2 样本权重确定

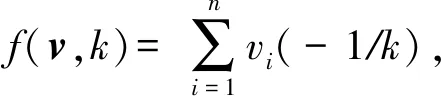
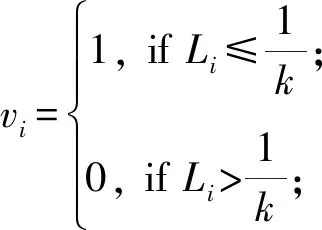
(4)

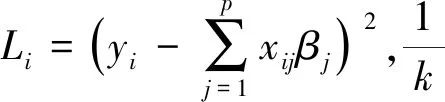
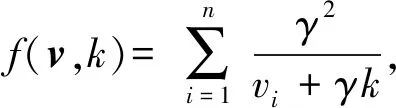
通过优化

可得自适应向量各分量为

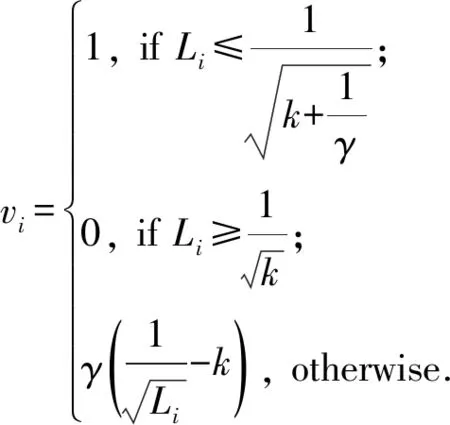
(5)

2.3 模型求解

本文使用交替迭代方法求解AWLASSO模型，每次迭代先固定v求β，再固定β求v，直到获得较为满意的结果为止.固定v求β时，AWLASSO的优化目标为

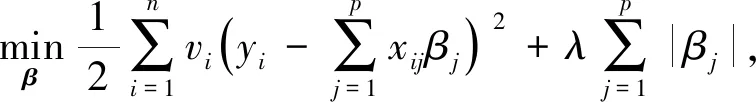
(6)

与常规的LASSO相同，本文也选用坐标下降法[25]求解该优化目标，即：

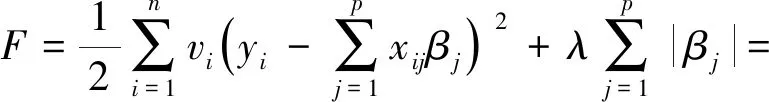
对βj求导得：

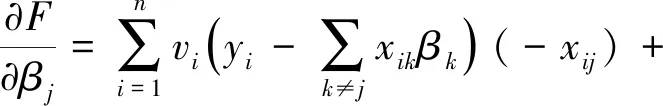
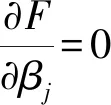
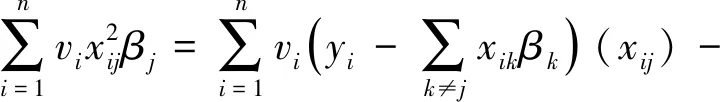
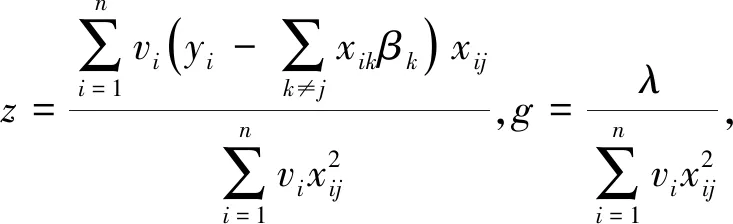
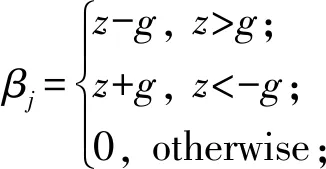
(7)

其中,βj∈[0,z)或(z,0]，且当z≠0时βj与λ有关，当λ值较大时，βj有可能成为0.

在下次迭代过程中，通过式(5)更新v.

2.4 算法描述

求解AWLASSO的主要步骤如算法1所示.

算法1.AWLASSO模型求解算法.

输入：训练集X∈Rn×p和Y∈Rn、自适应参数初始值k0、自适应参数终止值kend、正则化参数λ,且k0>kend,μ>1;

输出：回归系数β.

Step1. 初始化自适应向量v为一个固定值(一般随机令v一半分量为0，另一半分量为1)，自适应参数k=k0；

Step2. 当自适应参数k>kend时，循环执行以下步骤：

Step2.1. 更新回归系数β；

Step2.3. 将各参数带入式(5)，更新v；

3 实验结果及分析

3.1 数据集及评价指标

为验证本文提出方法AWLASSO的有效性，分别在2个构造数据集和4个标准数据集上进行实验，并与LASSO和LAD-LASSO进行对比.

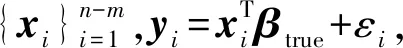
Table 1 Artificial Datasets表1 构造数据集

Table 2 Benchmark Datasets表2 标准数据集

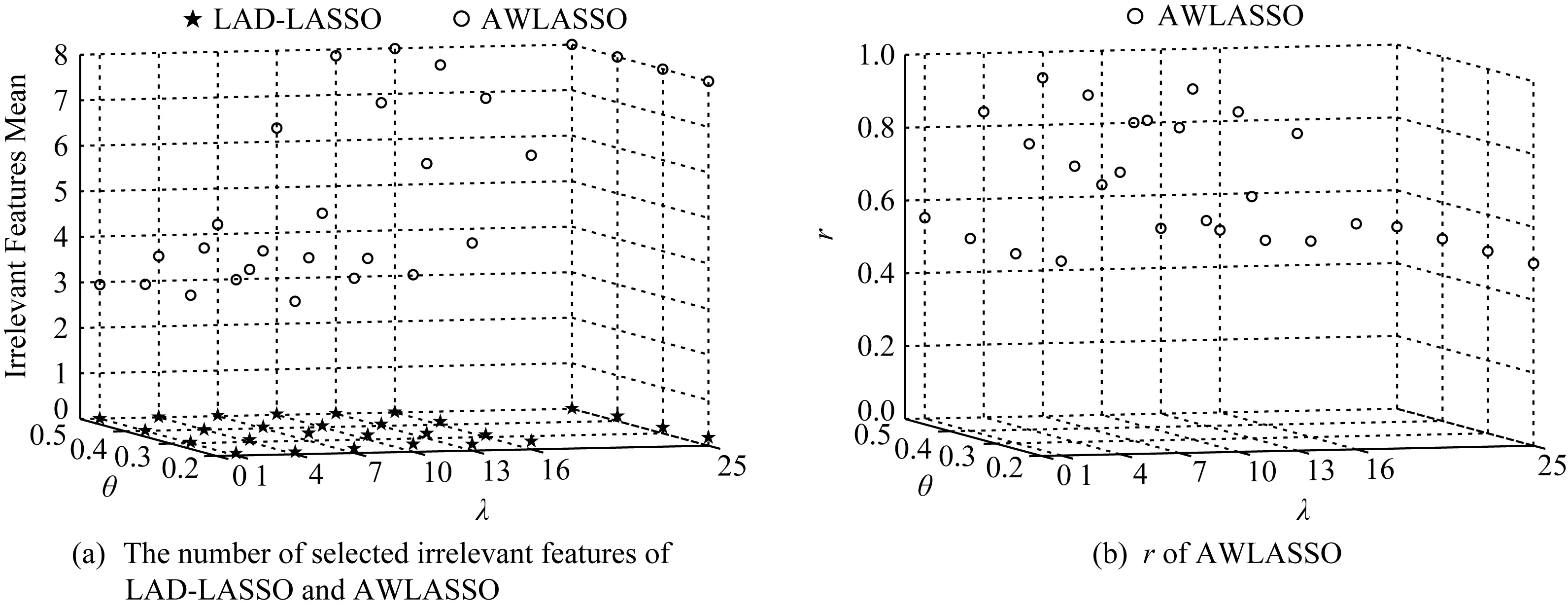
Fig. 1 Feature selection results on D1图1 在D1数据集上的特征选择结果

实验中AWLASSO方法的参数γ=0.4，μ=1.2，k初始值为2.5，终止值为0.000 1.在构造数据集上，实验重复进行100次，取平均值作为最终结果.

本文用平均平方误差(MSE)作为评价算法稳健性的性能指标，用MSE1表示回归系数估计值β*与βtrue的差别，即：

(8)

用MSE2表示回归系数估计值β*与βfalse的差别，即：

(9)

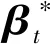
(10)

其中,w表示实验重复次数，Yt表示第t次实验得到的回归向量预测值.如果某种方法的MSE1较小且MSE2较大或MSE3较小，说明该方法估计出的回归系数与真实回归系数相差较小，与干扰回归系数相差较大，其稳健性较好，反之稳健性较差.同时本文用无关特征选择正确个数的平均表现来评估这3种方法的稀疏性，其值越接近真实回归系数含0总数，对应方法稀疏性越好，反之则越差.

所有实验用MATLABR2014a实现.实验环境为4 GB内存，Intel®CoreTM2 Quad处理器，2.66 GHz，Windows10操作系统.

3.2 构造数据集上的实验结果

3.2.1 特征选择结果

首先比较LASSO，LAD-LASSO和AWLASSO这3种方法特征选择的结果.由于这3种方法在构造数据集D1和D2上特征选择结果基本一致，故本文只给出构造数据集D1上的实验结果.图1为构造数据集D1上的特征选择结果，图1(a)是选出无关特征的个数的平均结果，图1(b)给出了无关特征选择正确个数的平均结果与选出无关特征的个数的平均结果的比例r.在D1数据集上，真实回归系数有4个分量为0，即有4个无关特征，故在图1(a)中选出无关特征的个数的平均结果越接近4，对应方法特征选择效果越好.由于LASSO在各污染率下无关特征选择正确个数的平均结果和选出无关特征的个数的平均结果皆为0，且LAD-LASSO和AWLASSO在各污染率下当λ>25时，得到的回归系数估计值各分量皆为0或极小的数，方法失效，故未在图1中给出上述实验特征选择结果.从图1(a)中可以看出，在不同污染率下，LASSO和LAD-LASSO在不同λ值下选出无关特征的个数的平均结果都接近于0，严重偏离4；AWLASSO当λ取值较小时接近于4.由于LAD-LASSO并未完成特征选择，图1(b)只给出AWLASSO方法的r，r值应介于0到1之间.由图1(b)可知AWLASSO方法当选出无关特征的个数的平均结果接近于4时其r都接近于1，即它正确选出了无关特征，特征选择结果较好，但它对参数λ较为敏感，当λ值增大到一定程度后，其得到的回归系数估计值各分量都为0，r=1/2，无法完成特征选择.

3.2.2 稳健性比较

本文还比较了3种方法的稳健性.由于这3种方法在构造数据集D1和D2上实验结果基本一致，故本文只给出构造数据集D2上的实验结果.图2是构造数据集D2在不同污染率下MSE1和MSE2的比较结果，其中不含空心圆的曲线表示各方法的MSE1，含空心圆的曲线表示各方法的MSE2.从图2中可以看出，在不同污染率下，无论是MSE1还是MSE2，LASSO方法都较大，说明其对含有异常点的数据处理能力较差.对于MSE1，AWLASSO方法在一定的λ值之下，都小于LAD-LASSO，当λ值继续增大时，LAD-LASSO的MSE1才减小至与AWLASSO的相同.对于MSE2，在绝大多数情况下AWLASSO要高于LAD-LASSO，当λ大于一定值之后，2种方法的MSE2才相同.实验结果表明，AWLASSO方法估计出的回归系数都与回归系数真实值相差较小(MSE1较小)，与干扰回归系数相差较大(MSE2较大)，它不会像LAD-LASSO方法那样受干扰回归系数的影响，故AWLASSO方法的稳健性更好.

Fig. 2 Comparisons of MSE1 and MSE2 on D2图2 3种方法在D2数据集上的MSE1和MSE2比较结果

为了更好地说明AWLASSO方法与LAD-LASSO方法的稳健性，通过对比图2各分图可得它们在构造数据集D2上污染率取不同值时MSE1的比较结果.从中可以看出，当其他参数取值相同时，LAD-LASSO方法对应的MSE1随着污染率的增大而显著增大，AWLASSO方法对应的MSE1并没有随着污染率的增大而显著增大，而是一直处于某一值附近，其性能不会随着数据集中被污染数据的增加而显著变差，即AWLASSO方法相比LAD-LASSO方法更稳健.

在构造数据集上的所有实验结果表明：无论数据分布如何，异常点分布如何，AWLASSO都比LASSO和LAD-LASSO更稳健更稀疏.

3.3 标准数据集上的实验结果

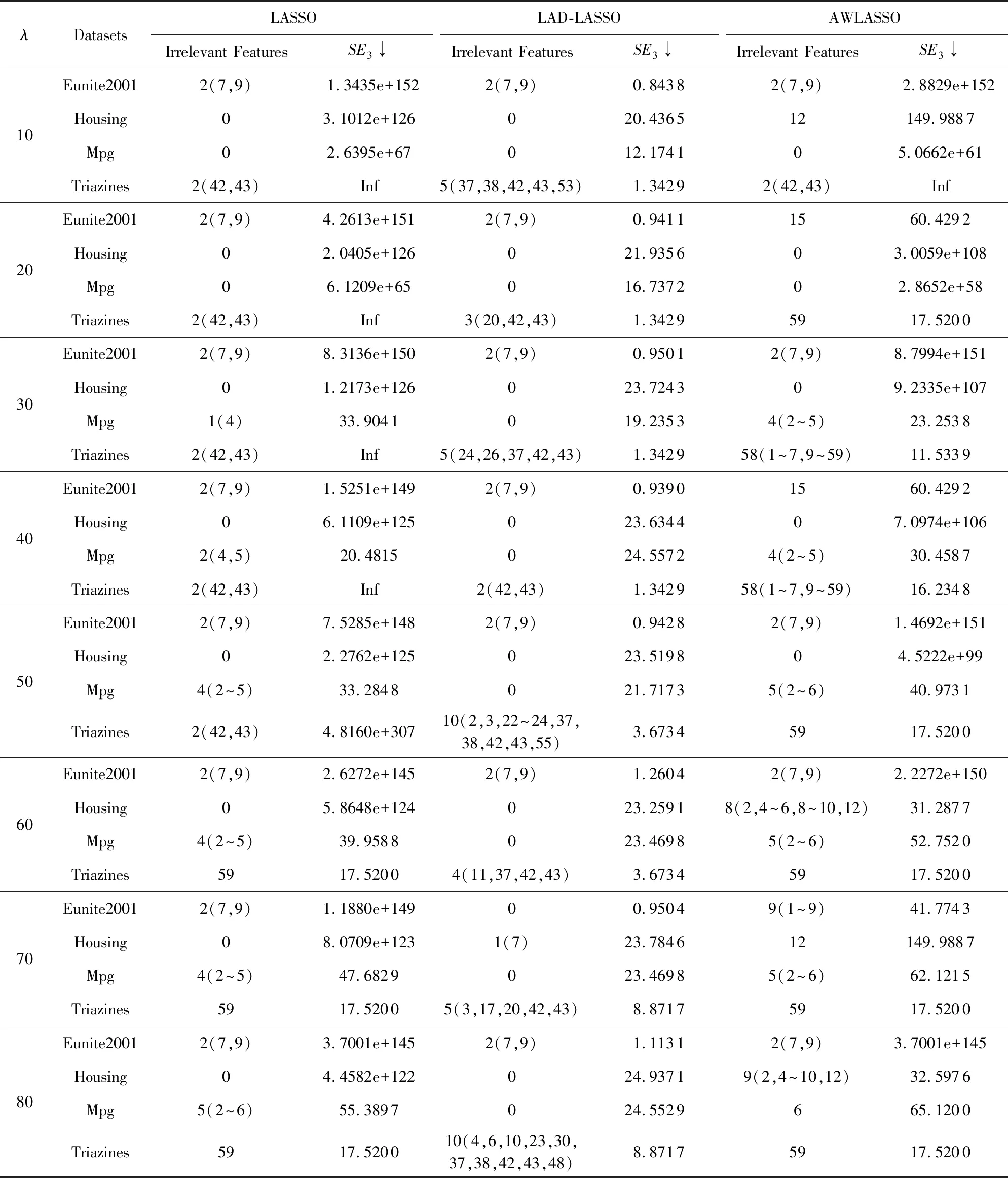
Table 3 Experiment Results of Three Methods on Benchmark Datasets表3 3种方法在标准数据集上的实验结果

Note: “↓” represents the most robust method is the one having the lowestSE3.

1) 原始数据集上的实验结果

由表3知，LASSO在上述标准数据集上的32个回归系数估计值中有10个不含无关特征，LAD-LASSO的有16个不含无关特征，AWLASSO的有6个不含无关特征.AWLASSO在Eunite2001数据集上，当λ=70时，选出了9个无关特征；在Housing数据集上，当λ=80时，选出了9个无关特征；在Mpg数据集上，当λ=50时，选出了5个无关特征；在Tiazines据集上，当λ=30时，选出了58个无关特征，即其在各数据集上选出无关特征最多，且没有将所有特征视作无关特征.在各数据集上，AWLASSO方法对参数λ较为敏感，它只在某些λ值下特征选择效果好，学习器训练效果中等；LAD-LASSO方法在各λ值下学习器训练效果都好，但特征选择效果都不好；LASSO方法在数据集Eunite2001,Housing和Triazines上，特征选择和学习器训练效果都不好，但在数据集MPG上，当参数λ取某些值时，其特征选择和学习器训练效果较好.

由于LASSO方法整体表现不稳定，所以后边实验只比较了LAD-LASSO和AWLASSO方法的性能.表4给出了这2种方法在各自较优参数范围内的实验结果比较，“0”表示在较优参数范围内求得的各回归系数估计值无重叠无关特征.由表4知，当参数λ在较优参数范围内时，LAD-LASSO方法在4个数据集上都没有重叠无关特征，它在各较优参数λ下只有少数回归系数估计值含有少量0分量，其选出的无关特征较少.AWLASSO在所有的数据集上都有大量重叠无关特征，其在较优参数范围内得到的各回归系数都含大量的0分量，它选出了大量无关特征且不会将所有特征视作无关特征.AWLASSO方法的最小SE3和最大SE3要稍大于LAD-LASSO方法的.故在标准数据集上AWLASSO没有LAD-LASSO稳健，但比LAD-LASSO稀疏.

2) 含异常点数据集上的实验结果

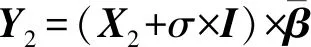
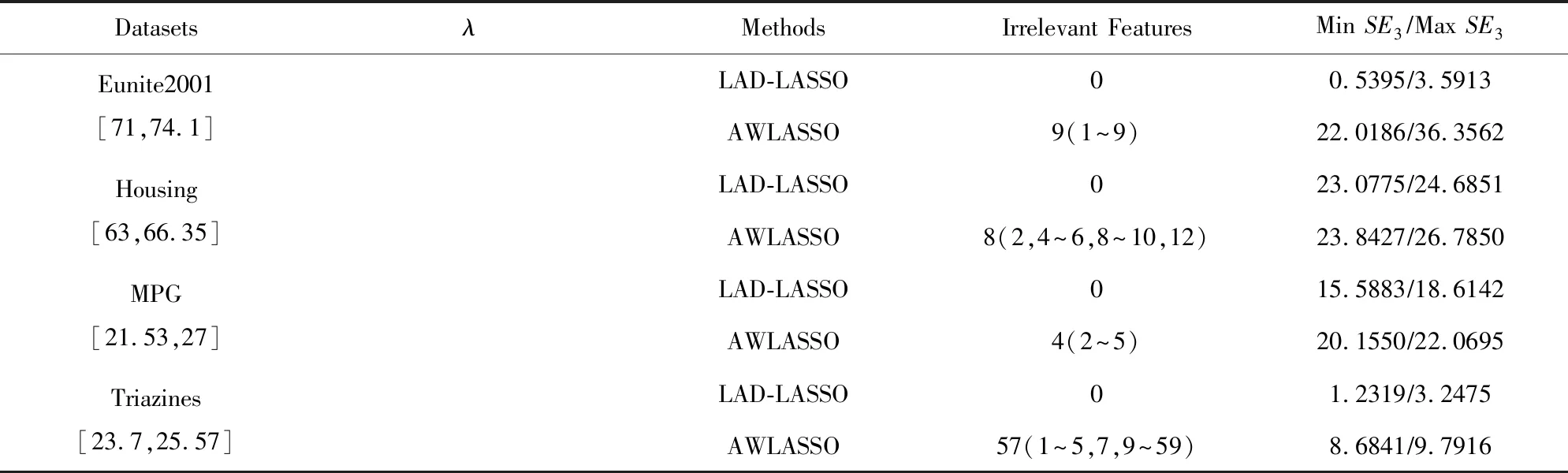
Table 4 Experiment Results with Fitted Parameter λ on Benchmark Datasets表4 较优参数λ下的标准数据集实验结果

由表5可知，在上述标准数据集上，LAD-LASSO在各θ下的50个回归系数估计值都没有重叠无关特征.它在各数据集上所有参数组合下的200个回归系数估计值，在Eunite2001上有174个不含无关特征，有26个有无关特征但无重叠无关特征；在Housing数据集上有193个不含无关特征，有7个有无关特征但无重叠无关特征；在Triazines数据集上有75个不含无关特征，有125个有无关特征但无重叠无关特征；在MPG数据集上有197个不含无关特征，有3个有无关特征但无重叠无关特征.而AWLASSO只在MPG数据集上当污染率θ=0.5时没有重叠无关特征，剩余情况下，其皆有大量重叠无关特征，而且它重叠无关特征数小于数据集特征总数，即AWLASSO没有将所有特征视作无关特征.

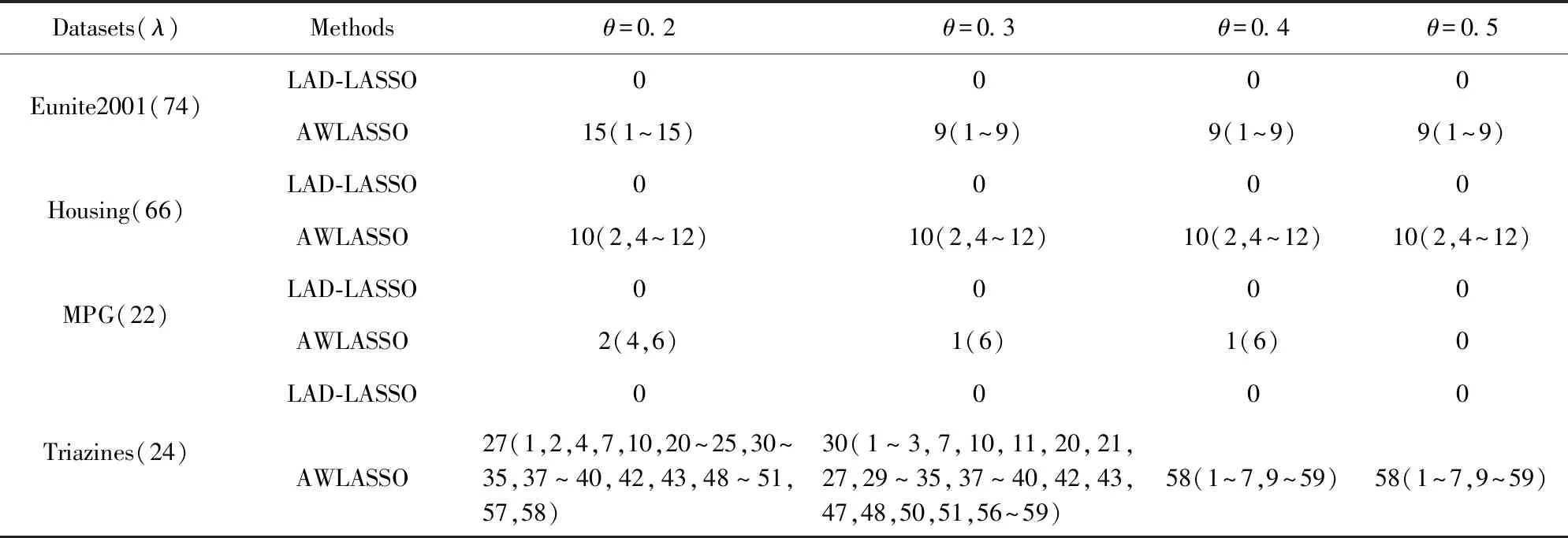
Table 5 Feature Selection Results on Benchmark Datasets with Outliers表5 含异常点的标准数据集特征选择结果

Fig. 3 Comparisons of MSE3 on benchmark datasets with outliers图3 含异常点的标准数据集上MSE3的比较结果

由图3可知当异常点含量为20%时，AWLASSO方法只在MPG数据集上MSE3比LAD-LASSO的小，但在Triazines数据集上两者MSE3相差不大.当异常点含量为30%～50%时，AWLASSO方法的MSE3要比LAD-LASSO的小很多，且它不会像LAD-LASSO那样其MSE3随着污染率的增大而显著增大.在标准数据集上的实验结果表明当数据集含异常点时，AWLASSO方法的特征选择能力更强、稳健性更好.

3.4 高维数据集上的实验结果

为验证AWLASSO方法在特征数量较多的数据集上的性能，本文构造高维数据集D3和D4，其构造方法与构造数据集的构造方法相同.高维数据集的真实回归系数βtrue=(1,2.5,1.5,2,0,…,0)T，数据集如表6所示：

Table 6 High Dimensional Datasets表6 高维数据集

高维数据集上LASSO，LAD-LASSO和AWL-ASSO这3种方法特征选择的结果如图4所示.由于LASSO未完成特征选择，故在图中未给出其结果.由图4(a)(b)可知，当λ取合适值时，LAD-LASSO几乎没有选出无关特征，AWLASSO在D3和D4数据集上选出无关特征数目的均值接近于数据集所含无关特征总数，且它正确选出了无关特征.

图5和图6分别是3种模型在不同污染率下MSE1和MSE2的比较结果.从图5和图6中可以看出，在不同污染率下，相比LASSO和LAD-LASSO，绝大多数情况下AWLASSO方法MSE1都较小，MSE2都较大，且其对应的MSE1并没有随着污染率的增大而显著增大.高维数据集上的实验结果表明，当数据集含大量特征时，AWLASSO方法仍有较好的稳健性和特征选择能力.

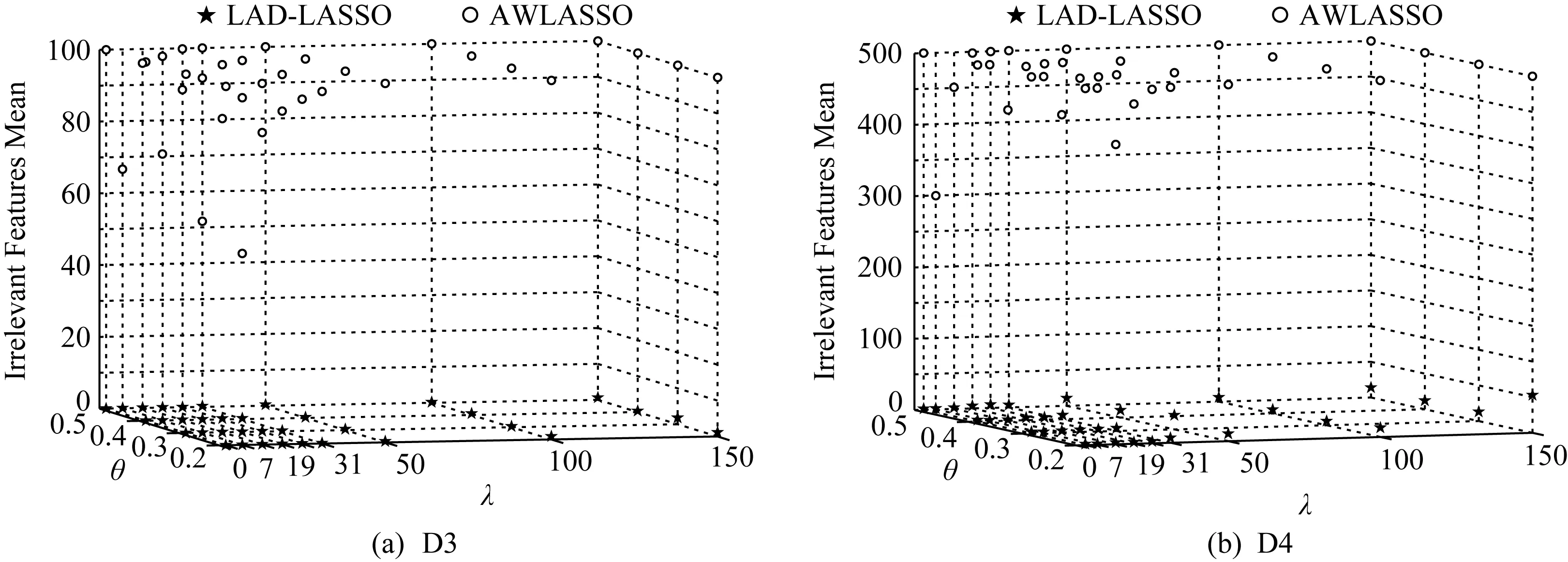
Fig. 4 Feature selection results on high dimensional data sets图4 在高维数据集上的特征选择结果

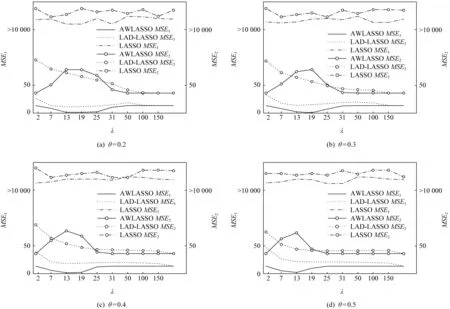
Fig. 5 Comparisons of MSE1 and MSE2 on D3图5 3种方法在D3数据集上的MSE1和MSE2比较结果

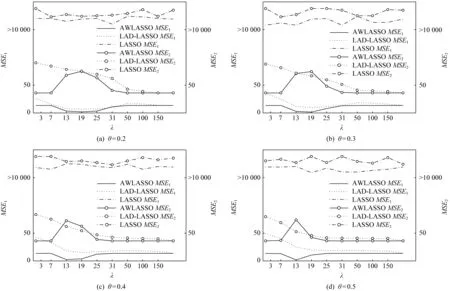
Fig. 6 Comparisons of MSE1 and MSE2 on D4图6 3种方法在D4数据集上的MSE1和MSE2比较结果

4 结 语

目前针对回归问题的特征选择方法研究较少，特别地，当数据集含有异常点时，现有的特征选择方法几乎都不能很好地选出有效特征.本文提出的面向异常点的稳健回归特征选择方法AWLASSO，通过自适应正则项自主更新损失函数权重，进而迭代估计回归系数.AWLASSO的迭代过程总是朝着较好的回归系数估计值方向进行，在迭代后期其训练集含有足够的样本，因而其获得了较好的实验结果.此外算法可以排除异常点的影响，故其能较好地同时完成特征选择和学习器训练.与经典的LASSO和LAD-LASSO相比，本文提出方法更稳健、更稀疏，即使异常点含量较多该方法依然有效.然而该方法中的正则参数λ对方法性能有一定影响，如何进一步提高方法的稳健性是我们未来的研究工作.