Heavy-Ball型动量方法的最优个体收敛速率

程禹嘉 陶 蔚 刘宇翔 陶 卿

1(中国人民解放军陆军炮兵防空兵学院信息工程系 合肥 230031)2(中国人民解放军陆军工程大学指挥控制工程学院 南京 210007)

机器学习问题普遍可以转化为求解目标函数最小值的优化问题，一阶梯度优化方法由于具有算法简单、迭代成本小等特点，成为处理大规模数据问题的首要选择.在此基础上发展起来的随机优化方法由于避免了每一次迭代都需要遍历整个样本集，充分利用训练样本集合的冗余性，从而具有计算代价低和实际收敛速率快等优点，已经成为处理大规模机器学习问题的实用方法[1].

动量方法是在经典梯度下降方法的基础上通过添加动量而获得的一种特殊的一阶优化方法.研究者将动量算法分为2类：一类是Polyak于1964年提出的Heavy-ball型动量方法[2],另一类是1983年Nesterov提出的NAG(Nesterov accelerated gradient)型动量方法[3].这2类算法的主要差别在于所使用动量项的不同，前者只是使用了前一步的迭代信息而后者引入了当前步迭代算法的二阶信息.对于不同条件下的优化问题，这2类算法的收敛性也有不同的表现.当目标函数光滑时，NAG具有最优的O(1/t2)收敛速率[3]，其中t为算法的迭代步数.当目标函数强凸且二次可微时，尽管Heavy-ball型动量方法、梯度下降法和NAG方法都具有相同的线性收敛速率，但Heavy-ball型动量方法具有最小的收敛因子[2].随机动量方法被广泛应用于神经网络的训练，并显著的提高了其收敛性能[4].

NAG是优化领域具有里程碑意义的算法，它填补了Nemirovski与Yudin所证明的“任何一阶优化算法都不可能得到比O(1/t2)更快的收敛速率[5]”的间隙，也吸引了众多机器学习研究者的关注.特别是针对大规模具有特定含义的正则化损失函数优化问题，研究工作层出不穷.早期重要的工作主要包括只要损失函数满足光滑性条件就可得到整个目标函数光滑时的最优收敛速率[6-7]，以及NAG随机形式的最优收敛速率等等[8].近期NAG的研究主要集中在与其他优化方法的结合上.如2015年Lin等人基于NAG提出了一种通用的加速策略Catalyst[9]，在目标函数强凸的条件下将批处理优化方法、坐标优化方法和增量优化算法进行了加速.最近，Allen-Zhu引入带有动量参数的方差项，提出了著名的Katyusha算法[10]，成功地将方差减少方法与NAG相结合.2018年Shang等人将NAG算法与Mixed Optimization算法相结合，仅使用了一个动量项就取得了与Katyusha算法相同的收敛速率[11-12].

与标准的梯度下降法相较，Heavy-ball型动量方法在目标函数在某些方向变化较弱而在另一些方向变化很强的时候，可以取得好的加速效果，复杂度却几乎没有增加.但与NAG方法相比，Heavy-ball型动量方法的研究却屈指可数.2014年Ghadimi等人对Heavy-ball方法的收敛性进行了深入的研究，给出了目标函数光滑条件下的平均和个体收敛速率[13]，但均未达到最优.2016年Yang等人建立了一种含有多种参数的算法框架，统一处理了梯度下降法、Heavy-ball方法以及NAG方法[14]，在该框架中设置不同的参数即可得到不同的优化算法.这种统一的算法对于非光滑优化问题在平均输出方式下具有最优的收敛速率.

本文的主要工作有3个方面：

1) 对于非光滑优化问题，证明了Heavy-ball型动量方法具有最优的个体收敛速率.据我们所知，这一结果填补了Heavy-ball型动量方法在非光滑情形下个体最优收敛性研究的缺失，有助于更全面地理解Heavy-ball型动量方法，也说明了在处理非光滑问题时Heavy-ball型动量方法和NAG具有同样的重要地位.

2) 本文证明基于光滑情形下Heavy-ball型动量方法的收敛性分析[13]，但不同的是，为得到非光滑情形下的个体最优收敛速率，我们巧妙构造了步长和动量权重的迭代方式，同时利用Zinkevich在处理在线优化方法收敛性使用的技巧[22]，避免了变步长和权重导致的递归问题.

3) 通过典型的稀疏优化问题实验，验证了理论分析的正确性以及所提算法在保持稀疏性方面的良好性能.

1 典型动量方法的收敛性介绍

本节我们对2种动量方法的收敛性以及它们之间的联系和区别进行必要的介绍.

考虑有约束优化问题:

(1)

其中，f(w)为凸函数，Q⊆Rn是有界闭凸集合，记w*为式(1)的一个最优解.批处理形式投影次梯度方法的迭代步骤为

(2)

Agarwal等人给出非光滑条件下式(2)的平均收敛速率为[25]

(3)

式(2)的个体收敛速率由Shamir和Zhang Tong证得[18]：

(4)

这与最优速率之间还是存在着数量级上的差距.

Yang等人建立了随机梯度下降法与随机动量方法的统一框架[14]：

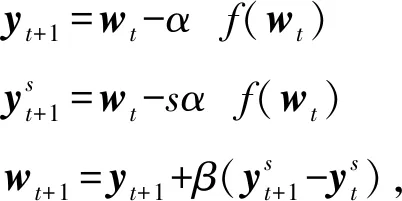
(5)

其中,β为动量参数，s≥0.随着s由大至小，式(5)依次变为

(6)

2) 当s=1时，即为NAG方法：

(7)

3) 当s=0时，即为Heavy-ball方法：

(8)

通过选取适当的步长，文献[14]给出了平均收敛速率：

(9)

在光滑目标函数条件下，由于NAG方法进行每一步迭代时都会使用之前迭代的部分甚至全部信息，所以通常可以取得较Heavy-ball方法更快的收敛速率.当目标函数光滑且强凸时，梯度下降方法、Heavy-ball方法与NAG均可以达到线性收敛，即：

f(wt)-f(w*)≤qt[f(w0)-f(w*)],

(10)

但Heavy-ball方法获得的收敛因子q是最小的[13].

文献[19]通过在投影次梯度上进行了线性插值的操作：

(11)

(12)

其中,θt与ηt为步长参数，与线性插值技巧不同的是该方法每一步的解都是通过投影直接得到，因此可以得到良好的稀疏效果.与之类似，Heavy-ball方法的个体解也应当具备稀疏性.

2 个体最优收敛性分析

本节给出Heavy-ball方法在目标函数非光滑条件下的个体收敛性证明.

(13)

从式(13)可以看出，Heavy-ball型动量方法是在梯度下降法基础上添加了动量项pt.正是由于与梯度下降法的这种相似性，使得梯度下降法的收敛分析思路也可以用于Heavy-ball方法.

值得注意的是，文献[13]将α和β均设定为常数，但对于非光滑优化问题，这样的选取办法无法获得个体收敛速率.因此我们选取了时变的α与β，但此时又会导致式(13)的迭代关系不成立.为了解决这个问题，我们设置pt=t(wt-wt-1)，通过巧妙地选取αt和βt(见定理1)，我们得到：

基于这个关系式，我们可以证明定理1.为了解决变步长和权重导致的递归问题，我们先证明引理1.

具体证明见附录1.

具体证明见附录2.

仅考虑二分类问题，假设训练样本集

S={(xi,yi)|i=1,2,…,m}⊆Rn×{+1,-1},

其中(xi,yi)是独立同分布的.

考虑非光滑稀疏学习问题的损失函数为“hinge损失”，即fi(w)=max{0,1-yiw,xi}的优化目标函数为

(14)

约束情况下随机形式的Heavy-ball算法的迭代步骤自然可以表示为

(15)

其中i为迭代到第t步时随机抽取的样本序号.

(16)

算法1.随机Heavy-ball算法.

输入: 循环次数t；

输出:wt.

① 初始化向量w1=0；

② Fork=1 tot

④ 随机选取i∈{1,2,…,m}；

⑥ 由式(15)计算wk+1；

⑦ End For

3 实 验

本节对算法1的个体收敛速率及其稀疏性的理论分析进行实验验证.

3.1 实验数据集和比较算法

实验所采用的6个常用标准数据集，分别为ijcnn1,covtype,a9a,CCAT,RCV1,astro-physic.数据集来源于LIBSVM网站[注]https:www.csie.ntu.edu.tw～cjlinlibsvm.表1给出了这6个数据集的详细描述.

Table 1 Introduction of Standard Datasets表1 标准数据集描述

实验采用5种随机优化方法进行比较，这些方法分别为平均形式输出的标准投影次梯度方法[25,27]、线性插值投影次梯度方法[19]、NAG方法[20]、平均形式输出的Heavy-ball方法[14]以及个体形式输出的Heavy-ball方法.从理论分析的角度来说，这5种随机优化方法的收敛速率均达到了最优.但在稀疏性方面，个体形式输出的Heavy-ball方法与NAG方法应该具有较好的表现，而平均形式输出的Heavy-ball方法、线性插值投影次梯度方法与标准的投影次梯度方法的稀疏性应该较差.

3.2 实验方法及结论

图1为5种算法的收敛速率对比图，其中纵坐标表示当前目标函数值与目标函数最优值之差.粉色实线与蓝色实线分别表示标准的投影次梯度方法与平均形式输出的Heavy-ball方法的收敛趋势，青绿色虚线与红色虚线表示线性插值投影次梯度方法与NAG方法的收敛趋势，绿色虚线则表示本文提出的以个体形式输出的Heavy-ball方法的收敛趋势.从图1可以看出，5种算法在6个标准数据集上运行了约5 000步之后，基本都达到10-2的精度，可以说均表现出基本相同的收敛趋势，这与理论分析的结果是吻合的.

图2给出了5种算法在6个标准数据集上的稀疏性对比，纵坐标表示各算法对应输出方式的稀疏度.稀疏性通过稀疏度来衡量，稀疏度是指变量中非零向量所占的百分比，所以稀疏度越高则稀疏性越差.从图2可以看出，线性插值投影次梯度方法虽然以个体形式输出，但稀疏性较差.而Heavy-ball方法与NAG方法个体解的稀疏度近乎相同，且都明显低于以平均形式输出的投影次梯度方法及Heavy-ball方法.由此可知，Heavy-ball方法的个体输出较好的保留了个体收敛在稀疏性上独具的优势.

另外，从图2中还可以看出，对于维数较低的前3个数据库，个体解的稀疏性明显优于平均解，基本接近数据集的稀疏度(见表1所示)，这充分说明个体解比平均解能更好地描述样本集的稀疏性.但个体解的稀疏度却存在着震荡现象，这主要是由于算法的随机性和稀疏度的分母较小导致的.对维数较高的后3个数据集，个体解同样可以描述数据集的稀疏度，但稀疏度已经不再震荡，与平均解一样平稳.

Fig. 1 Comparison of convergence rate图1 收敛速率比较图

4 结 论

与其他优化方法相比，Heavy-ball型动量优化方法目前所知的主要优势是在目标函数强凸且二次可微的条件下获得的收敛速率是最快的.本文对非光滑条件下Heavy-ball型动量优化方法的收敛性进行了初步的研究，证明了这种方法可以获得最优的个体收敛速率.众所周知，在不改变算法的情况下，梯度下降方法目前最好的个体收敛速率是Shamir和Zhang得到的与最优收敛速率差一个log因子的个体收敛速率[18].显然，本文的结论表明Heavy-ball型动量技巧是对梯度下降法个体收敛速率的一种加速策略，并且与NAG方法具有相同的性能.下一步我们将考虑Heavy-ball型动量优化方法在正则化和强凸条件下的最优个体收敛速率问题，我们还会考虑在随机Heavy-ball型动量优化方法中引进方差减少技巧进一步提升实际收敛效果.