基于逐步回归算法的边坡爆破振动控制研究
2019-07-29
(1.兰州理工大学 石油化工学院,兰州 730050;2.浙江大学 海洋学院,浙江 舟山 316021; 3. 福建省特种设备检验研究院,福州 350008)
1 研究背景
爆破振动控制是工程爆破研究的主要课题之一,合理的振动幅值能改善爆破效果、降低成本、确保周围建筑物安全、提高工程质量[1-2]。国内外学者对于爆破振动幅值研究大致有4种方法:萨道夫斯基法、数值法、波动法和数据拟合法[3]。卢文波等[4]、Tripathy等[5]、李启月等[6]、张立国等[7]采用多元回归法对实测数据进行回归拟合,确定不同影响因素下萨道夫斯基参数取值;胡建华等[8]利用数值法的相似理论,推导出修正后的爆破振动速率公式,分析不同影响因子和振动速率之间的变化关系以及因子之间的相关性;Dhakal等[9]亦采用文献[8]的方法研究了爆破振动引起的结构响应特性;李夕兵等[10]、杨建华等[11]、谢全民等[12]采用波动法对爆破振动速率进行研究,将垂直方向爆破速率峰值作为振动大小的判据;徐全军等[13]、文建华等[14]采用遗传算法或神经网络算法对现场实测爆破振动数据进行拟合分析,使得实测值与预测值之间存在较高拟合度,该方法可较准确地给出适合具体施工现场的振动峰值速度模型,但未考虑变量因子之间的相互影响。
本文采用萨道夫斯基和数据拟合相结合的方法,实施修正后的多元回归拟合。振动速率回归分析前将振动速率影响因子函数化,对因子函数逐步回归分析,确保最终入选因子的优越性;再将实测振动数据进行逐步回归,剔除不显著因子,入选显著因子,确定道夫斯基公式参数。该算法优点在于不仅可以分析自变量和因变量之间的影响关系,还可以分析自变量之间的相互影响程度,保证了因子的全面性、完整性和初始性,并且代入运算的因子都经过了循环筛选,显著性较高;所以修正后的多元回归拟合用于爆破振动研究更具有优越性。吕涛等[3]在对萨道夫斯基公式研究过程中忽略高程和主频的影响,而通过相关研究[15-17]发现,高程和主频大范围的变化会引起振动速率的发散。故对于爆破振动幅值研究,高程差和主频可视为主要的研究物理量。
2 逐步回归分析
逐步回归分析法主旨为自变量依次进入模型,每一个自变量因子进入模型都进行F检验,同时将已进入的自变量因子进行t检验;后引入自变量使前一引入自变量变得不再显著时,则将前一自变量剔除,每次循环后保留的自变量都对因变量有显著影响[18]。
2.1 基本原理
逐步回归类同于多元回归,假设有n组自变量和对应的应变量为
(1)
式中:xij表示第i组第j个自变量;yi表示第i组自变量对应的因变量。
多元回归方程求解过程中,可将多元回归方程的法方程改写为
(2)
式中:aij为法方程自变量;bj为未知量参数;Sj为法方程因变量;cij为变换参数。
(3)
直到m步(1≤m≤k),等价于方程两端各乘以一转换矩阵,即Dk[aij]{bj}=Dk[cij]{sjy};故此,向量[aij]的第2列被单位矩阵[δij]相应置换,其他元素也进行了相应变换。同时,向量[Cij]相应单位列向量被另一个列向量(式(4))所置换,其余各元素向量也进行了等价变换。
(4)
随着循环计算的进行,部分预报因子xm被选入回归方程,同时单位向量已经置换成相应[aij]中被选入因子xm对应的各列,新向量也引入了[cij]对应的各列中。
2.2 基本步骤
2.2.1 计算相关矩阵
为保证计算的精度与准确性,将一次均值算法换为二次均值算法,用标准化的相关矩阵[rij]代替[sij],扩展为(k+1)阶矩阵,y用n表示,即
(5)
其中:
式中:xi为研究对象的自变量;yi为研究对象的因变量,故有
(7)
2.2.2 因子的筛选和消元变换
由以上循环计算后,第m步回归循环时回归方程各引入和剔除变量所用特征值可表示如下。
(9)
其中,
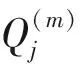
(2)剩余平方和Q(m),其表达式为
(11)
(12)
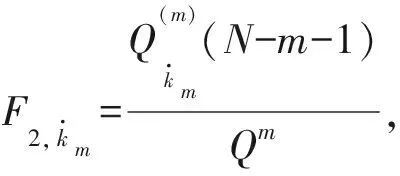
(4)引入因子xkm+1的检验。在第m步循环时,偏回归平方和最大的因子对应变量y影响最为显著,故选入回归方程,即
(13)
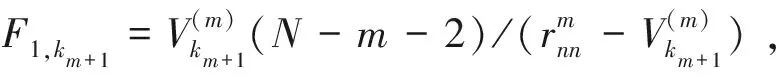
2.2.3 回归方程
进行第m步循环时,回归方程为
(14)

图1 试验现场及测振仪安装Fig.1 Blasting circumstance and vibration instrument
3 工程实例
某施工平台临近高陡边坡,紧接最终边坡的交接位置,岩层较为破碎,因前期爆破振动影响,台阶稳定性较差。为了保证安全生产、确保最终边坡的稳固以及提高生产效益和经济利益,现对爆破振动信号幅值传播规律进行研究。起爆药包为海西东诺产Φ32 mm乳化炸药,干孔炸药采用海西东诺产岩石膨化硝铵炸药,水孔采用Φ90 mm水胶炸药;5次不同时期爆破施工过程对爆区周围地表质点采用爆破测振仪进行测振试验,每次试验安装4个临近监测点,共计20组试验数据;但因为各种操作和接收原因,部分测振结果数据杂散,无法使用,故只有18组数据可用于研究分析。试验现场及测振仪安装见图1。
4 基于逐步回归分析的振动速率监控
4.1 炸药量逐步回归分析
1978年兰格福尔斯在《岩石爆破现代技术》中给出了有关爆破药量计算的半经验公式[19],即
Q=k2W2+k3W3+k4W4。
(15)
式中:Q为爆破药量;W表示最小抵抗线;W2表示与介质破裂面积相关的参量;W3表示与介质体积相关的参量;W4表示与最小抵抗线相关的参量,又称之为“膨胀”或“抛掷”分量;k2,k3,k4均为系数。
此次爆破测振试验炸药量以及相关参数取值如表1所示。
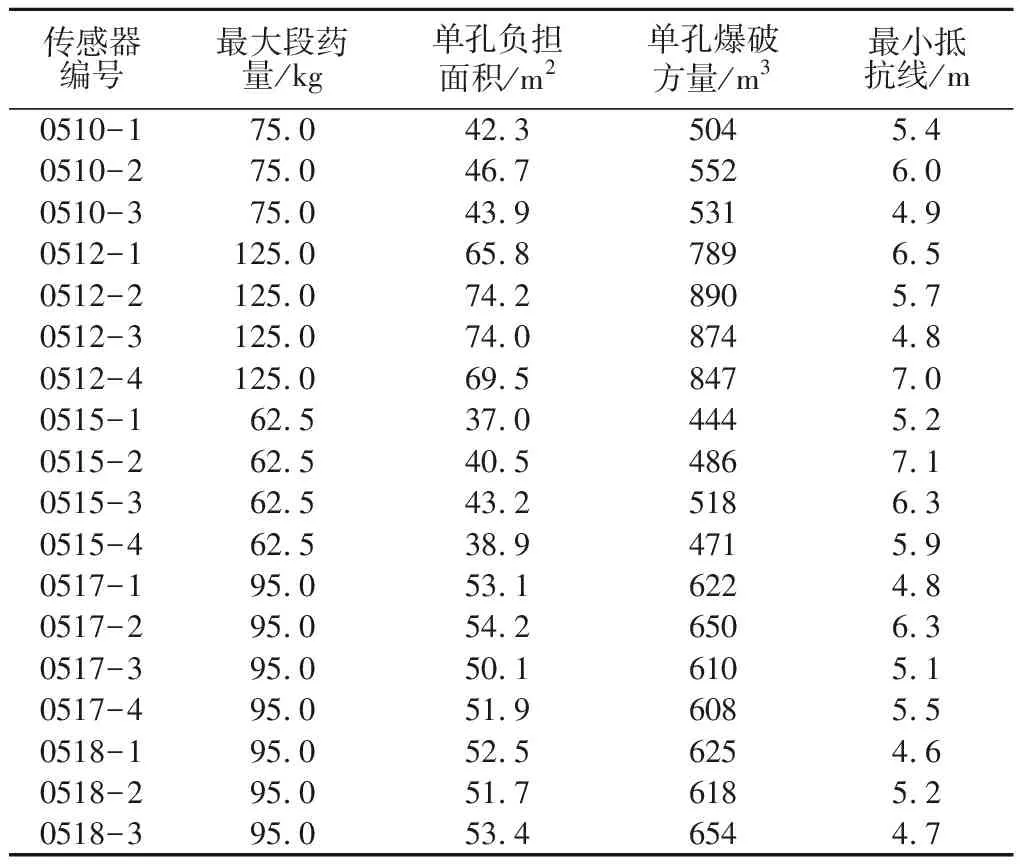
表1 炸药量相关参数Table 1 Parameters of explosive charge
注:0510-1表示5月10日测量时编号为1的传感器,以此类推
单孔负担面积、单孔爆破方量、最小抵抗线等诸多因素直接影响炸药量的取值,并且这些因素之间也存在着不同程度的影响,要在一个函数模型里考虑到所有影响因素不太现实。因此,采用灰色关联理论建立相关函数模型分析各因子之间的关联程度。本文采用逐步回归的理念,入选显著影响因子,剔除不显著影响因子,通过逐步回归循环达到最优取值的目的。
建立逐步回归模型,程序运行后得到:k2=0.057,k3=0.359,k4=0.084,常值为-0.017;依据逐步回归入选与剔除原理,得到选入因子为单孔爆破方量,剔除因子为单孔负担面积和最小抵抗线。对回归报告进一步分析,可知回归方程中R2=0.940,F=248.816;方程确定性系数R2表示自变量对因变量的相关性,其取值在[0,1]之间,越靠近1,表明相关性越强;回归方程的线性关系显著性由F的显著性来检验,查F(3,14)分布表得λ=6.68,F=248.816>λ,由于Sig=P(F>λ)=0<0.05(置信水平),表明该回归方程相关性特别显著。
对炸药量函数进行逐步回归分析时,因变量(炸药量)与自变量(单孔负担面积、单孔爆破方量)之间的数据分布如图2所示,该图可以直观显示除部分野值点外的相对合理准确数据的变化趋势。
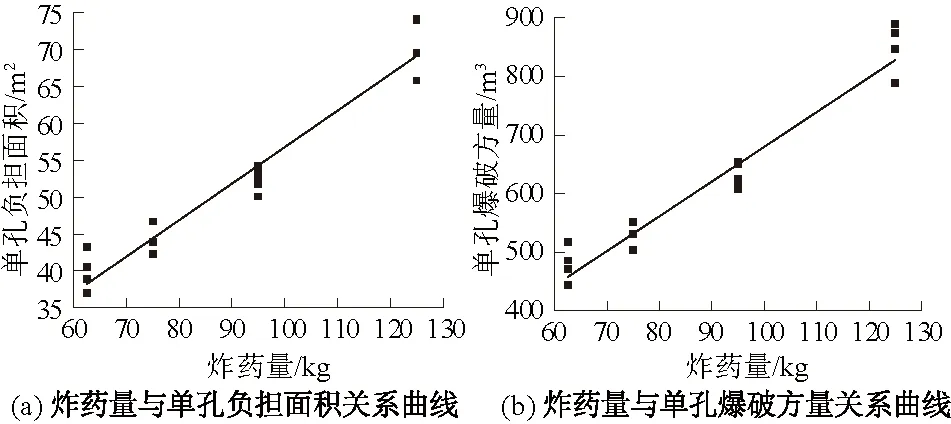
图2 炸药量与单孔负担面积、单孔爆破方量之间的关系曲线Fig.2 Curves of explosive charge vs. burden area ofsingle-hole and unit volume of single-hole blasting
经逐步回归分析后炸药量函数关系可表示为
(16)
工程爆破实例中,一般最小抵抗线W取值在0.5~10 m范围内。故在W=0.5~10 m范围,按照0.5 m的步长取20个值代入上式进行运算。最终结果表明:当W>2 m时,介质破裂面积相关参量(公式第1项)与总药量的比值<10%;当W<10 m时,最小抵抗线相关分量(公式第3项)与总药量的比值<10%;按照《爆破安全规程》规定,爆破允许误差为±10%以内,则当2 m≤W≤10 m时爆破炸药量主要由爆破方量所决定,此时炸药量公式可改写为
Q=k3W3。
(17)
4.2 振动速率逐步回归分析
在该爆区进行5次爆破测振试验,共采集18个点次的振动速率相关数据,具体如表2所示。采集0510-1所测的垂向振动速率传播规律,如图3所示。
国内外对于爆破振动峰值速率模型运用最为广泛的是萨道夫斯基公式[20-21],具体数学模型如式(18)所示。
(18)
式中:V为质点垂直方向的最大振动速率;R为水平距离;k,α均为与爆区环境中水文地质、地形条件以及介质参数等相关系数。
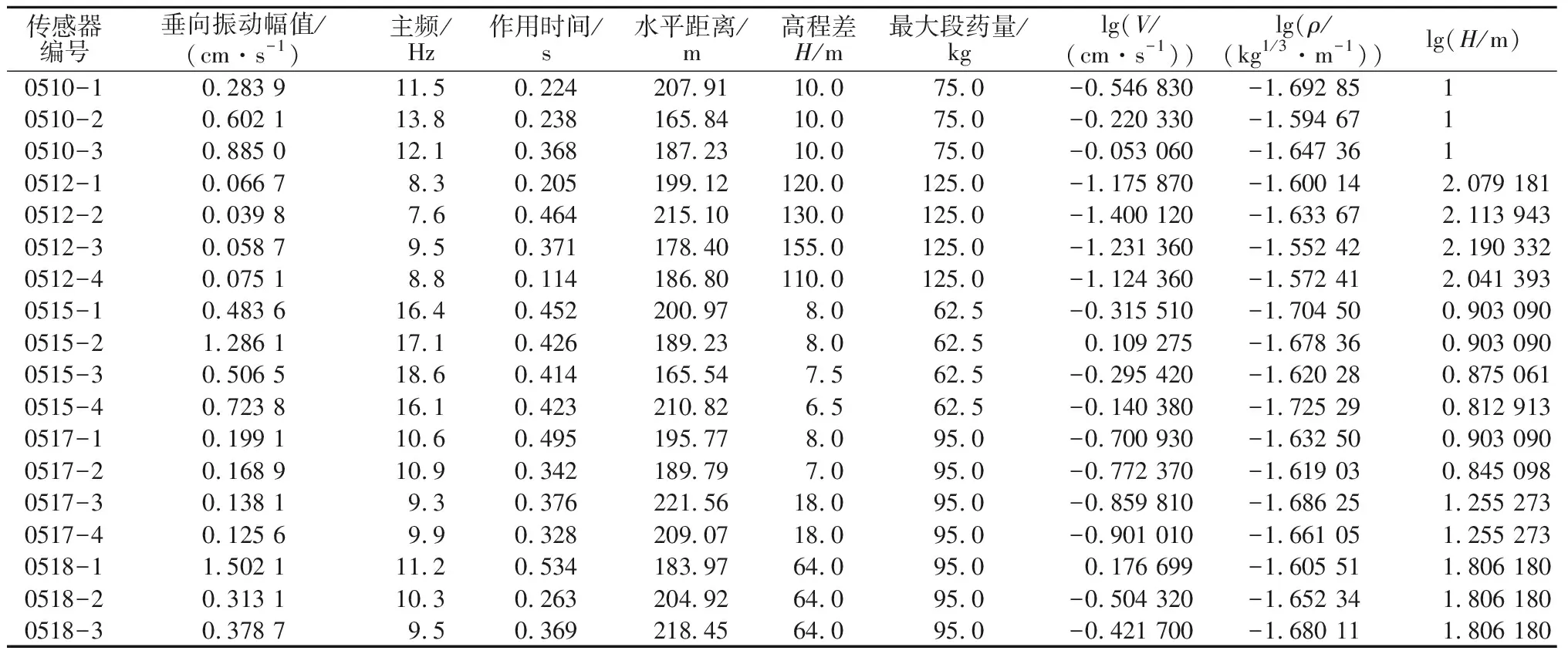
表2 试验爆区振动数据Table 2 Vibration data of blasting area
注:ρ为比药量
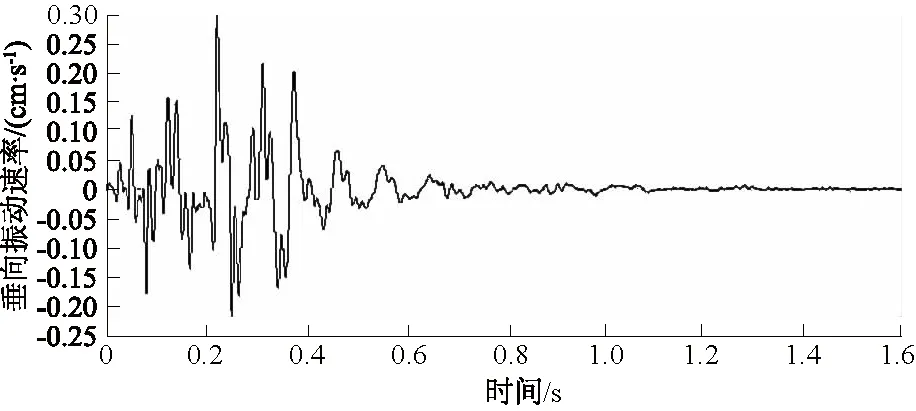
图3 垂向振动速率-时间分布规律Fig.3 Distribution rule of vibration velocityin Y axis against time
实践表明,高程对于振动速率具有重要影响,当高程超过一定值时爆破振动信号会出现高程放大效应[22-23]。为研究高程对爆破振动信号影响规律,本文对含高程参量的萨道夫斯基公式进行逐步回归分析,具体函数方程为
(19)
式中β为与爆区环境中水文地质、地形条件以及介质参数等相关的系数。
lgV=lgk+αlgρ+βlgH。
(20)
建立逐步回归模型,程序运行后得到:k=200.8,α=1.8,β=-0.563;对回归报告进一步分析,可知回归方程中方程确定性系数R2=0.973,基本接近1,表明自变量对因变量有较强的相关性,该回归方程相关性特别显著。经逐步回归后可得振动速率函数关系为
(21)
4.3 高程放大影响
边坡爆破振动速度的高程放大效应是在一定条件下产生的,受爆破振动荷载特性及边坡坡形和坡高等因素的影响。爆破振动荷载作用下,边坡坡面不同高程台阶岩体结构的自振主频处于爆破振动荷载主频带范围内,台阶部位岩体结构的振动响应会产生“鞭梢效应”。大量工程实例验证表明,运用萨道夫斯基公式预测地表质点峰值振动速度时,只有在同一高程的平整地形下具有较高精度,如存在较大高程差以及地表起伏明显的情况下,实测数据与预测数据之间存在较大误差。故国内外部分学者[22-23]对高程影响振动峰值速度进行研究,并指出超出一定范围时随高差正向增大高程放大率也出现增大效应,反之降低。
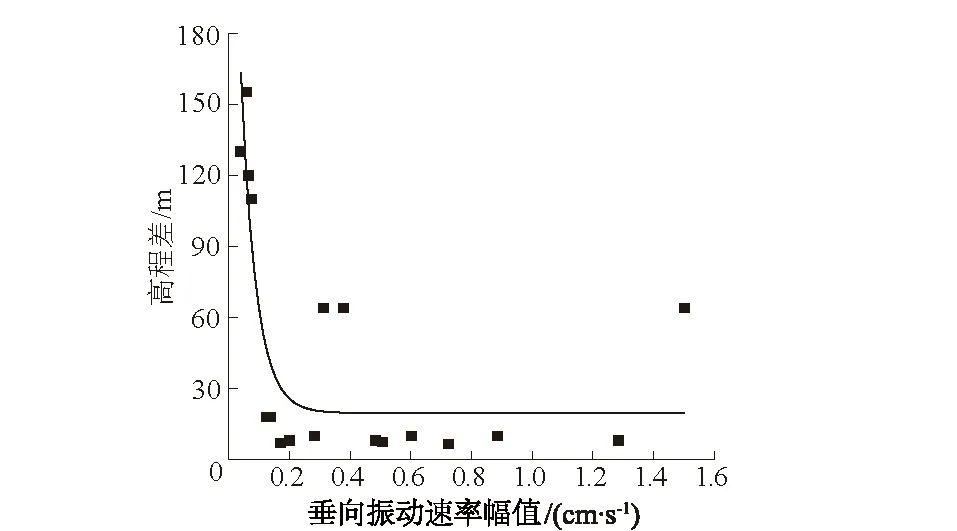
图4 垂向振动速率幅值-高程差变化曲线Fig.4 Variation of vibration amplitude in Y axisagainst elevation difference
垂向振动速率幅值-高程差变化曲线如图4所示。由爆区垂向振动速率逐步回归分析报告和图4可知:高程差作为入选因子进入回归方程,而比药量在循环过程中逐步被剔除。除去部分野值点外,越靠近炮孔,振动速度越大;随监测点离炮孔距离增大,地表质点振动速率呈递减趋势。
根据此次爆破测振试验数据可确定与该爆区环境中水文地质、地形条件以及介质参数等相关系数k,α,β的取值,且已知每次起爆的最大段药量Q;将这些参数代入式(17)可得到不考虑高程影响的爆破振动峰值速度V。
假设高程放大率为ε,则高程放大率公式可表示为
ε=(Hv-Pv)/Pv。
(22)
式中:Hv为考虑高程影响时的最大垂向速度;Pv为不考虑高程影响时的最大垂向速度。
通过对高程放大率和高程差回归分析可确定边坡爆破高程放大效应的临界值。当ε>0时,会出现爆破振动信号放大效应;针对本文所研究的施工环境、地质条件和爆破参数,对放大率和高程差回归分析可得ε=1.693H-63.7;故依据理论分析给出的高程放大率公式可确定该施工条件下当高程差超过38 m时,出现明显的振动信号放大效应。
图5为高程差-高程放大率变化曲线,通过分析图5可以看出:抛去部分野值点外,在本文监测范围内,当高程差超过38 m时,随高程差值增大,高程放大率也呈现出显著增强趋势。
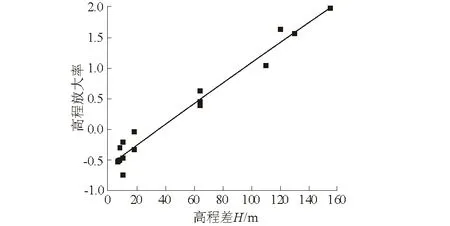
图5 高程差-高程放大率变化曲线Fig.5 Curve of elevation difference vs. elevationamplification
4.4 主频预测公式的回归分析
此次测振试验中采集0510-1时所测得的垂向振动速率幅值-主频变化规律,如图6所示。
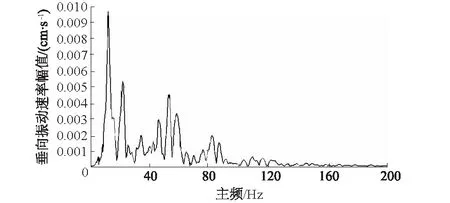
图6 垂向振动速率幅值-主频变化规律Fig.6 Distribution rule of dominant vibrationfrequency vs. vibration velocity in Y axis
在爆破振动频率采集过程中,通常选取最大振幅所对应的频率(主频f)为研究对象,原因是爆破振动频率特性很大程度是由主频所决定的。由爆破振动频率相似准数方程可预测工程爆破中任意一介质点的振动主频函数模型为[4]
(23)
取测振试验采样的18个测点y轴方向(垂直)的主频-速度相关数据,对主频函数模型进行逐步回归计算,求得k=231.4,α=-0.76,R2=0.940,F=456.19,Sig=0.03;方程的确定性系数R2基本接近1,线性关系显著性F=456.19>λ,Sig=P(F>λ)=0.03<0.05(置信水平),说明此次逐步回归运算中,主频回归方程特别显著,故主频预测函数关系式可表示为
(24)
主频与比药量的线性回归结果和主频与Q,R的关系曲线分别如图7、图8所示。分析图7、图8可知:比药量ρ为定值时,随水平距离R的增大,主频呈递减趋势;炸药量Q不变时,随水平距离R的增大,主频呈递减趋势,并且递减速率逐渐变缓;水平距离R不变时,随炸药量Q的增大,主频呈递减趋势,并且递减速率逐渐变缓。
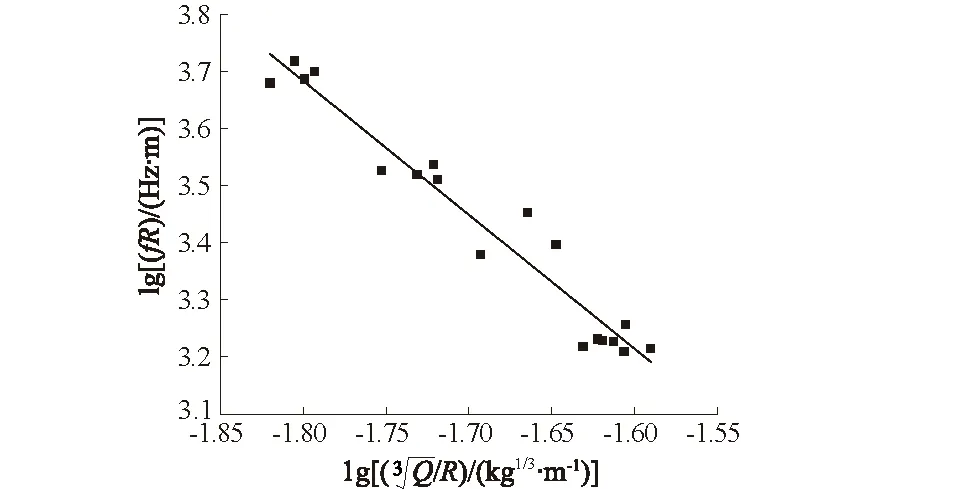
图7 主频与比药量的线性回归结果Fig.7 Linear regression relationship between dominantfrequency and specific charge
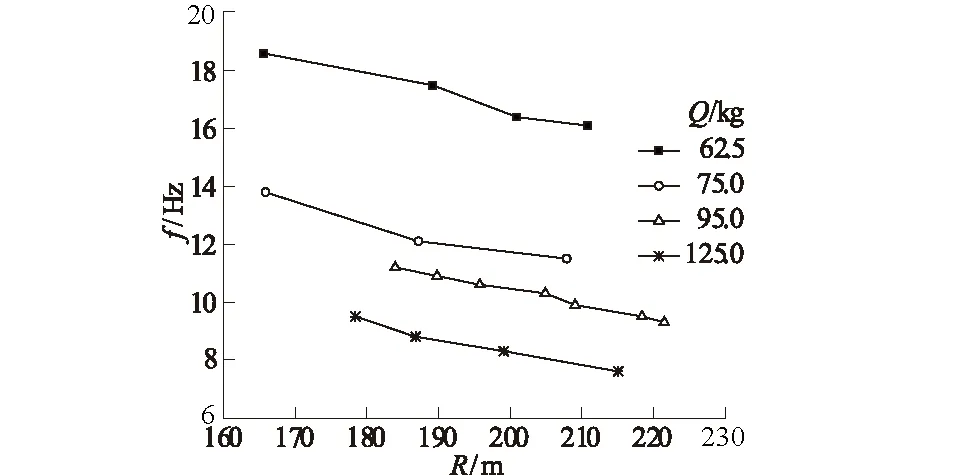
图8 主频与Q,R的关系曲线Fig.8 Curves of dominant frequency against Q and R
5 结 论
(1)对于爆破振动幅值这种多预报因子影响的函数研究,可采用改进的多元回归分析模型,即转换为逐步回归分析,这样就可以剔除不显著预报因子,避免了全部因子进入回归方程,导致无法计算或者降低了计算精度。
(2)通过对炸药量函数逐步回归分析发现:当最小抵抗线W>2.0 m时,炸药量主要由单孔爆破方量决定;随单孔药量的增加,单孔负担面积、单孔爆破方量都呈线性递增趋势。
(3)对高程差与高程放大率函数回归分析发现:当高程差超过一定范围时,爆破振动信号才会出现高程放大效应;由高程放大率函数可求得针对此次爆破施工条件出现高程放大效应的临界差值为38 m左右;随高程差值继续增大,振动信号放大率也逐步增强,在本文监测范围内高程差取值越大,振动信号放大作用越强。
(4)主频函数逐步回归分析结果表明:比药量ρ为定值时,随水平距离R增大,主频呈递减趋势;炸药量Q为定值时,随水平距离R增大,主频呈递减趋势,并且递减速率逐渐变缓;水平距离R为定值时,随炸药量Q的增大,主频呈递减趋势,并且递减速率逐渐变缓。
