基于GACO-BP-MC的大坝变形监控模型
2019-07-29董丹丹祖安君孙雪莲
董丹丹,祖安君,孙雪莲
(1.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098; 2.河海大学 水利水电学院,南京 210098)
1 研究背景
大坝安全监测资料是大坝运行性态的直接反映,其中变形监测量承载了荷载和环境作用下坝体安全性能演化的丰富信息,在国内外已普遍作为大坝最主要的效应监测量。因此通过建立相应的安全监控模型来对大坝变形性态进行评价和预测,对馈控结构安全状态和保障大坝稳定运行非常重要[1-2]。目前,应用较广泛的大坝变形监控模型主要有统计模型、确定性模型和混合模型3种常规模型以及组合模型、人工智能分析模型等。总体来说,大坝变形监控模型大致有由常规模型向组合化、智能化方向发展的趋势[3-4],模型精度也逐渐得到了提高。
计算机技术如今发展十分迅速,很多人工智能算法被应用于大坝变形监控和预测方面,其中BP(Back Propagation)神经网络是近年来被普遍应用的一种多层前馈神经网络,利用误差反向传播的学习算法,具有复杂的非线性映射能力,能准确描述输入值与输出目标之间的映射关系。针对BP神经网络训练时间长、收敛慢、易陷入局部极小值的缺点[5],目前也采用了许多算法对其进行优化,如遗传算法(Genetic Algorithm,GA)、蜂群算法、蚁群算法(Ant Colony Optimization,ACO)等。其中,采用蚁群算法训练BP神经网络的初始权值和阈值,可以有效加快收敛速度且可避免陷入局部极小值。已有牛景太等[6]将蚁群算法用于BP神经网络的优化,建立了监控混凝土坝位移的ACO-BP模型,并通过实例验证了所建模型的可行性和有效性,但蚁群算法也存在因寻优初期搜索完全随机缺乏指导导致的收敛速度慢的问题[7]。为此,本文引入遗传算法来改进蚁群算法,结合2种算法共同来优化BP神经网络的参数,充分发挥遗传算法的快速全局搜索能力和蚁群算法的正反馈优势,从而加快蚁群算法收敛速度并避免陷入局部最优点;另外,马尔科夫链(Markov Chain,MC)适合于随机波动性较大的时间序列的预测,能够较好地反映受多种因素影响产生的随机性能[8]。故为了提高预测的精度,本文在利用遗传算法改进的ACO-BP模型进行预测的基础上,结合MC模型对预测值与实测值之间的残差进行修正,建立基于GACO-BP-MC的大坝变形监控模型,并通过实测数据来验证所建模型的拟合与预测能力。
2 基于GACO-BP-MC的大坝变形监控模型的构建
2.1 蚁群神经网络(ACO-BP)模型
BP神经网络包含输入层、隐含层和输出层3部分,使用梯度下降法进行训练,在非线性拟合和预测方面应用广泛;蚁群算法是仿照自然界蚁群觅食行为的一种生物启发式算法,具有分布、并行和全局收敛的能力,用它来对神经网络的权值和阈值进行训练,可有效改善BP神经网络的训练性能。BP神经网络和蚁群算法的基本原理可参考文献[7],在此不再赘述。
ACO-BP模型的基本思想是:假设神经网络有n个待优化参数(即全部权值和阈值),每个参数pi(1≤i≤n)的取值区间为(Wmin,Wmax)。将每个参数的取值区间等分为s个子区间,在每个子区间相应的取值范围内随机取一个候选值,这s个子区间形成子区间集合Ipi,给集合中每个元素均分配相应的信息素浓度。每只蚂蚁根据集合中每个元素的信息素浓度计算相应概率,依次从集合Ipi(1≤i≤n)中选择一个元素即一个子区间,直至选定所有集合中的元素,它便选取了一组BP神经网络的参数组合,然后按照相应规则调整集合中子区间对应的信息素浓度。蚂蚁搜索时,只通过信息素进行通信,不同的蚂蚁选择元素是相互独立的。重复上述过程,由于蚁群算法的正反馈性,蚁群将逐渐收敛到最优解上。蚁群算法优化BP神经网络参数的步骤如下:
(1)建立一个3层BP神经网络,则蚁群算法待优化参数pi的个数为n=(R+1)S1+(S1+1)S2,其中R,S1,S2分别为BP神经网络输入层、隐含层、输出层的节点个数。
(2)初始化蚁群算法的参数,令迭代次数NC=0,设置最大迭代次数为NCmax,设置集合Ipi(1≤i≤n)中所有元素的初始信息素浓度相等,即τij(0)=c(i=1,2,…,n,j=1,2,…,s),全部蚂蚁在蚁巢就绪。
(3)启动所有蚂蚁,每只蚂蚁按式(1)计算的概率通过轮盘转法逐个从每个参数的子区间集合Ipi(i=1,2,…,n)中随机选取一个元素,直至蚁群全部选定所有参数的子区间。
(1)
式中:Pij(t)为t时刻集合Ipi中第j个元素被蚂蚁选择的概率;τij(t)表示t时刻集合Ipi中第j个元素的信息素。
(4)令NC=NC+1;每只蚂蚁选择的n个元素均对应一组BP神经网络的权值组合,将其作为神经网络初始权值和阈值并计算相应的输出误差,记录当前的最优解。重新设置全部蚂蚁,再按照式(2)更新各个参数的子区间集合中元素对应的信息素浓度。
τij(t+1)=(1-ρ)τij(t)+Δτij。
(2)
式中:ρ为信息素挥发系数;Δτij为信息素增量,由式(3)计算得到,即
(3)
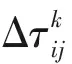
(4)
式中:Q为信息素常量;ek表示第k只蚂蚁选取的一组权值作为神经网络的初始权值时实际输出值与期望输出值之间的均方根误差,可由式(5)计算,即
(5)
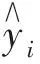
(5)重复步骤(3)—步骤(4),直到迭代次数NC≥NCmax或蚁群全部收敛到同一组参数组合,则输出当前发现的最优解,并将其赋值给BP神经网络的初始权阈值进行训练,循环结束。
2.2 遗传算法改进的蚁群神经网络(GACO-BP)模型
蚁群算法通过信息素的积累和更新而逐渐收敛于最优路径,具有全局收敛的能力,但是由于搜索初期算法初始值设置缺乏指导的原因,只能将每个集合的元素均设置相等的初始信息素浓度,导致寻优初期蚂蚁充满盲目性地随机搜索,朝向最优解路径收敛速度缓慢,计算时间长。
遗传算法是一种进化算法[9],具有全局随机搜索能力,它是以生物界中“物竞天择、适者生存”的演化法则为基本原理,将问题参数编码为染色体,再通过不断地选择、交叉及变异等运算来交换种群中染色体的信息,最终生成符合优化目标的染色体。而单独用遗传算法来训练BP神经网络时,因遗传算法对系统中的反馈信息利用不到位,所以导致求解效率低。
针对以上问题,本文结合2种算法共同来优化神经网络的参数,因遗传算法具有快速随机的全局搜索能力,故利用遗传算法来改进蚁群算法。先通过遗传算法寻优产生问题的初始解来指导生成蚁群算法初始信息素分布,然后借助蚁群算法的正反馈性寻求最优解,最后将最优解作为初始权值训练神经网络得到最终结果。结合2种算法的优点[10],既能缩短算法寻优初期的搜索时间以加快收敛速度,又能避免陷入局部最优而提高求解效率。遗传算法改进蚁群神经网络算法的步骤如下:
(1)初始化遗传算法参数,遗传算法需优化的参数pi的个数为n(参数定义同2.1节,染色体采用实数编码方式,将这些参数构造成染色体并进行编码,生成相应的染色体种群。
(2)用BP神经网络实际输出值与期望输出值之间的均方根误差E来衡量神经网络的性能,即
(6)
式(6)中符号意义同式(5),均方根误差越小表示神经网络的逼近收敛性能越好。
本文的适应度函数为
(7)
式(7)表示均方根误差越小的个体,适应度值越大,个体越优。
(3)采用轮盘赌法和最优保存策略相结合的方法来进行染色体个体选择,以完成染色体种群的筛选,保留适应度较大的个体。计算种群中全部个体的适应度,则个体i被选中的概率为
(8)
式中:fi(i=1,2,…,d)表示个体的适应度值;d为种群规模。
(4)从种群中随机选择2个个体进行染色体交叉操作,从而产生2个新的个体。因个体采用实数编码,所以采取实数交叉法。第k个染色体xk和第l个染色体xl在第j位的交叉方法为
(9)
式中b为[0,1]区间的随机数。
(5)变异操作从种群中随机选择一个个体,选择个体的一点进行变异,第i个染色体的第j个基因进行变异,其操作方法为
(11)
式中:r和r2均为[0,1]区间内的随机数;g为当前进化代数;Gmax为最大进化代数;xmax与xmin分别表示基因xij的上界和下界。
(6)当选择、交叉和变异操作完成后,则产生新一代染色体种群矩阵,此时应用最优保存策略来将最优个体保留到下一代染色体种群中。具体操作方法为:如果有新的个体适应度比当前最佳的个体适应度大,则该个体成为新的当前最佳个体;否则,用当前最佳个体取代新种群中最差的个体。
(7)重复上述步骤,直至遗传算法循环结束条件得到满足,即遗传代数达到最大遗传代数,则循环结束。
(8)迭代结束后,利用遗传算法的求解结果对蚁群算法的初始信息素分布进行指导。首先将每个神经网络参数pi(1≤i≤n)的取值区间等分为s个子区间,构成子区间集合Ipi,并对所有子区间设置相等的初始信息素,然后选取染色体种群中适应度最好的前10%的优秀染色体个体作为优化解集合[11],通过解码得到一系列BP神经网络的权值组合,分别找到其对应的子区间,按式(12)改进蚁群算法中各个子区间的初始信息素分布。
(12)
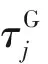
(9)继续利用蚁群算法对BP神经网络进行参数寻优,在参数pi(1≤i≤n)的各个子区间相应的取值范围内随机取一个候选值,对应的初始信息素分布由上一步确定,然后依照2.1节中步骤(3)—步骤(5)进一步搜索问题最优解。
2.3 MC残差修正模型
马尔科夫链是时间和状态均离散的马尔科夫随机过程[12],通过描述事件的发展规律来对未来状态进行预测,其预测模型的基本原理是根据系统现在所处的状态,通过状态转移概率矩阵得到系统未来可能达到某种状态的概率,不受过去状态的影响,适用于随机波动性较大和受多种因素影响的时间序列的数学处理,因此对于处理大坝安全监测数据具有一定的优势。
本文在由GACO-BP模型拟合并预测大坝变形规律的基础上,利用马尔科夫链分析实测值与拟合值的相对误差的波动规律,以此修正预测值并减小误差。具体步骤如下:
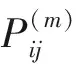
(13)
式中:Mi为相对误差序列中状态Si出现的次数,统计时因未来发展状态未知,故应去掉最后m个数据;Mij(m)为状态Si经m步转为Sj的次数。得到m步状态转移概率矩阵P(m)为
(14)
若起始状态Si的初始向量为P0,则经m步转移后的状态向量为
Pm=P0P(m) 。
(15)
(2)从序列中取距预测值最近N个已知状态的数值,由状态转移矩阵分别得到第i(i=1,2,…,N)个已知状态经m(m=N,N-1,…,1;m+i=N+1)步转移到预测值状态的概率,然后计算对应同一状态的N个概率值之和,取概率和最大者对应的状态为预测值相对误差的状态。
(3)已知GACO-BP模型预测值的相对误差的变化区间,取该区间的中点作为预测值的相对误差,则通过式(16)来修正预测值,即
(16)
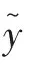
(4)对后续变形值进行预测,将前一个预测值加入原序列中并去除原序列中的第一个数据,构成新的样本序列,照此继续进行预测。
2.4 基于GACO-BP-MC的监控模型流程
采用GACO-BP-MC模型对大坝变形值进行预测的流程如图1所示。

图1 GACO-BP-MC模型流程Fig.1 Flow chart of GACO-BP-MC model
2.5 基于GACO-BP-MC的大坝变形监控模型输入和输出向量的确定
BP神经网络由输入层、隐含层和输出层3部分组成,取隐含层为1层,由此建立一个3层BP神经网络。本文GACO-BP-MC模型中BP神经网络输入层的节点数由大坝变形影响因子的个数确定,隐含层的节点数取为2x+1个(x为输入层节点数),输出层节点数则根据因变量个数确定。
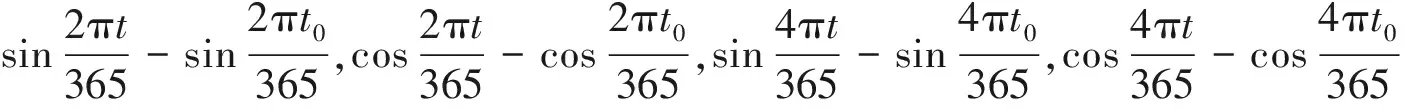
另外,进行神经网络训练时,由于各个变量具有不同的量纲和量级,为加快学习的速度,对训练样本数据按式(17)进行归一化处理。
X′=0.1+0.8(X-Xmin)/(Xmax-Xmin) 。(17)
式中Xmax,Xmin分别为因子变量的最大值和最小值。
3 工程实例
某水电站位于云南省大理州南涧县与临沧市凤庆县交界的澜沧江中游河段,大坝为混凝土双曲拱坝,坝高292 m,坝顶高程1 245 m,坝顶长922.74 m。水库正常蓄水位1 240 m,总库容约150亿m3,调节库容近100亿m3,具有多年调节能力。该水电站以发电为主,兼有防洪、灌溉、拦沙及航运等效益。
3.1 GACO-BP模型拟合和预测大坝变形
该水电站设置正垂线监测大坝变形,选取大坝22#河床坝段1 010 m高程的C4-A22-PL-05测点2012年2月15日—2014年5月15日的径向位移监测资料对所建模型的拟合效果和预测精度进行测试,每隔4 d取一组数据,共206组数据,前200组数据用于训练 GACO-BP模型检验拟合效果,后6组数据用于验证模型的预测精度。
GACO-BP模型的输入和输出向量按2.5节方法确定,初始化模型参数如下:BP神经网络参数pi的取值范围为-30~30,每个参数子区间划分数量s=60,每个子区间长度为1,最大训练次数为1 000次,训练目标为0.000 1,学习速率为0.1;遗传算法最大迭代次数为30,染色体种群数目为40,交叉概率取0.7,变异概率取0.01;蚁群算法最大迭代次数为100,蚂蚁数量为30只,信息素挥发系数为0.3,信息素常量Q取0.001,信息素初始浓度设为1。
用GACO-BP算法和基本ACO-BP算法分别对上述归一化后的样本数据进行训练。图2为基于2种算法的模型的训练误差(归一化样本的实际输出值与期望输出值之间的均方误差)下降折线图。从图2中可看出,GACO-BP算法迭代训练的起始误差比基本ACO-BP算法的小;基本ACO-BP算法迭代次数为80次左右时才达到最终收敛误差,而GACO-BP算法在20次左右就已经达到,且最终收敛误差明显小于基本ACO-BP算法。上述结果说明用遗传算法来改进蚁群神经网络算法使其在时间效率和求解效率方面均有了一定程度的提高,通过遗传算法和蚁群算法的优势互补,不仅加快了算法逼近最优解的收敛速度,而且提高了最优解的精度。

图2 训练误差下降曲线对比Fig.2 Comparison of training error curves
将上述最优解对应的权值组合作为BP神经网络的初始权值,进一步训练神经网络,得到的输出结果通过反归一化还原成大坝径向位移的拟合值。图3为GACO-BP模型和多元回归模型的拟合曲线,多元回归模型、GACO-BP模型的拟合均方根误差分别为0.602,0.078 mm。由图3可以看出,GACO-BP模型拟合效果很好,多元回归模型相对差一些。
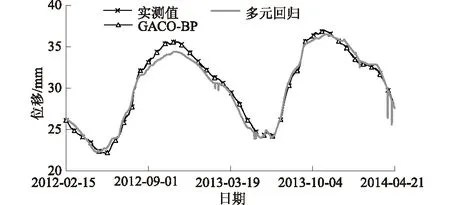
图3 模型拟合曲线Fig.3 Fitting curves of models
用上述GACO-BP模型训练好的神经网络进行预测,反归一化后可得到大坝径向位移的预测值。
3.2 MC模型修正残差
根据马尔科夫链原理,将实测值与GACO-BP模型拟合值之间相对误差取值区间划分为4个状态,结果见表1,由此确定相对误差序列全部样本的状态。

表1 状态划分Table 1 Classification of states
利用马尔科夫链分析相对误差序列,可得到m步(m=1,2,3,4)状态转移矩阵为:
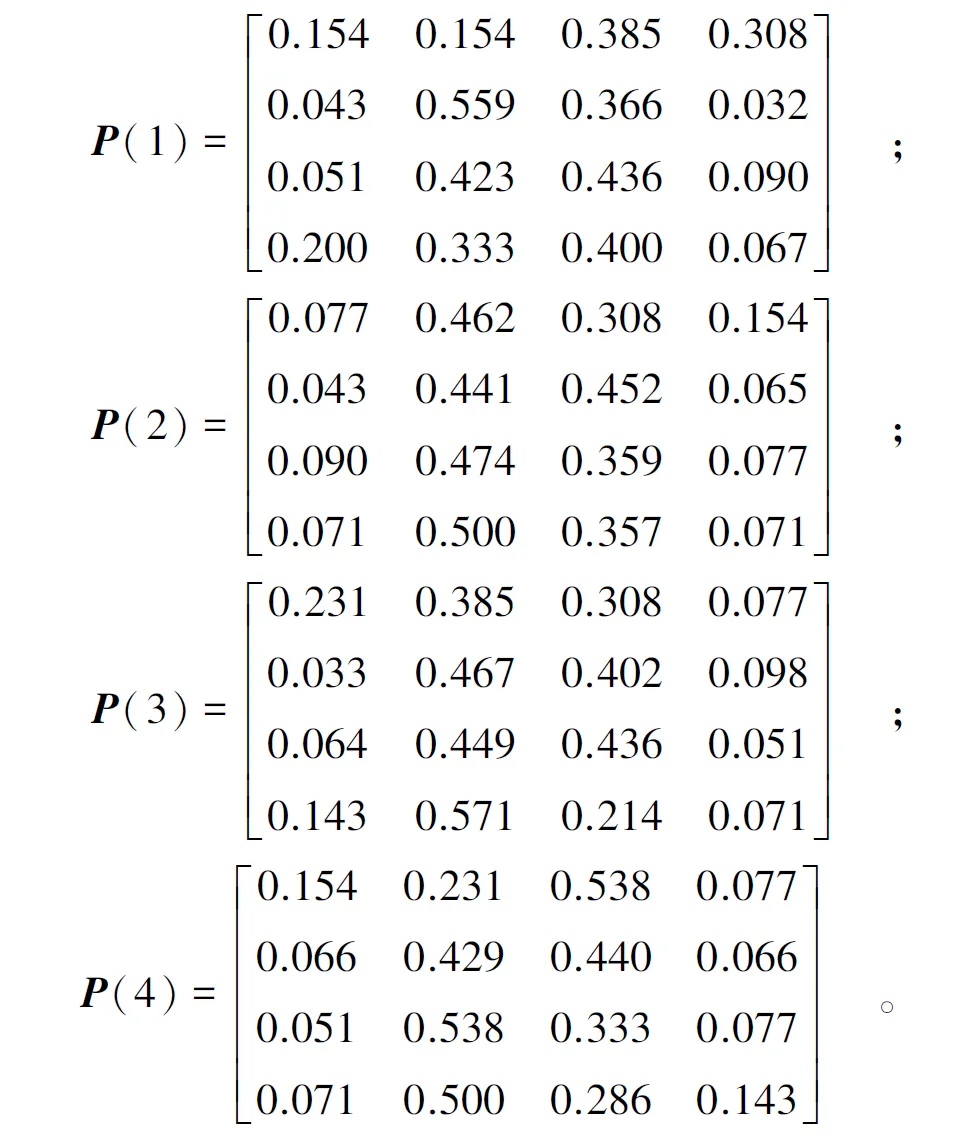
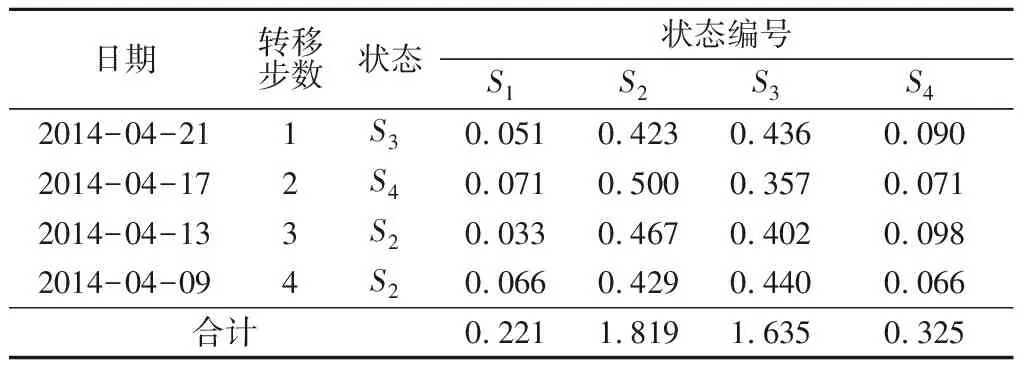
以2014年4月25日的径向位移为例,选取距其最近的4个数值(样本序列中第197~200个数据)来预测其预测值相对误差所处的状态,结果见表2。
表2 2014-04-25径向位移的相对误差状态预测
Table 2 Predicted relative error state of radialdisplacement on April 25, 2014
日期转移步数状态状态编号S1S2S3S42014-04-211S30.0510.4230.4360.0902014-04-172S40.0710.5000.3570.0712014-04-133S20.0330.4670.4020.0982014-04-094S20.0660.4290.4400.066合计0.2211.8191.6350.325
由表2可知,其预测值的相对误差处于S2状态的可能性最大,对应的状态区间为[-0.4,0),则根据式(16),可计算出由MC模型修正的2014年4月25日径向位移预测值为
2014年4月25日径向位移的实测值26.944 mm,GACO-BP模型预测值为26.979 mm,由此可见,GACO-BP-MC预测模型可以有效地提高预测精度。
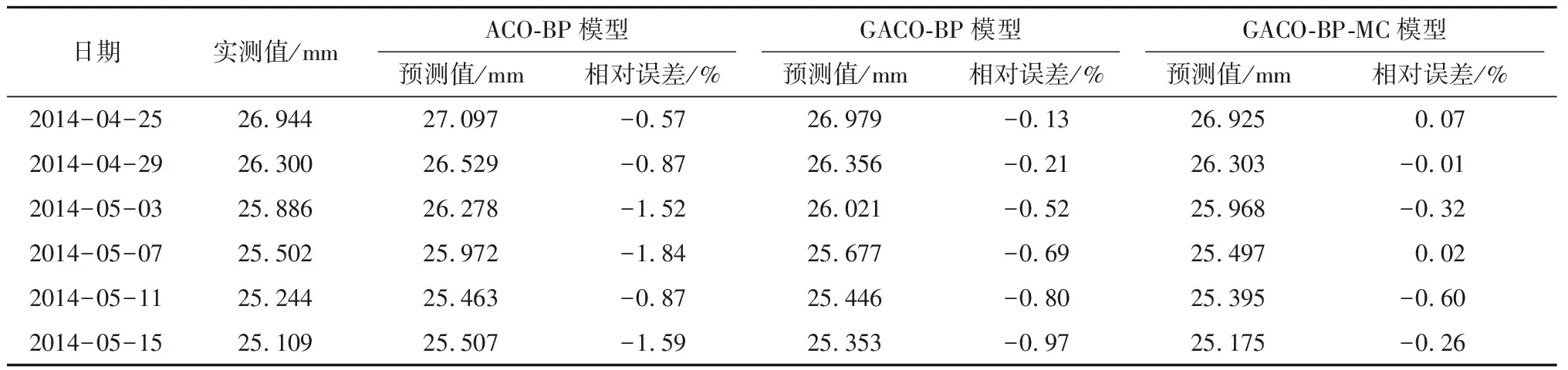
将2014年4月25日的预测值加入原样本序列,并剔掉第1个数据,构成新的样本序列,重复GACO-BP-MC模型的预测过程依次进行2014年4月29日至2014年5月15日径向位移的预测,不同模型预测结果见表3。
表3 不同模型的预测结果比较
Table 3 Comparison of predicted result among different models
日期实测值/mmACO-BP模型GACO-BP模型GACO-BP-MC模型预测值/mm相对误差/%预测值/mm相对误差/%预测值/mm相对误差/%2014-04-2526.94427.097-0.5726.979-0.1326.9250.072014-04-2926.30026.529-0.8726.356-0.2126.303-0.012014-05-0325.88626.278-1.5226.021-0.5225.968-0.322014-05-0725.50225.972-1.8425.677-0.6925.4970.022014-05-1125.24425.463-0.8725.446-0.8025.395-0.602014-05-1525.10925.507-1.5925.353-0.9725.175-0.26
图4为不同模型的预测值曲线和实测值曲线对比。由图4可知,GACO-BP-MC模型相比于其他2种模型,可以较大地提高预测值精度。
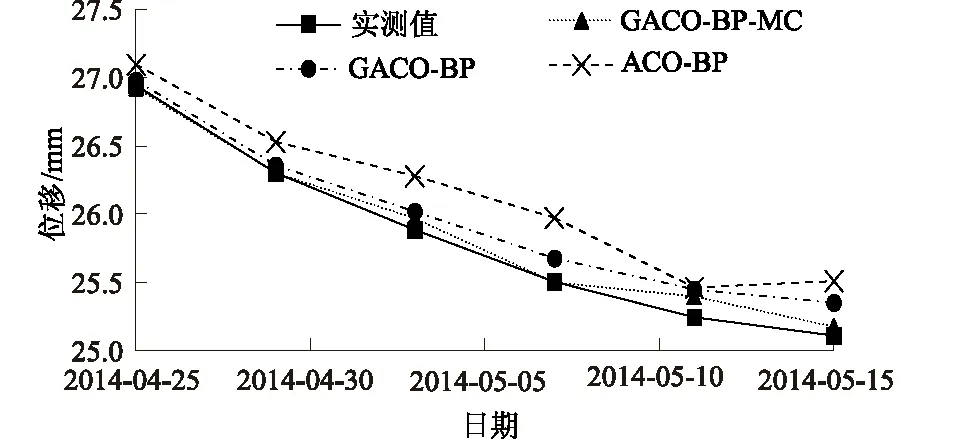
图4 不同模型预测值曲线Fig.4 Curves of predicted result of different models
4 结 论
本文建立了基于GACO-BP-MC的大坝变形监控模型,其原理是通过引入遗传算法改进基本ACO-BP模型来拟合和预测大坝变形发展规律,然后利用马尔科夫链修正残差,来进一步提高预测的精度和可靠性。通过工程实例分析,得到如下结论:
(1)GACO-BP-MC模型在寻参过程中结合了遗传算法和蚁群算法来对BP神经网络的权值进行训练优化, 既具有遗传算法的快速全局搜索能力, 又充分发挥了蚁群算法的正反馈优势, 大大减少了蚁群算法的搜索时间和迭代次数, 加快了逼近最优解的收敛速度, 具有更高的时间效率和求解效率, 且避免陷入局部极小值, 一定程度上弥补了ACO-BP模型的缺陷。 利用马尔科夫链对模型拟合残差进行辨识处理, 以此修正预测值,进一步地提高了预测精度。
(2)GACO-BP-MC模型预测值与实测值的相对误差相较于GACO-BP模型和ACO-BP模型有了明显减小,且与传统的多元回归模型和ACO-BP模型相比,GACO-BP-MC模型拟合值的均方根误差更小,非线性拟合能力明显提高,这说明GACO-BP-MC模型具有更高的拟合和预报能力,能更好地适用于大坝变形的监控,在大坝安全监测领域具有一定的推广应用价值,可考虑在此基础上建立更复杂的大坝安全预警模型。
