交通荷载作用下焦作地区饱和粉质黏土变形特性及影响因素分析

(中国地质科学院 水文地质环境地质研究所，石家庄 050061)

1 研究背景

随着我国经济快速发展，城市交通工程的建设速度也越来越快。许多重要交通基础设施建设在深厚地基土之上，这些工程竣工投入运营后，交通荷载所引起的岩土工程问题越来越为人们所关注。例如上海地铁建成投付使用以后，发现隧道中行驶列车的振动对隧道周围土体强度和变形有较大的影响(隧道轴线的沉降明显)，而且这种影响与地铁列车状态有很大的相关性[1]；温州永强机场在工程竣工3 a后的工后沉降量达到149 mm，竣工4 a后的工后沉降量达到166 mm，2013年沉降量已达555 mm，超过设计标准值近10倍[2]。这些沉降一部分是由路堤静荷载下未完成的主固结和次固结所造成的，还有很大一部分源自交通荷载的长期循环作用。焦作市在河南地层区划中处于华北地层区山西分区和华北平原分区结合部位，北部山区出露有古生界寒武系、奥陶系和石炭系，山前平原分布大面积第四系堆积物。太行山以南广大平原区地势平坦，广泛分布第四纪典型粉质黏土，地壳稳定性好，具有强震少、频度低、地震破坏性程度小三大特点，成为工程建设及交通荷载的重要基础层位。目前焦作市区经济建设正在蓬勃发展，高铁、地铁等重大交通建设也在未来规划之中，在这些交通建设进行之前，正确分析和研究长期交通荷载作用下该地区地基土动力变形特征对保证交通设施的安全运营具有重要意义。

表1 原状粉质黏土物理性质及力学指标Table 1 Physical properties and mechanical indexes of raw silty clay

目前国内外学者针对砂土、粉土、软黏土等进行了大量土动力特性方面的研究，且对于地震荷载主要集中在砂土、粉土地基液化方面[3-8]，而对于长期循环荷载则主要研究软黏土和重塑土的孔压和变形特征[9-15]，对于交通荷载作用下强度较高的粉质黏土动力特性研究不多。余周[16]利用动三轴仪器通过改变围压、固结比试验参数研究了饱和粉质黏土的变形特性，得出了围压、固结比与土体动强度、动弹性模量及动阻尼比的关系。霍海峰[17]分别研究了围压、固结比、动应力比以及振动频率对动荷载作用下饱和原状与重塑粉质黏土动力特性的影响，并进行了对比分析。谢琦峰等[18]对宁波饱和重塑粉质黏土进行了动三轴试验，提出采用相对动应力来分析不同围压、不同动应力下土的累积塑性应变变化规律。黄娟等[19]研究了昆明泥炭质土在循环荷载作用下的动变形特性，从动骨干曲线、应力-应变滞回曲线和动弹性模量等方面重点分析了围压、固结比、加载频率对泥炭质土变形特性的影响。

本文结合前人的研究成果，以焦作地区典型饱和粉质黏土为研究对象，采用振动三轴仪进行不同条件下单样多级加载和平行多样恒定幅值加载试验，从应变-振动次数变化曲线、动应力-应变滞回曲线2个方面分析了不同围压、固结比、动应力、振动频率下饱和黏性土的动应变特性，为研究高铁、地铁等大规模交通建设提供可靠的依据。

图1 原状土颗粒级配曲线Fig.1 Gradation curveof undisturbed soil

2 饱和粉质黏土动三轴试验

2.1 土样物理性质及力学指标

试验土样取自焦作市北部平原区，属于典型第四系上更新统冲洪积层粉质黏性土原状土，含有机质、钙核、少许小砾石，取样深度为4～6 m，地下水位埋深8 m。表1为原状土物理性质及力学指标，由表1可知塑性指数Ip≤17，试样为粉质黏土；液性指数IL介于0.22～0.24之间，试样处于硬塑状态。从原状土样的压缩曲线上确定出试样的先期固结压力Pc为110 kPa左右，经计算所取原状土样位置的上覆土体自重应力P1为90 kPa左右，由此可判定本次动三轴试验中的土样为超固结土，超固结比OCR约为1.2。图1为原状土颗粒级配曲线，可看出试样黏粒含量高，粒径较小，土粒分布较均匀，级配较差。

2.2 试验仪器与步骤

2.2.1 试验仪器

动三轴仪型号为美国GCTS公司生产的STX-300，可直接数字伺服控制轴向荷载、围压和孔隙水压，能够进行各向同性和各向异性固结、饱和土的常规静三轴测试 (UU、CU和CD)、高级静三轴测试(应力路径和应变路径)、动三轴测试(应力路径、动剪切强度和变形、残余模量、液化势分析、剪切模量、阻尼比和复杂模量等)。除此之外该系统还可以进行双向振动三轴(动态双向加载)试验。

2.2.2 试验步骤

在室内依据《土工试验规程》(SL 237—1999)利用削土器将现场取得的原状粉质黏土土样制成直径50 mm、高100 mm的原柱体试样；放入保护容器内抽气饱和，然后放入压力室内进行反压饱和(饱和度在98%以上)；施加设定的围压和轴压在静力下完成固结；设置好试验参数(振动次数、频率、振动波形等)后施加动荷载。

2.3 试验工况

本次试验模拟交通荷载对原状饱和粉质黏土的作用过程，主要考虑了围压、固结应力比、振动幅值、振动频率的影响。其中，根据现场的勘察资料及原状样的取土深度确定围压范围约为50 kPa，试验中分别选取了50，100 kPa两种不同的围压；固结应力比(Kc=σ1c/σ3c)可模拟土体不同的初始受力状态，根据土样的静力强度并结合围压的大小，试验中采用等压固结Kc=1.0与偏压固结Kc=1.2，1.4；振动频率反映了车辆行驶速度的变化，根据现场实测资料，列车行驶过程中振动频率是不断变化的，车速越高振动频率越快，而目前高铁的运行时速已经超过300 km/h，且今后仍有不断增加的趋势，借鉴前人的研究成果并结合测试仪器的范围，主要采用频率f=5.0 Hz进行试验，并与f=1.0 Hz和2.5 Hz进行对比分析。

交通荷载有别于地震荷载和波浪荷载[20]，行驶车辆在地基中引起的动应力在竖直方向上幅度最大，成为室内试验中的主要模拟对象。目前对于交通荷载振动形式的模拟主要分为正弦波与半正弦波2种。实际上，现有的数值模拟与实测资料表明，行驶车辆在地基中引起的动应力与车重、车速、车辆-路堤-地基系统相对刚度等因素有关[21]，与拉压等幅的半正弦波差距很大，和仅有压半周的半正弦波较为接近，因此本次试验中动应力加载模式采用半正弦波形。

本次试验分为单样多级加载和平行多样恒定幅值加载，每次加载均振动5 000次，当轴向累积应变达到5%时定为破坏标准，超过12%或加载次数达到设定值时，试验终止。由于交通荷载作用下饱和土体几乎不发生排水和体积变化，试验采用不排水三轴模拟。单样多级及平行多样恒定幅值加载具体试验方案分别如表2、表3所示。

表2 单样多级加载试验方案及成果Table 2 Schemes and results of multistage loading test onsingle specimen

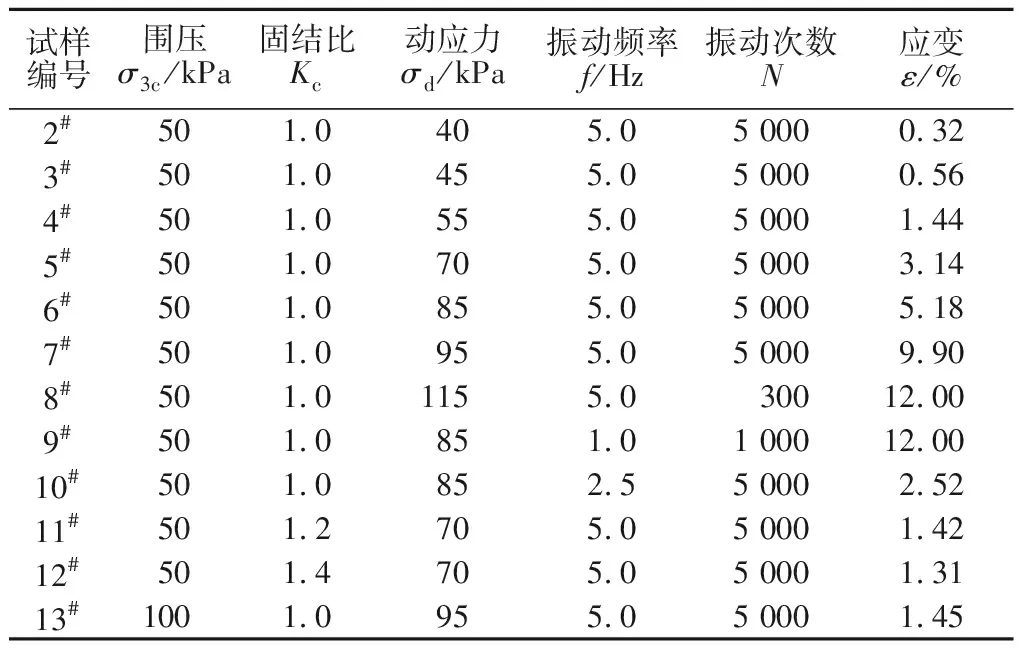
表3 平行多样恒定幅值加载试验方案及成果Table 3 Schemes and results of loading test on parallelspecimens with constant amplitude

2.4 试验数据处理

根据仪器计算系统记录的试验数据，绘制出不同试验条件下的应变-振动次数曲线及动应力-应变滞回曲线。对于滞回曲线，以不同振动次数下初始应变值为标准进行归一化处理，便于对每个循环内的应变变化进行比较。

3 饱和粉质黏土动变形特性及影响因素分析

3.1 不同动应力下试样变形特性

在单样多级加载过程中， 试样1#进行等压固结， 振动频率为5 Hz， 进行6级加载， 每级振动次数均为5 000次， 最后一级加载时试样产生破坏， 试验停止。 图2为单样多级加载应变随振动次数变化曲线， 可以看出在1～6级加载过程中， 应变分别为： 0.32%， 0.47%， 0.95%， 1.60%， 2.69%， 8.03%， 其发展模式主要为稳定型和破坏型2种， 很少出现前人研究得出的临界型。 在动应力达到125 kPa时， 初始振动阶段应变增长较快， 一定振动次数后增长速率减缓， 应变随振动次数的增加几乎不再发生变化， 逐渐趋于稳定， 应变发展模式都为稳定型； 当动应力达到125 kPa后， 应变随振动次数增长速率加快， 试样在较低振动次数内产生破坏， 发展模式属于破坏型， 而在σd=110 kPa时， 试样应变为2.69%， 未达到破坏标准， 这说明单样多级加载过程中试样可能存在产生破坏的临界动应力值， 这个值介于110～125 kPa之间。

图2 单样多级加载应变随振动次数变化曲线Fig.2 Variation of strain with vibration times forsingle specimen under multistage loading

图3 平行多样恒定幅值加载应变随振动次数变化曲线Fig.3 Variation of strain with vibration times forparallel specimens under constant amplitude

在平行多样恒定幅值加载过程中，分别对试样2#，3#，4#，5#，6#，7#，8#在不同动应力下振动5 000次，加载结束后试样产生不同的应变。图3为平行多样恒定幅值加载应变随振动次数变化曲线，可以看出不同动应力下产生的应变分别为0.32%，0.56%，1.44%，3.14%，5.18%，9.90%，12.00%，随着动应力的增大每个试样的应变不断增大。应变发展模式和单样多级加载时相同，都为稳定型和破坏型，不同的是应变随动应力的变化存在明显临界动应力且小于单样逐级加载中的临界值，这个值在95 kPa左右，此时试样应变达到9.9%，已经产生了破坏。图4为平行多样恒定幅值加载不同动应力对应的最终应变关系，可以看出当动应力小于临界动应力时，应变都未能达到破坏标准，当动应力超过临界动应力时，应变随动应力变化存在一个明显拐点，在这个拐点后应变急剧上升。这说明动应力对应变的影响较大，动应力超过临界动应力时试样内部结构才会产生破坏，强度急剧降低。此外，单样多级加载试样产生破坏所需的动应力较恒定幅值加载时大，其原因是单样多级加载试验中前几级动应力加载对试样产生了振动压密的作用使土样密实度增加、强度增大，从而不易产生破坏。

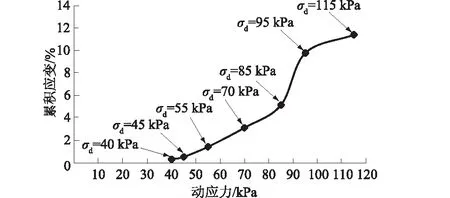
图4 多样恒定幅值加载不同动应力对应的最终应变曲线Fig.4 Ultimate strain curve corresponding to differentdynamic stresses for parallel specimens under constantamplitude

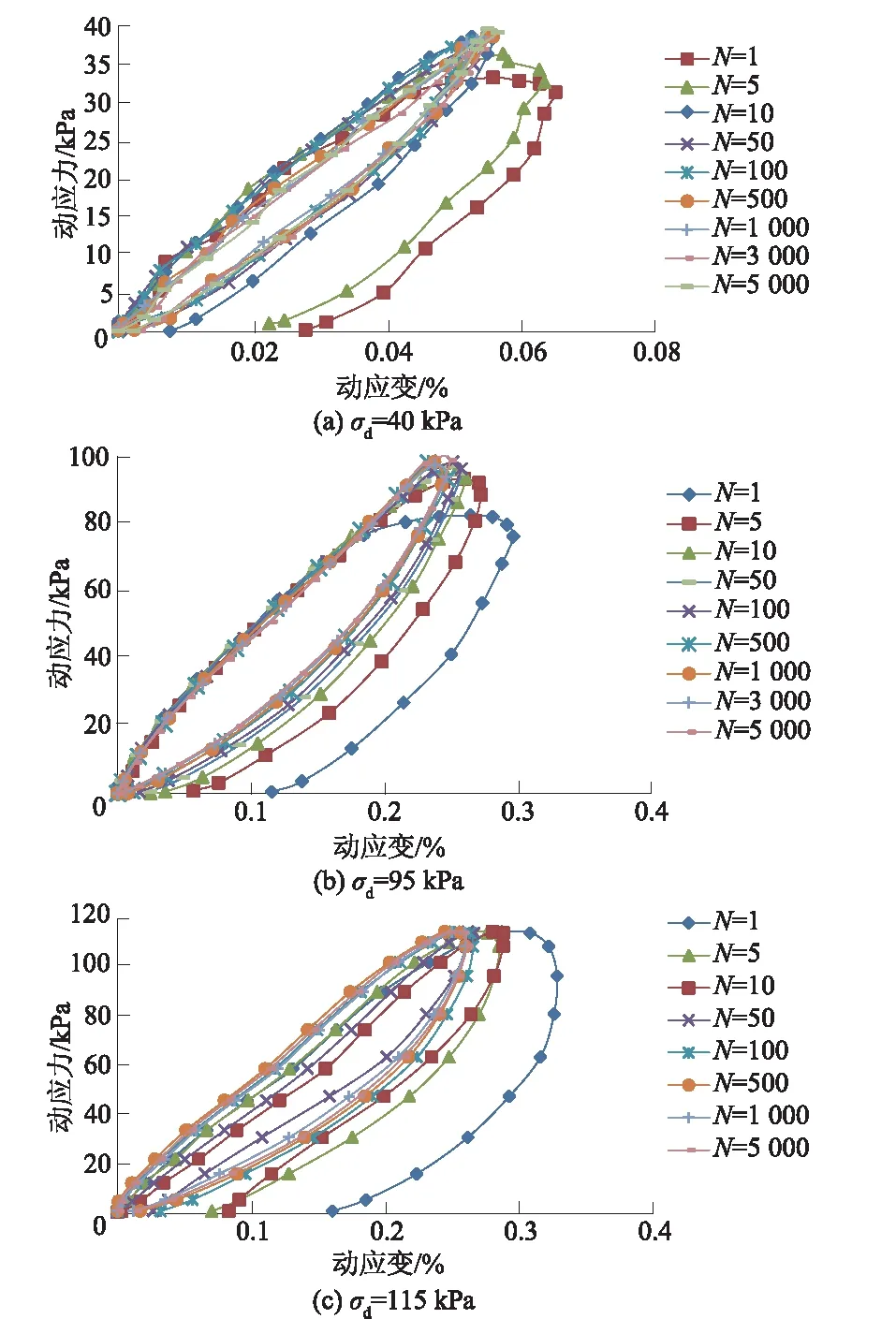
图5 不同动应力不同振动次数下应力-应变滞回曲线Fig.5 Stress-strain hysteretic curves under differentvibration times and dynamic stress levels

不同动应力下应力-应变滞回曲线如图5所示。从图5(a)可以看出在动应力σd=40 kPa下N=1时最大动应变为0.069%，随着振动次数的增加，每个周期内的应变最大值逐渐减小，N=5时最大应变为0.063%，N=50时最大应变为0.055%，变化差异比较明显，在N=100后应变变化趋于稳定，N=5 000后也没有发生太大的变化，最终应变保持在0.053%左右。在整个加载过程中，随着振动次数的增加，每个周期内应变最大值逐渐减小最后趋于稳定，滞回曲线随之先向纵轴倾斜后趋于稳定。这是因为在振动加载过程中土样的刚度发生了变化，在振动初期应变较小，处于弹性变形阶段，回弹量较大，随着振动次数的增加土样密实度增加，强度增大，出现了应变硬化现象。

从图5(b)中可知在动应力σd=95 kPa时，随着振动次数的增加，每个周期内应变最大值不断减小，相比于动应力σd=40 kPa时变化幅度较小，在N=500以后基本保持稳定，滞回曲线斜率几乎不再发生变化。从图5(c)可以看出在动应力σd=115 kPa时，滞回曲线的变化规律与动应力σd=40 kPa和95 kPa不同，每个周期内应变最大值先逐渐减小并趋于稳定，一定振动次数后又开始逐渐增大，在N=5 000时的应变量与N=100时较为接近。这说明由于动应力超过了临界动应力值，应变变化迅速，在振动初期由于振动压密作用土样很快产生硬化，但这个过程很短暂。在应变达到破坏标准之后，内部结构产生破坏，强度急剧降低，出现软化现象。

结合上述分析，为比较相同振动次数不同动应力下饱和粉质黏土滞回曲线变化情况，对N=10时滞回曲线进行了分析。如图6所示，可以看出动应力σd=40 kPa时振动周期内的应变最大值为0.062%，相比于动应力σd=95 kPa作用下产生的0.255%要小很多，这说明动应力对试样变形影响显著，动应力越大变形越大，差距越明显。此外，不同动应力下滞回圈的形态也发生了变化，随着动应力的增加滞回圈的面积增大，圈内对应两点的距离拉长，两端点连线的斜率减小，滞回圈中心向右偏移。这说明相同条件下动应力越大对土体结构破坏性越强，土体塑性累积应变越大，产生的可恢复性弹性变形相应越小。

图6 相同振动次数(N=10)不同动应力下应力-应变滞回曲线Fig.6 Hysteretic curves of strain under differentdynamic stress levels vibrated for 10 times

3.2 不同围压下试样变形特性

围压反映了试样深度的变化，围压越大代表模拟土样所处的位置越深。本次研究分别对试样7#、13#进行了相同条件不同围压下试样动变形对比试验。图7为不同围压下试样应变与振动次数变化关系，可以看出σ3c=100 kPa下轴向累积应变发展缓慢，振动5 000次后稳定在1.83%左右，土样并未产生破坏，应变发展模式属于稳定型；σ3c=50 kPa下轴向累积应变发展迅速，振动2 500次时试样应变便超过5%，最终应变达到11%，土样产生破坏，应变模式属于破坏型。这说明相同条件下围压越大试样变形越小，围压增大会使土体强度升高，结构更不易破坏，试样产生破坏所需的动应力更大。

图7 不同围压下应变随振动次数变化关系(σd=95 kPa)Fig.7 Relationship between strain and vibrationtimes under different confining pressuresat given dynamic stress(σd=95 kPa)

相同振动次数(取N=10)不同围压下应力-应变滞回曲线如图8所示，可以看出围压σ3c=100 kPa与围压σ3c=50 kPa下振动周期内产生的应变最大值分别为0.25%和0.28%，围压越大相同动应力作用下产生的应变越小，滞回圈内对应两点的距离拉长，两端点的连线的斜率增大。这说明相同动应力下，围压增大后土体的强度增加，内部结构不易破坏，土体弹性能增强，土体产生的可恢复弹性变形相应越小，轴向变形累积缓慢。

图8 不同围压下动应力-应变滞回曲线(N=10)Fig.8 Dynamic stress-strain hysteresis curves ofspecimen under different confining pressuresvibrated for 10 times

3.3 不同振动频率下试样变形特性

动三轴试验中所设定的振动频率不同反映了车辆行驶速度的变化，车速越快相应振动的频率越高。本次研究分别对试样6#，9#，10#进行了不同频率下的动力加载试验。图9为围压50 kPa不同振动频率下轴向应变与振动次数变化关系，可以看出，频率f=1 Hz时振动1 000次后轴向变形达到12%；频率f=5 Hz时振动5 000次后轴向变形为5.18%；而频率f=2.5 Hz时振动5 000次后轴向变形仅为2.52%。

图9 围压σ3c=50 kPa不同振动频率下轴向应变随振动次数变化关系Fig.9 Relationship between axial strain and vibrationtimes at different vibration frequencies under50 kPa confining pressure

图10 不同频率对应的累积应变关系Fig.10 Ultimate strain relationship corresponding todifferent frequencies

图10为不同频率下对应的累积应变关系，可知振动频率f=1 Hz下动应力对土样变形产生的影响最大，随着频率的增大相同振动次数下动应力对土样产生的变形减小，但并不是频率越大土样产生的变形就越小，因为从图10中明显看到频率f=5 Hz产生的应变量要大于频率f=2.5 Hz，频率f=1 Hz和5 Hz均使土样产生了破坏，只是所用的振动次数不同，而频率f=2.5 Hz在振动5 000次后土样仍具有较高的强度。这说明频率对土体变形的影响可能存在一个临界值fc，在未达到临界频率值前动变形逐渐增大，在超过fc后动变形增幅开始减小，频率越接近这个临界值土体产生的变形越小。频率f=2.5 Hz可能超过了临界振动频率值，也可能未达到，但相比于f=1 Hz和5 Hz更为接近。振动频率模拟的是列车行驶速度，速度越快频率越高，对应列车运行速度对地基土变形的影响也应可能存在一个临界速度值，越接近临界速度地基土产生的变形越小。这可能与土体自身振动频率、物理性质及仪器性能有关，以后会设计试验进一步研究。

相同振动次数(取N=10)不同振动频率应力-应变滞回曲线如图11所示，可以看出不同振动频率下滞回圈形态不同，f=1 Hz时循环周期内最大应变为0.36%，频率增大到2.5 Hz时最大应变值减小为0.20%，滞回圈对应两点的距离缩小，两端点的连线向纵轴靠近，滞回圈中心向左移动；当f=5 Hz时最大应变值达到0.23%，仍小于f=1 Hz时的最大应变值，但大于f=2.5 Hz时的最大应变值，相比于f=2.5 Hz时的滞回圈对应两点距离拉长，两端点连线的斜率减小，滞回圈斜率向右平移。可以解释为由于振动频率不同，在同一循环周次内相应动应力对土样的作用时间也就不同，动应力加载时对土体结构产生冲击，卸载时土体结构部分恢复，但这个过程需要一定的时间，当频率较高时，动应力作用过程较快，产生的应变量较小，每次作用时间间隔短暂，卸载过程结构可能只有部分恢复或是根本没有时间来得及恢复。当频率较低时，动应力作用过程较慢，时间间隔较长，动应力次加载产生的应变量较大，卸载过程土体结构有一定时间进行大部分恢复。频率不同会导致土体的加卸载过程产生的应变量和恢复量有所差异，对土体的刚度产生影响，但不是频率越大土体刚度降低越快，而是存在一个临界振动频率值，当所施加的频率接近临界值时土体刚度降低缓慢，内部结构不易破坏，轴向变形不易累积。

图11 不同振动频率下应力-应变滞回曲线Fig.11 Hysteresis curves of different vibration frequencies

3.4 不同固结方式下试样变形特性

不同的固结方式反映了土体不同的初始受力状态，偏压固结可模拟土样在承受动荷载前除上覆土体自重荷载以外未来可能存在的静荷载产生的影响。本次研究分别对试样5#、11#、12#进行了不同固结比的动力加载试验。图12为不同固结比下试样应变与振动次数变化关系，可以看出各固结比条件下轴向应变随振动次数先增长后趋于稳定，固结比Kc=1.0，1.2，1.4条件下产生的轴向应变量不大，分别为1.65%，1.36%，1.22%，应变发展模式均属于稳定型。相同动应力σd=70 kPa条件下，固结比越大试样最终轴向累积应变越小，这是因为围压一定的条件下，固结比越大，轴向固结压力就越大，土样轴向压密程度越高，使其强度增大，抵抗弹性变形的能力增强，轴向塑性累积变形发展缓慢。

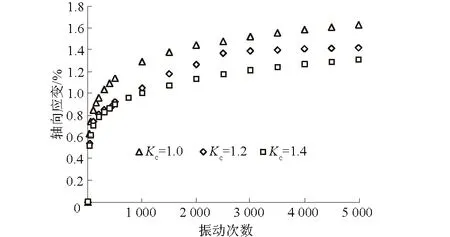
图12 σd=70 kPa不同固结比应变随振动次数变化关系Fig.12 Relationship between strain and vibrationtimes at different consolidation ratios(σd=70 kPa)

相同振动次数(取N=10)不同固结比滞回曲线如图13所示，可以看出不同固结比下试样在动应力作用下产生的动应变不同，固结比Kc=1.0，1.2，1.4条件下周期内最大应变分别为0.17%，0.12%，0.07%。试验表明固结比越大动应变越小，滞回圈对应两点的距离缩小，两端点连线的斜率增大，滞回圈中心向纵轴平移。这是由于固结比增大后，在施加动应力前轴向的压密作用使土体的强度增大，内部结构不易破坏，土体可恢复的弹性变形减小。

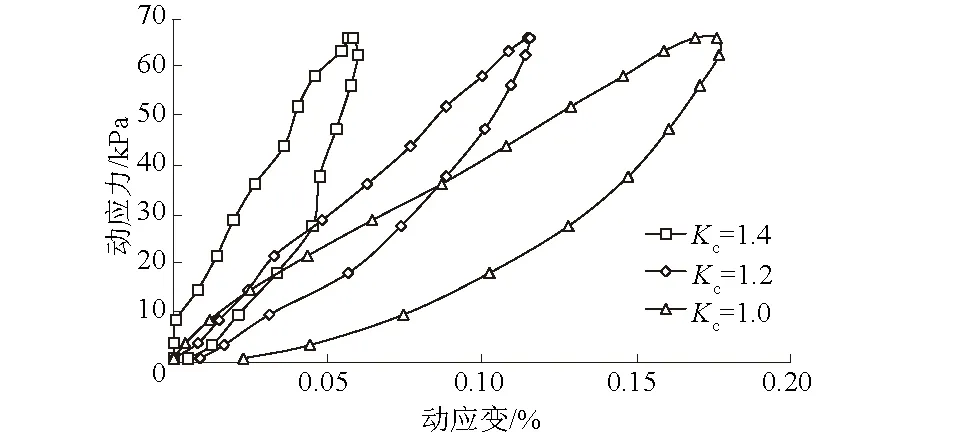
图13 σd=70 kPa不同固结比动应力-应变滞回曲线Fig.13 Dynamic stress-strain hysteresis curves atdifferent consolidation ratios (σd=70 kPa)

4 结 论

(1)不同加载方式对土体变形特性会产生不同的影响。单样多级加载过程使土体密度增加，强度升高，结构不易产生破坏；平行多样恒定幅值加载时，不同动应力对土体变形的影响存在一个明显临界动应力，超过这个值后试样变形量急剧增加，较低振动次数内便产生破坏。

(2)动应力对土体变形特性影响较大。动应力小于临界动应力时，随着振动次数的增加滞回圈面积先减小后趋于稳定，两端点连线的斜率先增大后保持稳定，出现硬化现象；动应力超过临界动应力后，滞回圈面积随振动次数变化先减小后稳定，后期又开始逐渐增大但不会超过N=1时的面积。后期滞回圈面积又逐渐增大说明此时试样结构开始产生破坏，出现软化现象。

(3)围压与固结比对土体强度影响显著。相同条件下，围压与固结比增大后土体产生的变形减小，土体的强度增加，产生可恢复的弹性变形减小，轴向变形不易累积。

(4)振动频率对土体动变形会产生一定的影响。振动频率模拟的是列车行驶速度，速度越快频率越高，但不是频率越高试样产生的塑性变形越小，而是可能存在一个临界振动频率值，在这个值前后土体的变形都会增大。这说明列车运行对地基土变形的影响也应可能存在一个临界速度，越接近临界速度地基土产生的变形越小。