磁悬浮双转子系统的模态与不平衡响应分析
2019-07-28叶春王念先王东雄
叶春,王念先,王东雄
(武汉科技大学 a.冶金装备及其控制教育部重点实验室;b.机械传动与制造工程湖北省重点实验室,武汉 430081)
传统的航空发动机双转子系统一般采用滚动轴承支承,会引入复杂的轴承腔、腔密封装置、密封增压系统、润滑系统和冷却系统等。磁悬浮轴承是新型的机电一体化设备,具有无机械摩擦,无润滑,高转速,高可靠性,长寿命及支承特性主动可控等优点。用磁悬浮轴承代替传统滚动轴承,利用其支承刚度主动可调的特点,有望通过改变磁轴承支承刚度,达到对双转子系统固有特性和振动响应特性的主动调控。
固有特性和不平衡响应特性是双转子动力学研究的重点。文献[1-4]对双转子系统进行模态分析,研究了离心力、运行状态、支承刚度等对双转子系统模态的影响;文献[5-6]用传递矩阵法计算了双转子系统的临界转速、振型及不平衡响应,研究了挤压油膜阻尼对系统动力学特性的影响。文献[7-10]对双转子系统进行不平衡响应分析,研究了转速比、旋转方向、不平衡质量及支承刚度等对双转子系统不平衡响应的影响。在磁悬浮转子方面,文献[11-13]计算了磁悬浮单转子的固有特性,研究了系统的刚性及柔性、支承刚度、附加阻尼等对系统固有频率、临界转速及振型的影响;文献[14-15]以磁悬浮单转子为研究对象,分析了阻尼器阻尼对系统模态及不平衡响应的影响;文献[16-18]分析了磁悬浮单转子系统的不平衡响应特性,探讨了不同的控制算法及控制策略对系统不平衡响应的影响。上述研究都是基于滚动轴承支承的双转子系统和磁轴承支承的单转子系统,对磁轴承支承的双转子系统的研究涉及较少;并且由于滚动轴承支承刚度难以在线调控,因而有关双转子系统振动的变刚度控制以及不同刚度下系统各模态对应的不平衡响应特性的研究很少。 鉴于此,现以磁悬浮双转子系统为研究对象,利用磁轴承支承刚度主动可调的特性,分析支承刚度对该双转子模态及不平衡振动的影响,研究其振动变刚度控制的可行性。
1 双转子系统模态分析
1.1 双转子系统结构
磁悬浮双转子系统结构如图1所示,其中内转子(用于模拟低压)与外转子(用于模拟高压)之间采用2套永磁轴承耦合连接实现悬浮支承,外转子采用2套电磁轴承实现悬浮支承。内转子右端与外转子左端分别通过弹性膜片联轴器与2个电动机主轴连接。
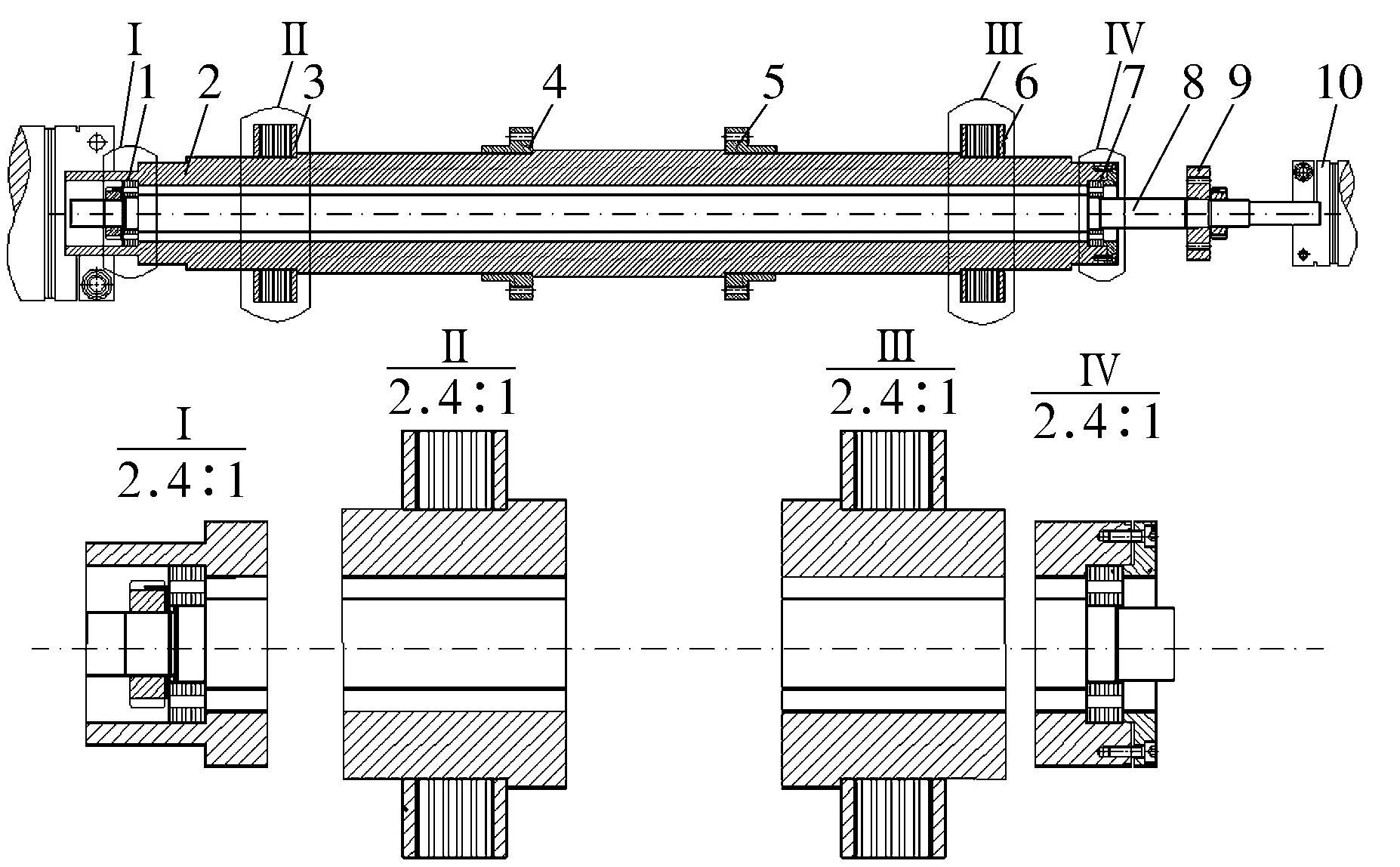
1,7—永磁轴承;2—外转子;3,6—电磁轴承转子;4,5—外转子导磁盘;8—内转子;9—内转子导磁盘;10—联轴器
1.2 双转子系统有限元模型
双转子系统的可控性由其内在因素模态决定,并且可以通过其不平衡响应直接反映。在有限元软件ANSYS中建立双转子系统模型(图2),对其进行模态及不平衡响应分析,双转子的主体部分采用SOLID187单元进行建模,将电磁轴承和永磁轴承简化为弹性支承,采用COMBIN14弹簧单元模拟,对系统进行一体化建模,材料密度为7 850 kg/m3,弹性模量为209 GPa,泊松比为0.269。
图2 双转子系统模型
在ANSYS中对内转子进行独立模态分析。假定外转子完全固定,则永磁轴承外圈固定,内圈与内转子相连,其支承刚度与双转子系统整体模态分析时的永磁轴承刚度相同。内转子有限元模型中永磁轴承等效为弹簧单元,一端与内转子外表面相连,另一端完全位移约束,其有限元模型如图3所示。

图3 内转子模型
在ANSYS中对外转子进行独立模态分析。假定内转子完全固定,则永磁轴承内圈固定,外圈与外转子相连,其支承刚度与双转子系统整体模态分析时的永磁轴承刚度相同;电磁轴承外圈固定,内圈与外转子相连,其支承刚度与双转子系统整体模态分析时的电磁轴承刚度相同。外转子有限元模型中永磁轴承等效为弹簧单元,其一端与外转子内表面相连,另一端完全固定约束;电磁轴承亦等效为弹簧单元,一端与外转子外表面相连,另一端完全固定约束,其有限元模型如图4所示。
图4 外转子模型
1.3 双转子系统模态振型分析
一般永磁轴承支承刚度k1为1×104~1×106N/m[19],电磁轴承支承刚度k2为1×105~1×107N/m[20]。实际电磁轴承存在一定阻尼,而永磁轴承的阻尼相对很小,故只在电磁轴承上施加一个较小的阻尼250 N·s/m。
在固有频率700 Hz以下,分别对内、外转子及双转子系统有限元模型进行模态分析。以k1=1×105N/m,k2=1×106N/m为例,内、外转子及双转子系统的模态振型见表1。

表1 内、外转子及双转子系统振型
由表1可知,在设定频率范围内,内转子有4阶模态:1阶固有频率为52.3 Hz,振型为绕内转子左侧锥动;2阶固有频率为76.4 Hz,振型为绕内转子中间靠右某点锥动;3阶固有频率为229.9 Hz,振型为典型一弯变形;4阶固有频率为589.1 Hz,振型为典型二弯变形。外转子有2阶模态:1阶固有频率为66.7 Hz,振型为绕外转子右端锥动;2阶固有频率为96.8 Hz,振型为绕外转子中间某点锥动。双转子系统有6阶模态:1阶固有频率为47.6 Hz,振型中内、外转子均为平动,且内转子变形远大于外转子;2阶固有频率为62.2 Hz,振型中外转子绕其左侧锥动,内转子其绕右侧锥动;3阶固有频率为71.8 Hz,振型中外转子绕其右侧锥动,内转子其绕左侧锥动;4阶固有频率为97.4 Hz,振型中外转子绕其中间锥动,内转子绕左侧锥动并伴有微小一弯变形;5阶固有频率为230.1 Hz,振型以内转子一弯变形为主,外转子几乎无变形;6阶固有频率为589.1 Hz,振型以内转子二弯变形为主,外转子几乎无变形。
对比可知,双转子系统前3阶模态的固有频率与内、外转子模态固有频率均不同,且系统中的转子振型与内、外转子独立模态振型也不同,故认为双转子前3阶模态为内、外转子混合激发;双转子系统第4阶模态的固有频率与外转子第2阶独立模态固有频率基本相同,且系统第4阶模态中外转子振型与外转子第2阶独立模态振型基本相同,故认为双转子第4阶模态为外转子激发;双转子系统第5,6阶模态固有频率分别与内转子第3,4阶独立模态固有频率基本相同,且双转子系统第5,6阶模态中内转子振型分别与内转子第3,4阶独立模态振型基本相同,故认为双转子第5,6阶模态为内转子激发。
由此可见,根据激发状态不同,双转子系统模态可以分为内转子激发、外转子激发及内、外转子混合激发这3类模态。
1.4 双转子系统固有频率分析
双转子系统不平衡振动变刚度的可控性在模态中可以体现在固有频率方面。系统固有频率反映了不平衡响应的峰值频率,只要系统固有频率随电磁轴承支承刚度发生变化,即可认为其不平衡振动是可控的。而对于固有频率不随电磁轴承支承刚度变化的情况,则需进行不平衡响应分析,判断其不平衡振动的峰值大小是否随电磁轴承支承刚度发生变化。若其峰值大小发生变化,则可控;否则不可控。
当k1在1×104~1×106N/m之间取定值时,分析双转子系统前6阶固有频率随k2的变化规律。以k1分别取1×104,1×105,1×106N/m为例,双转子系统前6阶固有频率随电磁轴承支承刚度的变化曲线如图5所示。
由图5a知,k1=1×104N/m时,双转子系统的5,6阶固有频率及k2为4×105~1×107N/m的系统1,2阶固有频率不随电磁轴承支承刚度变化,同时对比内、外单转子及双转子系统模态(表1)可知,此时双转子系统模态均为内转子激发;而双转子系统的3,4阶固有频率及k2为1×105~4×105N/m的系统1,2阶固有频率随电磁轴承支承刚度增大而增大,其模态均为外转子激发或内、外转子混合激发。

图5 双转子系统前6阶固有频率随电磁轴承支承刚度的变化曲线
同理,图5b中,k1=1×105N/m时,双转子系统的5,6阶固有频率及k2为4×106~1×107N/m的系统1,2阶固有频率几乎不随电磁轴承支承刚度变化,其模态均为内转子激发;而系统的3,4阶固有频率及k2为1×105~4×106N/m的系统1,2阶固有频率随电磁轴承支承刚度增大而增大,均为外转子激发或内、外转子混合激发。
图5c中,转子系统的5,6阶固有频率,k2为8×106~1×107N/m的系统1,2二阶固有频率及k2为1×105~2×106N/m的系统3,4阶固有频率几乎不随电磁轴承支承刚度变化,其模态均为内转子激发;而k2为1×105~8×106N/m的系统1,2阶固有频率及k2为2×106~1×107N/m的系统3,4阶固有频率随电磁轴承支承刚度增大而增大,均为外转子激发或内、外转子混合激发。
对比不同转子激发模态对应的电磁轴承刚度区间可知:当永磁轴承刚度较小(1×104N/m)时,系统1,2阶模态在低电磁轴承支承刚度区间(1~4)×105N/m为外转子激发或内、外转子混合激发,在高电磁轴承支承刚度区间4×105~1×107N/m为内转子激发;并且随着永磁轴承支承刚度的增大,外转子激发或内、外转子混合激发的模态会向高电磁轴承支承刚度区间扩展,内转子激发的模态会向高电磁轴承支承刚度区间收缩。当永磁轴承支承刚度较小时,系统3,4阶模态为外转子激发或内、外转子混合激发;当永磁轴承支承刚度增大到6×105N/m附近时,系统在低电磁轴承支承刚度区间开始出现内转子激发的柔性模态,并且随着永磁轴承支承刚度进一步增大,该模态会向高电磁轴承支承刚度区间扩展,此时外转子激发或内、外转子混合激发的模态会向高电磁轴承支承刚度区间收缩。在永磁轴承支承刚度一定时,系统5,6阶模态基本不随电磁轴承支承刚度变化,为内转子激发的柔性模态。
由此可见,双转子系统中外转子激发或内、外转子混合激发的模态固有频率随电磁轴承支承刚度增大而增大,其不平衡振动是可控的;内转子激发的模态固有频率不受电磁轴承支承刚度影响,其不平衡振动的可控性需通过不平衡响应分析中的振动幅值来判断。双转子系统各阶模态中,不同转子激发的模态对应的电磁轴承支承刚度区间随永磁轴承刚度变化而变化。
2 双转子系统不平衡响应分析
双转子系统的不平衡响应可以直观反映系统变刚度控制的可控性。实际双转子系统内、外转子上均存在不平衡量,故对双转子系统进行不平衡响应分析时,为接近实际情况,应在内、外转子上同时施加不平衡量。
当永磁轴承支承刚度一定,且变化区间为1×104~1×106N/m时,使内、外转子同向旋转,且转速比为1∶1.2,同时在内、外转子盘上施加1×10-5kg·m的不平衡量,分析电磁轴承支承刚度对其不平衡振动的影响。以k1=1×105N/m为例,其不平衡响应随电磁轴承支承刚度的变化如图6所示,其中内转子盘各曲线峰值情况见表2。
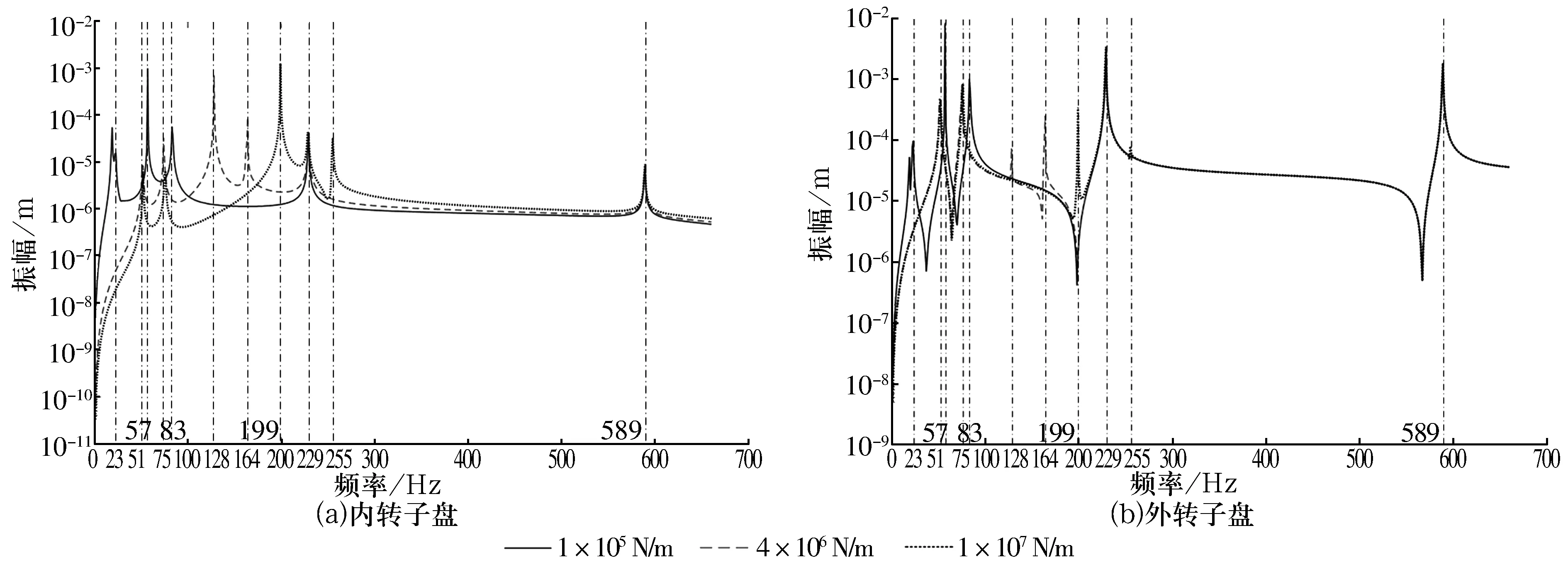
图6 k1=1×105 N/m时转子盘的不平衡响应随k2的变化
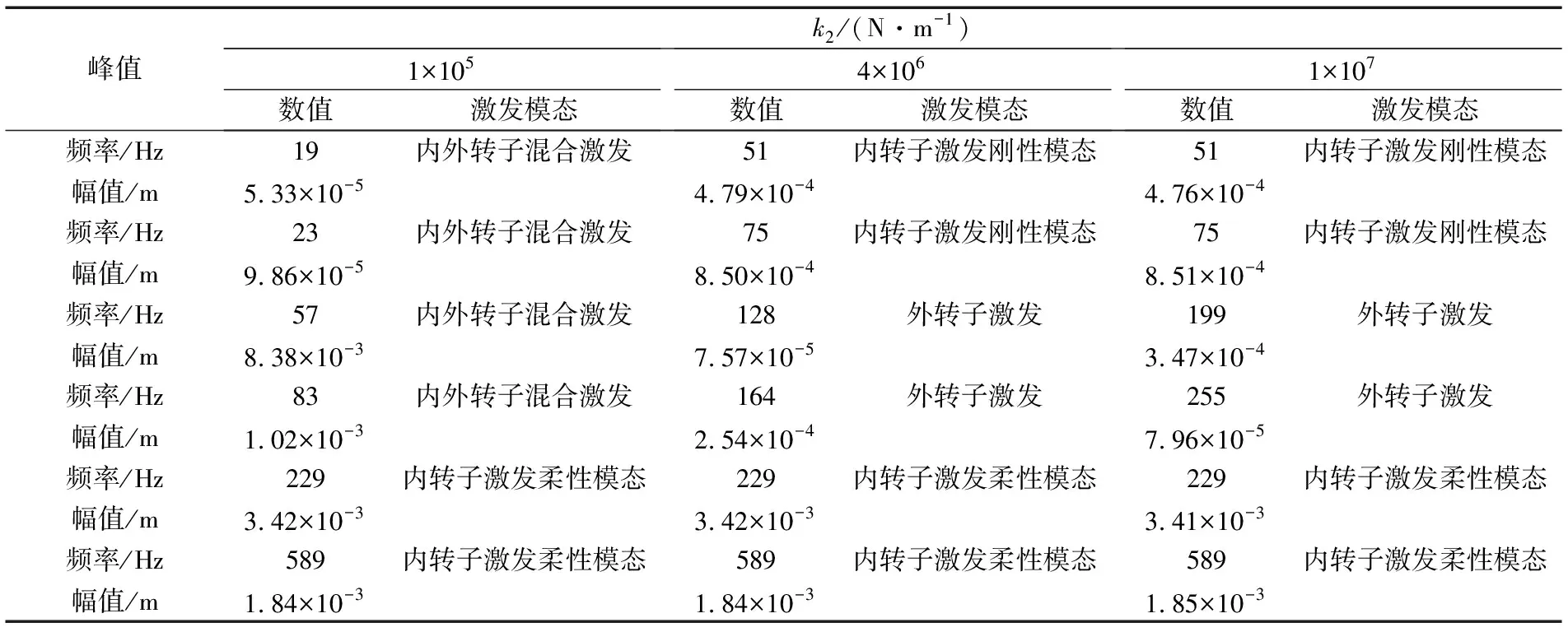
表2 不同电磁轴承支承刚度下的内转子盘不平衡振动峰值
陀螺力矩是造成转子固有频率和临界转频存在差异的主要因素,而转动惯量是影响陀螺力矩的内在因素[21]。双转子系统结构中,盘状结构和系统转动惯量较小,陀螺力矩对系统固有频率的影响几乎可以忽略,系统固有频率与其临界转频基本相等,故系统在其固有频率处会发生共振,出现振动峰值。
由图6a及表2可知:电磁轴承支承刚度为1×105N/m时,系统在内、外转子混合激发的前4阶模态频率(19,23,57,83 Hz)处出现振动峰值,当电磁轴承支承刚度从1×105N/m增加到4×106N/m时,系统前4阶共振频率增大,进而使原共振频率处的振幅减小,可见内转子在内、外转子混合激发的模态处的不平衡响应是可控的;电磁轴承支承刚度为4×106N/m时,系统在外转子激发的3,4阶模态频率(128,164 Hz)处出现振动峰值,当电磁轴承支承刚度从4×106N/m增加到1×107N/m时,系统3,4阶共振频率增大,进而使原共振频率处的振幅减小,可见内转子在外转子激发的模态处的不平衡响应是可控的;电磁轴承支承刚度为4×106N/m时,系统在内转子激发的刚性模态频率(51,75 Hz)处出现振动峰值,电磁轴承支承刚度从4×106N/m增加到1×107N/m时,系统在这2处的峰值频率及大小均不发生变化,可见内转子在内转子激发的刚性模态处的不平衡响应是不可控的;电磁轴承支承刚度为1×105N/m时,系统在内转子激发的柔性模态频率(229,589 Hz)处出现振动峰值,电磁轴承支承刚度从1×105N/m增加到1×107N/m时,系统在这2处的峰值频率及峰值均不发生变化,可见内转子在内转子激发的柔性模态处的不平衡响应是不可控的。
同理,由图6b可知:外转子在内、外转子混合激发的前4阶模态频率(19,23,57,83 Hz)附近的共振频率随电磁轴承支承刚度增大而增大,进而使原共振频率处的振幅减小,其不平衡响应是可控的;外转子盘在外转子激发的3,4阶模态频率(128,164 Hz)附近的共振频率随电磁轴承支承刚度增大而增大,进而使原共振频率处的振幅减小,其不平衡响应是可控的;外转子盘在内转子激发的刚性模态频率(51,75 Hz)附近的不平衡振动峰值频率不随电磁轴承支承刚度变化,但峰值大小随电磁轴承支承刚度增大而减小,故其不平衡响应亦可控;外转子盘在内转子激发的柔性模态频率(229,589 Hz)附近的不平衡振动峰值大小及频率均不随电磁轴承支承刚度变化,其不平衡响应是不可控的。
综上所述,当永磁中介轴承支承刚度一定时,双转子系统中外转子激发或内、外转子混合激发的模态不平衡振动是可控的,与系统模态分析一致。不平衡响应分析可判断内转子激发的模态的可控性:内转子激发的柔性模态不平衡振动是不可控的;内转子激发的刚性模态不平衡振动不可控,外转子上的不平衡振动可控。
3 结论
1)根据内、外转子独立模态是否与磁悬浮双转子模态相同,可将系统模态按激发状态分为3类:内转子激发,外转子激发及内、外转子混合激发。
2)系统中内转子激发的模态固有频率不随电磁轴承支承刚度发生变化,外转子激发或内、外转子混合激发的模态固有频率随电磁轴承支承刚度增大而增大。系统中外转子激发或内、外转子混合激发的模态,内、外转子不平衡振动均可控。
3)内转子激发模态的固有频率不随电磁轴承支承刚度变化;但若模态为刚性,则外转子不平衡振动的峰值随电磁轴承支承刚度增大而减小,内转子不平衡振动峰值不变;若模态为柔性,则内、外转子不平衡振动的峰值均不发生变化。内转子激发的刚性模态,外转子不平衡振动可控,内转子不平衡振动不可控;内转子激发的柔性模态,内、外转子不平衡振动均不可控。
