复杂地质大直径盾构隧道列车振动响应分析

王爱武，蒋 超，戴志成，方若全

(1.广东珠三角城际轨道交通有限公司，广州 510230； 2.中铁第四勘察设计院集团有限公司，武汉 430063； 3.西南交通大学交通隧道工程教育部重点实验室，成都 610031)

引言

盾构法施工因其自动化程度高、安全高效、对地层扰动小等优点，逐渐成为城市地铁隧道及跨海越江隧道施工的首选工法[1]。伴随高速铁路的快速发展，高速列车荷载对盾构隧道结构的影响逐渐受到学者们的广泛关注[2]，同时越来越多铁路穿越软土或软岩等软弱地基，由此引起的基底累积塑性沉降问题日益突出[3-4]。

针对列车振动对盾构隧道结构的影响，张玉娥、白宝鸿[5]通过现场测试的方法，得到轨道振动加速度的数学公式，建立了车辆轮系运动方程，从而推导出列车振动荷载。丁祖德等[6]建立隧道-围岩相互作用的动力有限差分计算模型，研究了列车运行速度、围岩条件、隧道底部结构厚度以及基底软弱层厚度的不同对列车振动荷载作用下的铁路隧道的结构动力响应特征。李亮等[7]运用弹塑性有限元方法，就不同断面形式、车速和阻尼比系数等因素，对大断面隧道结构在列车振动荷载作用下的动响应进行了深入的对比分析。此外，刘建达等[8]采用ABAQUS软件，以南京地铁沿线典型场地条件为研究对象，采用修正Martin-Seed-Davidenkov动黏弹塑性本构分析了地铁列车运行引起的地表振动特性。孙晓静[9]以北京地铁4号线为背景，采用理论分析、现场测试、数值模拟及原型试验等多种研究方法，完成了地铁振动现状的测试与分析、隧道/地层系统振动特性分析、地表振动响应预测分析、轨道减振性能研究分析、环境振动影响分析等多项工作。高峰等[10]依托深圳地铁某近距离重叠隧道工程，研究了列车振动对既有隧道结构的影响。

针对列车振动对盾构隧道基底土体动力性状和累计变形，徐庆元等[11-12]基于车轨耦合动力学理论，建立列车-无砟轨道-路基非线性耦合模型，对路基不均匀沉降问题进行了研究。施成华等[13]采用动力有限元数值方法，对某隧道典型砂层段进行动力响应分析，探讨了列车长期荷载作用下隧道基底砂层累计变形计算方法。张小会等[14]推导了板式轨道在考虑自重情况下的结构振动方程，建立相应耦合分析模型，研究不同速度、沉降度下系统动力响应的影响。

然而目前在列车速度显著提高条件下，研究长期循环动载对隧道结构及其周围环境影响的现场测试受限较多，同时列车振动荷载对复杂地质条件下大直径盾构隧道影响的研究较少。因此通过有限元方法，以佛莞城际狮子洋隧道工程为对象，选取典型软硬不均地层，分析隧道结构动力响应特征、地基土的沉降特性，讨论盾构隧道结构安全性问题。

1 工程背景

佛莞城际铁路为珠三角城际轨道交通东西向主动脉的组成部分，西起广佛环线上的广州南站，经长隆、番禺大道、官桥、莲花后过珠江狮子洋进入东莞境内，设麻涌站后，接入望洪站。其中下穿珠江口狮子洋段的狮子洋隧道全长6.15 km，连接番禺石楼镇及东莞麻涌镇，为全线重点控制性工程。隧道处于极为复杂的软硬交替性复合地层，横断面采用单洞双线设计，管片外径13.1 m，厚度550 mm，隧道行车速度目标值200 km/h，是国内又一座大断面、高难度、高风险的城际铁路水下隧道。见图1。

图1 佛莞城际铁路狮子洋隧道纵断面

2 数值分析

2.1 列车荷载的确定

确定列车荷载的方法一般有现场实测和经验公式模拟。经验公式法无法真实反映列车及轨道情况，因此结合列车-轨道系统动力分析模型与相关实测结果[15-16]，获取作用于道床底部的列车荷载时程曲线，作为动力荷载作用施加在隧道左、右轨道基底进行列车振动响应分析。施加的列车荷载如图2所示。

2.2 基本假设

模型基本假设：(1)隧道结构沿纵向无变形，土-结构体系符合平面应变的假定；近似认为局部波场为平面波系，故可利用平面分析得出体系的基本波动特性。地下结构材料简化为均质各向同性弹塑性体；(2)动力作用下，土体与结构之间、土层之间、不存在相对滑动、脱离，界面满足位移协调条件；(3)采用总应力分析法，未考虑孔隙水压变化对结果的影响。

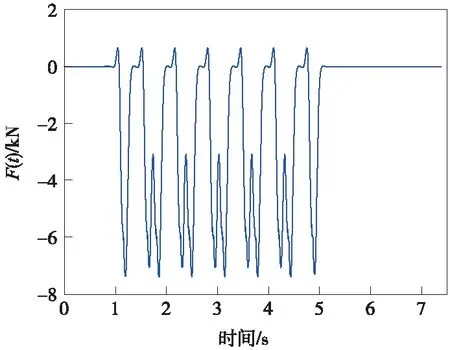
图2 v=200 km/h时的列车振动荷载时程曲线

基于上述假设，采用ANSYS瞬态动力学模块进行动力分析。采用Plane42单元模拟土体和隧道内部基底板及立柱，采用Beam3单元模拟衬砌。其中，土体采用弹塑性模型模拟，混凝土采用弹性模型。基底和衬砌采用C50混凝土，隧道等效直径12.55 m(外径13.1 m，内径12 m)，衬砌厚度550 mm，模型长度方向取160 m，深度方向根据埋深确定，模型如图3所示。

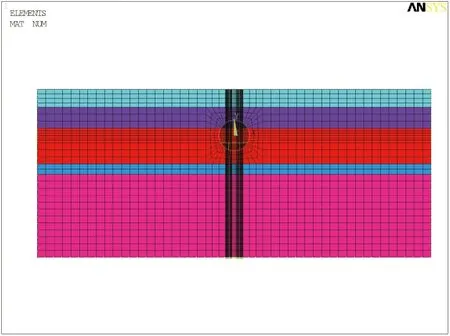
图3 整体模型

2.3 阻尼及积分步长的确定

用有限元法在时域内求解动力问题，必须保证计算过程的稳定性。时间步距Δt若选取过大，将损失高频成分，使精度降低，严重时导致计算发散。时间步长选取过小，则耗费机时，且累积误差也将影响计算精度。

Δt应该小到波在单元之间传播时足以捕捉到波动效应。因此时间步长应为

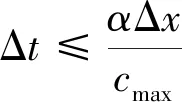
(1)

式中，Δx为传播方向的最小网格尺寸；cmax为传播波速的最大值；经验系数一般取1/3。

研究表明：为了保持计算的足够精度，时间步长不应该大于系统的最大固有周期的1/100，即时间步长为

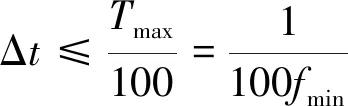
(2)

式中，Tmax为系统最大固有周期；fmin为响应最小固有频率。

在ANSYS的瞬态动力学分析中，可以指定Rayleigh阻尼中的Alpha阻尼和Beta阻尼。通常α和β的值是用振型阻尼比ξi计算出来的。如果ωi是第i阶模态的固有频率，根据振型正交条件，α和β与振型阻尼比之间应满足以下关系式

ξi=α/2ωi+βωi/2

(3)

为了确定某一给定阻尼比ξi的α和β值，可假定ξi在某个频率范围(ωi，ωk) 内近似为恒定值，则有

(4)

阻尼系数α和β需通过结构的某一振型的阻尼比和频率来确定。在动力分析中，由于结构前几阶振型起主要作用，故采用结构的前几阶振型频率与结构的临界阻尼比确定瑞利阻尼系数。

在对围岩-隧道体系进行模态分析时，ANSYS提供了6种提取模态的方法。对于阻尼不可忽略的问题，需采用Damped法，但在此处讨论体系的固有特性时，由于阻尼对固有特性的影响很小，因此可按无阻尼系统进行模态分析。本文采用Block Lanezos法，提取前8阶模态，对应的频率见表1。材料阻尼采用Rayleigh线性阻尼，取Δt=0.005 s，而围岩的阻尼比取ξ=0.05[17]，计算前两阶模态的频率，即可求得断面一的阻尼常数α=0.083 87，β=0.029 28；同理断面二的阻尼常数α=0.095 03，β=0.025 77。

体系最大固有周期为Tmax=1/fmin=4.46 s，为了保持计算的精度，隐式积分的时间步长不应该大于该值的1/100，所以Δtmax<0.044 6 s，实际采用的计算时间步长为Δt=0.005 s。

表1 断面一模态分析结果频率

2.4 计算工况

本隧道为国内首例全断面穿越复合地层的城际铁路水下盾构隧道，存在全断面软弱地层(砂层、淤泥两种)、上软下硬(土岩复合)、全断面岩层、破碎带等复杂地质条件，而对于流塑性淤泥层和透水砂层，高速列车往复振动引起长期沉降可能较为显著。鉴于此，选择JzIII-13狮子洋钻孔位置28号(隧道地基为流塑性淤泥层)和149号(隧道地基为透水砂层)位置作为计算断面，由于列车振动响应分析时，两断面规律相似，只列出前者计算结果。考虑软弱岩层、深厚淤泥层地质地基在往复荷载作用下的累计沉降问题时，则同时分析两断面计算结果。

佛莞城际铁路狮子洋隧道作为单洞双线隧道，相比一般的单线隧道具有两车交汇的特殊性，应考虑列车行进时交汇的时间间隔以及列车的速度，分别取间隔时间为1 s和2 s进行分析，并考虑两条轨道仅有一列车通过的情况，并取列车设计速度200 km/h作为计算速度，考虑对称性，只需要计算左侧或右侧列车单独通过或提前0.5，1.5 s时的情况，则计算的工况如表2所示。

表2 计算分析工况

3 计算结果与分析

3.1 列车振动隧道结构响应分析

动力求解建立在静力分析、开挖和支护后形成稳定应力场之后，横断面响应主要包括地层的动力响应分析和结构的动力响应分析。结构动力响应分析包括衬砌的主应力、位移、加速度随时间的变化。主要选取拱顶、拱底及柱与路板的交点进行结构动力响应分析，并取地层中不同深度的点进行地层动力响应分析，计算提取参考点如图4、图5所示。

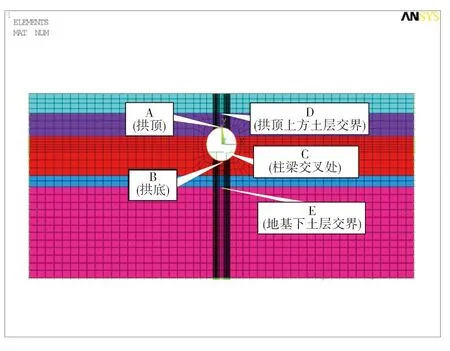
图4 断面1结构响应分析点示意

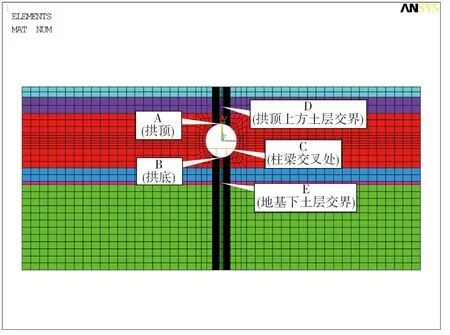
图5 断面2结构响应分析点示意

(1)结构振动响应分析

模型整体自振3 s以完成自重的加载和稳定，列车振动荷载从t=3.005 s开始施加，振动时间为一个列车通过历程。为了让模型稳定，在动荷载施加之后，再自振1 s，分别提取拱顶、拱底、柱梁交界的位移时程，工况1～工况3下拱顶位移曲线如图6、图7所示。

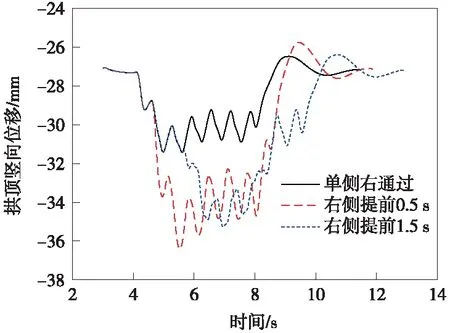
图6 拱顶竖向位移时程曲线

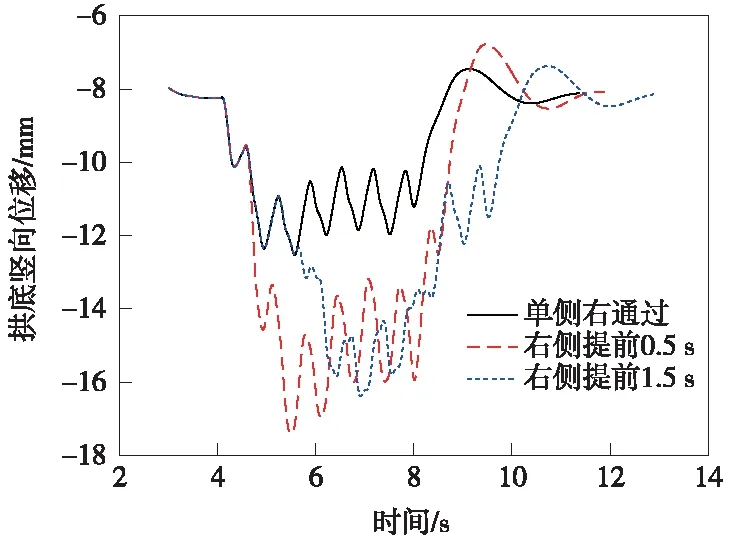
图7 拱底竖向位移时程曲线

在软土地层中，列车振动荷载产生的结构响应基本类似，即在前4s，振动位移无显著变化，随着列车的驶入，位移不断增加，呈波动变化；随着列车的远离而位移逐渐恢复平静。拱顶的位移比拱底和梁柱交界处的位移稍大，位移均表现下沉，单侧通过和右侧提前有明显的位移振幅偏移现象，即位移最大值出现时间偏移量跟提前的时间大致相同，右侧提前0.5s时，位移较其他二者大。

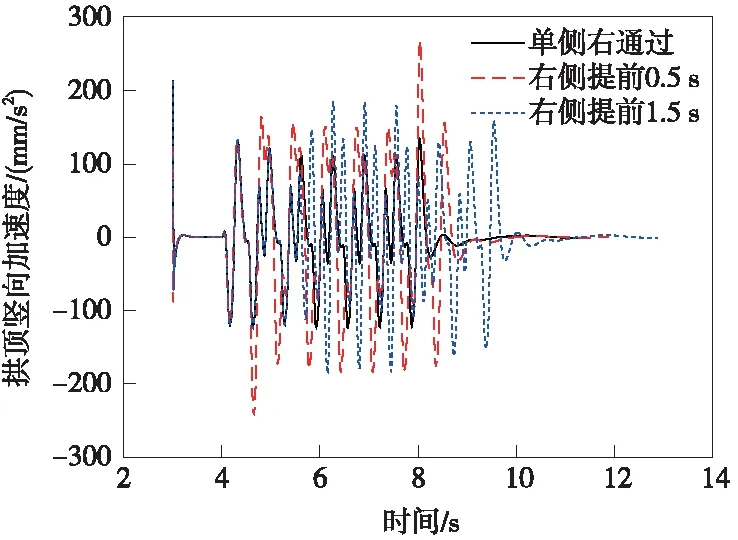
图8 拱顶竖向加速度时程曲线

列车振动产生的加速度变化基本类似，从竖向加速度时程曲线(图8)可以看出，一般从第4 s开始迅速变化，呈周期性波动，到11 s后基本停止振动，右侧提前0.5 s的振动幅值最大，这是由于两车间隔时间短，荷载叠加效应所致，提前的时间跟最后波动恢复平静的时间延误大致相同。

为了分析结构的受力变化，提取拱顶、拱底和梁柱交界节点的主应力进行分析，包括第一主应力和第三主应力，以研究结构的安全性能，如图9～图11所示。

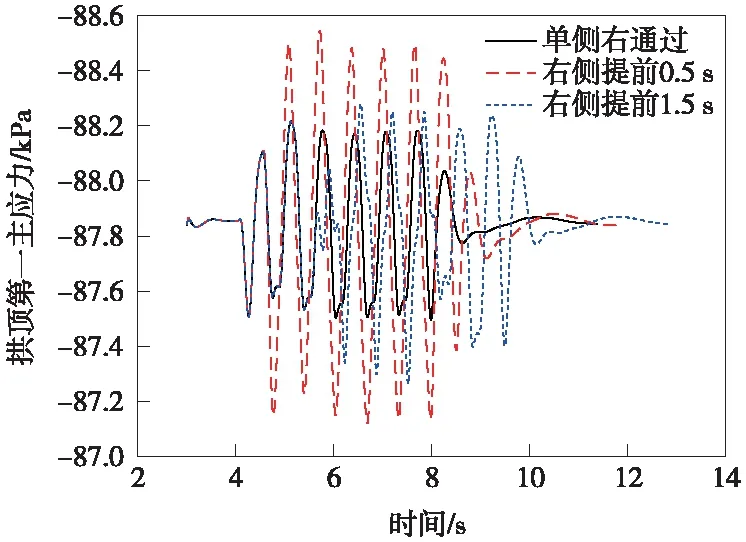
图9 拱顶第一主应力时程曲线

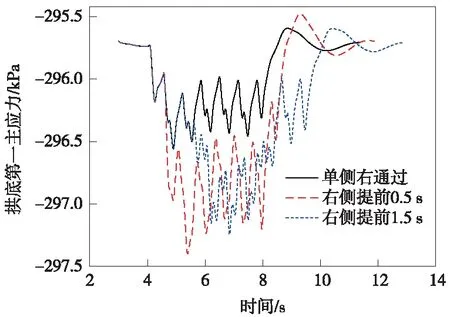
图10 拱底第一主应力时程曲线

结构在拱顶和拱底的第一主应力随时间的变化并不明显，一般幅值相差在2 kPa以内，梁柱交界处的第一主应力不变，主要是结构的对称性和Link单元和梁单元的受力特性所致，说明主应力的变化不明显，基本不影响结构的受力；时间提前也会造成主应力的波动往后偏移相同的提前量，提前0.5 s由于叠加效应幅值变化更为明显。

结构第三主应力的变化跟第一主应力的变化规律基本相同，但相比第一主应力而言，(负)值有所增加，二者最大幅值出现的位置和波动平息的时间基本一致，且梁柱交界处的第三主应力也基本不变。

图11 梁柱交界处第一主应力时程曲线

3.2 列车往复荷载作用下隧道地基累积变形分析

为了预测反复荷载作用下地基土的累积应变，自1975年以来很多学者提出并完善了相关计算理论与模型。为了对佛莞城际铁路狮子洋隧道典型软土层及砂层在列车往复荷载作用下的累积塑性变形进行计算，本研究主要采用Anand J.Puppala和DingQing Li计算模型[18-20]，相关计算参数如表3所示。为了方便计算，本文中圆砾土和粗砾砂参数相同。

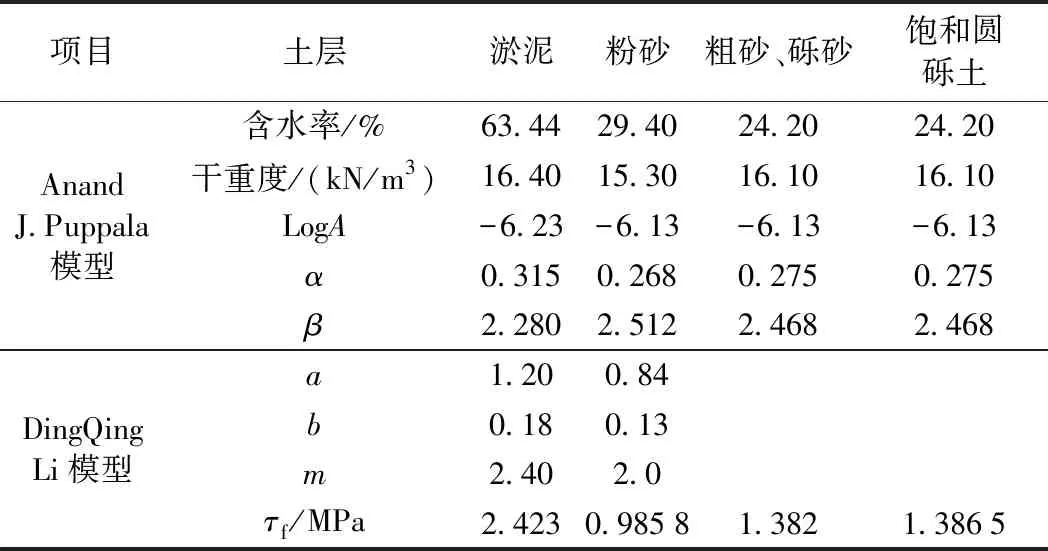
表3 计算参数

列车循环荷载作用下，按两模型计算，得到JzIII-13狮子洋钻孔位置28号经列车作用不同次数后，累积沉降变形值随循环振次的关系如图12所示。

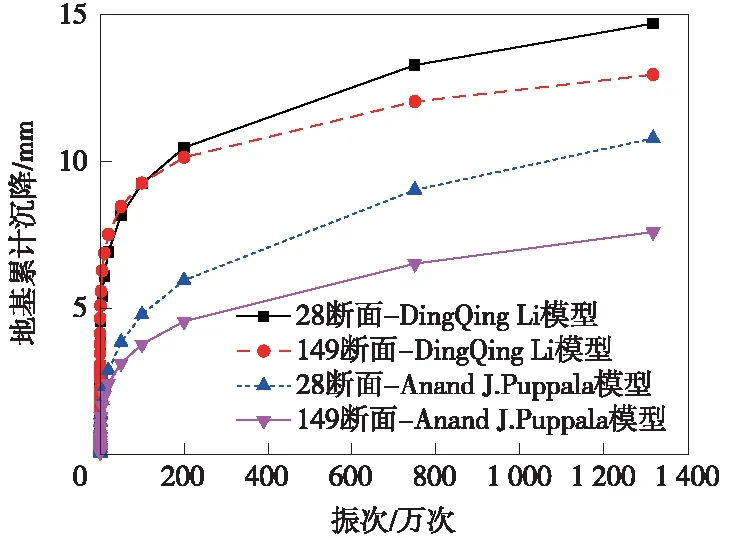
图12 塑性累积变形与循环振次的关系曲线

由计算可得如下结论。

(1)采用Anand J.Puppala和DingQing Li模型进行计算，在隧道运营期达100年时(相当于列车运行1 317.65万次)，28号断面的塑性累积变形分别为10.78 mm和14.70 mm，而149号断面的塑性累积变形分别为7.59 mm和12.95 mm；总体来说，淤泥地层后期累计变形较大。

(2)通过进一步分析可知，28号断面隧道基底有一层约5.35 m左右的淤泥层，JzIII-13狮子洋钻孔位置149号断面隧道基底有一层厚为6.4 m左右的砂土层，而隧道基底的累积塑性累积变形主要是由淤泥层引起的，所以不管是采用Anand J.Puppala模型还是DingQing Li模型，28号断面的累计变形都要大于149号断面。

(3)随着列车运行次数的增加，隧道基底地基土的累积变形逐渐增大，但在列车运行初期基底变形增加较快，但列车运行约1年(约6.5万次)后，隧道基底地基土的累积塑性变形达到总变形值的一半左右，后期隧道地基土的累积变形增加速度明显减慢，对列车运行的影响也逐渐减弱；断面一的后期地基变形增速要大于断面2，表明列车振动的沉降影响在淤泥层中持续时间更长。

(4)因为Anand J.Puppala、DingQing Li两种计算模型考虑应力因素影响不同，适用的地层也不同，根据工程经验与本文计算结果对比发现，Anand J.Puppala模型更适用于砂土层，DingQing Li模型则更适用于淤泥层。而佛莞狮子洋隧道近东莞侧基底以砂土为主，建议采用Anand J.Puppala模型进行沉降计算；佛莞城际铁路狮子洋隧道近广州侧基底以淤泥为主，建议采用DingQing Li模型进行沉降计算。

4 结论

本文研究了大断面盾构隧道复杂地质条件下典型断面的平面振动响应分析和列车反复荷载作用下地基的累积变形，主要结论如下。

(1)对于列车振动产生的动力响应幅值，单次交汇<右侧提前1.5 s<右侧提前0.5 s，说明两股道同时有列车荷载时，产生的动力响应更为显著，且与两车间隔的时间有关，当间隔时间为振动周期的倍数时，振动效应最大，这是波的叠加所致。

(2)列车振动在右侧提前Δt的时间内，响应的振动时程曲线会产生约等于Δt的偏移现象，且振动幅值也会偏移，结构的动力响应与地层的动力响应(位移、加速度和主应力)存在相似的变化规律。

(3)列车振动(包括单次和多次交汇)，对隧道位移和加速度的影响较为明显，而对主应力的影响不明显，最大位移波动幅值可达10 mm，最大加速度波动幅值可达0.5 mm/s2。

(4)在列车长期荷载作用后(相对于隧道运营100年)，通过两种计算模型得到的典型断面基底地基土的累积塑性变形均小于TB10623—2014《城际铁路设计规范》规定的允许最大沉降15 mm，能够满足高速列车长期运营对轨道平顺度的要求，鉴于28号钻孔计算所得最大沉降为14.7 mm，接近规范限值，从安全性考虑，后期将研究控制后期沉降的措施，以确保铁路运营安全。