桩承式路堤土拱效应形成机制离散元模拟

马一跃，吕玺琳，黄茂松

(1.同济大学岩土及地下工程教育部重点实验室，上海 200092； 2.同济大学地下建筑与工程系，上海 200092)

引言

为满足现代交通工具(如高速列车)的严格变形控制要求，桩承式路堤在我国软土地区路基处理中得到了广泛应用。桩承式路堤中，刚性桩的存在改善了路基承载性状，使其能有效控制沉降量[1-2]。弄清桩承式路堤中桩-土相对位移引起的土拱效应，是开展桩承式路堤设计的关键。

自太沙基[3]发现土拱效应以来，已有大量物理模型试验[4-5]和理论分析成果[7-9]。为简化所分析的问题，以往大多数研究从二维角度开展，且在理论研究中常需引入一定假设。经典的Trapdoor试验是研究土拱效应的常见方法，研究结果表明，只要活动板有略微下降，桩间土上的应力便急剧下降。如Chevalier等[10]和Moradi等[5]通过开展Trapdoor模型试验，发现沉降板下沉0.5 mm时桩间土压力就已经骤降到最小值。Chen等[11]通过桩承式路堤土拱效应模型试验分析发现，当桩间土下降约6 mm时达到最小值并趋于稳定。随着计算机的发展，离散元数值模拟方法也被用于土拱效应分析[12-13]，获得了土拱效应发展的细观规律，但目前有关三维离散元模拟的研维角度分析，其土拱形成过程及荷载传递的细观机制还有必要开展进一步研究。

首先建立了二维离散元模型对桩承式路堤中土拱效应进行分析，研究了桩承式路堤桩帽和桩间土压力的发展规律。进一步建立三维分析模型，通过分析颗粒移动趋势，获得了桩承路堤三维非均匀沉降分布。通过对比，揭示了土拱形成过程三维效应对桩顶与桩间土压力变化及荷载传递效率的影响。

1 离散元模型的建立

以无土工格栅的桩承式路堤为研究对象，根据高铁路基的典型值[14]，桩间距设为1.2 m，桩帽宽1.7 m，桩净距为0.5 m。根据以往平面应变土拱效应分析可知，只有填土高度达到1.6倍桩净距以上，土拱效应才能完全发挥。因此，路堤填土高度最小选为1.0 m，另增加1.25，1.5 m的情况分析填土高度的影响。通过PFC2D软件，构建了二维土拱模型，两侧底部不动墙模拟桩，考虑对称性尺寸为桩帽的一半即0.35 m，中间设置沉降板宽0.5 m。该模型类似于传统的Trapdoor试验，如图1(a)所示。考虑到桩的对称性，取桩帽的1/4进行分析，建立的三维土拱离散元模型如图1 (b)所示。

图1 离散元模型

DEM模型中颗粒选用级配较好的丰浦砂作为研究对象，为减小模型中颗粒生成数量，提高离散元模型计算效率，将丰浦砂的级配放大70倍(图2)。为尽量真实地反应填料的力学性能，二维和三维离散元模型中的颗粒均采用了抗转动模型，二维离散元模型的细观参数根据文献[15]选取，三维离散元模型则参考文献[16]，具体采用的细观参数见表1。为生成均匀的离散元模型，模型生成时采用了分层压实法[17]，赋予颗粒1倍的重力加速度通过重力沉积法使模型达到稳定。模型生成完后，使模型中的沉降板以0.003 m/s的速度下降。

图2 离散元模型中的颗粒级配

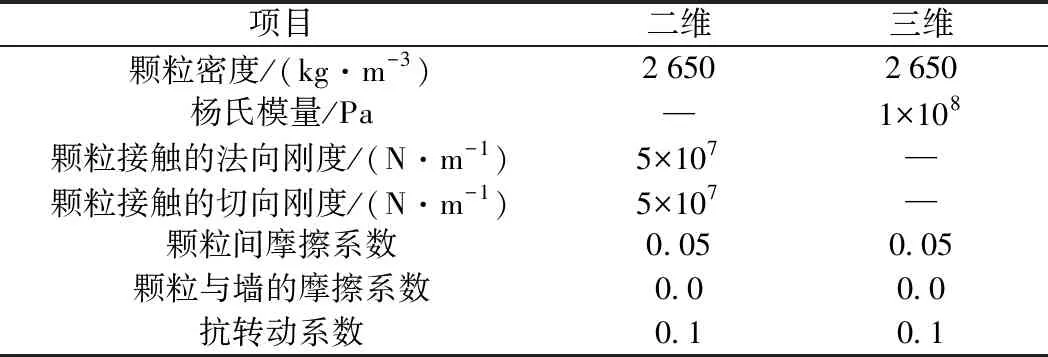
表1 数值模型中的细观参数

2 二维条件下的土拱效应

2.1 桩土应力变化规律

受土拱效应影响，二维土拱模型中桩顶土压力随着桩-土相对位移Δs增加而增加，桩间土压力则随着Δs增加而减小。当Δs=3 mm时，压力便达到稳定值(图3(a))，且填土高度越大，两者土压力越大，这与Chen等[9]的结果相似。

为进一步分析土拱效应中荷载传递效率，引入如下荷载传递效率比进行分析。

(1)

式中，Fp和Fs分别为作用在桩帽和桩间土的力。

二维土拱模型中荷载传递效率E均随填土高度增加而增大，变化过程如图3(b)所示。填土高度对荷载传递效率影响较小，稳定值约为78%。

图3 不同填土高度下桩顶/桩间土压力和荷载传递效率随差异沉降的变化

2.2 颗粒位移和力链变化

在沉降板下降到12.5 mm时，二维土拱模型颗粒位移分布如图4(a)所示。根据颗粒位移分布，3个模型均产生了半椭圆形土拱。h填土为1.25 m和1.5 m时，土拱高度均为0.4 m，等于0.8倍桩净距(0.5 m)；h填土=1.0 m时，相应的土拱高度约为0.5 m，等于1倍的桩净距，说明填土高度的增加有助于土拱形成，该结论与Lai 等[12]得到的结果一致。3个模型中土体沉降分布规律表明，h填土=1.5 m的模型中填土高度超过0.4 m(土拱高度)后，表层土体表现为均匀沉降；相反h填土=1.0 m和1.25 m的模型中超过土拱高度的颗粒，依然存在不均匀沉降。

颗粒的位移矢量图(图4(b))进一步表明了不同填土高度下的颗粒移动趋势。在h填土=1.5 m条件下，超过土拱高度颗粒的位移减小且均垂直向下均匀下沉；在h填土=1.25 m和1.0 m模型中，超过土拱高度依然存在位移较大的颗粒，尤其是h填土=1.0 m时，形成了类似顶部开口的半椭圆形状。颗粒间力链的分布能充分展示土拱效应的荷载传递机制，根据数值模拟得到的力链分布如图4(c)所示。桩顶处应力高于两侧，且随高度增加而衰减；沉降板上部拱形范围内力链内旋，主应力链逐步构成拱门状。

图4 不同填土高度条件下二维土拱模型沉降和力链分布(Δs=12.5 mm)

2.3 不均匀沉降分布规律

根据图4(a)中颗粒的位移图，分析二维土拱模型中不同填土高度(H)处土体的不均匀沉降值，如图5所示。3个模型在H=0.25 m处土体的不均匀沉降均呈“V”形分布，土体沉降值从中间向两侧逐渐减小。h填土=1.5 m模型中，H≥0.5 m处的土体不均匀沉降曲线近似于一条直线，说明未发生不均匀沉降。当h填土=1.25 m和1.0 m时，随着H增加，“V”形倾斜度逐渐减小并转变为一条下凹曲线，桩上部土体不均匀沉降值随着H增加而增加，与沉降板上部土体沉降值相反。这说明当路堤填土高度与桩净距之比达到2.5=1.25 m/0.5 m时，在顶部依然存在不均匀沉降。

图5 不同填土高度条件下二维土拱模型不均匀沉降

3 土拱效应三维效应

3.1 桩土压力变化规律

相对于二维土拱模型，三维土拱模型中桩顶土压力增加和桩间土压力减小的速率明显减小，当Δs≈130 mm时才达到稳定，且填土高度越大达到稳定时所需的桩-土差异沉降也越大。受土拱效应影响，三维土拱模型中h填土=1.0 m的桩顶土压力增长速率明显大于h填土=1.5 m和1.25 m，桩间土压力的下降趋势也更明显，如图6(a)所示。

三维土拱模型中，填土高度对荷载传递效率E的影响也相对较大，h填土=1.5 m和1.25 m时，E的稳定值约为68%，而h填土=1.0 m时只有57%，且明显小于二维土拱模型，如图6(b)所示。这主要是由于二维土拱模型只能反映两根桩之间的土拱效应造成的，桩间土压力也只考虑了平行桩之间的土体忽略了斜对角桩之间的土体。然而，三维情况下每个桩分别会与其余附近的桩共同产生土拱效应，类似于图6(b)中的Ⅰ、Ⅱ、Ⅲ号虚线。以此说明，二维土拱模型高估了荷载传递的效率。

图6 不同填土高度中桩顶和桩间土压力的变化

3.2 颗粒位移分布规律

三维土拱模型中，当沉降板下降达到130 mm以后桩顶土压力达到稳定状态。取沉降值达到135 mm处不同填土高度下颗粒的位移，如图7所示。从侧面观察到的三维模型中颗粒位移趋势与二维土拱基本相似，这主要是由于该处的土拱主要受两个平行桩的影响造成的。三维土拱高度与二维土拱模型略有不同，h填土=1.5 m时，由土体沉降形成的半椭圆形土拱高度为0.44 m，略大于0.8倍桩净距。h填土=1.0 m时，顶部存在下凹的不均匀沉降面，半椭圆土拱高度为0.35 m，明显小于二维土拱模型得到的结果，这反映了三维土拱模型中桩间土的分布与二维土拱模型的差异。

图7 不同填土高度三维土拱效应模型中颗粒的沉降(Δs=135 mm)

4 结论

通过对Trapdoor试验离散元模拟，从二维和三维角度对桩土差异沉降引起的土拱效应形成机制荷载传递过程进行分析，主要得到以下结论。

(1)相对于二维土拱模型，三维情况下桩顶与桩间土的土压力需要较大桩-土差异沉降才能达到稳定，荷载传递效率受填土高度影响更大。二维土拱模型高估了荷载传递的效率，即二维土拱模型只能够反映两根桩之间的荷载传递机制，而实际工程中单根桩会与周围其他多根桩共同形成荷载传递效应。

(2)二维和三维土拱中均呈现出半椭圆形土拱，当路堤填土高度达到一定值时，其高度约为0.8倍的桩净距。在二维土拱模型中，不同高度处的填土的不均匀沉降呈“V”形。