火箭助推载重滑翔机模型设计与实践研究

张家苇，蔡杭城，卢洋洋，姜凤华，沈一军，刘子振

（台州学院 建筑工程学院，浙江 台州 318000）

0 引言

浙江省大学生力学竞赛主要培养大学生的创新思维和实践动手能力，激发大学生学习力学及相关专业知识的热情，促进浙江省高校大学生相互交流与提高。2017年的浙江省第六届大学生力学竞赛以“火箭助推载重滑翔机设计制作与飞行”为主题，设计并制作火箭助推条件下具有载重能力的滑翔机，竞赛内容包括以下环节：理论方案设计、模型加工制作、飞行试验和答辩。竞赛评判的关键点如下：

（1）载重物必须安装在滑翔机上，随滑翔机起飞和降落。载重物和滑翔机应单独的进行质量审核，审核完成后现场进行载荷安装和固定。安装和固定载荷的过程中不允许再对滑翔机和载荷进行任何减轻重量的处理和加工。飞行过程中不允许载荷物脱离滑翔机。

（2）滑翔机空载状态下总质量应不小于25 g，配重块质量应为：5 g≤mp≤30 g，模型飞行时的最大翼展为480 mm-550 mm。

（3）滑翔机主要尺寸和理论方案设计尺寸的误差应在5%以内。

（4）模型正常飞行的综合评判计分方法为：50×（A/Ab），其中 A=mp×t；mp和 t分别为相应的载重量和飞行留空时间。Ab为三个最大A值的算数平均值。

1 滑翔机模型爬升原理分析

1.1 模型爬升的影响

1.1.1 迎角的影响

迎角是指模型相对气流方向与翼弦之间所夹的角度。飞行速度等相同时获得最大升力的迎角称为临界迎角。在小于临界迎角范围内，模型升力随迎角增大而增大；超过临界迎角后，模型升力随迎角增大反而减小。模型阻力随迎角增大也越大，超过临界迎角的阻力急剧增大。

1.1.2 飞行速度和空气密度的影响

模型飞行速度越大相应的升力、阻力也越大。在相同条件下，升力、阻力与飞行速度的平方成正比例。模型的升力和阻力随空气密度增大也增大，升力和阻力与空气密度成正比例。

1.1.3 模型机翼面积、形状的影响

模型的升力和阻力都与机翼面积的大小成正比例。而且机翼形状对升力、阻力也有很大影响，包括机翼切面形状的相对厚度、机翼平面形状、襟翼和前缘翼缝的位置等。另外模型表面光滑程度也会影响到模型的摩擦阻力，表面相对光滑，阻力相对也会较小。

1.2 助推滑行计算

滑翔机模型爬升过程假定是在静气流环境和周围空气不可压缩条件进行分析。滑翔机的飞行性能主要取决于滑翔机的气动性能和稳定性［1-2］，模型助推滑行越高对后续滑翔更为有利，同等条件下飞行留空时间一般越长。模型助推滑行阶段主要依靠火箭提供的推力，火箭推力参数和推力曲线如表1和图1所示。

表1 火箭基本参数表

图1 火箭推力曲线图

根据模型助推滑行的质心动量定理［3］（如图2），可得模型垂直爬升方程：

式中，T为火箭助推力（N），D为空气阻力，t为助推时间（s），m为火箭和模型质量（kg），mp为配重块质量（kg），vc为整体质心速度（m/s），g为重力加速度（m/s2）。

根据相关文献可知空气阻力公式［1］：

式中，CD为空气阻力系数，对机身、机翼和火箭近似取0.18；ρ为空气密度，常温20℃低空取1.205 kg/m3；Aw为最大迎风面积；v为飞行速度（m/s）。

滑翔机与火箭分离后，火箭助推力消失，模型飞行方程为：

式中，m0为火箭的质量。

将式（2）代入式（3），得到滑行阶段的微分方程为：

模型下降单位高度所需时间可按下式计算：

式中，CL为滑翔机的升力系数，CD为滑翔机模型的功率因素，由模型的气动性决定。

2 滑翔机模型设计与优化

2.1 机身优化

通过增加机头处的楔形块，优化了机头的形状，减小模型质量，使其尽可能接近竞赛规则规定的最小质量（25 g）。滑翔机模型设计［4-5］和楔形块详细尺寸如图3所示，滑翔机模型设计实物如图4所示。

助推滑翔机的飞行过程主要包括助推滑行、过渡和滑翔。其中过渡阶段，由于有些情况难以预见，可选择发射方式和可能的时机来处理。在助推阶段，火箭助推结构受力分析如图5所示。

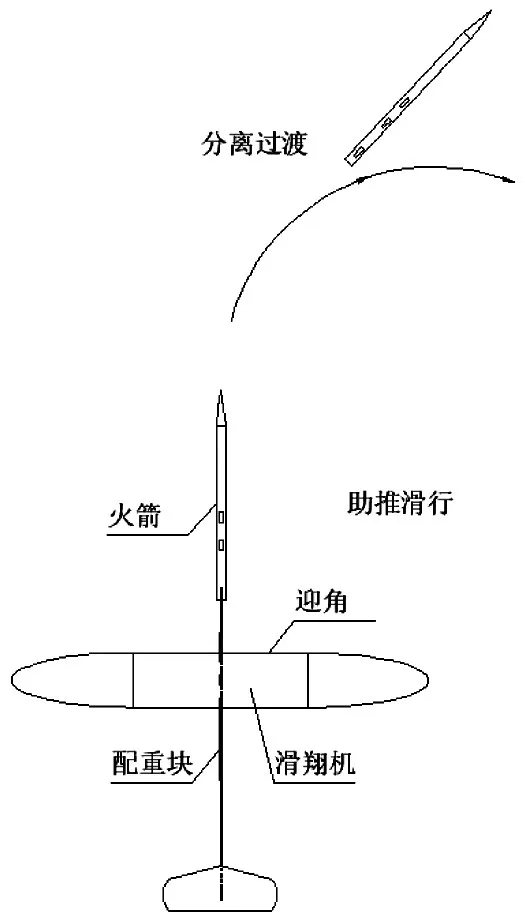
图2 模型助推滑行过程

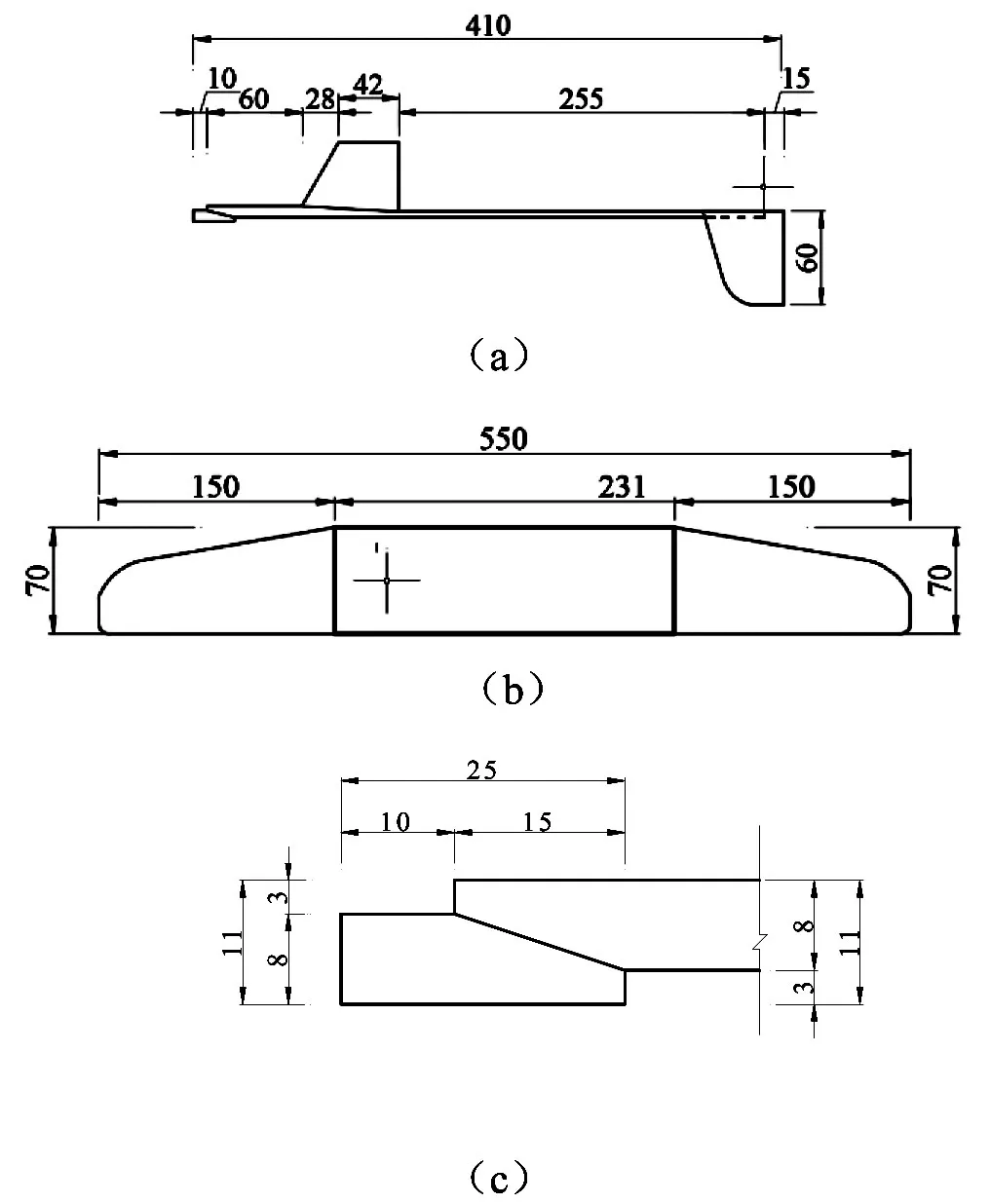
图3 模型设计尺寸详图：（a）机身右视图；（b）机翼；（c）机身楔形块

图4 滑翔机模型图

图5 模型助推阶段平面受力简图

从图中可以看出：（1）减小滑翔机机翼相对于火箭轴线的距离，机翼不会产生大的升力，滑翔机对火箭的扰动会减小；（2）减小火箭推力线与滑翔机重心之间的距离，可以减小助推阶段的俯仰力矩，滑翔机可以爬升的更高，有效提高滑翔机的爬升性能。为了提升滑翔机的爬升性能，应尽量减小重心与火箭推力线的距离。在机身的靠前部位，我们设计一个了楔形块（如图3（c））。楔形块的作用既可使配重块的位置更容易调整，而且发射时滑翔机的重心更贴近火箭推力线。

针对优化后的模型进行了试飞（如表2），对表2进行分析，可得模型重量及重心距机翼前缘位置对飞行时间的影响，如图6、图7所示。

表2 重心位置对飞行时间及状态的影响

图6 模型飞机质量与飞行时间变化图

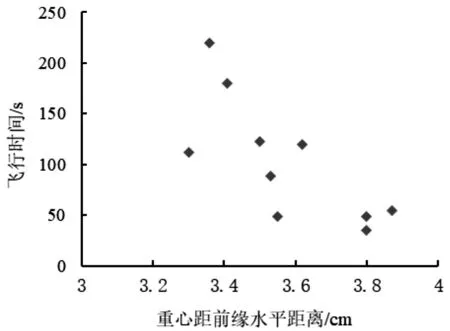
图7 重心距机翼前缘变化下的飞行时间图

由表2和图6可知，模型质量在25 g-26 g之间，飞行状态较好，飞行时间也较理想，因此，模型质量尽量接近最低要求25 g。

由表2和图7可知，模型重心在距机翼前缘3.3 cm-3.5 cm之间飞行状态较好，飞行时间也较理想，故选用此范围作为模型的重心位置。为了减轻机翼质量和减小空气阻力，要对模型的各部件细磨，尽可能光滑，接缝处要仔细处理，务必保证角度准确，粘结牢靠。

2.2 迎角优化分析

方案定好后，针对迎角，我们也对模型进行了数十次试飞试验，试验数据如表3和图8所示，并针对迎角为2.5度时，分析模型质量与飞行时间的关系（如图9）。

表3 迎角对飞行时间及状态的影响

图8 不同迎角下模型飞行时间图

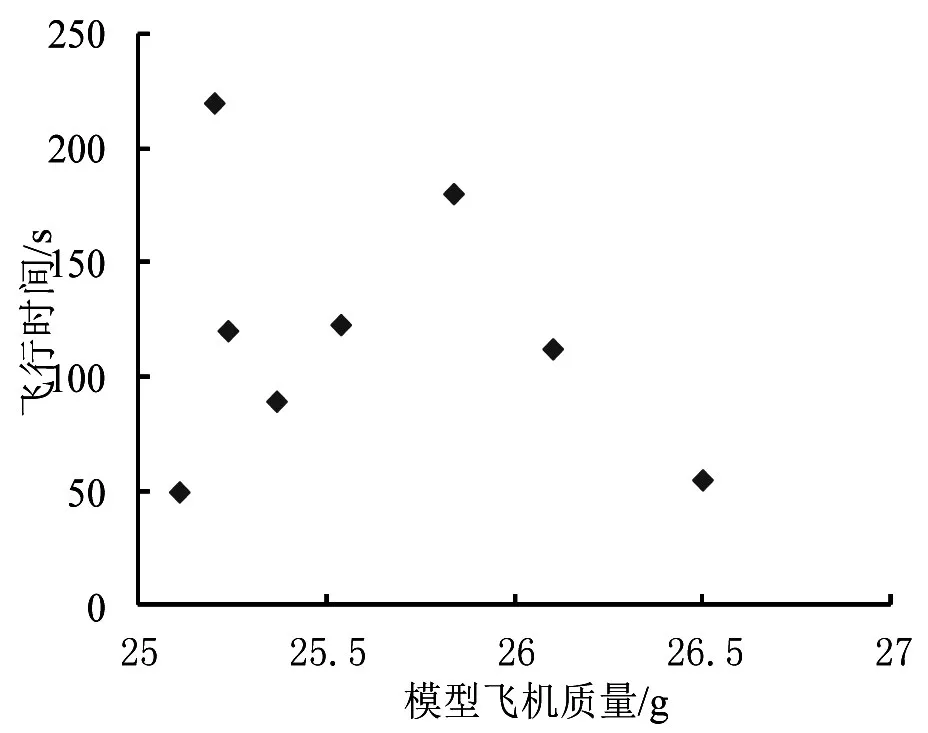
图9 迎角为2.5度下模型质量与飞行时间的关系

通过表3和图8可知，当迎角为2.5度时，飞行状态和时间较为理想，模型有明显滑翔并且滑行时间较长，故本模型最终迎角定为2.5度。

2.3 配重块设计

载重物为组委会定制的专用标准配重块，配重块的设计包括两个方面，第一方面是配重块的配重质量选择（要求最小的配重量为5 g，最大的配重量为30 g）；第二方面是配重块的装配位置的设计，配重块装好后要保证模型重心位置位于压力中心后面，保证模型的升空高度。配重越大，同等条件下爬升高度越低，而模型下降单位高度的时间近似按下式（5）计算。

根据动量定理有

式中，I为火箭总冲量，其它参数同前。

根据式（6）可得，不同配重情况下的助推阶段末速度与质量成反比。

当火箭和模型采用竖向发射时，根据能量守恒，可得

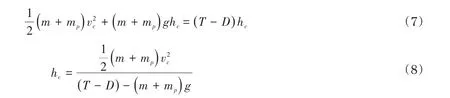
将式（6）代入（8）可得

竞赛提供的发动机总冲为2.85 N·S，平均推力为3 N，在助推阶段若忽略阻力，根据（9）式近似估算模型爬升高度为23 m，速度vc为35.6 m/s。

助推结束到火箭与模型分离时间为1.5 s，若忽略阻力，近似估算模型爬升高度为42 m，最后模型爬升总高度近似估算为65 m。

根据竞赛要求，最优配重质量选取可按照下式进行定性评估，即

将式（5）代入式（10），可得

根据式（11），计算配重质量分别为 5 g、10 g、15 g、20 g、25 g和 30 g的飞行结果分别为：

因此，根据公式（9）和（11）可以定性估算，不同配重情况下爬升高度相差不大，要想达到mp×t最大，飞行时间的要求相差较悬殊，且飞行过程中还有很多不可控因素，因此，对于竞赛提供的发动机型号，选用最大30 g配重综合效果较好。

2.4 模型滑翔时间估算

根据模型的有关气动性能，可得模型滑翔过程的雷诺系数为，

式中，μ为空气粘性系数，近似取1.8×10-5N·s/m2；v为飞行速度（m/s）；d为机翼杆长，本方案d=7 cm。

模型的升阻比为，

式中，C滑翔机的升阻比；vy为滑翔机竖直方向上的飞行速度（m/s）。由于不具备风洞实验条件，因此，采用手掷模型的方法来近似估算模型滑翔速度，实验结果如表4所示。

表4 模型手掷试验数据

由手掷试验可得飞行速度v=5.35 m/s、vy=0.57 m/s，可得模型的升阻比为C=9.39。将以上参数代入式（12），可得 Re=25071。

将空气阻力系数和升阻比代入式（12），，可得滑翔机的升力系数CL=1.69、功率因素为CL3/2/CD=12.21。按式（5），可得模型下降单位高度的时间为1.17 s则滑翔机模型下降飞行时间为76 s。

根据预先定好的优化方案参加竞赛，参赛现场进行模型设计制作和参数设置，滑翔机模型重量为25 g，配重为满载30 g。由于竞赛当天风力较大，竞赛飞行时间仅为55 s，基本符合优化方案的试飞结果，最终获得一等奖。

3 结论

通过试飞试验和手掷模型试验结果，火箭助推载重滑翔机模型主要从以下几方面优化设计：（1）设置迎角为2.5度；（2）在机头处增加契形块，使模型重心定位在距机翼前缘3.3 cm-3.5 cm，改善了飞行状态和时间；（3）模型空载质量应尽可能小，考虑到材料本身质量偏差、天气情况等，模型质量基本控制在25.1 g～26 g之间；（4）通过计算分析确定配重为满载30 g。按照以上方式进行优化设计，滑翔机模型飞行状态较好，飞行时间也较理想。由于滑翔机滑翔过程中，可能会受到水平、垂直或者斜向的突风荷载，因此，还存在不可控因素影响优化方案的结果。