一个关于Carleman不等式的全新加强式

薛睿琪，许呈翔，赵岳清

（台州学院 电子与信息工程学院，浙江 临海 317000）

不等式的研究是数学分析近几百年发展过程中的一个历久弥新的课题.不等式的理论从一开始零星碎片化的研究，到20世纪形成了系统化的理论基础.如今，不等式理论已经是数学分支中不可剥离的一份子.Carleman不等式是乘积幂级数的估计式，为了使该估计式的逼近效果更为显著，后人对Carleman不等式的改进和推广从未停滞.

在1922年，Torsten Carleman给出了一个著名Carleman不等式［1］.

定理1设ak＞0,k=1,2,…,且收敛，则

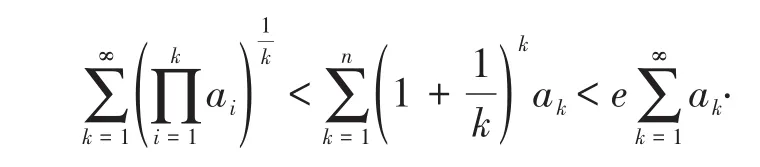
从此以后，对它的研究经久不衰.

2001年，文献［2］对Carleman不等式进行了加强，建立了如下不等式

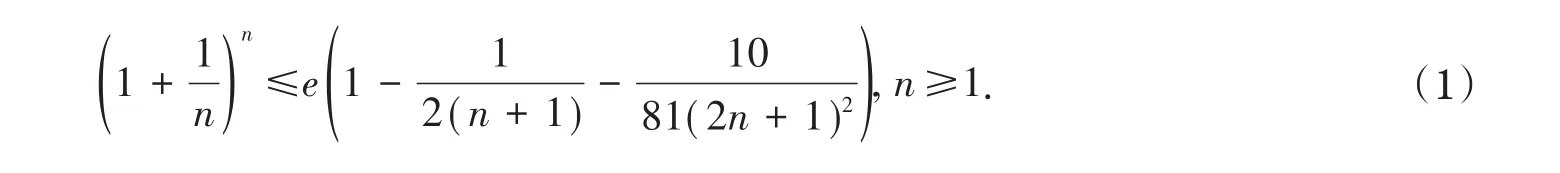
2012年，文献［3］又将Carleman不等式进一步改进如下

1988年，在文献［4］中建立了如下关于常数e的逼近式

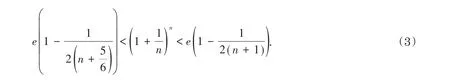
2017年，文献［5］对关于常数e的逼近式进行如下加强，

2005年，文献［6］将Carleman不等式进行如下的进一步优化

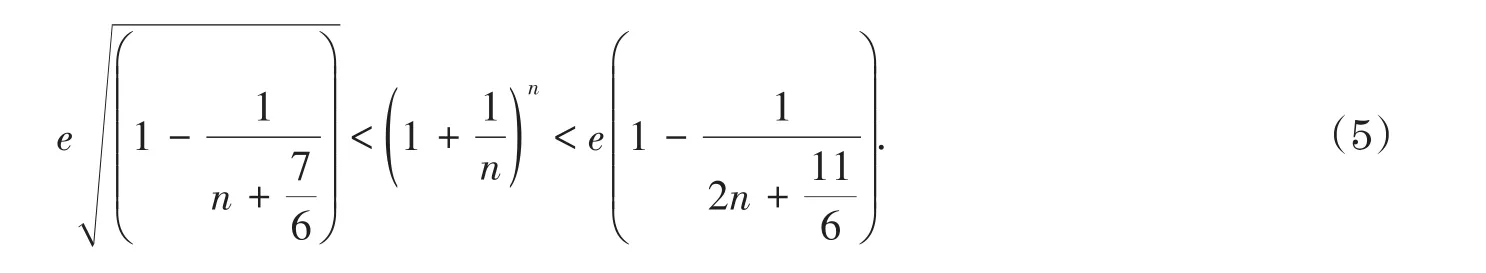
通过此式，给出了如下常数e的多项式逼近的结果

2011年，文献［7］给出了Carleman不等式的一种新改进，并建立如下不等式

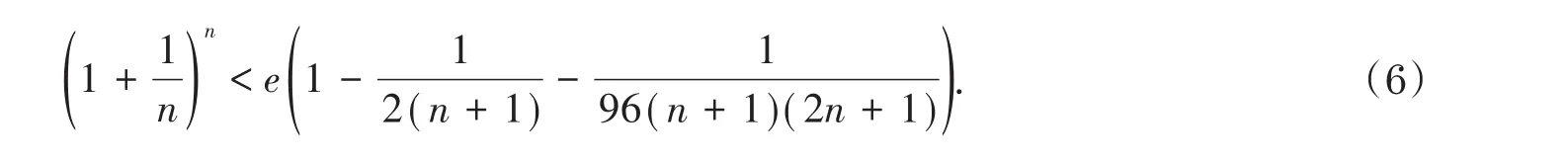
本文在式（5）（6）式的基础上，优化和改进了Carleman不等式，给出如下定理.

定理2当n≥7时，有

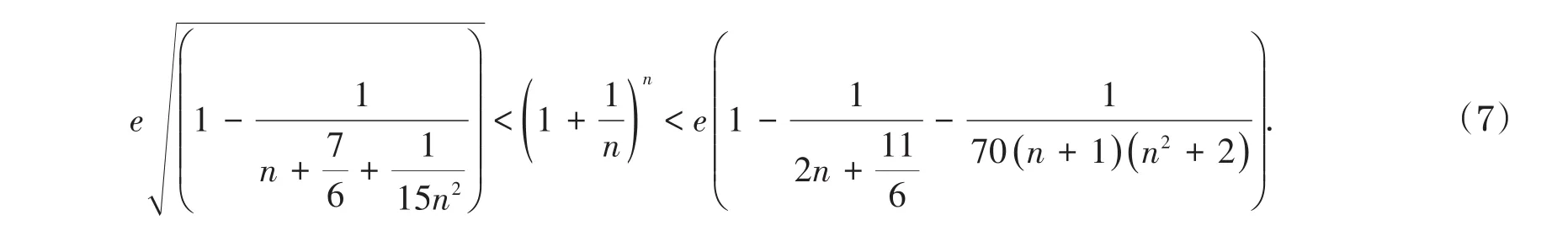
最后得出了如上的Carleman不等式的改进式。本改进式基本可以较为精确地估计出的数值。由于最新的改进式的收敛速度较为迅速，Carleman不等式的级数形式进行了高数量级的逼近优化。

1 定理2的证明

证明：令f(n)=nln，则当 n≥7时

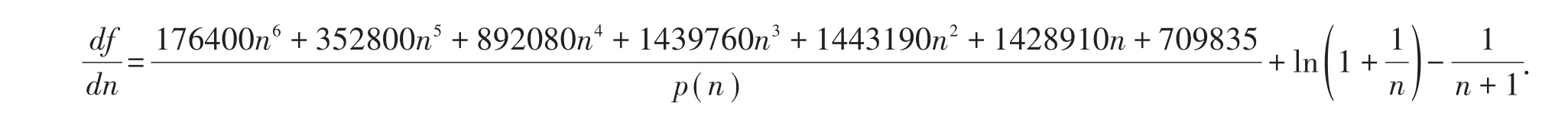
其中，p(n)=352800n8+1176000n7+2839550n6+5438860n5+7245070n4+7640045n3+6219605n2+2932650n+530530.

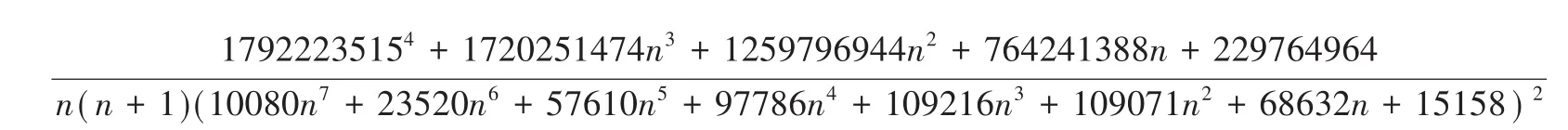
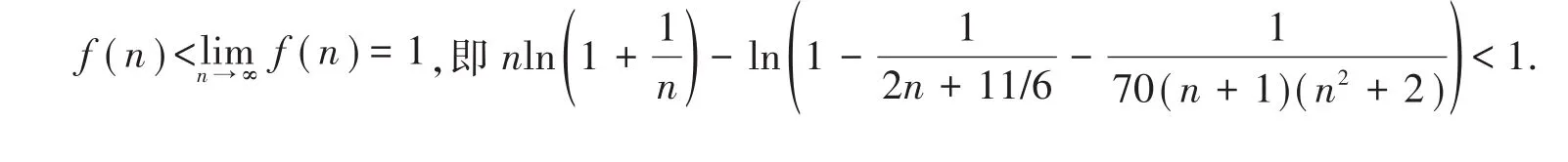
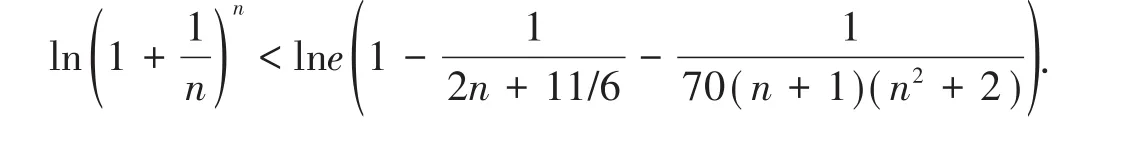
故

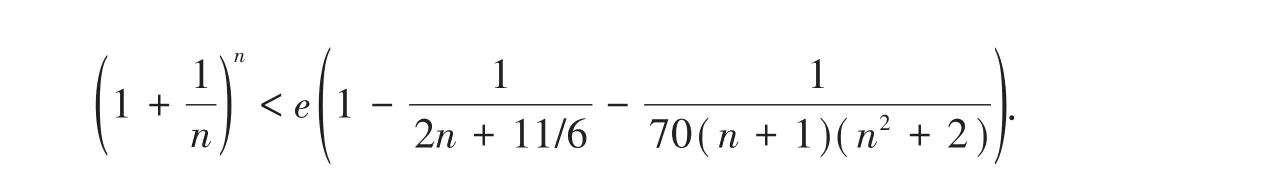
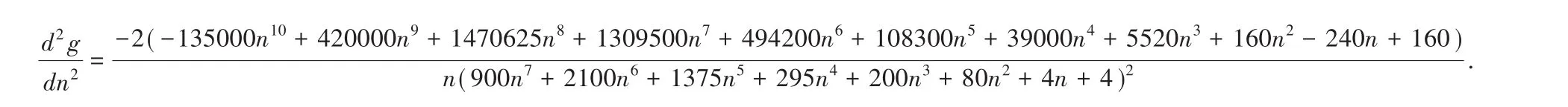
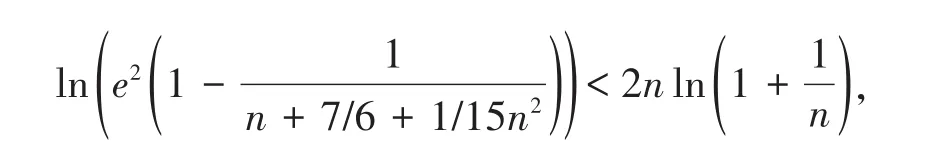
于是e2，故

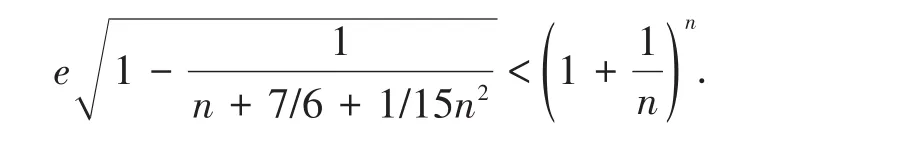
证毕.

2 几种Carleman双边不等式的对比分析

表1、表2为几种Carleman双边不等式对比分析。

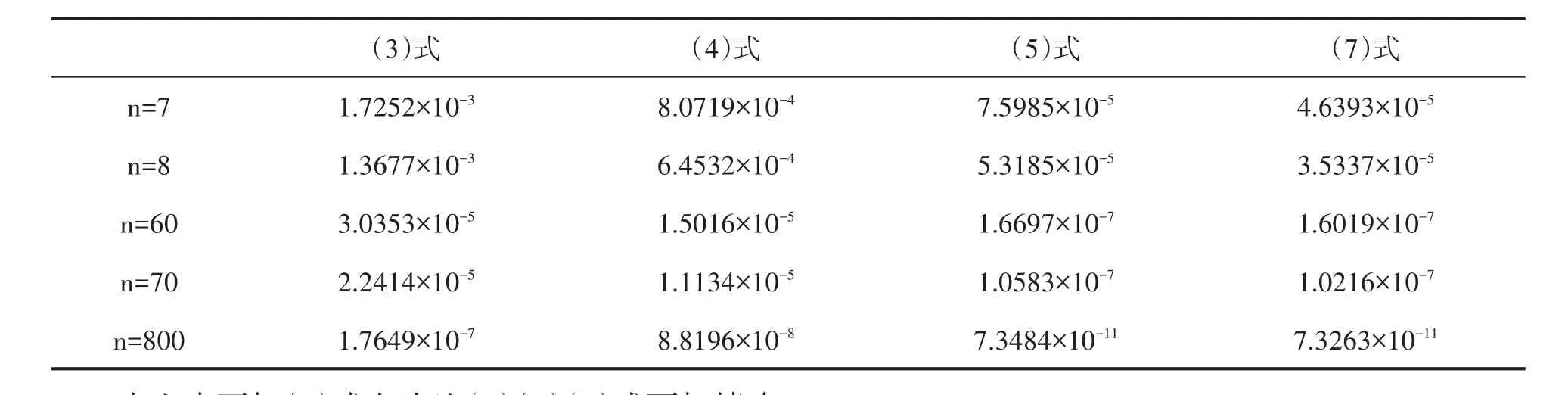
表1 各式左边项与中间项差的绝对值

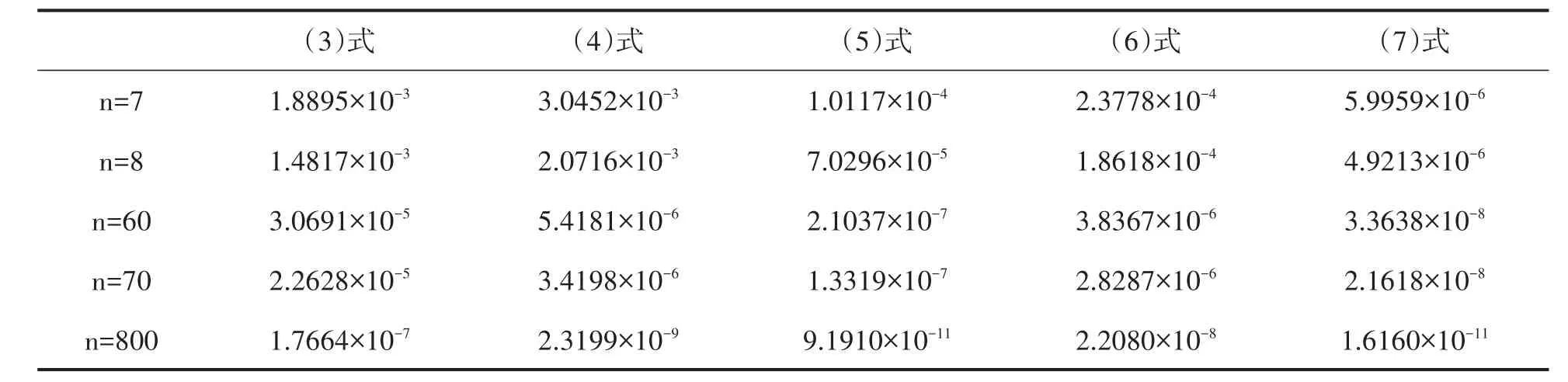
表2 各式左边项与中间项差的绝对值

由上表可知（7）式左边比（3）（4）（5）式更加精确 .

由上述表格可知，（7）式右边比（3）（4）（5）（6）式更加精确 .