蜗卷弹簧缺陷的周向导波检测

(广西电力有限责任公司 科学研究院，南宁 530012)

近年来，超声导波检测技术快速发展，特别是在板状和管状等波导结构中的应用日趋成熟[1-2]，相比传统的超声波检测法，超声导波对结构表面或内部的裂纹等缺陷进行大面积长距离的检测具有很大优势。

戴翔等[3]通过计算不同激励角度下的厚壁管道周向导波传播特性，优化了探头的入射角度，研究了周向导波与厚壁管道壁厚方向不同位置缺陷的相互作用，发现不同激励角度对壁厚方向不同位置缺陷的检测灵敏度不同，当入射角度为45°时，整个壁厚范围上的缺陷都能够被检测。HAYASHI等[4]开发了一种用于弯管结构的半解析有限元法，并通过数值模拟得到弯管结构导波的传播特性，计算了经过4个弯管区域后的导波回波信号，得到导波在弯管区域会发生模态转换的结论。张旭等[5]计算了铝环在2.5 MHz中心频率时最低阶模态的频散特性，并利用该模态对铝环进行检测，发现导波在铝^环内壁缺陷处会发生模态转换。吴斌等[6]通过对比不同入射角的斜探头组合，优化选取信噪比较好的斜探头在厚壁管道中激励出C-Lamb3模态导波对缺陷进行了检测，并证明了周向导波的指向性。YU等[7]基于线性三维弹性理论，采用正交多项式级数展开法确定均匀各向异性球形曲面板中的导波频散特性和位移分布，计算了不同曲率半径下正交各向异性球面曲线板的导波频散曲线，讨论了曲率半径对波传播特性的影响。王国峰等[8]提出基于椭圆法的圆管损伤定位，并通过在圆管上引入切槽损伤、孔损伤进行验证，对损伤大小、位置对定位误差的影响进行了分析。励争等[9]将连续小波变换应用到周向导波检测技术中，提出了一种以冲击载荷作为导波激励源，且适于薄壁管道内部径向裂纹检测的导波检测方法，该方法可定量地检测出圆环内部径向裂纹的位置，并进一步判断裂纹的损伤程度。

以上的研究都是以固定曲率的管状或者球状波导结构为研究对象，对于蜗卷弹簧等变曲率弯板结构的导波检测研究很少有报道。蜗卷弹簧各圈曲率变化不大，且轴向距离很短，因此对于此类构件的周向导波检测，不仅可以实现轴向和径向缺陷的检测，而且耗时少，只需移动传感器进行轴向扫查便可获取蜗卷弹簧整个厚度上的缺陷信息，实现对缺陷的快速检测和定位。因此，笔者把要检测的蜗卷弹簧外圈近似为固定曲率的空心圆柱体结构，通过数值求解该空心圆柱体的周向导波群速度频散曲线，来表征蜗卷弹簧外圈周向导波的传播特性，并由周向导波频率和入射角之间的关系选择探头的中心频率和入射角，搭建周向导波试验系统，对弹簧缺陷区域和非缺陷区域进行检测，通过端面回波分析计算导波群速度，验证是否激励了特定的周向导波模态，根据缺陷回波以及声程计算缺陷的位置，实现缺陷的定位。

1 蜗卷弹簧周向导波检测原理

以蜗卷弹簧实际使用中最易产生缺陷的最外圈为研究对象，研究周向导波在蜗卷弹簧最外圈的传播特性，建立与其曲率近似的内外表面均为自由表面的空心圆柱体结构，基本参数如表1所示。利用弹性力学知识以及边界条件推导,能得到该空心圆柱体周向导波频散方程，推导过程可参照文献[10-12]。通过对频散方程进行数值求解可得到蜗卷弹簧周向导波群速度频散曲线(见图1)。从图1可以看出，在频率为01.5 MHz范围内存在10个导波模态，且每个频率下至少存在两个导波模态，在不同频率下各模态频散程度不同。如何选取合适单一的导波模态对卷簧进行检测是一个关键的问题。由Snell定律，楔块材料纵波波速为2 337 m·s-1，可计算出周向导波频率和探头入射角以及导波模态的关系(见图2)。由图2可以看出,在特定频率和探头入射角度下，可以激励出单一的周向导波模态。由于低阶模态的导波在材料中的衰减小，且模态结构简单，导波检测中多采用低阶导波模态进行检测。由图2可知，选择的楔块角度过小会导致激发的模态较多，从而影响检测分辨率，因此应选择较大的角度入射才能激励出较为单一的导波模态。根据蜗卷弹簧导波检测的实际情况，采用中心频率为1 MHz的导波传感器以及52°楔块的组合探头在蜗卷弹簧中激励1模态的周向导波进行检测。

表1 空心圆柱体结构基本参数

图1 蜗卷弹簧周向导波群速度频散曲线

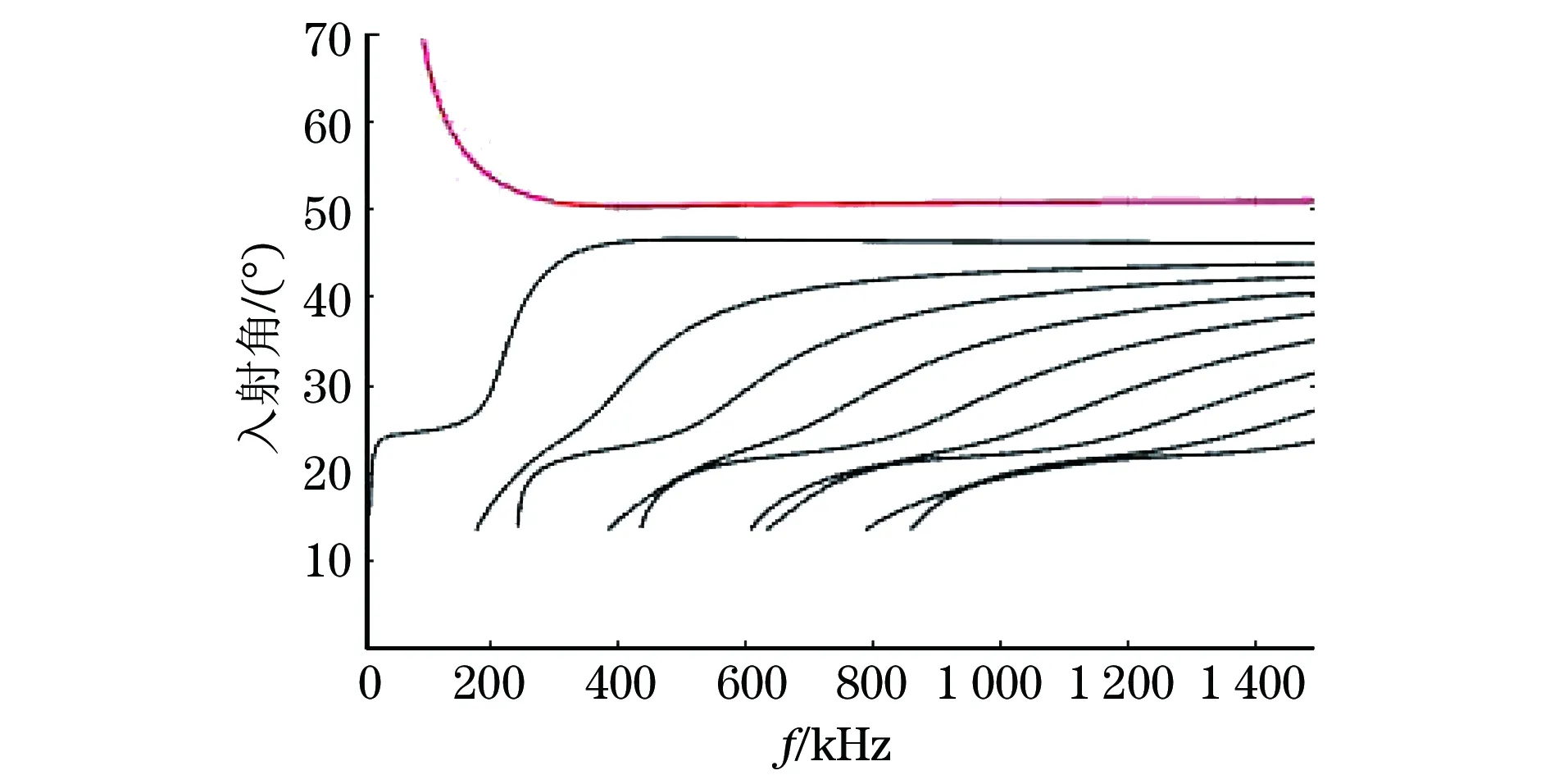
图2 导波频率和探头入射角的关系

图3 周向导波检测试验系统示意

2 蜗卷弹簧周向导波检测

试验装置主要由RAM-5000-SNAP系统、示波器、计算机、匹配电阻和1个导波探头等组成(见图3)。RAM-5000-SNAP系统作为信号发生和接收器，可通过计算机调节其激励信号宽度和增益，利用示波器观察发射和接收的时域波形。为了降低周向导波的频散，使得接收波形易于分析，激励信号应尽量选择窄带信号，试验采用10个周期的正弦信号作为激励信号，且利用一个导波探头自激励自接收的方式进行检测，目的是为了减小由于两个探头接收带来的系统误差，降低耦合程度不一或对探头施压不同等因素对回波幅值的影响。蜗卷弹簧外圈展开及传感器分布示意如图4所示，蜗卷弹簧外圈长为855 mm，宽为120 mm，厚为11.5 mm。在蜗卷弹簧外表面，距离周向右端面315 mm和515 mm处分别有两个轴向长为3 mm，宽为1 mm，深为0.5 mm的预置缺陷，两个缺陷距离蜗卷弹簧同一横截面的距离都为45 mm。采用选定的组合探头，通过改变探头前端与缺陷的距离,以及探头前端与端面的距离来对缺陷回波进行分析，探头尺寸(长×宽)为35 mm×25 mm。探头分3个区域进行检测，分别为无缺陷区域、1个缺陷区域和2个缺陷区域。在无缺陷区域,将探头布置在距离下截面25 mm，周向距离分别在400 mm以及700 mm处;在1个缺陷区域，将探头布置在距离上截面30 mm，周向距离分别在400 mm和500 mm处;在2个缺陷区域，将探头布置在距离上截面30 mm，周向距离在200 mm和300 mm处。

图4 蜗卷弹簧外圈展开及传感器分布示意

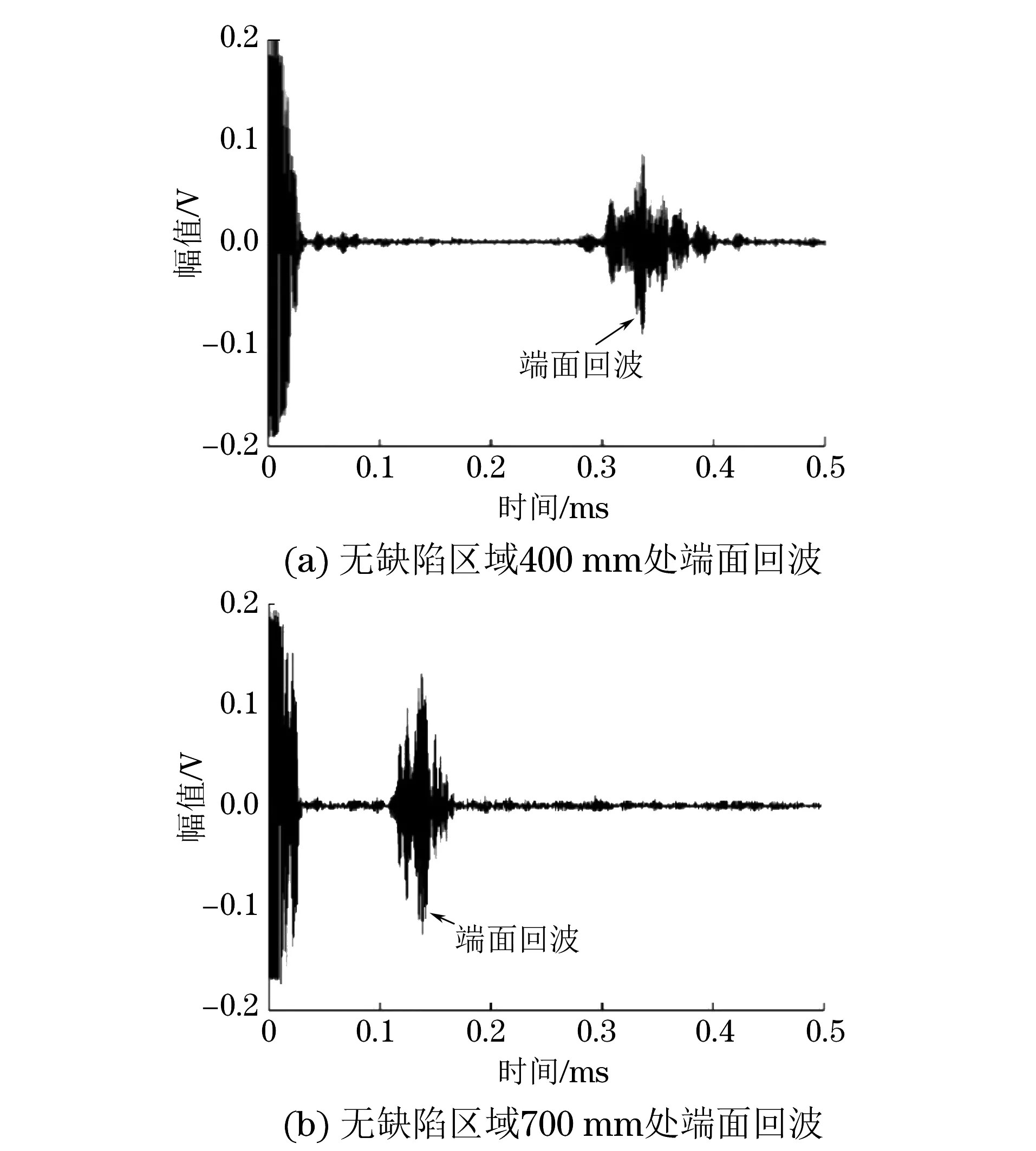
图5 无缺陷区域的检测结果

对无缺陷区域的端面回波进行研究，探头前端距离端面分别为455 mm和155 mm时接收到的回波波形分别如图5所示。图5(a)中端面回波时间为0.336 2 ms，图5(b)中端面回波时间为0.134 4 ms，两种情况下探头和端面的距离差为300 mm，由此可以计算激励的周向导波群速度为2 973 m·s-1，与第1导波模态理论值2 998 m·s-1的相对误差为1%，说明通过选定的频率和入射角可激励出需要的1模态导波，且该模态经过端面反射后回波模态不变。由上述数据还可以计算出导波在探头中的传播时间为0.015 ms。

对有1个缺陷的区域进行回波分析，探头前端距离缺陷分别为140 mm和40 mm，距离端面分别为455 mm和355 mm，接收到的波形分别如图6所示。图6(a)中缺陷回波时间为0.12 ms，端面回波时间为0.337 ms；图6(b)中缺陷回波时间为0.052 6 ms，端面回波时间为0.27 ms，再由两种情况下,探头前端和缺陷的距离差为100 mm，可计算出缺陷回波群速度为2 967 m·s-1，探头和端面距离差为100 mm，可计算出端面回波群速度为2 985 m·s-1，与理论值相符。说明在经过缺陷和端面反射后，导波模态没有发生模态转换，可通过该模态群速度、回波时间以及探头传播时间计算缺陷距楔块前端的距离，实现缺陷的定位。

图6 1个缺陷区域的检测结果

图7 2个缺陷区域的检测结果

对有两个缺陷区域的回波进行分析，探头前端距离第一个缺陷分别为140 mm和40 mm，距离第二个缺陷分别为340 mm和240 mm，距离端面分别为655 mm和555 mm，接收到的波形如图7所示。图7(a)中第一个缺陷回波时间为0.116 7 ms，第二个缺陷回波时间为0.05 ms，端面回波时间为0.463 2 ms；图7(b)中第一个缺陷回波时间为0.05 ms，第二个缺陷回波时间为0.186 7 ms，端面回波时间为0.396 ms，由两种情况下探头和第一、第二个缺陷距离差,以及和端面距离差均为100 mm，可计算出第一个缺陷回波群速度为2 998 m·s-1，第二个缺陷回波群速度为2 981 m·s-1，端面回波群速度为2 976 m·s-1，与理论值2 998 m·s-1都很接近，说明周向导波在经过第一和第二个缺陷以及端面后都未发生模态转换，再次说明了利用激励模态的群速度计算缺陷位置的可行性。对比图5(a)，6(a)，7(a)还可以发现，距离端面越远，导波回波幅值越小，能量衰减越大。当探头和端面间无缺陷时，无法检测到缺陷回波，在探头覆盖缺陷时，缺陷回波很明显，说明周向导波有很强的指向性，因此应按照严格的轴向步长进行周向导波检测，避免发生漏检。

3 结语

通过数值求解了蜗卷弹簧外圈群速度频散曲线，选择能激励特定导波模态的探头，利用周向导波对蜗卷弹簧外圈进行了缺陷检测。通过对回波的计算分析，验证了1 MHz频率的传感器以及52°楔块的组合探头能够激励出1模态的周向导波。并且在检测区域含有多个缺陷的情况下，缺陷回波都不会发生模态转换，由此可通过激励模态的群速度、回波时间以及探头传播时间计算缺陷距楔块前端的距离，实现缺陷的定位。最后验证了周向导波的指向性，为工程实际检测做指导。

致谢计算分析得到了广西大学机械学院的覃小倩、黄应翔和唐伟力等的热情帮助，在此表示由衷感谢。