回归正交设计在车速再现不确定度评定中的应用

中汽研汽车检验中心(武汉)有限公司 杨文飞 李勰 王旭敏

道路交通事故司法鉴定实践中的车速再现一般通过特定的模型进行计算，利用回归正交设计方法对典型的车-人碰撞事故的车速再现模型进行不确定度分析，通过正交试验设计、回归分析以及参数取值范围得到车速的不确定度，通过与不确定度评定基本方法的结果进行对比，两者十分接近。通过极差分析表明车-人事故中人体与路面的摩擦系数μ对车速再现结果影响最大，这对实际司法鉴定中车速再现不确定参数的勘测和选取具有指导意义。最后通过一起典型车-人事故的车速再现，验证了上述方法在司法鉴定实践中应用的可行性和准确性。

近年来，随着整个社会的法制、维权意识的增强和提高，对道路交通事故责任认定起重要作用的车辆行驶速度再现越来越受到事故各相关方的重视和关注。目前，道路交通事故中事故车辆行驶速度的再现方法主要包括基于事故形态、基于软件模拟、基于车载记录数据和基于视频图像等4种车速再现方法[1]，其中基于事故形态和视频图像的速度再现方法在司法鉴定实践中应用广泛，且都形成了国家标准[2,3]。根据具体事故中能够提供的鉴案材料或勘验资料，鉴定人员选择合适的方法进行车速再现分析，有时也在同一个事故中利用多种方法计算的结果进行相互验证。国家标准[2]给出了各种模型的计算公式和不同类别摩擦系数取值范围，在实际事故勘查中获取的制动印痕长度、变形量、抛距等参数大多时候是一个取值范围。因此，通过所收集的参数计算得出车速再现的不确定度就能够增加车速再现结果的科学性和可信度，并且在一定程度上可以排除主观因素对结果的影响。许多学者已对不确定度基本评定方法[4]、蒙特卡洛评定方法[5-7]、上下界评定法、差分评定法以及响应表面评定法[8]做过研究，但多是针对给定软件模拟初始值而进行研究。本文针对事故车速再现司法鉴定的具体实践，把回归正交设计方法应用于典型车-人事故车速再现结果的不确定度分析与计算中，所得车速再现结果与不确定度基本评定方法所得到的结果十分接近，从而论证了回归正交设计方法的科学性和有效性。通过一个实际车-人碰撞事故案例，对回归正交设计方法应用于车速再现司法鉴定实践的可行性进行了验证和说明。

回归正交设计方法

为了利用正交试验设计和回归分析两种方法的优势，统计学者提出了回归正交设计方法，通过这种方法不但能构建合理的试验设计，而且只需较少的试验次数就能得到有效的数学模型[9]。回归正交设计可以在因素的试验范围（或称取值区间）内选择适当的试验点，用较少的试验建立一个拟合精度高、统计性质好的一次回归方程，进而解决不确定度评定的问题。在车速不确定度评定的应用中，应用此方法可以计算得到非线性车速再现模型的一次回归方程，从而解决非线性车速再现模型的不确定度评定分析问题。

1．试验设计

被广泛应用于各行各业的正交试验设计的“整齐可比、均衡分散”的特点是通过正交表进行试验设计来实现的[7]。回归正交设计表可以通过正交表变换得到，即将二水平正交表中的“2”用“-1”代换。正交表L（27）经过变换后8得到的回归正交设计表，其中的“1”表示因素的上水平，“-1”表示因素的下水平。回归正交设计表中任一列编码的和为零，任两列编码的乘积之和等于零，这表明通过正交表得到的回归正交设计表同样具有正交性。

2.试验方案的确定

根据正交表L（27）的表头设计表，可以进行相应

8的回归正交设计表的表头设计。在考察三个因素的情况下，各因素应分别放在第1、2和4列[9]，用相应参数的上、下水平值依次替换回归正交设计表中的“1”和“-1”就可以得到最终的试验方案。

3.回归分析原理和步骤

回归正交设计的总思想就是利用正交设计、回归分析原理，建立试验指标(y)与m个试验因素x1，x2…，xm之间的回归方程：

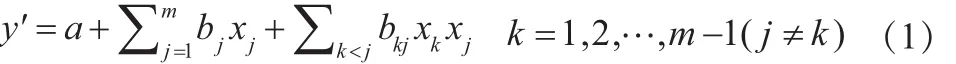
若不考虑因素间的交互作用，即式(1)中的交互项，则回归方程为一次多元线性方程：

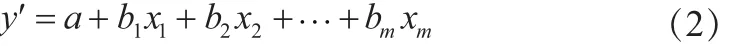
式中，x为各因素的输入量，x=(x1，x2，…，xm)T；y′为试验指标的输出量；m为输入变量个数；a,b,b1,b2,…，bm为回归系数。

基于事故形态的车速重建再现本质上可以看作是一个由物理方程组组成的再现模型，其中用于计算车速的不确定参数是再现模型的输入量，计算得到的车速是再现模型的输出量。试验方案确定后，就可以根据车速再现模型得到试验结果，再通过回归分析确定式(2)中的回归系数，从而得到车速再现模型的一次回归方程，最后利用不确定参数的取值范围通过上下界法来确定车速再现结果的不确定度。

典型车-人碰撞事故车速再现不确定度分析

以文献[4]中的典型车-人碰撞事故中车辆行驶速度再现模型为例，说明和验证回归正交设计方法应用于车速再现不确定度分析中的可行性和科学性。该车速再现模型是非线性的，计算公式为：

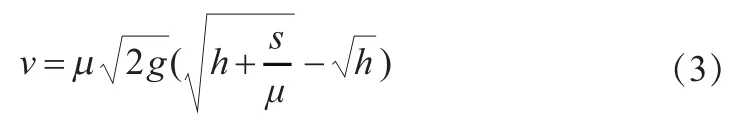
式中，h为人体的抛出高度；μ为人体与路面的摩擦系数；s为人体的抛出距离；g为重力加速度。参数h、μ和s在实际事故中的勘验和选取过程中都会产生不确定性，因此确定这3个参数为此计算模型的不确定因素。根据文献给出的数据，这三个不确定因素取值范围分别为h=0.93±0.1m，μ=0.6±0.1和s=18.8±0.5m。根据前文的试验方案设计进行试验，得到的试验结果如表1所示。

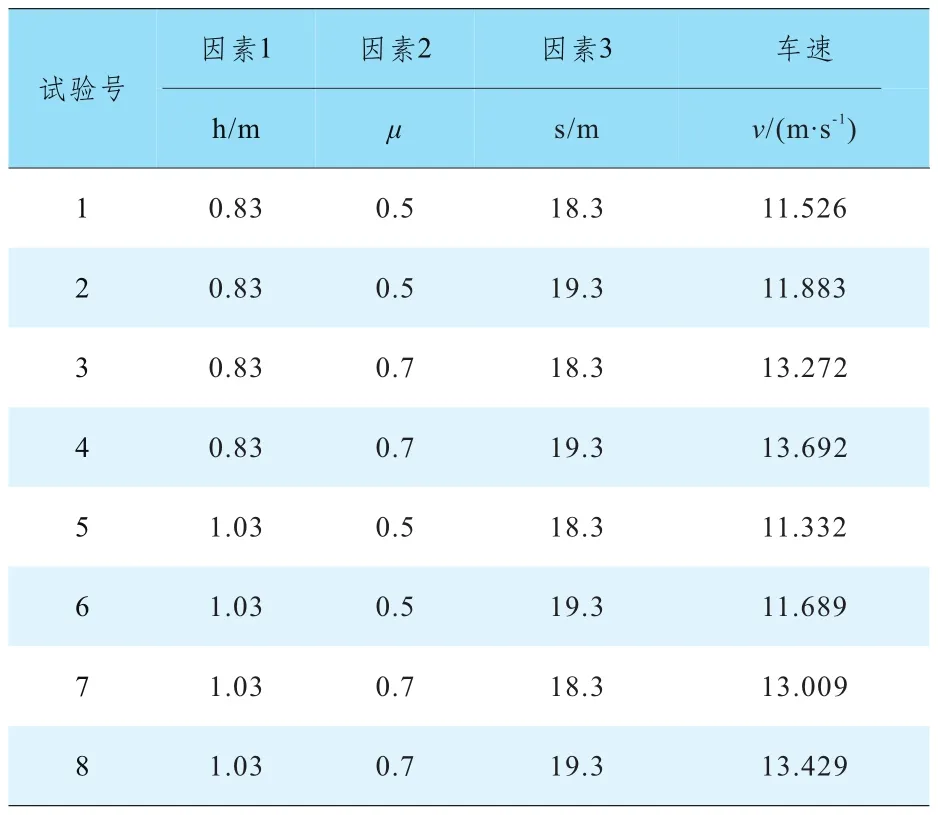
表1 回归正交设计试验方案和试验结果

通过回归分析，计算得到车速再现模型(3)的一次回归方程为：

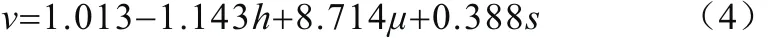
回归分析的检验结果如表2所示。回归方程(4)总体拟合优度（调整后的R2）为0.999，且通过了方差F检验，表明此回归方程总体显著；从回归系数的检验来看，三个自变量因素回归系数的p值均小于0.05，因此，三个自变量因素均对车速v有显著影响，所以回归方程(4)可以高度拟合典型车-人碰撞事故的车速再现模型(3)。

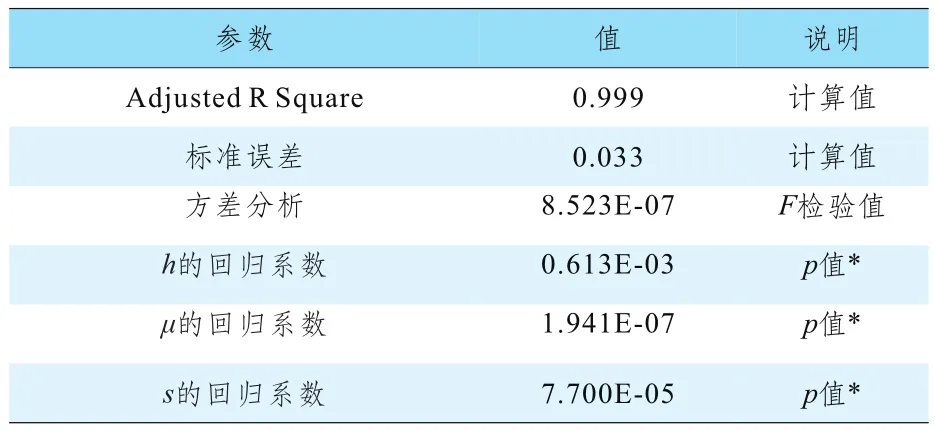
表2 回归方(4)的统计检验

根据式(4)和不确定因素的取值范围利用上下界法就可以计算得到车速再现结果的不确定度。为了验证回归正交设计方法的科学性和有效性，与文献[4]中的不确定度评定基本方法计算所得结果进行比较，两种方法的结果对比如表3所示。

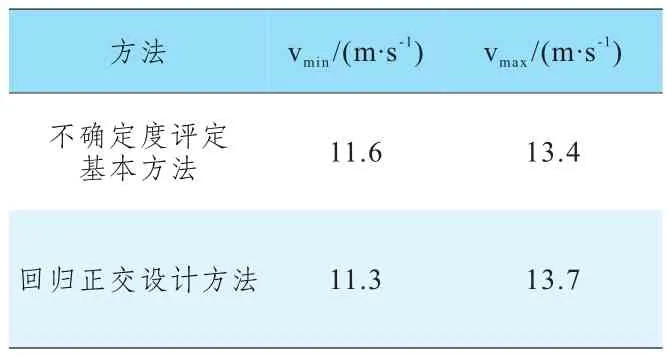
表3 不同方法不确定度评定结果的对比

从表3可以看出，两种方法所得结果十分接近，各自上、下界值的偏差都在3%以内，从而有效地说明和验证了回归正交设计方法的科学性和有效性。

不确定因素对车速再现的影响

极差法能够直观、有效地处理和分析正交试验的结果数据[10]。由上文可知，通过正交表得到的回归正交设计表同样具有正交性，因此能够利用极差法对回归正交设计试验结果进行对比分析。由表1试验结果计算得到各因素不同水平的极差如表4所示。表中Ij表示各因素4次下水平试验值的加权和，IIj表示各因素4次上水平试验值的加权和，Rj表示各因素不同水平加权和的极差。

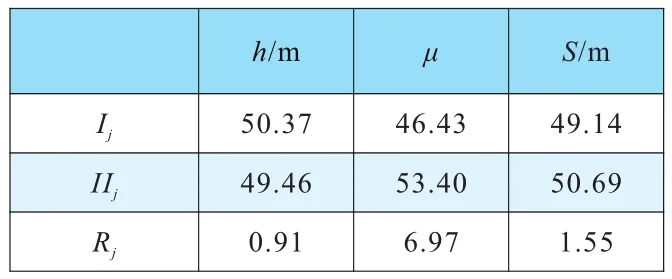
表4 不确定因素的极差

由表4可知Ru>RS>Rh，即在典型车-人事故车速再现中，不确定因素对车速再现结果的影响由强到弱的顺序为：人体与路面的摩擦系数μ、人体的抛出距离s、人体的抛出高度h。通过极差比较可知，人体与路面的摩擦系数μ对再现结果的影响远大于人体的抛出距离s和人体的抛出高度h，因此在车-人碰撞事故车速再现的司法鉴定实践中，应该更加注重人体与路面的摩擦系数μ的选取，进而提高车速再现结果的科学性与准确性，这对车速再现司法鉴定工作中不确定参数的勘验和选取具有一定指导意义。

实际车-人碰撞事故车速再现

为了验证回归正交设计方法应用于车速再现司法鉴定实践的可行性，选取一个实际的车-人碰撞事故说明上述方法在司法鉴定实践中的应用。某日下午19时许，在某市一条主干道上，一位过马路的行人被一辆水泥搅拌车撞倒。根据交警调查和事故现场图得到行人抛距取值区间为[17.8，18.3]m；抛出高度取值区间为[0.95，1.05]m；人体与地面的摩擦因素取值区间为[0.55，0.65]。

利用前文所述方法计算得到得到式(3)的回归方程为：

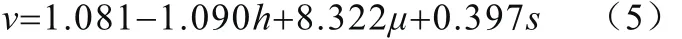
回归方程(5)的总体拟合优度（调整后的R2）为0.999，且通过了方差F检验，因此回归方程总体显著，再利用不确定因素的取值区间通过上下界法计算得到此次车-人碰撞事故车速再现结果为[42，46]km/h。

另外根据行车记录仪的视频记录计算的车速约为45 km/h，即通过回归正交设计方法得到的车速不确定度涵盖了45 km/h这一速度值。在视频图像足够清晰，参考物容易确定的情况下，通过视频图像计算的车速是比较准确的[3]。因此，利用回归正交设计方法计算的速度不确定度区间包含了相对准确的速度值45 km/h，说明此方法能够应用于车速再现的有关司法鉴定实践,特别是在许多案件由于现场条件缺乏视频图像等鉴案资料的情况下，更能显示出此方法的优越性。

结语

本文采用回归正交设计方法对典型的车-人碰撞事故车速再现结果的不确定度进行了研究，首先通过正交试验设计和回归分析得到典型的车-人碰撞事故车速再现模型的回归方程，再结合不确定性因素的取值区间和上下界法计算得出了车速的不确定度区间，所得结果与不确定度基本评定方法所得结果十分接近，验证了回归正交设计方法的科学性和有效性。接着通过极差分析得到，相比于人体的抛出距离s和人体的抛出高度h，人体与路面的摩擦系数μ对车-人碰撞事故车速再现结果影响更大，这对司法鉴定实践中的车速再现分析具有一定的指导意义。最后，通过一起真实道路的车-人碰撞事故验证了回归正交设计方法应用于车速再现司法鉴定实践的可行性和准确性。