利用旋转法妙解一类解三角形问题*

●邓 城

(增城中学,广东 广州 511300)

高中数学中的解三角形问题一般利用正弦定理和余弦定理等方法来解决，其解题特点是充分利用已知条件建立等式，同时注重对各种量的处理，往往需要一定的变形化简技巧，计算量有时较大.然而对于某些具有特殊几何条件的解三角形问题，采用几何中旋转图形的方法比用正余弦定理的方法更加简捷直观.现举例展示如下：

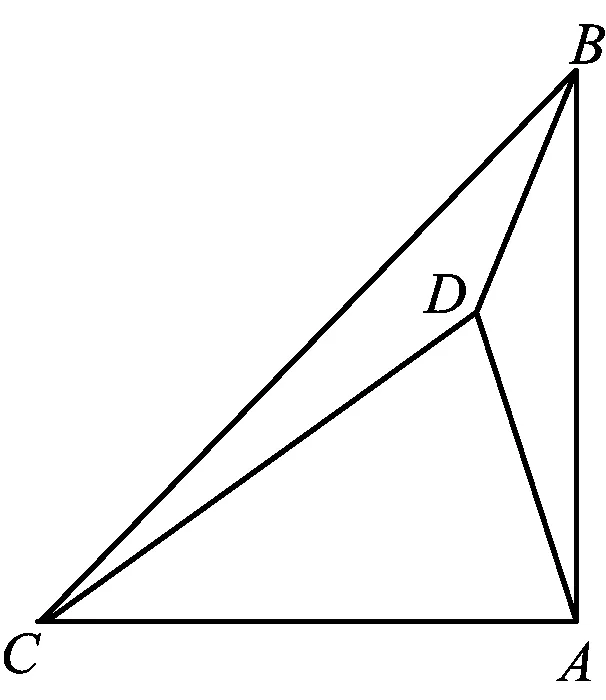
图1

例1 如图1所示，点D是△ABC内部的一点，AB=AC，∠BAC=90°，DB=3，CD=5，∠BDA=135°，求AD的长.

分析 题目从表面看属于常规的解三角形问题，已知条件有边有角，容易想到从正余弦定理的角度寻找关系式，通过一个或几个方程来求出AD的长.

由于题目中条件DB=3,CD=5和∠BDA=135°并不是在同一个三角形中，这使得要使用正余弦定理的话还需再引入几个量，并且要考虑好正余弦定理用在何处.

解法1 设AD=x，AB=y，∠BAD=θ,在△ABD中，由正弦定理得

(1)

由余弦定理得

y2=BD2+x2-2x·BD·cos 135°=

(2)

在△ADC中，由余弦定理得

CD2=CA2+AD2-2CA·AD·cos(90°-θ),

化简得

25=x2+y2-2xy·sinθ,

(3)

将式(1)、式(2)代入式(3)，得

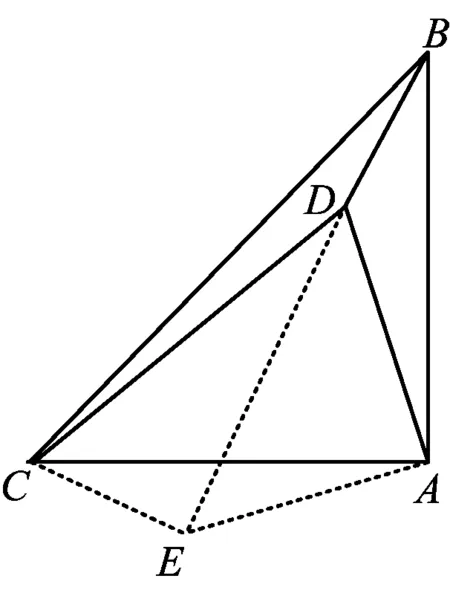
图2

点评 以上解法需要想到添设∠BAD=θ和AB=y，并用了一次正弦定理和两次余弦定理，有一定的思考难度和变形化简难度，综合性较强.但若注意到△ABC是等腰直角三角形，且∠BDA=135°是个特殊角，可以尝试考虑旋转三角形，将某些边旋转到不同位置，构建新的几何关系.

解法2 由于AB=AC，∠BAC=90°，将△ABD绕点A逆时针旋转90°得到△ACE，如图2所示.由旋转性质易得△ADE是等腰直角三角形，∠CEA=135°，从而

∠CED=135°-45°=90°，

于是

CD2=CE2+DE2.

又由旋转性质知CE=BD，得

CD2=BD2+DE2，

因为△ADE是等腰直角三角形，所以

DE2=2AD2，

故

CD2=BD2+2AD2，

点评 从上面解题过程可以发现：旋转法非常巧妙，稍微旋转一下居然就能扭转乾坤，但细心之下不难发现旋转法的巧妙还是需要题目条件的“精心”配合.假如AB≠AC，旋转起不到什么作用；假如∠BDA≠135°，则△CDE也不是直角三角形.另外，使用旋转解法一定是要旋转△ABD吗？注意到AB可以逆时针旋转90°到AC，也可以由AC顺时针旋转90°到AB，因此也可以考虑旋转△ACD.

图3

解法3 将△ACD绕点A顺时针旋转90°得到△ABE，如图3所示.然后证明△BDE是直角三角形，方法与解法2类似，在此不再赘述.

变式1 如图4，点D是△ABC外部的一点，AB=AC，∠BAC=90°，∠BDA=45°，DB=3，CD=5，求AD的长.

图4 图5

分析 与例1对比，点D在△ABC外，但∠BDA=45°，是个特殊角，仍然可以尝试考虑旋转法.类似例1的解法3，可将△ACD绕点A顺时针旋转90°得到△ABE，如图5所示.然后证明△BDE是直角三角形，过程与例1几乎一样.

变式2 如图6所示，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC.试确定AD,BD,CD三者之间的数量关系.

图6 图7

分析 注意到题目中的条件AB=BC以及∠D和∠B均为特殊角，可尝试旋转法.可将△ABD绕点A逆时针旋转60°得到△ACE，如图7所示.易得

CE=BD，AE=AD， ∠EAD=60°，

从而△EAD是等边三角形，于是

ED=AD， ∠EDA=60°.

因为∠ADC=30°，所以

∠EDC=∠EDA+∠ADC=90°，

故

CE2=ED2+CD2，

即

BD2=AD2+CD2.

由于△ABC是等边三角形，因此采用旋转法时还可以旋转△BCD，将△BCD绕点B逆时针旋转60°，后续解法大同小异.

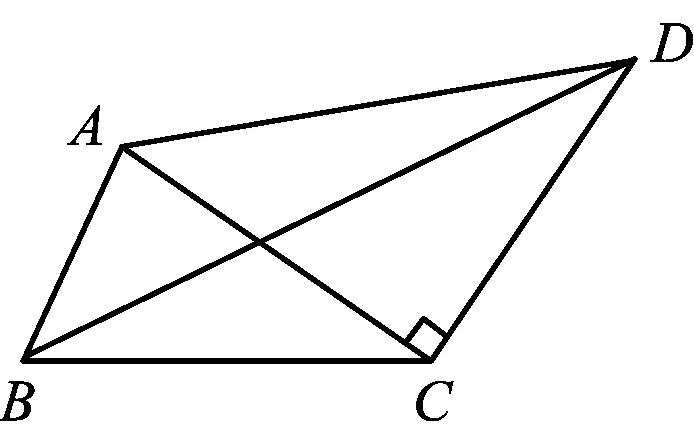
图8

分析 注意到题目条件中出现了边长和垂直的条件，问的又是∠ABC变化时的情况，容易想到可从解三角形的思路入手，通过正余弦定理来解决.

AC2=AB2+BC2-2AB·BC·cos∠ABC，

即

由正弦定理知

得

在△BCD中，

BD2=BC2+CD2-2BC·CD·cos∠BCD=

由上可见，对于一道填空题来说，解法1非常复杂，计算量也很大，因此,我们应思考有没有更加简洁的解法.注意到AC=CD和AC⊥CD，可尝试通过旋转对角线BD所在的一个三角形来处理.

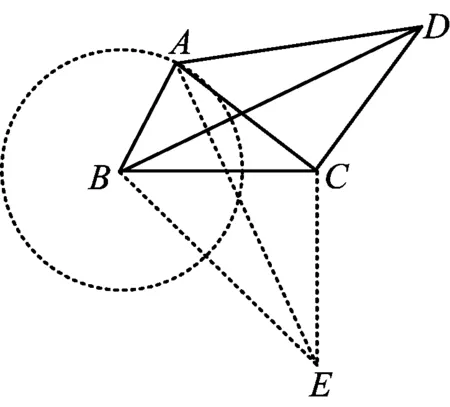
图9

点评 在原来的题目背景中，点D的运动轨迹难以判断，因此BD长度的最值问题通过三角解法直接处理比较麻烦.但是通过旋转，将BD的长度等价转化为EA的长度，点E是固定点，而点A又在圆上运动，此时EA的长度变化直观明了.

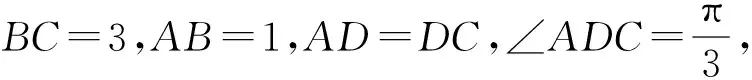
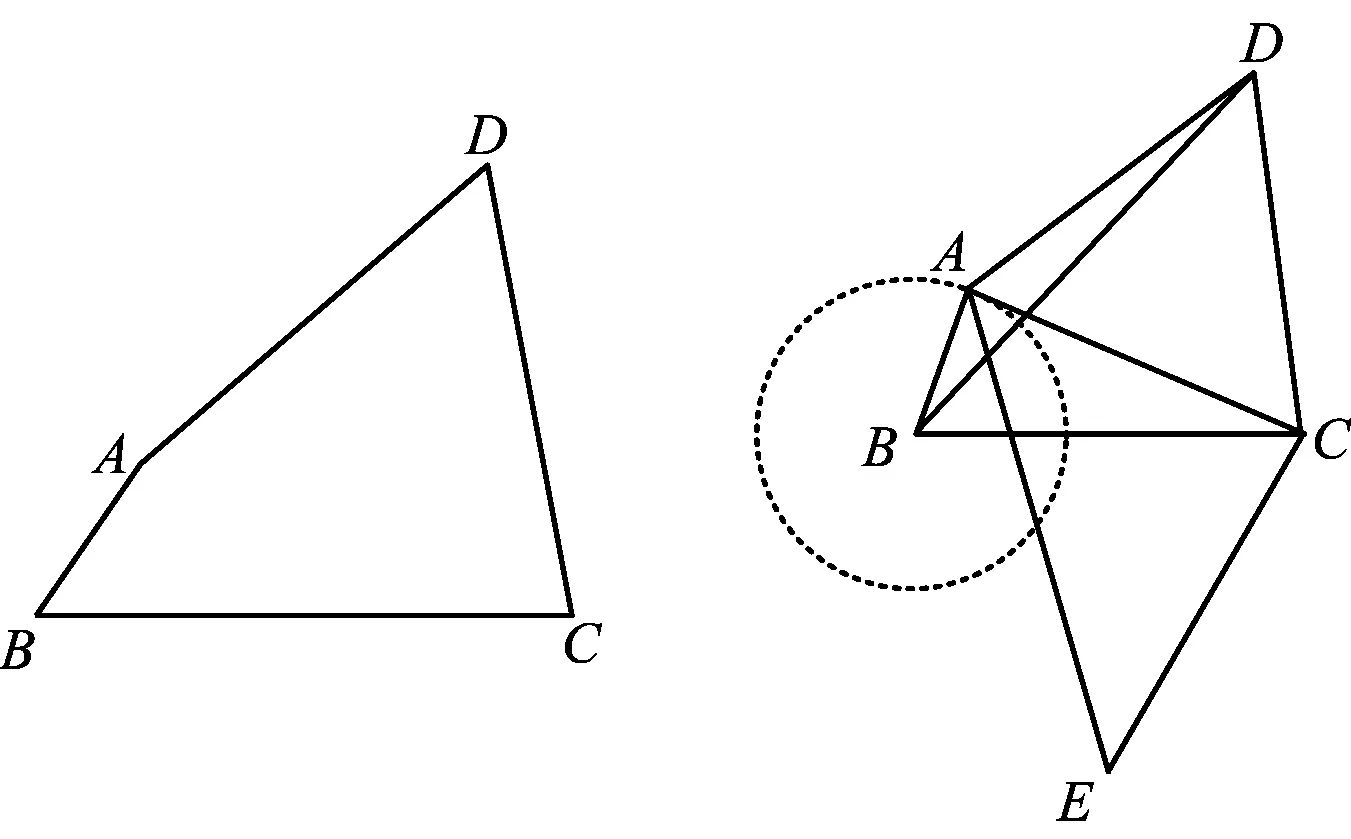
图10 图11

分析 将△BCD绕点C逆时针旋转60°得到△ECA，如图11所示.类似例2的解法，容易得到BD=EA≤EB+BA=3+1=4.

从例1、例2以及它们的变式题可以发现：当看似解三角形的题目有边长相等和出现特殊角的条件，并且用常规的三角解法比较麻烦时，不妨考虑旋转三角形，通过转换目标构建新的几何关系，巧妙解决问题.具体来说使用旋转法的操作方法分为3步：第1步是选取拟旋转的三角形.这个三角形的其中一边必须是等腰三角形中的一条腰，第二条边是所求的目标线段，第三条边一般是已知长度条件的线段.例如在例1中考虑旋转△ABD的原因是AB是等腰△ABC的一条腰，AD是所求边长，BD是已知长度为3的线段.第二步是将选定的三角形绕一顶点旋转题目中出现的特殊角度数(一般是题目条件中等腰三角形的顶角度数)，使得旋转后的一边与原来的一条腰重合.如例1中将△ABD绕点A逆时针旋转90°后，AB旋转到AC的位置.第三步是寻找旋转三角形后出现的新的几何关系并用来解决题目的所求问题，如在例1中旋转△ABD后利用旋转的性质结合已知条件发现△ABD是直角三角形，从而通过勾股定理解决问题.当然，从教学的角度来说，要先让学生熟练掌握解三角形问题的常规方法，在这个基础上，碰到符合上述特殊条件的解三角形问题时，可以进行一题多解的探究，让学生在对比之中感悟不同方法的本质和适用条件，培养学生分析问题和灵活应用方法的能力[1].