基于状态观测的双臂空间机器人分散容错控制

雷荣华，陈 力

（福州大学 机械工程及自动化学院，福州 350116）

空间机器人是由航天器与机械臂组成的一类复杂多体系统，它可以协助宇航员执行高风险的出舱任务，在空间探索领域发挥着巨大作用[1-5]。空间机器人的执行器频繁运行控制指令，极易发生部分失效故障，并对系统的姿轨控制性能造成极大影响。目前，关于空间机器人的容错研究鲜见报道，而对于其他非线性系统的容错控制研究也有待完善。

对于存在执行器故障与输出力矩受限的航天器，文献[6]提出了一种基于速度估计的容错控制器，该算法在确知执行器有效因子最小值的条件下实现了高精度的姿态容错控制。然而，对于实际的航天器，有效因子的最小值通常难以获取，从而阻碍了该控制策略的工程应用。针对存在执行器故障与参数不确定的航天器，文献[7]设计的一种自适应滑模控制器可以对有效因子的下界进行自适应估计和补偿，并实现了有限时间姿态跟踪控制，但该算法需要实时获取系统的角速度信号。文献[8]提出了一种基于故障在线估计的自适应容错控制算法，该算法具有无需获取任何故障信息的优点，但文中使用了六组神经网络函数，导致计算量庞大。

值得一提的是，与单臂空间机器人相比，双臂空间机器人具备更高的定位精度和承载能力[9-10]，因此具有更广阔的工程应用前景。但要实现双臂与载体的协调运动会加大建模与控制算法设计的难度。

考虑到当前研究现状，本文针对关节执行器存在部分失效故障的双臂空间机器人的控制问题，提出了一种基于状态观测器的分散神经网络容错算法。根据分散原理直接将执行器部分失效故障问题转化为参数不确定非线性系统的自适应容错控制问题。结合状态观测器得到了关节的角速度信号，从而无需实时测量和反馈关节的角速度信号；利用分散神经网络对系统的不确定项与交联项进行估计，从而无需确知任何故障信息。最后通过数值仿真示例校验了算法的有效性。

1 动力学建模

1.1 系统动力学模型

具有2n个关节的双臂空间机器人系统的平面结构如图1所示。该系统由载体（航天器）基座B0以及刚性臂杆Bi(i= 1 ,2,… ,2n)组成。载体B0可做平面转动与移动，臂杆Bi只能做平面转动。

图1 漂浮基双臂空间机器人系统Fig.1 Free-floating dual-arm space robot system

图1中：XOY为系统的惯性坐标系，xi oi yi为各分体Bi(i= 0 ,1,…,2n)的局部坐标系；分体Bi(i= 0,1,…,2n)的质量和中心转动惯量分别为mi和Ji；旋转中心O0与O1的距离为l0，机械臂Bi(i= 1 ,2,… ,2n)沿yi轴的长度为li；θ0为载体姿态相对Y轴的转角，θi(i= 1 ,2,…,2n)为相邻两连杆的相对转角；ω0=为载体的姿态角速度，ωi=θ˙i(i= 1 ,2,…,2n)为机械臂Bi的转动角速度。

对于自由漂浮的欠驱动（载体姿态不控）双臂空间机器人，利用第二类拉格朗日法可推导出系统的动力学微分方程为

为了获取系统完全能控形式的动力学模型，以便于后续控制策略的实施，可将式(1)表示为如下分块矩阵的形式：

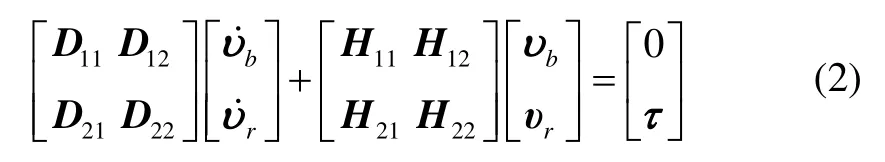
式(2)可进一步分解为

由于D(q)是正定的分块矩阵，故子矩阵D11的逆矩阵存在，并将其左乘式(3)，即可求得载体姿态角加速度将代入式(4)并整理可得如下完全能控形式的动力学方程：

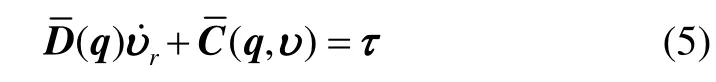
1.2 子系统的动力学模型

将双臂空间机器人系统的臂杆关节考虑为一个子系统，并从系统动力学方程(5)中分离出局部变量，可以得到子系统的动力学微分方程为[8]：

对于关节执行器存在部分失效故障的空间机器人，其执行器的理想输出与实际输出之间存在比例性偏差（有效因子）。此时，子系统的动力学模型为

其中：ρi∈(0,1]为表征执行器故障程度的有效因子，其值越小表示执行器故障程度越高；ρi=1与ρi∈(0,1)分别表示执行器正常运行和发生部分失效故障。

2 状态观测器设计

为了便于状态观测器的设计，不妨定义第i个子系统(i= 1 ,2,…,2n)的状态变量为则式(8)可以表示为如下的状态空间方程：

其中：

其中：Wif和Wig为理想神经网络的权值，和Φig(qri)为神经网络基函数，εif和εig为逼近误差，εi1与εi2为正常数。

定义神经网络的最小逼近误差为

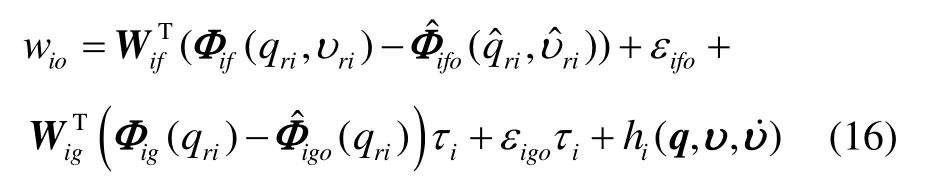
假设1 神经网络的最小逼近误差wio有界且满足

其中，ξio为正常数。

其中，k1i与k2i为正常数。

结合式(9)与(18)可得状态识别误差方程为

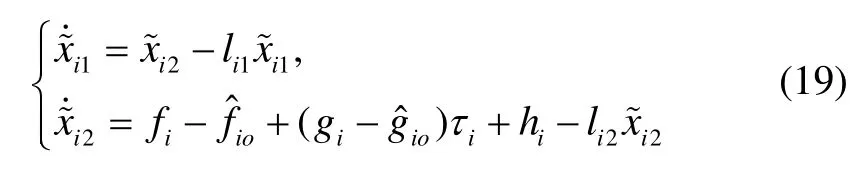
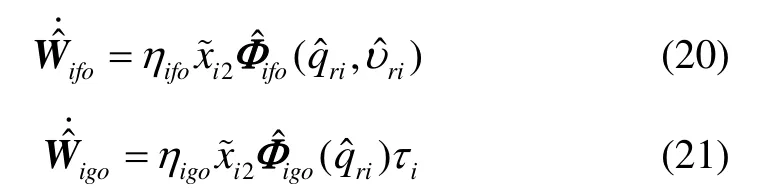
定理1对于状态未知的故障子系统(8)，在假设1成立的前提下，设计自适应更新律(20)与(21)，则分散状态观测器(18)可渐进地识别子系统的真实状态xij。

证明选择正定的Lyapunov函数为

将V1对时间求导，可得：

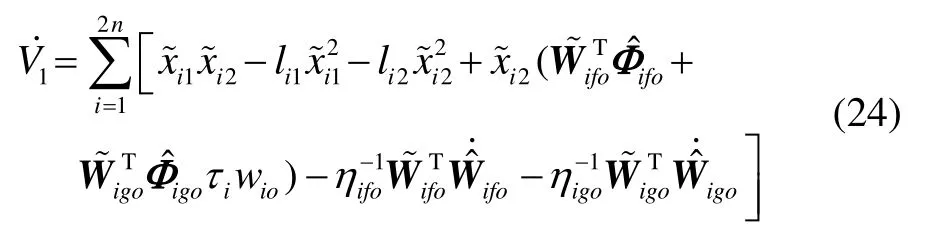
再将式(20)与(21)代入式(24)，得：

由此可知，只要不等式组(26)成立：

3 容错控制器设计及稳定性分析

3.1 容错控制器设计

定义第i个子系统的位置及速度跟踪误差分别为误差向量为，则整个闭环系统的误差向量可表示为

假设 2 关节期望轨迹xid及其导数、有界且连续。

将式(9)变换为如下形式：

式中：

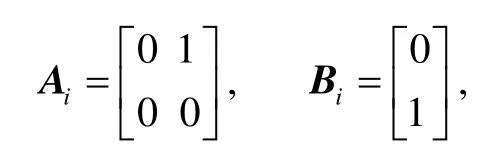
Fi为正常数。

由式(27)，可得误差动力学方程为

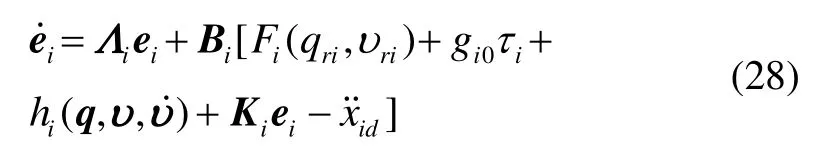
定义Pi为如下Riccati方程的解：

定义子系统的理想控制输入为

由式(30)可知，控制输入iτ*为变量riq、及ie的未知非线性函数，故其理想神经网络逼近可表示为

式中：Wiτ与Φiτ分别为理想神经网络权值和基函数；εiτ为估计误差，且满足 |ε′1i为正常数。

定义iτ*的RBF神经网络估计为

容错控制器设计为

结合式(30)(33)，误差动力学方程(24)可重写为

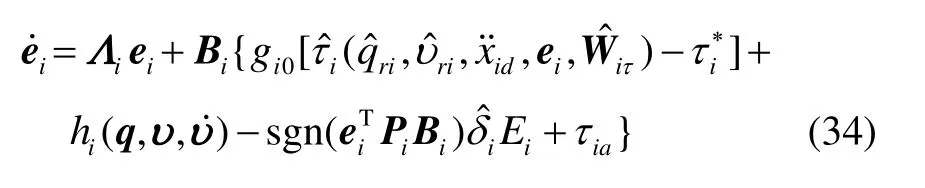
由式(31)与(32)可得神经网络估计误差为

定义神经网络的最小逼近误差为

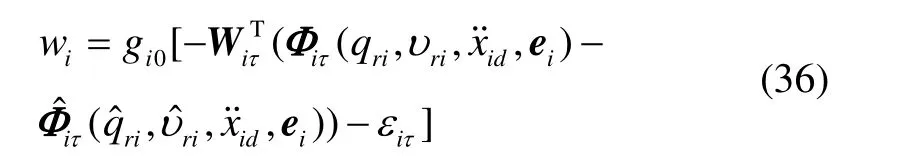
假设3 逼近误差iw满足即

结合式(35)(36)，则误差动力学方程(34)可变换为

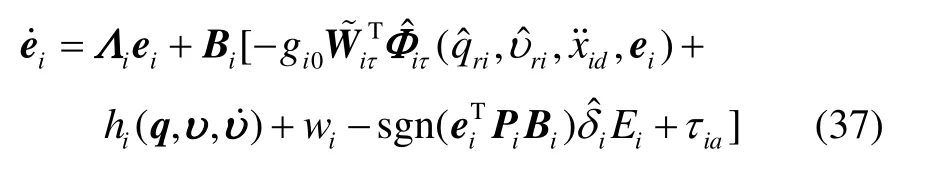
假设4 耦合交联项hi(q,υ,˙)有界且满足[11]

式中，dij为正常数。

式中，ηiτ与ηiδ为正常数。

值的注意的是，由于控制器(33)不含任何惯性参数项，因此它是一类无模型控制器。

3.2 稳定性分析

定理 2对于双臂空间机器人的故障子系统(8)，考虑假设2至假设4，并设计参数更新律(39)与(40)，则容错控制器(33)可保证闭环系统的轨迹跟踪误差e1i满足H∞收敛性能。

证明选择正定的Lyapunov函数为

将式(41)对时间求导，可得：

将式(37)代入式(42)，得：

将式(39)代入式(43)，可得：

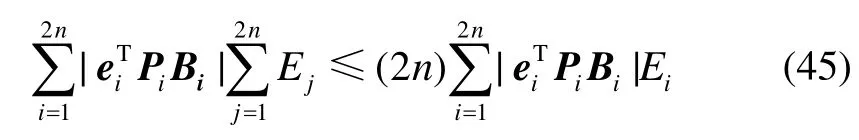
综合式(44)与式(45)，可得：

将式(40)代入式(46)，得：

由Riccati方程式(29)，可得：

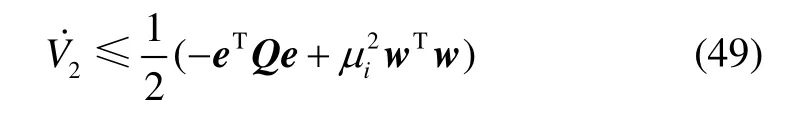
设λmin(Q)为Q的最小特征值，则有：

对式(49)从t= 0 到t= T 求积分，可得：

4 仿真对比

为了验证(33)所示的容错控制器（Fault-Tolerant Controller,FTC）的有效性，对图1所示的平面两连杆( 2)n= 双臂空间机器人系统进行数值仿真，并将仿真结果与文献[12]提出的计算力矩控制器（Computed Torque Controller,CTC）的结果进行对比。

CTC算法的表达式为

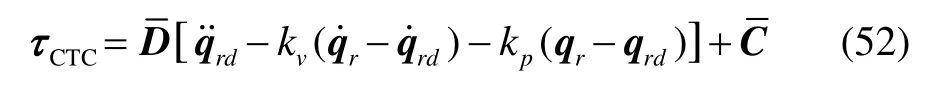
其中：qrd为关节的期望轨迹，kv与kp为正常数。

双臂空间机器人系统的惯性参数为：载体为m0= 4 0kg ，J0= 3 4kg·m2，l0=1 m；刚性臂B1与B3为m1=m3=3 kg，J1=J3=2 kg·m2，l1=l3=3m ；刚性臂B2与B4为m2=m4=2 kg，J2=J4=1.2 kg·m2，l2=l4=3 m。

状态观测器的增益为：ki1=18，ki2= 1 2，ηifo= 0 .0003，ηigo= 0 .0005。FTC算法的控制参数选取为Ki=[15,300]T，diag([80,80])，ηiτ=5，ηiδ= 2；CTC算法的控制参数为kv= 4 ，kp= 6 。RBF神经网络的基函数选择为高斯函数x为神经网络的输入变量，中心向量c均匀分布于[2,2]- ，宽度b= 2 ，隐含层节点数为5。

4.1 正常模式

此时，双臂空间机器人系统的关节执行器正常工作，即有效因子ρi=1(i= 1 ,2,… ,4 )。仿真结果如图2～4所示，其中，图2为载体姿态角位移，图3为关节轨迹跟踪曲线，图4为关节角速度观测曲线。

由图3可知，当系统的关节执行器正常工作时，FTC算法与CTC算法均能在2 s内保证关节连杆完成期望运动。由图4可知，状态观测器可对实际关节角速度信号进行精确的识别。

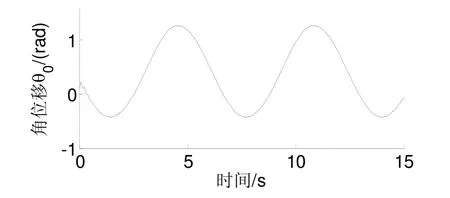
图2 载体姿态角位移Fig.2 Angular displacement of the base attitude

图3 关节轨迹跟踪曲线Fig.3 Trajectory tracking curves of the joints

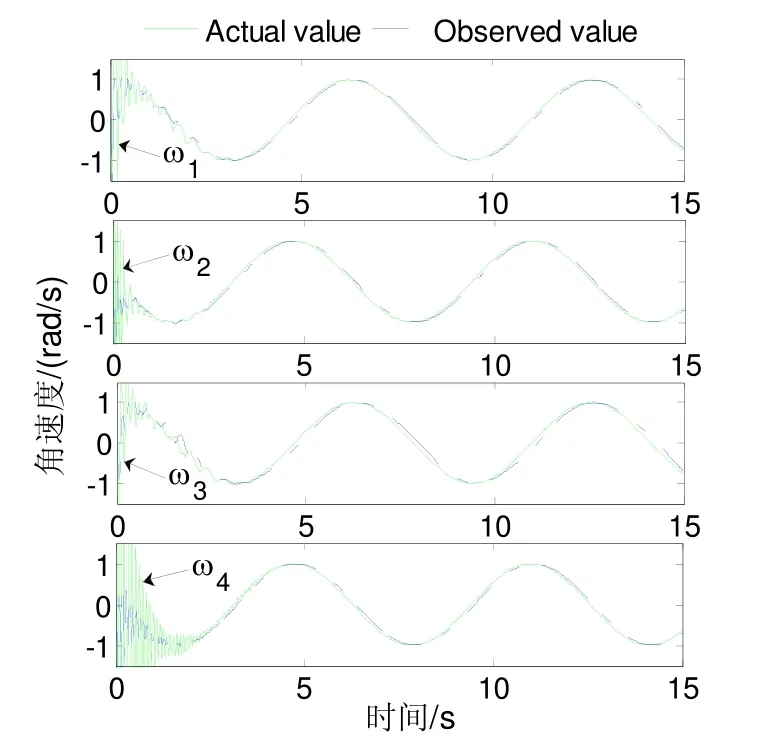
图4 关节角速度观测曲线Fig.4 Angular velocity observation curves of the joints

4.2 故障模式

假设双臂空间机器人系统右臂(B1与B2)的关节执行器在第 2 s直至仿真结束的时间段内均处于部分失效的故障状态（而在此之前正常工作），且有效因子为：ρ1=0.3，ρ2=0.5。与此类似，左臂(B3与B4)关节执行器故障发生的起始时刻为第5 s，有效因子为ρ3=0.5，ρ4=0.6。仿真结果如图5～7所示，其中，图5为载体姿态角位移，图6为关节角速度观测曲线，图7为关节轨迹跟踪曲线。

图6 关节角速度观测曲线Fig.6 Angular velocity observation curves of the joints

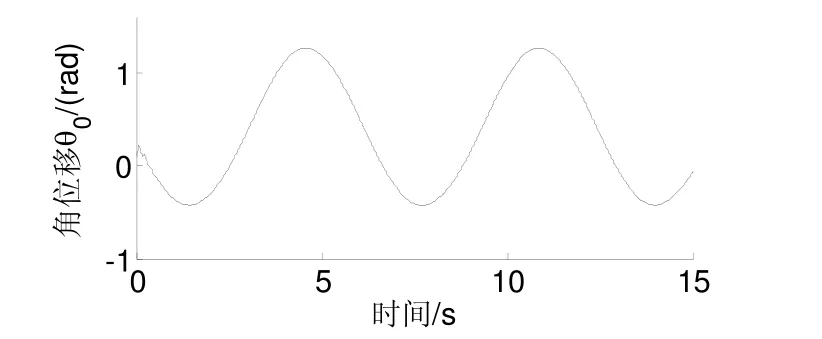
图5 载体姿态角位移Fig.5 Angular displacement of the base attitude

图7 关节轨迹跟踪曲线Fig.7 Trajectory tracking curves of the joints

由图6可知，当系统的关节执行器发生部分失效故障时，本文提出的FTC算法仍能在2 s内控制关节连杆抵达指定轨迹，CTC算法由于无法对执行器故障进行补偿，因而关节连杆的跟踪误差无法收敛。由图7可知，在执行器故障的情况下，状态观测器仍然可对实际关节角速度信号进行准确的识别。由此表明了容错控制器与状态观测器的有效性与可行性。

5 结 论

针对关节执行器发生部分失效故障、惯性参数未知且角速度不可测的双臂空间机器人，设计了一种基于状态观测器的容错控制算法。利用状态观测器对关节子系统的实际状态变量进行了识别，从而无需测量关节的角速度信号。采用RBF神经网络对子系统包含交联项、惯性参数与执行器故障在内的所有不确定非线性项进行了估计。根据预测结果在线设计容错控制器，实现了系统对关节执行器部分失效故障的容错控制。本文的控制策略同时解决了执行器故障、惯性参数未知与角速度不可测问题，具备较大的工程应用潜力，可为空间机器人的实际容错控制提供理论依据。