基于参数识别的SINS/DVL初始对准方法

徐 祥，史凡伟，徐大诚，富振铎

（1.苏州大学 电子信息学院，苏州 215100；2.北京机械设备研究所，北京 100039）

捷联惯性导航系统可以为舰船、导弹、水下航行器等设备提供全方位的导航信息。在捷联惯导系统正常工作之前，通常需要进行初始对准过程，而初始对准过程对于捷联惯导系统导航定位精度起着至关重要的作用[1]。

按照载体运动方式的不同，初始对准过程可以分为静止基座初始对准及运动基座初始对准两类[2]。其中，静止基座初始对准不考虑载体进行线运动，通常采用基于惯性系原理的姿态确定方法[4-6]。但是，这种对准方式限制了载体的运动，无法在一些机动场合较强的条件下进行初始对准，这也限制了捷联惯性导航系统的适用范围，不符合捷联惯导系统多用途、多功能的发展方向。因此，众多学者研究了运动基座上的初始对准技术。文献[7-8]介绍了一种基于 GPS速度辅助及DGPS速度辅助的运动基座初始对准技术，这为运动基座上的初始对准技术奠定了基础。考虑到水下航行器在执行任务过程中无法获取 GPS信息，文献[9-10]研究了一种基于 DVL速度辅助的运动基座初始对准方法，利用速度辅助构造惯性系矢量观测器，并通过最优基姿态确定算法完成初始对准过程。但是，该方法直接采用DVL速度构造观测矢量，这将在观测矢量中引入DVL量测噪声，导致对准结果稳定性较差。

本文在深入研究DVL辅助SINS运动基座初始对准方法的基础上，建立了观测矢量参数模型，并设计自适应 Kalman滤波算法，估计未知参数，利用估计的参数对观测矢量进行重构，实现了观测矢量的降噪，提高了初始对准的稳定性。

1 粗对准坐标系定义

1）惯性系i：选取初始对准起始时刻地球系作为初始惯性系，并且不随地球运动而改变；

2）导航系n：选取“东-北-天”为导航系；

3）初始导航系n0：初始对准起始时刻导航坐标系，并且相对惯性系不变；

4）地球系e：原点位于地心，ze轴从地心沿地球北极朝上，xe轴位于赤道平面，从地心指向载体所在子午线，ye轴与ze轴、xe轴构成右手坐标系；

5）初始地球系e0：初始对准起始时刻地球坐标系，并且相对惯性系不变；

6）载体系b：定义“右-前-上”为载体坐标系；

7）初始载体系b0：初始对准起始时刻载体坐标系，并且相对惯性系不变。

2 DVL辅助SINS初始对准

惯导系统比力方程可以表示为：

式中，fb表示比力，gn表示地球重力加速度在导航系的投影。

由方向余弦矩阵的链式法则可知：

将式(2)代入式(1)可得：

由坐标变换可知：

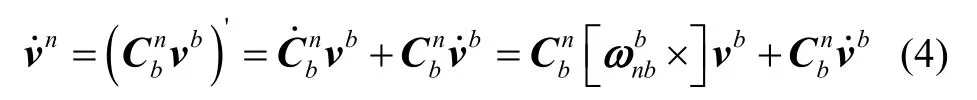
将式(4)代入式(3)，并对等式两边积分可得：

其中，

由于DVL采样时间与SINS采样时间不一致，此处假设DVL采样时间为Δtd，SINS采样时间为Δts，并且有 Δtd=SΔts（S∈ ℜ+） 。考虑到观测矢量的计算方式，以DVL量测更新时刻计算离散化矢量。

求解观测矢量：

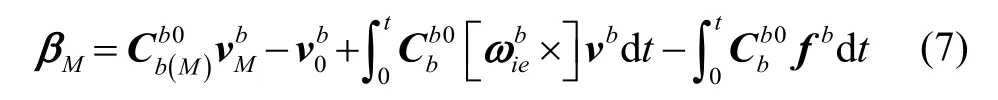
式中，t=MΔtd，并以M进行简化表示。式(7)中，为小量，可以忽略，且等号右侧第二项积分可以计算为

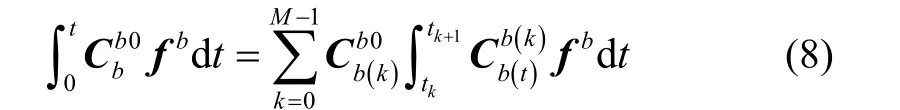
式中：tk=kΔtd，并以k进行简化表示；

由文献[8]可知：

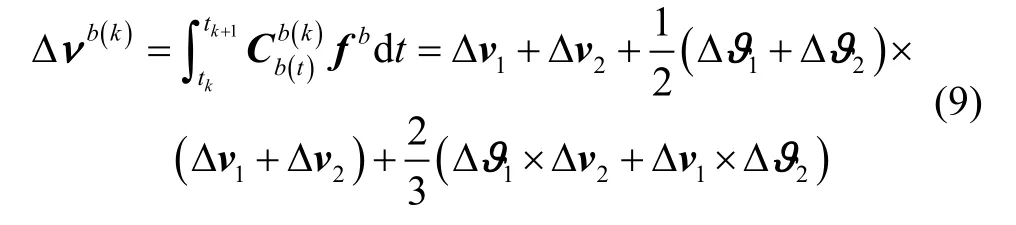
因此观测矢量可离散化计算为：

同理，参考矢量可以计算为：

考虑到初始对准过程中，载体运动速度较慢，运动范围较小，由文献[10]可知，可以采用初始时刻的来替代

考虑DVL与SINS之间的安装误差角及比例因子误差均得到标定并补偿，此时DVL量测可以表示为：

将式(12)代入式(10)可以得到利用DVL量测计算的观测矢量：

由式(13)可以看出，观测矢量易受DVL量测噪声的影响，并最终导致估计姿态呈现噪声特性。为解决该问题，下面将通过设计参数识别算法，实现矢量的重构，减小DVL噪声对初始对准结果的影响。

3 运动基座速度视运动建模

由观测矢量的计算表达式可知：

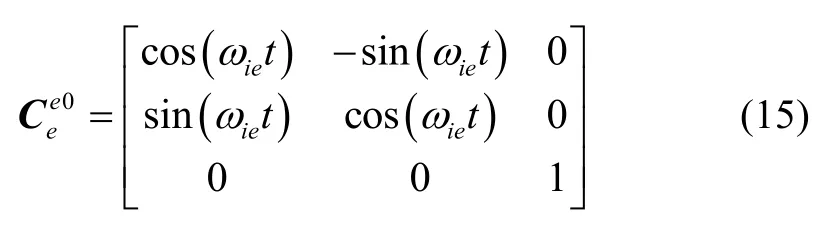
因此，α可以计算为：

式中，Φ表示常值矩阵，Γ（t） 表示为：

由式(5)可知：

式(18)给出了不含噪声情况下的观测矢量的表示形式。但在实际情况中，计算的观测矢量式(13)含有DVL量测噪声及惯性传感器量测噪声，这会干扰对准的收敛速度及准确性。为此，本文将基于式(18)的参数模型，对未知参数矩阵进行估计，利用估计的参数矩阵进行观测矢量重构，实现降噪过程，提高对准性能。

4 参数估计与矢量重构

由式(10)(13)和(18)可知：

假设观测矢量三个通道之间不存在相互耦合，以z轴为例进行参数估计。参数模型为：

在实际情况中，观测矢量噪声中除 DVL量测噪声外，还包含惯性传感器的量测噪声，这将导致观测矢量噪声统计不准确。为克服这个问题，本文采用自适应 Kalman滤波算法对未知参数进行估计，具体流程如下所示：

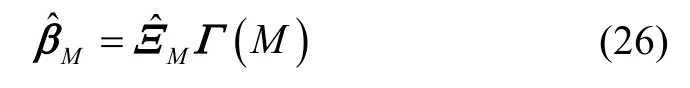
根据上述重构矢量，可以计算：

式中，

其中，[· ×]表示矢量对应的斜对称矩阵。

由四元数最优基方法可知[8]，最小特征值对应的特征矢量即为当前时刻估计的最优姿态四元数由姿态四元数与方向余弦矩阵之间的转换关系，结合方向余弦链式法则式(2)，即可得到当前时刻的方向余弦矩阵从而完成初始对准。

5 实验与分析

5.1 仿真实验

为验证本文提出的算法，本节设计了仿真实验，将本文设计的算法与传统方法（文献[10]）方法进行对比，从算法的收敛速度和对准精度两个方面进行验证分析。

仿真实验过程中，传感器误差参数设定如表1所示。设定惯性传感器数据输出频率为200 Hz，DVL数据输出率为1 Hz，DVL量测噪声设置为0.1 m/s。

表1 传感器误差设定Tab.1 Sensor errors setting

载体运动轨迹及状态如图1和图2所示。运动过程持续300 s，运动过程中载体进行转向机动。

图3为观测矢量与重构矢量效果图。从图中可以明显的发现，采用参数识别之后，重构观测矢量的噪声明显小于直接计算得到的观测矢量噪声，这也是本文算法具有抑制DVL量测噪声的原因。

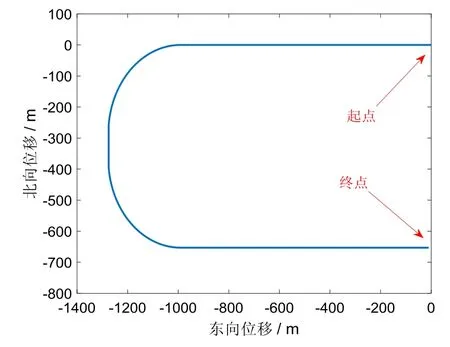
图1 载体运动轨迹图Fig.1 In-motion trajectory of the vehicle

图2 载体运动状态图Fig.2 In-motion status of the vehicle

在上述仿真条件下，得到仿真结果如图3～6所示。

图3 观测矢量与重构矢量Fig.3 Observation vector and reconstructed vector

图4～6分别表示纵摇角、横摇角和航向角的对准误差曲线。从图4和图5可知，传统方法对准误差呈现波动特性，尤其在对准过程的起始阶段。采用参数识别方法，误差的波动特性明显减小。两种方法的对准误差在300 s左右可以达到相同的对准精度，误差角小于0.01°。图6的航向角对准误差表明，传统方法易受DVL量测噪声的影响，导致对准结果呈现波动特性，而采用参数识别之后对准误差更加稳定。不同于水平姿态误差，航向姿态角误差易受观测矢量噪声影响，从而在整个对准过程中，传统方法对准误差的波动性大于参数识别方法，这可以从图6的局部放大图中发现。对航向误差角进行200～300 s之间进行误差统计可知，传统方法的标准差为0.23°，而参数识别方法的标准差为0.1°左右，这也进一步验证了参数识别方法的优势。

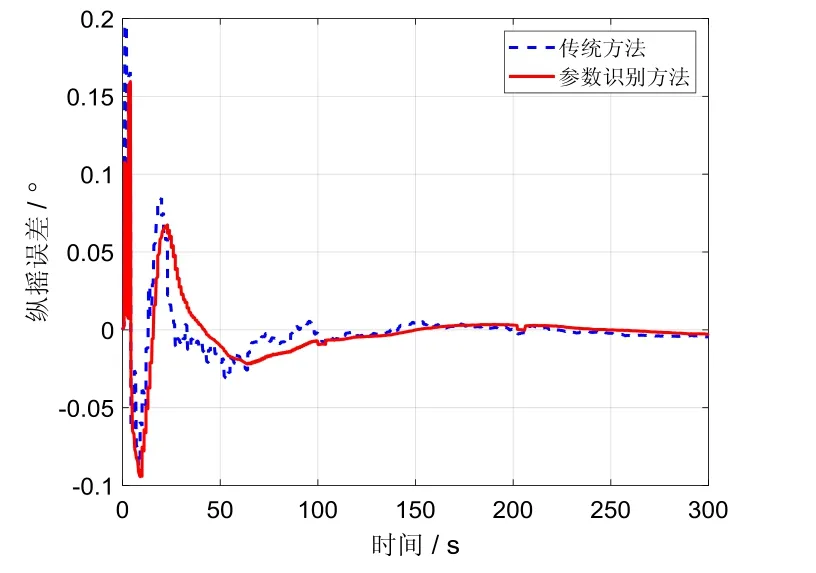
图4 纵摇误差Fig.4 Errors of pitch

图5 横摇误差Fig.5 Errors of roll

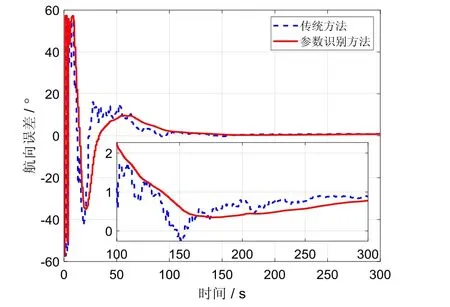
图6 航向误差Fig.6 Errors of yaw

5.2 跑车实验

为验证本文提出的算法，现设计跑车实验进行验证。实验过程中采用光纤捷联惯性导航系统，其陀螺仪和加速度计性能参数参见表2所示。

表2 传感器特性Tab.2 Sensor errors

惯性传感器采样频率为200 Hz。采用NovAtel GPS接收机输出的BESTVEL Doppler 速度输出指令模拟DVL载体系速度，其速度采样频率为1 Hz。在对准之前，系统工作在GPS与惯导组合导航模式下，并以GPS和惯导组合导航系统姿态作为参考姿态与对准结果进行标校。

载体运动轨迹如图7所示。

图8为观测矢量与重构矢量效果图，从图中可以看出，采用参数识别方法可以减小DVL噪声对观测矢量的影响，从而提高对准结果的收敛速度。

图7 载体运动轨迹图Fig.7 In-motion trajectory of the vehicle

图8 观测矢量与重构矢量Fig.8 Observation vector and reconstructed vector

图9～11分别为纵摇角、横摇角和航向角对准误差曲线图。从图中可以看出，采用参数识别算法之后，对准曲线收敛速度更快，这一结果在对准前100 s更为明显。在对准精度方面，两个水平姿态误差角对准精度相似，均可以收敛在0.02°以内。而航向角误差方面，采用参数识别算法具有更快的收敛速度，且对准稳定性更优。

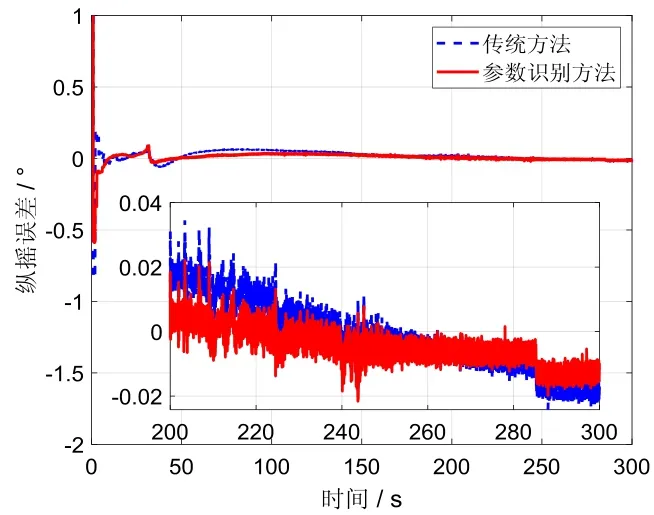
图9 纵摇误差Fig.9 Errors of pitch

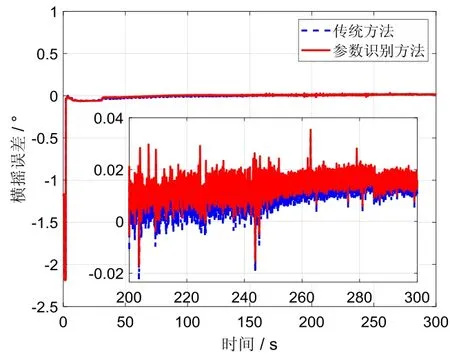
图10 横摇误差Fig.10 Errors of roll

图11 航向误差Fig.11 Errors of yaw

6 结 论

针对传统DVL速度辅助SINS行进间初始对准易受 DVL量测噪声影响的问题，本文研究了一种基于参数识别方法的行进间初始对准方法。通过研究SINS/DVL初始对准观测矢量，构建了参数识别模型，并对参数进行估计，从而重构观测矢量，减小噪声的影响。通过设计仿真与跑车实验，验证了本文设计的方法比传统方法具有更高的稳定性。