基于叶端定时的转子扭转振动监测方法及系统研究*
2019-07-23翟功涛王维民陈子文
翟功涛 王维民 陈子文 邵 星
(北京化工大学高端机械装备健康监控与治愈化北京市重点实验室)
0 引言
扭转振动是旋转机械轴系的一种基本振动形式,其产生原因是轴系旋转过程中来自外部或内部的力矩发生变化,如驱动力矩,交变负载力矩变化等[1]。近年来,由于变频电机的大量应用,一方面变频器会产生大量的谐波激励,再一方面转速的变化使得工作转速容易接近扭转临界转速,从而使得扭转振动导致的故障及事故更加突出。图1为轴系扭振造成的疲劳裂纹[2]。

图1 扭振造成的疲劳断裂Fig.1 Fracture caused by torsional vibration
扭振的测量就是要获得旋转轴因交变力矩引起的角速度变化或测量点的弧长变形(或扭角)及扭振角频率的变化规律[3]。现阶段,随着科技的进步和轴系扭振原理研究的不断深入,轴系扭振监测的方法和设备都有了很大的进步,扭转振动测量[4]也发展到了一个成熟的阶段。但扭振信号的拾取精度、数据分析方法的有效性、扭振监测系统的实时性都亟待进一步的提高,尤其在复杂的工业环境中,如何便捷、准确的进行扭转振动的测量是目前需要继续研究的问题[5-6]。而随着大型机组结构的日趋紧凑化,开发新的扭振测量方法和多功能一体化的测试系统就显得尤为重要。现在旋转机械测量扭振的方法按照信号的获取方式一般可以分为直接测量法和间接测量法,直接测量法按照传感器是否与被测轴接触又能分为接触法和非接触法。接触测量法获得旋转轴扭振信号的方式是通过在被测轴上安装传感器,扭振信号通过电滑环外接引线或者无线的方式来传递扭振信号。非接触法测量可分为测齿法和新发展的激光测量法。测齿法主要包括相位差法、频率计数法和脉冲时序计数法[7]。旋转编码器是这类测量中精确度最高的设备,通常使用适配器连接到旋转轴自由端。间接测量法主要用于传感器不易安装的环境,定子电流法[8]就是其中的一种。在转轴发生扭转振动时,电机定子的电流的幅值会被扭振信号调制,通过电信号进行频谱分析和电流信号的解调分析,得到被测轴的扭振特性信息[9-10]。
本文研究的内容是在叶端定时法监测叶片振动的基础上,开发轴系扭转振动的测量算法。系统利用叶片振动监测设备实现对轴系扭振的测量,丰富了设备的功能,提高了实验的效率。通过模拟仿真和实验验证两种方式确定该方法在实际测量中有效可行。
1 扭振测量基本原理
扭转振动测量的方法中,脉冲时序计数法实施简便、可行性和测量精度均较高。本系统采用的是非接触测量法中的脉冲时序法。系统基于叶片振动测量的硬件设备开发设计,等分的叶轮叶片可以产生理想的脉冲信号,所以选用脉冲时序计数法最为合适。测量结构如图2所示:

图2 脉冲时序计数模型Fig.2 Pulse timing counting model
在被测轴上有等分机构的情况下将传感器正对等分机构安装,再确定一个凸起或凹陷作为键相,传感器对准等分机构和键相安装,用以获得脉冲信号。实验测试基于叶端定时法[11-12],利用叶片振动监测实验台现有硬件设备监测轴系的扭振。其基本原理为通过测取叶片脉冲序列得出叶片实际的到达时间与理论到达时间的差值来反映轴系的扭振大小。系统的扭振测量原理如图3所示:
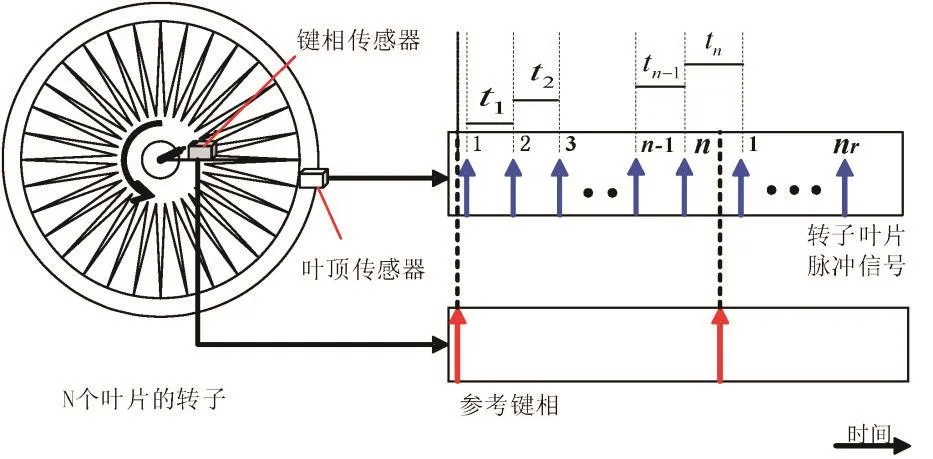
图3 扭振测量原理图Fig.3 Schematic diagram of torsional vibration measurement
当轴系不发生扭转振动时,相邻叶片到达的时间差相同。轴系发生扭振时,每个叶片的到达时间发生变化,超前为正滞后为负,导致相邻叶片的实际到达时间差发生改变,这个差值就反映了扭振的变化,再将时间差值经过相应的换算就能获得轴系扭振的角位移。因此,只要测出每相邻叶片之间的脉冲时间差的变化,就可以得到轴系的扭振。
1.1 叶片厚度加工误差影响分析
实际叶片厚度存在加工误差,即使轴系无扭振,也会导致叶片到达时间的差异,从而影响扭振大小。所以不妨先进行一番假设,假定叶片的厚度存在误差,通过计算分析其对叶片扭转角速度的影响。验证如下:
本实验台叶轮直径D=138mm,叶顶周长C=138πmm,叶片个数Z=32。设轴系平均角速度ωr=157.1rad/s,假设某叶片此时叶尖扭振位移弧长为L=0.1mm(此叶片无加工误差)。计算当叶片厚度加工误差为20μm对此时扭振大小的影响。叶片厚或薄反映到扭振位移的数值上只是正负的区别,对误差影响的百分比无影响。为了方便计算,假设此误差使得叶尖扭振位移弧长增加了20μm。即具有加工误差的扭振位移弧长:
L1=0.1+0.02=0.12mm
经过每两个叶片时间tT为:
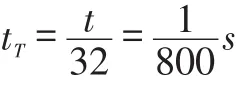
扭转角速度ωt为:

当叶片无误差时扭转角速度ωt0为:
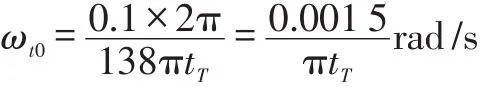
叶片厚度误差为20μm时扭转角速度ωt1为:
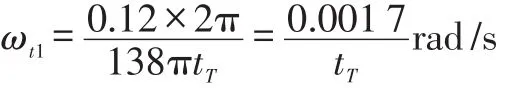
因为扭振信息可以分解为一系列频率和幅值不同的简谐分量,所以被测轴截面的角位移可以表示为:
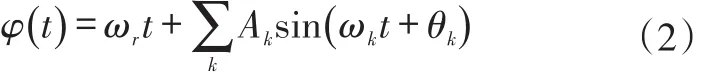
式中Ak,ωk和θk分别代表在第k个简谐分量中,振动的幅值、角频率和振动的初始相位。所以此时转轴的瞬时角速度ω为平均角速度和扭振角速度的迭加:
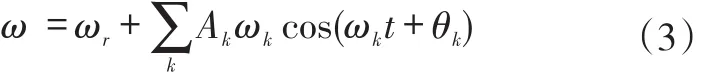
无加工误差和加工误差为20μm的叶片的瞬时角速度ω0,ω1分别为:


表1 叶片厚度误差对扭振大小的影响Tab.1 The influence of blade thickness error on torsional vibration
由表1中 ωt0,ωt1结果对比可知,当角速度为157.1rad/s时,编号2存在20μm加工误差的叶片相较于无加工误差的编号1造成扭转角速度差0.05rad/s,误差为0.05/157.48=0.03%,远小于0.1%。所以微小的加工误差对扭转角速度的影响忽略不计。视叶轮叶片厚度相同,相邻叶片之间弧长相等。恒速下无扭振时,每相邻叶片的脉冲时间间隔相同。
1.2 叶片振动对扭振测量的影响分析
本扭振测量系统是基于叶端定时法,需要分析叶尖周向振动对扭振大小的影响。下面通过MATLAB建立转速波动方程来模拟仿真叶片振动对扭振测量的影响。
1.2.1 轴系扭转振动模型建立
由于扭振的存在,即使在平稳工况,轴系的转速也不是一个恒定的值,它还包含由扭振引起的转速波动成分,在平稳工况下轴的瞬时角速度表示为:

建立由扭振引起的转速波动方程ωt为:

其中,平均角速度为ωr=219.9rad/s,转速波动幅值rad,转速波动频率5.4Hz,即:
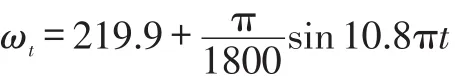
对扭振引起的转速波动方程ωt作图,得图4。

图4 扭振引起的转速波动方程Fig.4 Rotational speed wave equation caused by torsional vibration
对公式(5)积分得到扭转振动角位移θt:

即:

1.2.2 叶尖周向振动模型建立
对于单自由度叶片的振动模型,可以通过MATLAB中的Simulink模块进行建模仿真。在单自由度振动系统中叶片之间无耦合,通过对单个叶片进行仿真分析来研究整体叶片的振动情况。叶片的仿真模型参数设置如表2所示。

表2 叶片参数设置Tab.2 Blade parameters setting
根据表2建立以角速度表示的叶尖周向振动方程为:

将振动方程ωT对t进行积分得到振动角位移表示的振动方程θT:

1.2.3 叶尖振动关联轴的扭转振动模型的建立
在前两小节已经分别建立了轴系扭转振动模型和叶尖周向振动模型,现将两个振动模型的振动角位移方程叠加,得到一个叶尖周向振动关联轴扭转振动的角位移方程θk。
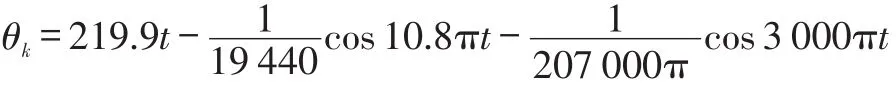
将上式得到的θk标定为第一个叶片的振动角位移方程θk1,即θk1=θk。叶轮的32个叶片间隔相等,每相邻叶片相隔等间距θj:

第i个叶片的振动角位移方程θki表示为:

即:

当θki=2kπ时求得的值即为第i个叶片在第k圈经过传感器的脉冲时间tki。其中i表示叶片编号,k代表叶片转过的圈数,即令:

分别画出θki,θ=2kπ的方程曲线(注:图5中曲线包含波动转速成分),并截取k=1、k=2时两曲线相交的部分,如图5所示。

图5 模拟仿真叶片脉冲时间序列Fig.5 Simulated blade pulse time series
两曲线的交点表示脉冲时间tki,通过两方程联立我们得到了叶端脉冲时间序列的矩阵tki:

为了分析叠加叶尖周向振动对转速波动曲线的影响,需要将此时间脉冲序列带入本小节开始建立的转速波动方程(5)中。利用MATLAB行列变换将式(8)的矩阵tki按照列元素排列,首尾相接拉直生成一行新的时间脉冲矩阵tik:

新的脉冲时间矩阵tik为叠加叶尖周向振动后轴系扭转振动方程的叶端时间脉冲序列。与本系统实验采集叶端脉冲信号的时间序列相对应。可以直接将其带回转速波动方程(5)中,得到一个新的转速波动曲线图,将其与最初建立的转速波动曲线对比,即能反映叶片振动对扭振测量的影响。
如图6所示,红色转速波动曲线1表示叠加了叶片振动的转速曲线,蓝色转速波动曲线2表示因扭振引起的转速曲线,图6中两条曲线重合,并没有明显的差别。需要将其进一步放大分析。截取图中黑色方框中的曲线放大如图7所示。
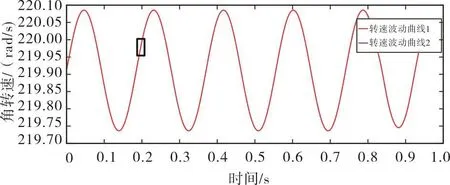
图6 叠加叶片振动的转速波动曲线Fig.6 Superimposed blade vibration speed fluctuation curve

图7 转速波动曲线放大图Fig.7 Enlargement of rotation speed fluctuation curve
由图6和图7可知,两条曲线相差很小,其差值远远小于转速波动曲线本身的幅值。即叶尖周向振动的叠加对转速波动影响很小,远小于因扭振引起的转速波动的幅值,可以忽略。
结论:叶尖周向振动对扭振测量的影响可以忽略,也验证了本文基于叶端定时的转子扭转振动监测方法和系统的可行性。
2 基于叶端定时的扭振测量方法
分析了各误差的影响,接下来就通过叶轮32个叶片的脉冲信号分析轴系扭振。
以第一个叶片信号到来的时刻作为第一个计数点,如图8所示,叶尖信号的理论达到时间为无扭振状态下的脉冲计数,测得相邻两个叶片之间的时间间隔tbn(n=1,2,3…32)。由于相邻两叶片间隙相同,所以在恒速下tb1=tb2=…=tbn,由于此时轴系未发生扭振,所以tbn为相邻叶片脉冲时间的基准数据。设轴旋转k周的时间为T,平均角速度为ωr=2kπ/T。若轴发生扭转振动,则每相邻两个叶片的脉冲时间差相对于基准数据tbn会发生很小的变化Δtn:


图8 本系统扭振信号脉冲原理图Fig.8 The system torsional vibration signal pulse schematic diagram
角度计算公式为:

其对应的角度变化为:
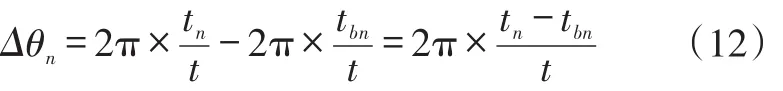
又因为:

所以:

式(14)计算得到的角度变化Δθn为叶片n相对于前一个叶片n-1发生的角度变化,第n个叶片的角位移θn为前n个叶片发生的角度变化之和,即:
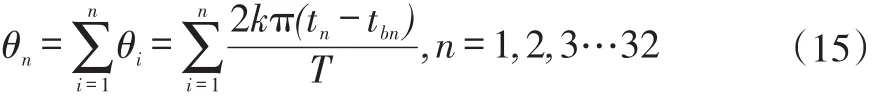
根据式(15),就可以计算得到每个叶片相对于第一个脉冲起点的角位移,即扭振幅值的大小。
3 实验研究
3.1 系统硬件的设计
为了减少叶片振动对轴系扭振的影响,实验中使用高速刚性直叶片振动实验台,具体结构和细节如图9所示。实验台主要由底座、支撑体(电机包含在内)、操作平台、测试叶轮、护罩及其他辅助元部件组成。

图9 高速刚性直叶片实验台Fig.9 High-speed rigid straight blade test bench
扭转振动测试实验台中使用的光纤传感器为六合一光纤。测试系统采用5通道激光源(1通道用于键相、4通道用于叶尖计时),光功率可在0~1.2W连续调节。使用独立供电的光电转换器,支持最大带宽为150MHz,满足一般扭转振动测量要求。采用基于FPGA的高速数据采集系统Compact-RIO,可实现20MS/s的数字采样。采集器的计数时钟频率5MHz,工频转速为50Hz的情况下,仪器的角分辨率Dn为:
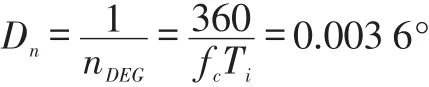
式中,fc表示采集器计数时钟频率,Ti表示旋转周期。具体方法是,激光源发射激光打到叶片上,安装在叶顶的光纤传感器接收到每个叶片反射回来的光脉冲信号,通过光电转换器转换成电信号进入滤波板,进行噪声滤波。经过噪声滤波之后的信号进入到NI高速采集板卡,转换为数字量后进行分析处理。
本测试系统开发的目的是集轴系扭转振动、叶片振动、叶顶间隙等测量功能于一体。为满足与设备良好的交互感,更好的隔绝各设备之间信号干扰,提高各实验切换的效率,专门设计并制作了多功能一体化控制柜,一体化设计体现在所有测试设备都集中布置在一个控制柜中。实验中下位机监测与上位机控制可以同时在一台控制柜上进行,实现了监控一体化,满足了良好的人机交互,大大减少了实验空间,使测试系统更加的高效。具体结构及制作细节见图10。

图10 测控一体化控制柜Fig.10 Integrated measurement and control cabinet
3.2 系统软件的设计
图11 为轴系扭转振动监测系统简图。
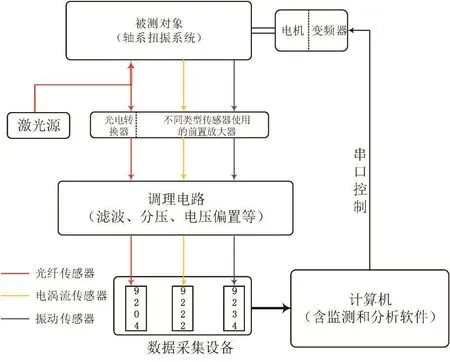
图11 扭转振动监测系统简图Fig.11 Torsional vibration monitoring system diagram
本系统能根据需求进行功能性扩展,可对轴系扭振、叶片振动、叶顶间隙、横振以及轴向位移进行监测。系统需同时接入光纤传感器和电涡流传感器。前者用于轴系扭振和叶片振动监测,后者用于叶顶间隙测量和轴向位移监测[13-15]。本文只讨论轴系扭转振动,测试系统只保留光纤传感器监测部分。使用光纤传感器监测轴系扭振的主要原因是光纤传感器较其他传感器响应速率最高,随着转速的升高也能准确捕获叶片到达的时间。
测试系统中数据采集和分析程序均为本实验独立开发,图12为监测系统程序框架图。包含电机转速控制程序、数据采集程序、叶片理论到达时间标定程序、扭转振动位移分析程序、数据处理-拟合和数据后处理六个模块。
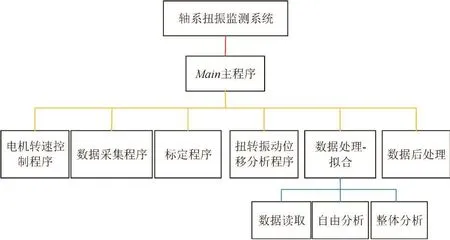
图12 测试系统程序框架图Fig.12 Program framework of test system
系统软件基于Labview平台进行设计,来自传感器的脉冲信号先进入信号处理板过滤噪声干扰,再经下位机Compact-RIO采集器传入PC端Labview的数据采集程序。测试分析程序通过转速计算模块分析叶片连续的脉冲信号得到转速曲线,同时叶端定时模块可得到每相邻叶片实际到达时间差。实际到达时间差需要减去基准数据。因为随着转速的不断升高,每相邻叶片的实际到达时间缩短,所以不能选取相邻叶片时间差较平稳的一段作基准数据。于是本系统在数据处理-拟合模块将相邻叶片实际到达时间差的数据进行多项式曲线拟合处理,得到与计算的数据长度相同的一条拟合曲线。这条拟合曲线随着转速上升而下降,且数值稳定可作为基准数据。
因为数据长度为22 398,本系统取整设置多项式阶数为20 000(曲线拟合子vi的属性规定:多项式阶数越大拟合值越接近,但阶数不可大于n-1,n为数据长度)。在数据后处理模块将叶片实际到达时间差与基准数据相减得到一个时间差,即为扭振引起的叶端到达时间偏差。软件前面板即可呈现连续的扭振角随时间变化图表,并通过傅里叶变换将时域图转化为频谱图。从而实现了基于叶端定时的转子扭转振动监测及相关分析。
4 实验验证
为验证本系统的准确性,本文对第2小节实验研究中的数据进行MATLAB数据处理计算扭振,将实验测试分析得到的扭振与MATLAB计算的结果对比,验证软件设计的准确性和可靠性。
MATLAB数据处理计算扭振是通过分析轴系转速波动变化反应扭振大小。叶轮在轴的周向等分为32个叶片,每个叶尖的脉冲信号都携带着转速波动的成分。通过32个叶片的脉冲序列得到转轴的转速曲线,将其叠加。再减去通过键相数据得到的一条作为基准的转速曲线,获得转速波动的大小。即反映了轴系发生扭振的幅值。将MATLAB扭振数据处理得到的全叶片转速曲线与实验得到的转速曲线作对比如图13(a)、13(b)所示。
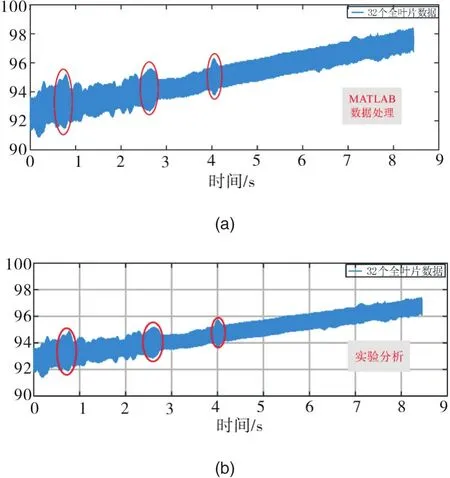
图13 转速曲线Fig.13 Speed curve
由上图中转速曲线(a),(b)中上下红色圆标记对比可以发现,两种工具的不同算法得到的转速曲线同时在0.7s,2.7s,4.1s附近发生较大的转速波动,且整体波动趋势相同。转速波动是扭振的一种表现,在其附近相应的扭振值也会突变。图14(a),14(b)是扭振角位移随时间变化的对比曲线c,d。我们亦发现在曲线c,d中标记的几处扭振值突变的时间正是在图13和图14中0.7s,2.7s,4.1s附近,且(a)、(b)两曲线的横纵坐标都能对应。综上,本系统和MATLAB数据处理计算扭振两种不同的算法得到的转速曲线和扭振角位移曲线高度吻合,即验证了本测试系统软件设计的准确性。
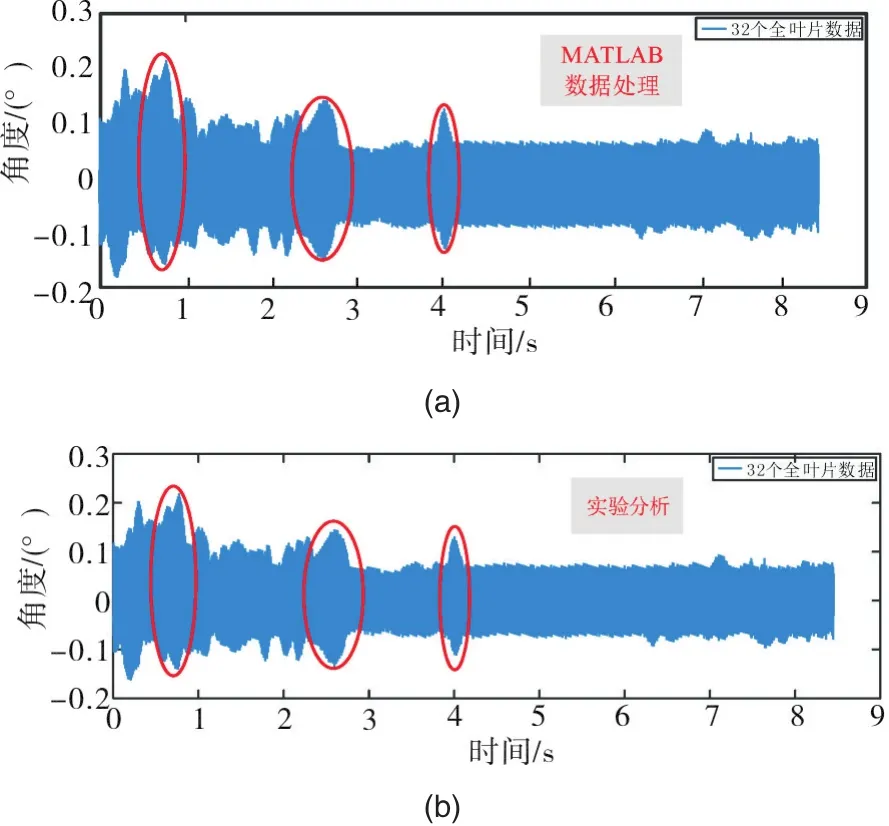
图14 扭振角位移Fig.14 The angular displacement of the torsional vibration
如图15所示,MATLAB数据处理选取了转速从94Hz到95Hz中很短一段(视为在恒转速94.5Hz附近波动)扭振信号时域图做傅里叶变换对比分析,得到的频谱图的基频为94.72Hz,幅值为0.003°,而幅值最高的为14倍频频率为1 326Hz,幅值为0.025°。频谱图如图16。
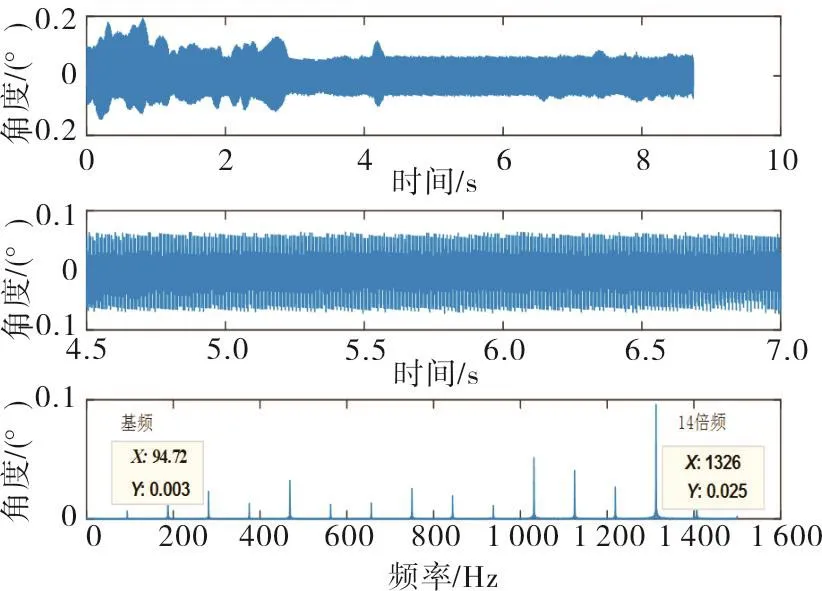
图15 选取94-95Hz数据做FFTFig.15 Select 94-95Hz data as FFT

图16 MATLAB数据处理计算频谱图Fig.16 MATLAB data processing calculation spectrum
对比监测系统计算相同时间段的频谱图17,基频94.66Hz,幅值0.003°,幅值最高依然是14倍频,频率为1325.1Hz,幅值0.025°。与MATLAB扭振数据处理的数值完全对应,所以通过频谱图信息对比再一次验证了本系统的准确性和可靠性。

图17 监测系统计算频谱图Fig.17 Monitoring system calculates spectrum
综上,本文开发设计的基于叶端定时的转子扭转振动监测方法及系统可行,且准确度较高。系统为生产中的大型旋转机组难以安装过多的监测设备提供了思路和解决办法,更丰富了不同工况下扭转振动测量的方法种类。
5 结论
目前大型旋转机械机组结构设计越来越复杂紧凑,安装各类监测设备愈加困难,适用于大型机组的监测设备功能集成化也成了科学生产发展的必然趋势,设计一种能实现多功能采集的监测设备更受欢迎。
针对现有的扭振监测设备不便在旋转机组中安装的实际问题,本文结合叶轮叶片振动测量的硬件及仪器设备,开发了基于叶端定时时法的转子扭转振动监测方法及系统,经验证:
1)本系统可以实现监测轴系扭转振动、叶片振动、叶顶间隙、轴向振动等多种参数的测量。
2)本系统测量得到的转速曲线、扭转角位移、频谱等图表与MATLAB扭振数据处理计算相应图表对应,证明系统算法的准确性。
3)本系统采用的Compact-RIO采集器可提供5MB的采样频率(受限于Compact-RIO的时钟频率,采集数字量的采样率只能达到40MB),扭转角分辨率达到60000/5000000=0.012°。而当选取最高采样率40MB时,扭转角分辨率更是达到了0.0015°。满足了系统的高精度。
本系统为将来进一步在工业环境中开展轴系扭转振动的实时监测、分析报警、故障分析及寿命评估等功能提供了理论基础和实践平台。
