基于Monte Carlo法和积分法的被动永磁轴承磁力计算
2019-07-23李维程文杰肖玲钟斌李明
李维,程文杰,肖玲,钟斌,李明
(西安科技大学 a.理学院;b.机械学院,西安 710054)
被动永磁轴承利用永磁体环产生磁力和刚度,实现转子悬浮,不需要外界输入功率进行控制,相对于主动电磁轴承,被动永磁轴承结构简单,具有很高的鲁棒性[1]。根据Earnshaw规则,被动永磁轴承不可能自发地获得一个稳定的平衡点,即对于径向被动永磁轴承,需要对轴向位置进行控制,而对于轴向被动永磁轴承,则需对其径向位置进行控制[2]。另外,被动永磁轴承的阻尼非常小,这种低阻尼、负刚度的特性使其受到的关注较少。然而,被动永磁轴承的承载力和刚度可以通过采用堆叠结构获得较大提升,如今随着高磁能积永磁材料的发展,其在工业领域获得了越来越广泛的应用,比如高速压缩机[3]、风力发电机[4]、储能飞轮[5]。文献[6]采用径向箔片轴承及轴向被动永磁轴承结构实现了转子在40 000 r/min转速下的完全稳定悬浮。文献[7]对被动永磁轴承并联油润滑滑动轴承的稳态承载力分配进行了研究。最简单、典型的被动永磁轴承是由2个永磁环构成,其中一个固定在定子上,另一个随转子旋转。这种结构的磁力一般有2种解析法,即偶极子法和等效磁荷法(库仑模型),偶极子法适用于永磁体尺寸不大于气隙尺寸的情形;等效磁荷法适用于永磁体尺寸大于气隙尺寸的情形[8]。此外,可以利用磁路法求解这种典型被动永磁轴承的磁场分布及刚度[9-10]。文献[11]研究表明,对于轴向充磁的径向永磁轴承,当定子为180°的半环时承载力最大。采用等效磁荷法获得的轴承磁力表达式涉及到四重积分,且难以获得解析表达式,文献[12]采用MATLAB软件中的梯形积分法进行求解,文献[13]采用Monte Carlo法计算永磁轴承磁力,文献[14]专门针对轴向充磁的径向永磁轴承,给出了一种基于系数拟合的轴承磁力解析解,使设计更为简便,但对于其他类型的轴承不适用。文献[12]研究了轴向磁化、径向磁化和垂直磁化下的堆叠型被动永磁轴承的刚度数学模型,涉及到大量积分、求和运算;文献[15]提出了堆叠型径向永磁轴承的刚度、峰值磁力解析式,涉及到指数、求和运算。
为了更简便、直观地获得四重积分的数值解,可以离散轴承计算区域,将积分转换为求和运算,划分的单元数越多,计算结果越准确,但计算速度将变慢。当采用Monte Carlo法求解时,计算速度也会随样本点数目增多而下降,但计算结果更准确。现以一种半定子环轴向充磁径向永磁轴承为例,分别采用数值积分法(采用MATLAB软件中的四重for循环实施)和Monte Carlo法进行求解,对比2种方法的计算结果和时间。另外,现有文献对堆叠型永磁轴承磁力的求解略显复杂,不利于工程中应用,为此,将轴承模块化,提出一种方便、准确的堆叠型永磁轴承磁力计算方法。
1 被动永磁轴承磁力数学模型
半定子环轴向充磁径向永磁轴承实际上是轴向充磁径向永磁轴承的一种特殊情况,其力学模型如图1所示。图中,O1和O2分别为定子和转子坐标系原点,且yz平面均建立在定子左端面2上;R1,R2分别为永磁体环的内、外半径;R3,R4分别为定子环的内、外半径;l为磁环宽度;e为O2相对于O1的偏心距;x0为内磁环相对于外磁环的轴向位移;r2为P相对于O1的位矢长度;r3为Q相对于O2的位矢长度;r0为Q相对于P的位矢长度;α为Q在O2yz坐标系中的角度坐标;β为P在O1yz坐标系中的角度坐标。根据其磁化方向,磁荷分布于外磁环环面1,2和内磁环环面3,4上,定子环面上磁荷微元P与转子环面上的磁荷微元Q之间相互作用形成磁力。

图1 半定子环轴向充磁径向永磁轴承力学模型
根据等效磁荷理论,内、外磁环间磁力分别在3个坐标轴方向上的分力为

r2r3dr2dr3dαdβ,
(1)
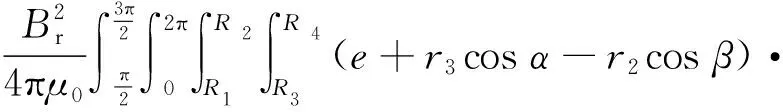
(2)
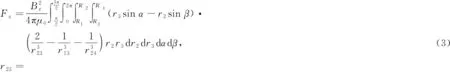
(r3sinα-r2sinβ)2]1/2,
r24=[(l+x0)2+(e+r3cosα-r2cosβ)2+
(r3sinα-r2sinβ)2]1/2,
r13=[(l-x0)2+(e+r3cosα-r2cosβ)2+
(r3sinα-r2sinβ)2]1/2,
式中:Br为永磁体剩余磁通密度;r23,r24,r13为磁荷微元P与磁荷微元Q的相对位置长度;σ1,σ2为磁荷的面密度;μ0为真空磁导率。
轴承径向磁力为
(4)
2 四重积分数值求解方法
积分数值求解是先将被积函数和积分微元离散化,再求和。(1)~(3)式均含有r23,r24,r13和r2r3dr2dr3dαdβ等变量,因此只需将上述变量进行离散。将定子、转子的单边径向方向分别分成n1,n2份,则
(5)
(6)
将转子圆环分成C2份,将定子半圆环分成C1份,则
(7)
将(5)~(7)式代入(1)~(3)式可得

(8)

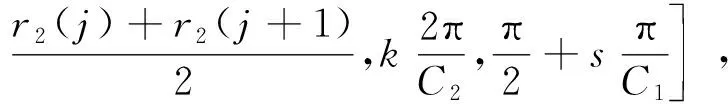
3 高维数值积分的Monte Carlo法
考虑如下形式的n重积分
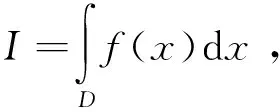
(9)
式中:x=(x1,x2,…,xn)为n维空间中的点;D为n维积分区域。Monte Carlo法计算积分的步骤如下:
1)在D上构造分布密度函数。取D上任一概率密度函数ρ(x),满足条件ρ(x)≠0,当x∈D,f(x)≠0时,令该分布密度函数为

则(9)式可改写为

(10)
(10)式表示I是随机变量F(x)的期望。
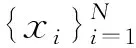
(11)
为便于计算,概率密度函数ρ(x)通常选取D上的均匀分布,即
式中:VD为D的体积。此时
(12)
将(12)式应用到轴承磁力计算所涉及到的四重积分中,有
(13)
式中:ai,bi分别为积分下限和上限。
4 堆叠型永磁轴承模块化计算法
4种典型的被动永磁轴承结构如图2所示。其中,斥力型径向轴承径向刚度为正,轴向刚度为负;吸力型轴向轴承径向刚度为正,轴向刚度为负[10]。前2种轴承结构采用轴向充磁;后2种轴承采用径向充磁。堆叠型永磁轴承可以视为由这4种基本模块组合而成,由于磁力是矢量,满足线性叠加原理,因此堆叠型轴承的磁力是各模块轴承磁力之和。
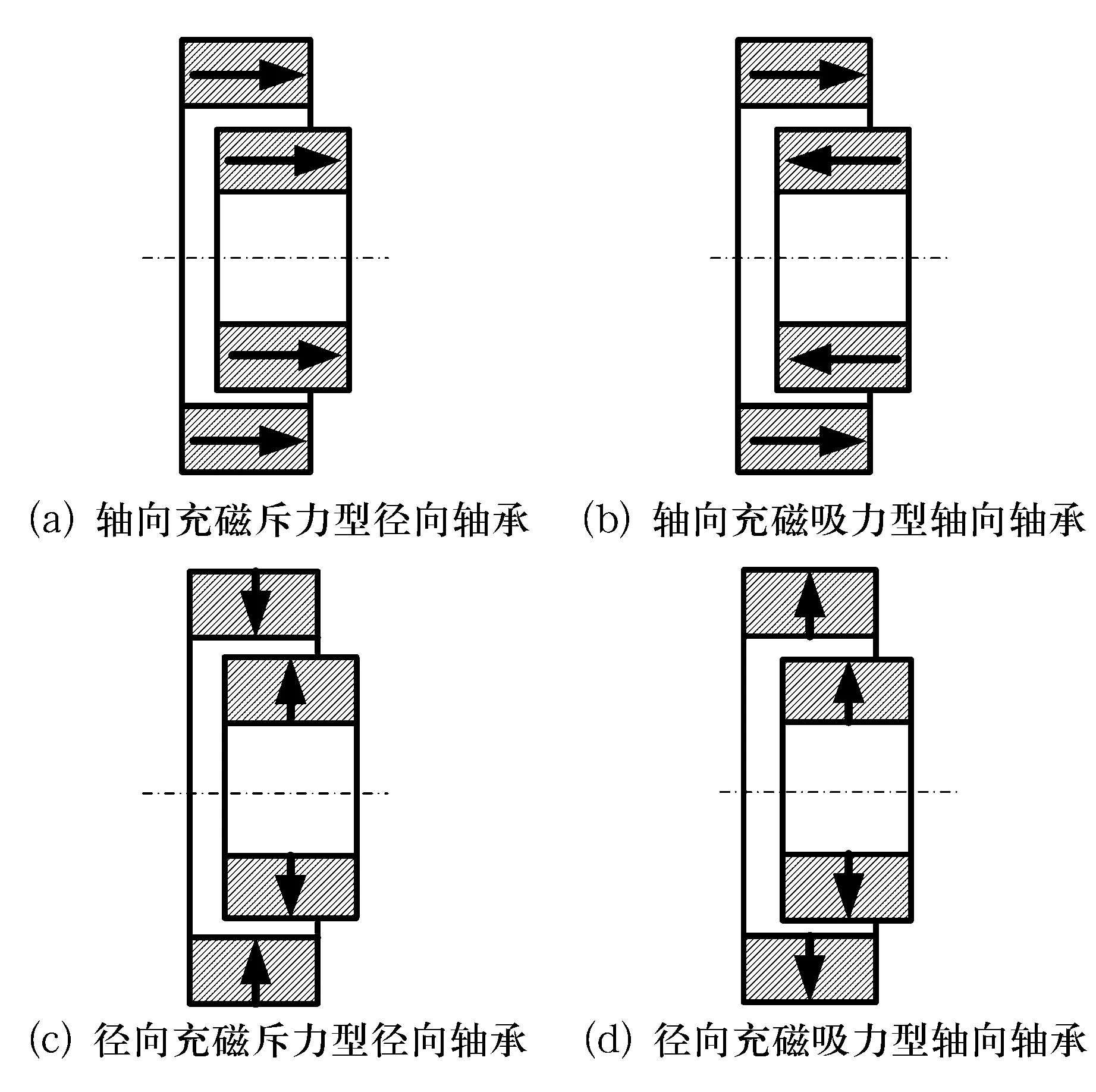
图2 4种常见永磁轴承结构
5 算例分析
考虑定子环为全环和半环的2种情形,其中全环模型尺寸参考文献[7]446,2种模型的主要参数见表1。
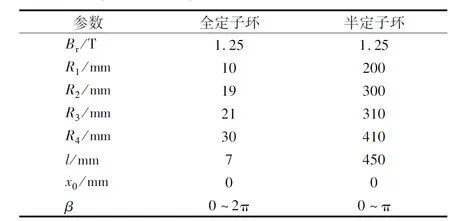
表1 轴向充磁径向永磁轴承主要参数
5.1 for循环计算结果分析
使用for循环方法进行高维数值积分计算,剖分参数见表2。对于本算例,当C1=C2=120,n1=n2=14时,全定子环模型竖直方向磁力Fy的计算结果如图3所示。由图可知,计算结果与文献[7]的结果非常吻合,证明了此方法的正确性。C1,C2,n1,n2取值越大,计算结果越精确,但结果之间的差别非常小。
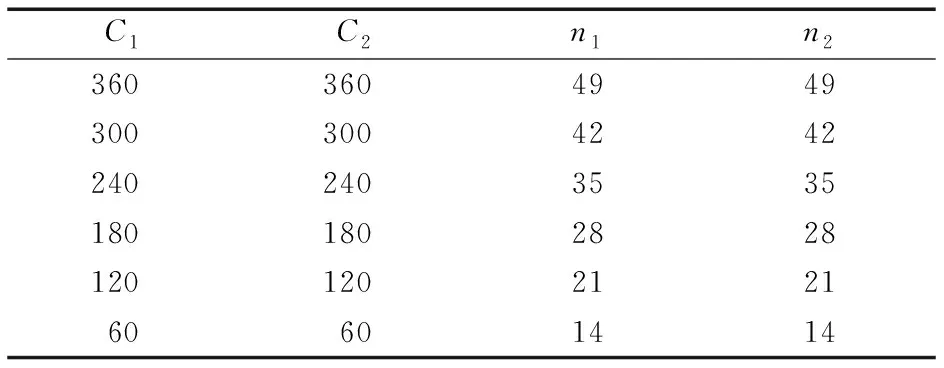
表2 for循环方法进行计算的剖分参数
对于半定子环模型,竖直方向偏心距e=3 mm时,计算结果如图4所示。由图可知,当剖分单元数目小于(28×180)2时,剖分单元数对轴承径向磁力影响显著,且随着剖分数目的增加,轴承径向磁力逐渐增大;当剖分单元数目大于(28×180)2时,轴承径向磁力虽仍随剖分数目的增加而增大,但增幅变小,轴承径向磁力趋于稳定。另外,剖分单元数的增加直接影响程序运行效率,当剖分单元数大于(28×180)2时,剖分单元数对轴承径向磁力的影响不显著,但程序运行耗时t(由MATLAB软件自动记录)随单元数的增加而急剧增长。由此可见,应选择合适的剖分单元数来提高计算效率。
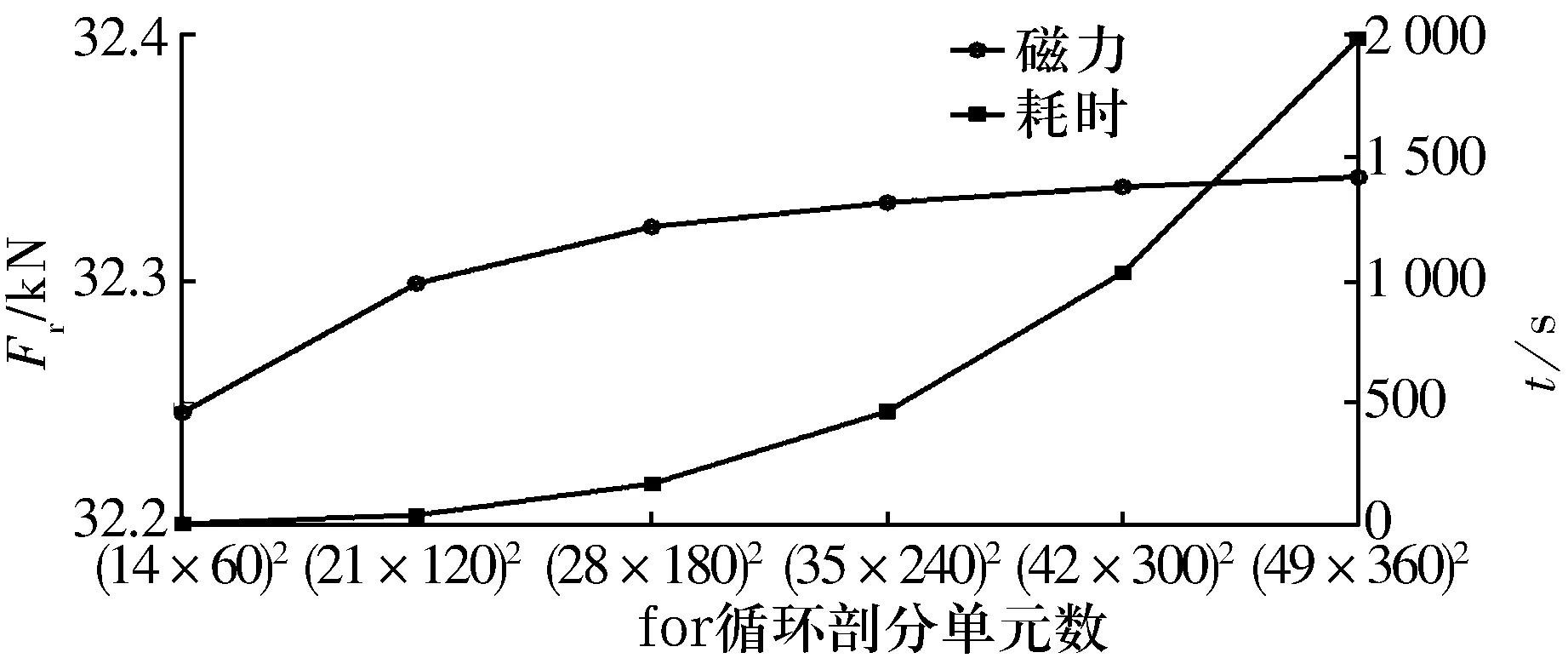
图4 e=3 mm处for循环计算结果
5.2 Monte Carlo计算结果分析
Monte Carlo法是一种近似方法,在使用过程中涉及随机变量的产生,且对于不同随机变量个数N,其计算的积分值一般不同。为确保Monte Carlo法的效果,降低偶然性的干扰,在不同随机变量个数N(1.0×106,5.0×106,1.0×107)下分别运行7次,然后取均值,获得永磁轴承磁力。当e=3 mm时,半定子环模型的计算结果如图5所示。

图5 e=3 mm处Monte Carlo法计算结果
由图5a可知,N越大,轴承径向磁力值波动幅度越小,且轴承径向磁力均值随N的增大而增加。由图5b可知,程序耗时随N的增大而增加,当N分别取1.0×106,1.0×107时,单次Monte Carlo法所需时间分别约为6,60 s。
不同样本数下,轴承径向磁力的均值随偏心距的变化曲线如图6所示。由图可知,轴承径向磁力随偏心距的增加而增大,不同样本数下的曲线非常接近。说明当样本数量达到一定值后(如N=1.0×106),再增加样本数不会导致计算精度发生大幅度变化,因此应当选择合适的样本数来提高计算效率。
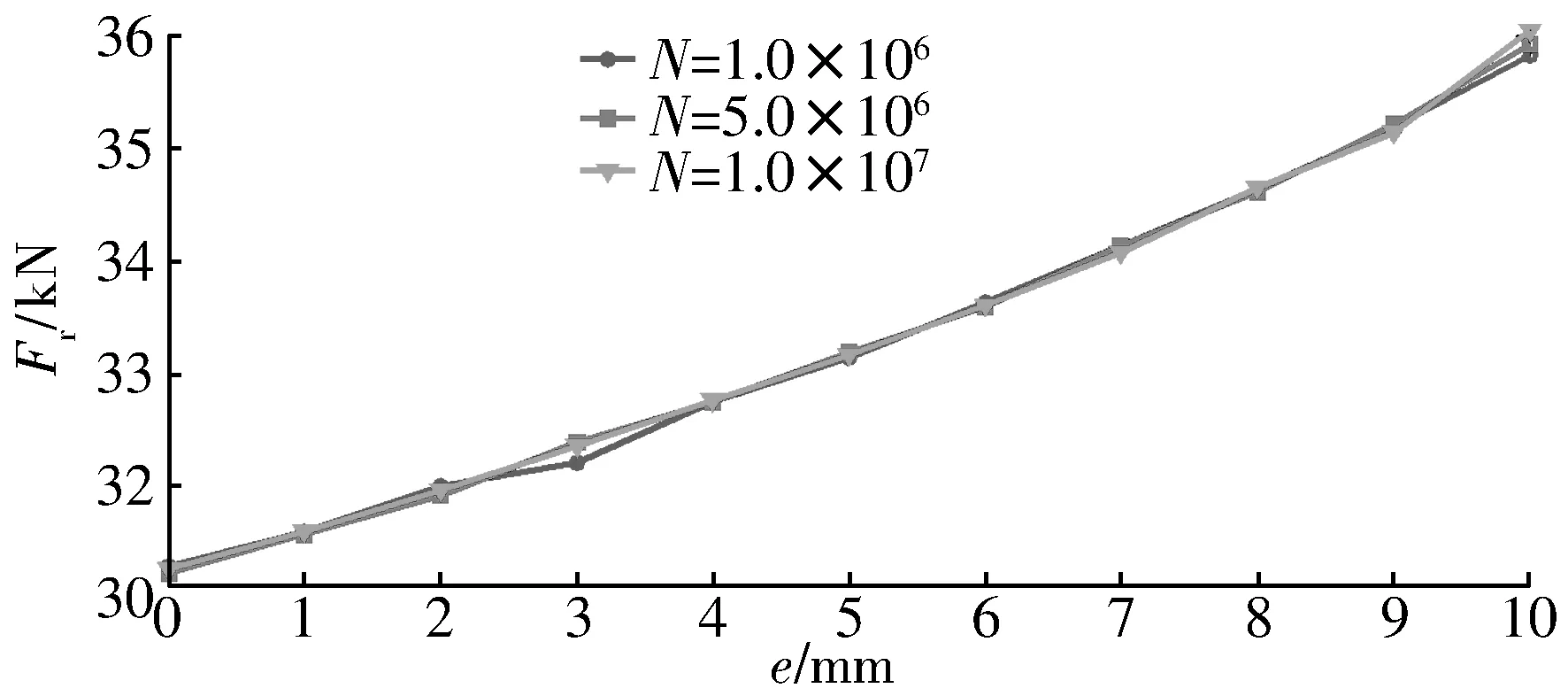
图6 偏心距对轴承径向磁力的影响
5.3 for循环方法和Monte Carlo法的比较
e=3 mm处,通过Monte Carlo法计算不同随机变量个数下运行多次的平均磁力分别为32.20,32.36,32.40 kN,与for循环法计算的磁力(图4)比较可知,2种方法的计算结果吻合良好,随着样本数的增大,Monte Carlo法计算结果越来越逼近for循环方法的极限值。由图4可知,剖分单元数为(28×180)2时,for循环的计算精度可满足要求,但其运行耗时在170 s左右,不仅远高于图5b中N=1.0×106的Monte Carlo法所需时间,甚至是N=1.0×107的Monte Carlo法所需时间的2.5倍,因此,与Monte Carlo法相比,for循环精度的提升需要耗费更多的时间。对于本算例,当N=5.0×106时,Monte Carlo法计算结果与for循环计算结果相差在0.185%之内,但其耗时是后者的10%,说明Monte Carlo法具有更高的计算效率。
需要指出的是,采用四重for循环计算时,为了获得更精确结果,需要将网格划分更密,从而使得计算时间呈几何级数增长;而Monte Carlo法采用打点法,当样本点数增大时,计算时间呈线性增大,这使得Monte Carlo法在初次试探计算时具有更大的时间优势。另外,选择的样本点数N=5.0×106可以作为其他模型初次计算的参考,并不具有普适性,但样本点数的选择应以多次单次计算结果不出现大幅波动为宜。
5.4 堆叠型永磁轴承磁力计算
某堆叠型径向永磁轴承如图7所示,其中R1=12 mm,R2=23.5 mm,R3=29.5 mm,R4=41 mm;定转子永磁环的厚度、宽度均相等,分别为d=11.5 mm,λ=2d;最大偏心距e=2 mm。定子环编号分别为A~D,转子环编号分别为a~d。以转子环a为例,aA和aC组成图2a所示径向轴承(基本模块),aB和aD组成图2b所示的轴向轴承(基本模块),其他定转子环的组合与此类似,所有组合情况见表3。根据模块理论,轴承磁力为表3中所有模块轴承磁力之和。实际上,只需计算4种组合的磁力,即aA,aB,aC,aD,根据结构的对称性,其他组合都属于以上4种情形之一。这4种组合的磁力可以通过Monte Carlo法快速计算出来。

图7 堆叠型径向永磁轴承
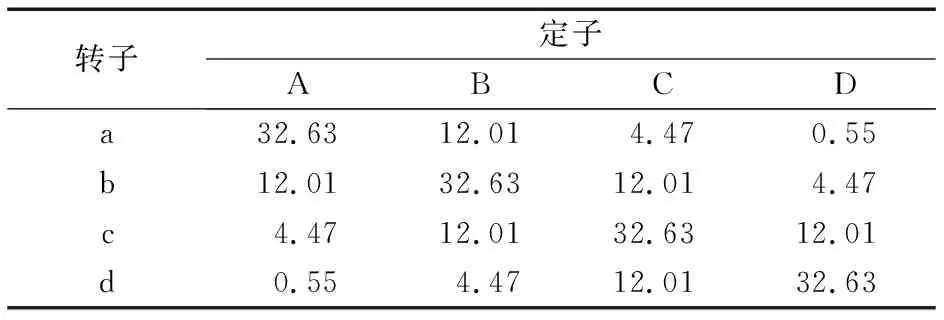
表3 模块轴承匹配表及磁力值
根据表3,图7中轴承最大径向磁力Fymax=32.63×4+12.01×6+4.47×4+0.55×2=221 N。根据文献[15]737中的图表数据估算图7所示的轴承最大径向磁力为207.2 N,两者相对误差仅6.2%,证明了所提出方法的正确性。
6 结论
1)将被动永磁轴承磁力的四重积分离散化,利用MATLAB软件中的四重for循环进行求和运算,求解结果与Monte Carlo法计算结果吻合。
2)与Monte Carlo法相比,for循环精度的提升需要耗费更多的时间。对于文中算例,当N=5.0×106时,Monte Carlo法计算结果与for循环计算结果(稳定值)相差在0.185%之内,但Monte Carlo法具有更高的计算效率。
3)根据叠加原理,将堆叠型轴承的磁力等效为各组合模块轴承磁力之和,通过算例验证了所提方法的正确性,给出了一种适用于工程用的堆叠型轴承磁力的计算方法。
