基于加热光纤分布式温度传感器的土壤含水率测定方法

2019-07-23任姮烨司炳成

农业工程学报 2019年10期

胡优，李敏，任姮烨，司炳成,2

胡优1，李敏1，任姮烨1，司炳成1,2※

（1.西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100； 2.萨斯喀彻温大学土壤科学系，加拿大萨斯卡通市 S7N5A8）

为探讨加热光纤分布式温度传感技术测量土壤含水率不同方法的可行性，通过室内土槽试验，加热埋设于砂土的碳纤维光纤，利用分布式温度传感器测量不同含水率下沿光纤的温度变化，建立最大升温值、累积升温值和热导率与土壤含水率的关系，并比较这3种方法推求土壤含水率的测量精度。结果表明，光纤的温度波动随采样间距的增大或时间间隔的增大均减小，合理的采样间距和时间间隔设置能控制温度波动小于±0.1 ℃。在低（0～0.1 m3/m3）、中（>0.1～0.2 m3/m3）和高（>0.2～0.35 m3/m3）3个含水率水平，热导率法的测量精度均高于最大升温值法和累积升温值法，并且3种方法的测量精度均随含水率增加而降低；热导率法的均方根误差为0.015 m3/m3，低于最大升温值法（0.038 m3/m3）和累积升温值法（0.050 m3/m3）。研究对高时空分辨率精确获取田间尺度土壤墒情信息发展精准农业具有重要意义。

土壤；含水率；热导率；光纤；碳纤维；分布式温度传感器

0 引言

土壤含水率是农业、水文、气象等学科重要的基本参数，实现土壤含水率在田间尺度下实时和连续的分布式原位测定是实施高效农业和精准灌溉的基础。现有土壤含水率的测定主要利用烘干法[1]、时域反射仪（time-domain reflectometry，TDR）法[2-4]、频域反射仪法[5]、中子仪法[6]和热脉冲法[7-9]等进行单个土样或者单点的小尺度测定，或利用卫星遥感法估算千米级大尺度的区域含水率。而在农业生产中最亟需的田间（米到千米级）中尺度却无有效和精确的方法。宇宙射线法可以测量几十厘米深度中尺度的平均含水率[10]，但田间水分的空间变异情况无法获知[11-12]。快速发展的无人机遥感法能根据光谱图像推算田间尺度土壤含水率，但转换关系的不确定性及受天气影响较大限制了测量精度和使用条件[13]，在植被覆盖度高的地方测量困难，且只适用于监测表层土壤的含水率[14]。近年来，分布式温度传感（distributed temperature sensing，DTS）技术开始被应用于土壤含水率的测量[15-16]，有望实现田间尺度下土壤含水率实时、精确、连续的动态原位测定。该方法的另一优点是有望同时得到相同时间、相同地点和相同尺度下的土壤水热信息，为农田、土壤和生态等系统的水热运动、耦合和能量平衡等研究提供基础。

探针热脉冲法是目前测定土壤热性质最流行的方法[17-18]，曾被应用于探测火星土壤热特性，该方法还可以通过热特性与含水率的关系反推求含水率[19]。其中，双探针热脉冲法可以由土壤热容与含水率的线性物理关系推求含水率，但探针间距的变化会给测量带来误差。单探针热脉冲法可以通过热导率与含水率的半理论或经验模型推求含水率[20]。目前，DTS技术测量土壤含水率有被动加热光纤法[16]和主动加热光纤法[21-22]2类。被动加热光纤法通过光纤测量由昼夜辐射引起的近地表温度波动推算含水率，当太阳辐射较弱时（如阴天或受植被遮盖的土地）存在较大的不确定性，只适用于温度波动足够大、深度小于30 cm的地表附近。而基于热脉冲探针原理的主动加热光纤法[23]，可以进行任意时间任意土壤深度的测量，应用更为广泛。其中基于双探针热脉冲的主动加热DTS技术能同时测量土壤热导率、热扩散率和热容，并利用热容推求含水率[24]，但精度易受光纤间距的影响[25-26]，且长距离保持2条布设的光纤相互平行施工难度大，导致其应用受限。单探针热脉冲的主动加热DTS法仅需埋设1条光纤，避免了上述缺点，得到了更多的青睐。该方法可以直接利用热脉冲温度随时间变化的信息，如最大升温值（Δmax）[27]、累积升温值（Δcum）[15]与土壤含水率的经验关系来推求含水率；Ciocca等[28]通过温度信息得到的中间变量热导率（）来推求含水率，但他们加热时间较短，只能通过冷却阶段温度值计算热导率，会增大测量误差。Li等[7]利用热脉冲单探针技术测量土壤含水率，比较了Δmax法、Δcum法和法的优缺点和测量精度。由于不锈钢探针传热性能好，且与土壤颗粒直接接触，而光纤和碳纤维与土壤颗粒间被光纤的多层包裹层隔开，会影响含水率的测量精度。目前，缺乏光纤测量土壤含水率方法的探索和讨论。此外，每一时刻传感光纤上所获得的信息实际上是光纤上某段距离、某段时间内光信号的累加，采样时空分辨率越高，光信号越难区分开，也更易受外界噪音的干扰，因此，需要分析不同时空分辨率对DTS温度测量的影响。

本文利用碳纤维作为加热材料，分析了DTS在不同采样间距、不同时间间隔下温度的波动规律，为满足不同温度精度要求，选择合理的采样间距和时间间隔提供参考；同时，测定了砂土从干燥到饱和不同含水率条件下的热导率和光纤温度变化规律，对比了Δmax法、Δcum法和法测量土壤含水率的精度，为基于单探针热脉冲原理的主动加热光纤-DTS法测量土壤含水率提供依据。

1 基于DTS测定土壤含水率方法

1.1 基于DTS测定土壤含水率的原理

基于DTS测定的热特性结果与设定含水率，建立单调函数关系，然后根据建立的函数关系推求土壤含水率。

DTS是一种基于拉曼散射效应测量温度并通过光的时域反射技术来定位的温度传感器，其测温原理是：一定能量的脉冲泵浦光注入光纤后，光子与光纤分子发生非弹性碰撞，吸收或发出1个声子，产生2束背向拉曼散射光。其中，波长大于入射光的斯托克斯散射光不受温度影响，而波长小于入射光的反斯托克斯散射光有很强的温度依赖性。因此，可以根据斯托克斯与反斯托克斯的光强比计算温度[29]。光纤上任意一点的温度值可表示为[30]

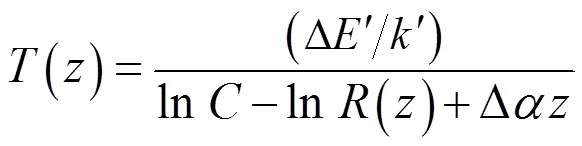
式中为绝对温度，K；(z)为斯托克斯与反斯托克斯的光强比；Δ¢表示驱动拉曼散射的分子能态的差值，J；¢为玻尔兹曼常数，J/K；Δ为斯托克斯与反斯托克斯背向散射光损失系数之差；为到DTS光源的距离，m；为可校准参数，它与入射光的波长、频率、背向拉曼散射光、仪器的光子探测器有关。

光纤上任一点的位置，即为光行走路程的一半。

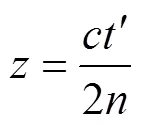
式中是光在真空中的速度，m/s；是光纤包层的折射率；´为光向前与向后传播所需要的时间，s。

1.2 基于3种热脉冲特性的含水率估算方法

1.2.1 最大升温值法

由于加热阶段早期的温度数据受光纤热特性和接触热阻影响较大，Striegl[27]把温度上升达到稳定阶段（温度值与时间的对数为线性关系）的平均值作为最大升温值Δmax。Δmax计算公式为

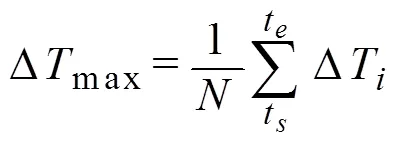
式中t为上述稳定阶段的起始时间，根据先验试验结果，本文t取为390 s；t为停止加热的时间，本文为600 s；ΔT为第个时刻的升温值，由加热后该时刻的温度值减去初始温度值（加热前5 min温度的平均值）求得；为稳定阶段内升温值的数量。当加热条件一定时，max随着土壤含水率增大而减小。利用测定的max与含水率的单调函数关系能推求土壤含水率。

1.2.2 累积升温值法

Sayde等[15]提出光纤被加热后，土壤含水率越低则累积升温值Δcum越大，根据这个规律，Δcum可以用来推求含水率。Δcum计算公式为

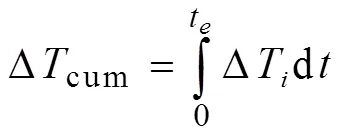
对温度进行积分包含了一定含水率条件下整个加热过程的温度变化，光纤温度的变化取决于土壤含水率，因此根据Δcum与含水率的标定关系可以推求含水率。

1.2.3 热导率法—瞬时单探针热脉冲理论

把光纤看成是一个无限长的线性热源。对于一个无限的恒定热量输入的线性热源，环境温度不变化，在无限大的均匀介质中径向的热传导方程可以表示为[17, 31]

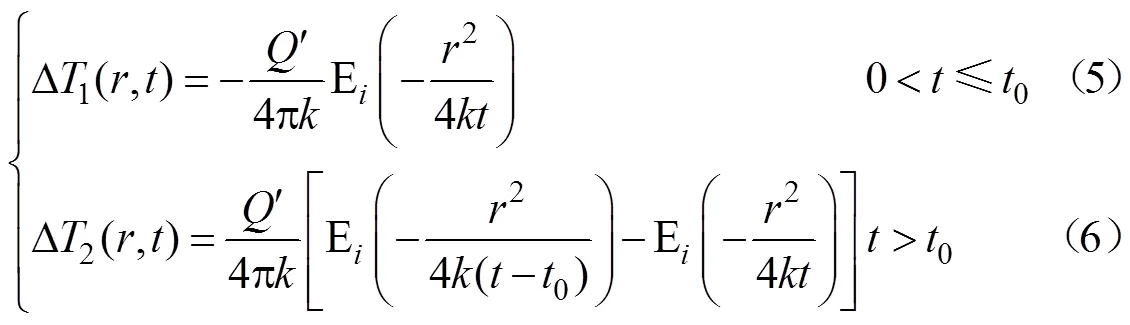
式中Δ1和Δ2分别是加热和冷却阶段温度的增量，℃；-E（-）是指数积分函数；0是热源加热时间，s；是某个时刻，s；是温度感应器到热源的某个距离，m；是热扩散率，m2/s；¢=¢/ρ为单位时间的热强度，（m2·℃）/s；'是单位时间单位长度输入的热量，J/(m·s)；ρ是介质的体积热容量，J/(m3·℃)。

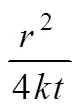
式中λ和λ分别为加热、冷却阶段的热导率，W/(m·℃)，则热导率=¢/(4π)，为方程（7）或（8）的斜率；和'为常数，与时间无关。因为加热阶段计算的热导率比冷却阶段更加准确[33]，本文采用加热阶段的升温值计算土壤热导率。

土壤热导率是含水率的单调递增函数，通过建立与的关系从而推求。

2 材料与方法

2.1 供试材料

本试验在西北农林科技大学水利与建筑学院水热测定实验室进行，利用热脉冲DTS技术测量砂土的含水率，室内试验从2017年10月2日开始到2018年4月6日结束。试验材料砂土取自陕西杨凌渭河河岸，砂土容重为1.53 g/cm3，饱和含水率为0.33 m3/m3，pH值为8.5。在室内烘干并过1 mm筛，分3次压实装入长宽高为4.0 m × 0.3 m × 0.3 m的不锈钢槽。光纤室内水分现场测试如图1。

图1 光纤土壤水分室内测试照片

2.2 试验设计及过程

2.2.1 DTS温度精度分析试验

分析不同采样间距、不同时间间隔条件下DTS温度的波动规律，以评估DTS系统本身测定温度的精度，并确定合适的采样间距。光纤总长40 m，将首尾两端各10 m置于冰浴保温箱中，在冰浴箱底部放置起泡器，使冰水混合均匀并防止温度上下结层、分布不均。分别设置6个采样时间间隔1、2、4、10、20和30 s，4个采样间距0.125、0.25、0.50和1.00 m，共24个组合，每个组合重复测量3次，每次测量10 min，在冰浴内共进行了72次温度测试。

2.2.2 DTS测量土壤含水率试验

将光纤埋设于装有砂土的土槽，对光纤的碳纤维包裹层加热，利用DTS记录不同含水率下光纤的温度随时间变化特征，并通过上述3种方法推求土壤含水率。试验布置如图2所示。分布式温度传感器为英国Silixa公司生产的ULTIMA-S，其最小采样距离为0.125 m，最大采样间距为1.0 m，空间分辨率为0.25 m，时间分辨率为1 s，温度分辨率为0.01 ℃，感测距离长达5 km。设置DTS采样时间间隔为30 s，空间间距为0.5 m。为了使光纤加热过程能够受热均匀并且产生足够的热量，采用苏州南智传感科技有限公司生产的碳纤维内加热型光纤NZS-DTS-C09，该光纤耐电电压为0~360 V，电阻为21 Ω/m，外径8.3 mm，工作温度为-20~120 ℃。光纤由内到外依次为纤芯、包层、涂覆层和光纤护套、碳纤维、纤维护套，如图2所示。采用TDR-315连续测定试验期间的土壤含水率并通过数据采集器（CR1000，Campbell Scientific）连续采集含水率数据。PT100为铂电阻温度传感器，与光纤一同置于冰浴箱中，作为DTS测量的参考温度。光纤首尾两端各10 m置于冰浴保温箱内用以校准DTS测得的温度，直至光纤温度接近PT100的温度开始进行试验测量。

碳纤维光纤布置在土槽中心，用DTS测量加热和冷却阶段（停止加热后的10 min时长）的温度值。DTS仪器测量并记录图2中到DTS仪器的距离分别为17.76、18.26、18.76、19.26、19.76、20.26、20.76和21.26 m 的光纤上8个位置的温度值，间距为0.5 m（和DTS采样间距一致），再通过显示器实现实时监测；将电线连接碳纤维光纤与可调变压器，用来给光纤加热，加热功率为5.77 W/m，每次加热时间10 min，每日重复3次。在土槽中布设8个TDR，与光纤上8个温度测点对齐，对含水率进行连续测定。先进行了干砂土试验，然后在土槽土壤表层铺1层滤纸，往槽中加水，直至表面有积水，让其充分饱和，进行饱和砂土试验。之后，将土槽底部预留的排水孔打开，确保底部无积水，用空调保持室内恒温，让土壤自由蒸发，这样可以使土壤水分分布均匀，直至接近干砂土，期间进行不同含水率的非饱和砂土试验。

试验测试顺序为从干砂土到饱和砂土最后到非饱和砂土，避免了重新装填或配不同含水率的土壤造成对土壤结构的扰动。每次加热后DTS测量8个测点的温度值，每天加热并测量3次，取3次测量的温度平均值作为该日光纤加热后温度的变化，并用其计算热导率。同时，用TDR监测土壤含水率，1 d中土壤含水率变化量忽略不计。由于17.76和21.26 m位置的光纤处于土槽边界受边界效应影响，而18.26和20.76 m位置排水过快使含水率值的分布范围过窄，所以，以上4个位置的测试结果后文不进行分析。本文通过加热光纤的方法，用DTS记录了整个含水率范围加热后温度的动态变化，然后计算得到Δmax、Δcum和。用TDR连续监测土壤含水率。总共测量的样本数量为22组，采用其中12组Δmax、Δcum和对应的含水率数据拟合得到标定曲线，另外10组数据验证标定曲线推求含水率的准确性，验证数据包含了高、中、低3个含水率水平。

注：DTS为分布式分布传感器；图中TDR对应的数值为光纤上的点到DTS的距离，m。

2.3 测量精度评价指标

烘干法是校正其他土壤含水率测定方法的唯一标准方法，但该方法需要在试验过程中不断取土，对土槽土样具有破坏性，因此，本研究利用基于时域反射技术的TDR-315（Acclima，美国）探针原位监测测定的土壤含水率来验证DTS法测得的含水率，并采用均方根误差（root mean square error，RMSE）和决定系数22个指标进行评价。试验前已利用烘干法对TDR-315测量误差进行校正。

3 结果与分析

3.1 采样间距确定

尽管本研究使用的DTS采样间距和时间间隔较大，但越高的时空采样频率下温度值的精度可能会受影响，因此，确定适宜的采样间距是DTS获取准确温度不可或缺的一步。考虑到冰浴内温度在测量时间内可以保持相对稳定，观察冰浴内光纤恒定温度下的波动情况能反映仪器的系统误差。表1是不同采样间距Δ、时间间隔Δ的温度波动（为冰浴中光纤上距离DTS仪器10 m位置20 min内温度的标准差）。可以看出温度波动随着Δ和Δ的增大而减小。当（Δ，Δ）为（0.125 m，1 s）时温度波动最大，达到±0.71 ℃；（Δ，Δ）为（1 m，30 s）时温度波动最小为±0.07 ℃，这2种组合温度波动相差约10倍。（Δ，Δ）为（0.5 m，10 s）、（1 m，4 s）和（1 m，10 s）或Δ>20 s时，光纤的温度波动都小于0.2 ℃，可满足大多数应用需求。实际使用中可根据表1规律及研究和应用需求确定适宜的采样间距和时间间隔。因为本试验采用的是4 m长土槽，为了得到足够的温度采样点，并且让温度波动控制在0.1 ℃范围内，因此本文选择的（Δ，Δ）为（30 s，0.5 m）。

表1 不同采样间距及时间间隔下DTS的温度波动

3.2 基于3种方法的土壤含水率估算结果

图3是不同含水率条件下砂土加热和冷却过程中土壤升温值（Δ，由加热后的光纤温度值减去加热前5 min的温度平均值求得）的动态变化。从图3可以看出，Δ随土壤含水率增大而减小，从0～600 s（600 s停止加热），干砂土的Δ最大为10.85 ℃，饱和砂土的Δ最小为4.49 ℃。加热过程中，Δ的上升速率逐渐减小，并逐渐趋于稳定；Δ的增加速率随含水率的增加而减小（图3），这是因为土壤颗粒间存在“水桥”的连接，使得含水率更高的土壤具有更好的导热路径，并且具有更大的热容量。体积含水率在0.24～0.33 m3/m3时，升温曲线几乎重叠，说明该区间的含水率不再是影响土壤传热的决定因素，也进一步说明随着含水率增大，Δ对含水率的敏感性逐渐降低。

图3 不同含水率下DTS测定的土壤升温值动态变化

用最小二乘法拟合了Δmax、Δcum及与含水率在光纤不同位置的标定曲线（如图4），2都很高，均在0.96以上（表2），拟合度良好。Δmax与Δcum随含水率的变化有相似的变化趋势，与含水率呈指数递减关系，并且随含水率增大曲线斜率逐渐减小，说明Δmax与Δcum对含水率的敏感性逐渐降低，这些与Sayde等[15]和Striegl等[27]研究结果契合。与含水率呈指数递增关系，随含水率的增大曲线斜率没有明显减小的趋势，说明在砂土的整个含水率范围，热导率对含水率都有较好的敏感性，与Ciocca等[28]研究结果一致。随着含水率越大，3种方法的观测值（图4中实心点，拟合得到标定曲线）偏离标定曲线越远，这是因为土壤水中，只有吸湿水、薄膜水和毛管水能够传递热量给土壤颗粒，而自由水（重力水）做无规则布朗运动，一定程度上会阻碍热量的传递。对于不同的土壤质地、容重、有机质含量等，标定曲线会有差异，所以要对它们分别校正。

对表2中公式进行验证，通过求预测值（DTS测得的最大升温值、累积升温值和热导率通过3种方法得到的标定曲线推求的含水率）与实测值（TDR-315观测的含水率）之间的RMSE，来比较3种方法在不同含水率范围的误差程度（如图5和表3）。对于法，在整个含水率范围，测量值与预测值的散点均在或者靠近1∶1线，有良好的预测结果。对于Δmax和Δcum法，含水率为0～0.1 m3/m3范围，散点都在1∶1线的周围，有较好的预测结果，0.1～0.25 m3/m3的范围，散点都在1∶1线的下方，会低估含水率，而大于0.25 m3/m3的范围，散点大都在1∶1 线的上方，会高估含水率。

划分了3个含水率范围（低、中、高）比较3种方法预测值与实测值的RMSE，结果表明，低的含水率范围RMSE小，高的含水率范围RMSE大（如表3），这是因为随着含水率的增大，Δcum、Δmax、对含水率的敏感性逐渐降低。在0～0.1 m3/m3的含水率范围，3种方法的RMSE差异不大，Δcum法比Δmax法略高0.007 m3/m3，Δmax法比法略高0.008 m3/m3。在0.1～0.2 m3/m3的含水率范围，Δcum法与Δmax法差异很小，但都比法高0.03 m3/m3。在0.2～0.35 m3/m3的含水率范围，3种方法之间差异都较大，Δcum法比Δmax法高0.025 m3/ m3，Δmax法比法高0.03 m3/m3。对每个含水率范围，RMSE的大小顺序为Δcum>Δmax>法，法在整个含水率范围都具有较好的准确度，法预测含水率效果要优于其他2种方法。

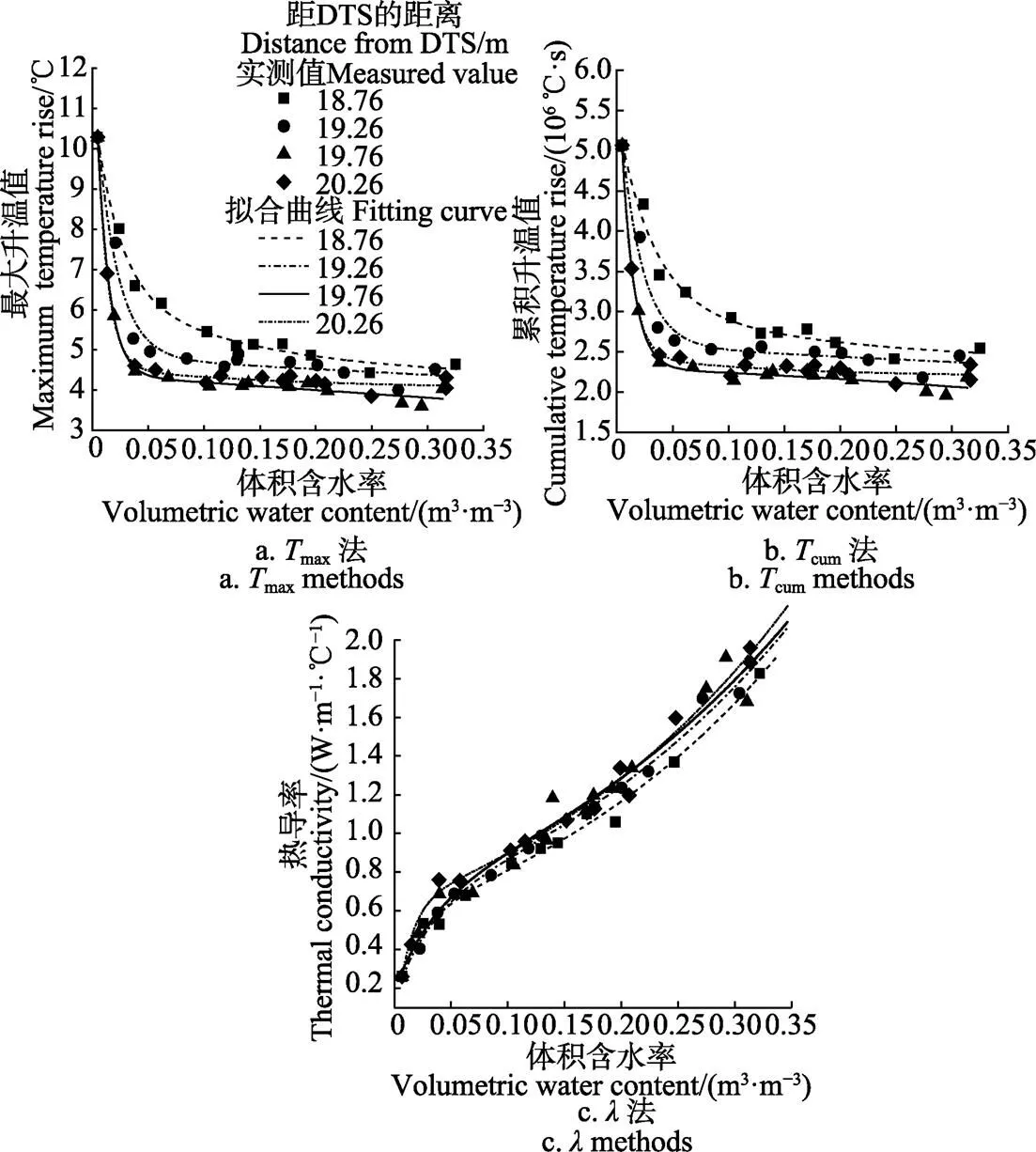
注：各处理样本数为12。

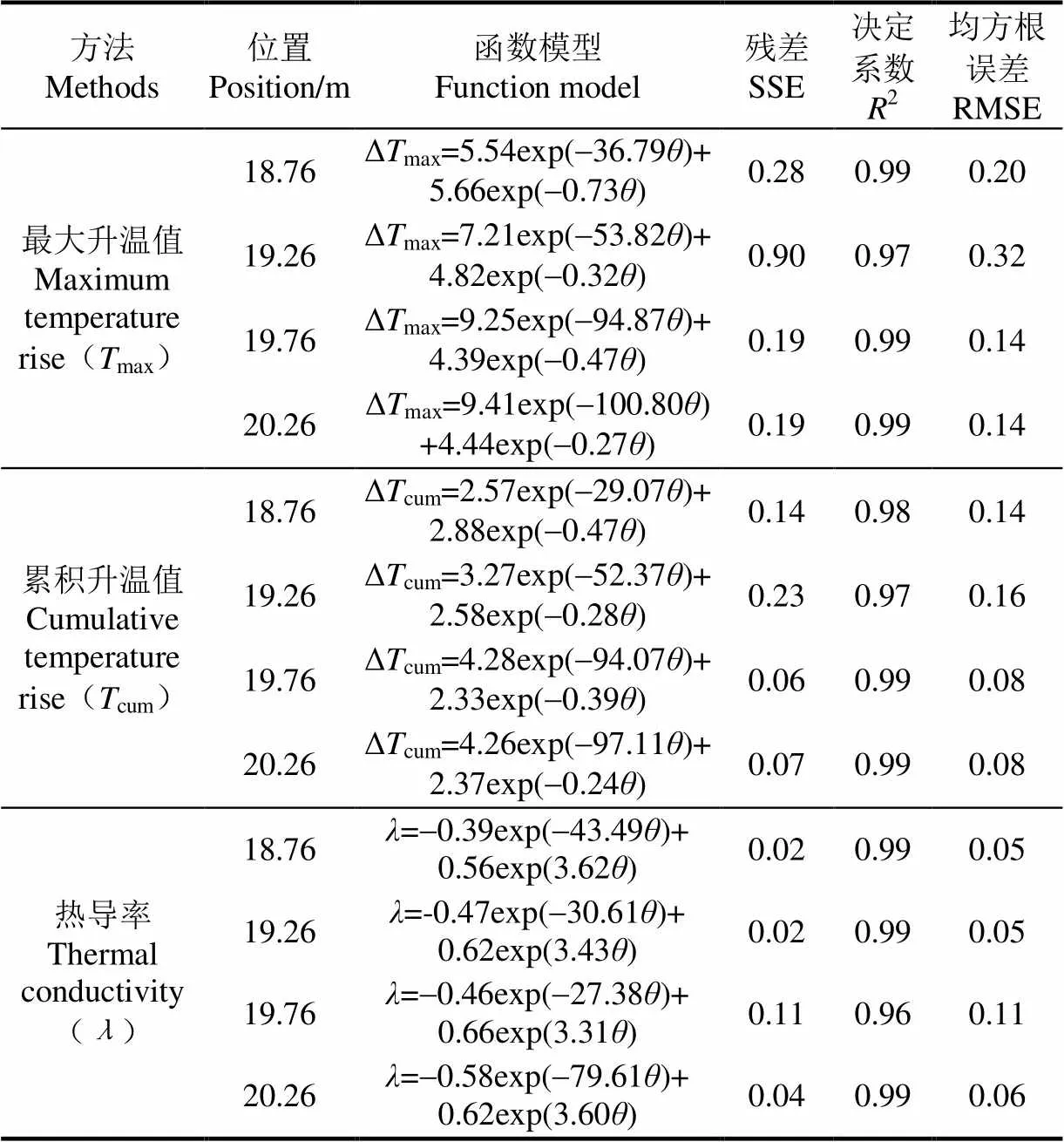
表2 3种方法得到的光纤上不同位置的标定曲线及拟合效果

注：Δmax、Δcum和分别为最大升温值（℃）、累积升温值（℃）和热导率（W·m-1·℃-1）。下同。

Note: Δmax、Δcumandare the maximum temperature rise (℃), cumulative temperature rise (℃) and thermal conductivity (W·m-1·℃-1), respectively.Same as below.

注：各处理样本数为10。

表3 3种方法在不同含水率范围的均方根误差（RMSE）

3 讨论

3.1 有关研究精度的比较

本文对高中低3个含水率范围3种方法的DTS测量精度进行了分析。Sayde等[15]通过室内土柱试验首次采用Δcum法测量砂土含水率，研究表明，Δcum法的测量误差随含水率的增加呈线性关系，体积含水率为0.05 m3/ m3时，测量的可重复性精度为0.001 m3/m3；体积含水率为0.41 m3/m3时，可重复性精度为0.046 m3/m3。本研究Δcum法3个含水率范围的RMSE在0.027~0.075 m3/m3之间，但整个含水率范围的平均RMSE小于0.05 m3/m3。Striegl等[27]利用Δmax法测量了田间尺度的含水率，体积含水率≤0.31 m3/m3时，RMSE为0.016 m3/m3；体积含水率>0.31 m3/m3时，RMSE达到0.05 m3/m3，本研究的Δmax法3个含水率范围得到的RMSE在0.02～0.05 m3/m3之间，与Striegl等的结果接近。Ciocca等[28]采用法在土柱中测量了壤土含水率，研究表明，含水率为0.3 m3/m3时，测量的精确度为0.04 m3/m3，本文在高含水率范围，法精度也能达到0.02 m3/m3，一方面Ciocca等只加热120 s，加热阶段还达不到升温值的渐近线，采用冷却阶段温度值计算会带来误差[33]；另一方面将光纤盘卷在土柱中，也不符合线性热源的假设，从而影响含水率测量的准确度。所以本研究Δcum和Δmax法的含水率测量精度与其他作者接近，但法测量精度在高中低3个含水率水平都要优于他人研究。

3.2 3种方法的探讨

Sayde等[15]研究表明，Δcum法测量含水率的误差显著小于Δmax法，与本文结果刚好相反，主要因为本文的采样时间间隔是30 s，而Sayde的时间间隔是5 s，所以Sayde能把整个加热时间分割成很微小的片段，提高了计算Δcum的准确度，进而减小含水率测量误差。因此，应用Δcum法预测含水率时，应适当减小采样时间间隔。付永威等[34]和Li等[7]研究表明，的计算受探针特性的影响很小，而Δmax和Δcum会受探针特性的影响[7]，这也是本研究光纤上不同位置处Δmax和Δcum差异较大而差异较小的原因，从而导致了Δmax和Δcum法测量含水率误差较大。并且，当>0.1 m3/m3时Δmax和Δcum法对敏感性变弱，而法依然具有较好的敏感性，因而，法优于Δmax和Δcum法。所以，要提高Δmax和Δcum法的测量精度，还得提高碳纤维光纤的制作工艺，主要提高碳纤维包裹光纤和横纵向分布的均匀度，并适当减小光纤护套厚度。Benítez-Buelga等[35]提到了用主动加热光纤法估算并用其预测含水率，但作者考虑光纤护套的影响没有利用光纤测量，最后通过Δcum法预测了土壤含水率。然而，光纤护套对估算是否真正存在影响，还有待进一步研究。总之，Δmax和Δcum法虽然能够达到一定的精度，但最大升温值和累积升温值没有物理意义，两者与含水率之间为经验关系，受光纤特性、热源能量的输入及土壤物理性质等多种因素影响。但其优点是加热时间比法短，如图3所示，仅需加热不到200 s，不同含水率土壤的升温值已有明显区分度，但热导率的计算需要更长时间的加热才能得到升温渐近线。加热时间短在野外电源受限时优势明显。法具有物理意义，只与土壤物理性质有关，而且与的关系已有许多研究进展，并发展了很多（）模型，这为通过土壤热导率推求含水率提供了简便可行的方法。所以利用法的主动加热光纤-DTS测量具有很重要的现实意义。

3.3 误差来源分析

测量含水率的不确定性主要来自几个方面：1）加热碳纤维采用的是交流电源，日内电压会有一些波动，导致加热功率会有微小偏差。2）TDR-315由于受土壤接触间隙或盐分的影响，测量含水率也存在一定的不确定性。虽然，本研究采用的DTS是当今十分先进的设备，分辨度、精度都很高，但也会受到外界噪音的干扰，因为室内试验，干扰不会很大，所以DTS带来的不确定性很小。本研究采用的碳纤维光纤还未广泛使用，处在测试阶段，光纤的制作工艺、结构需要进一步改善，碳纤维的均匀度可能会带来一定的不确定性。

测量误差可以通过如下3种方式减少[15]：1）通过多次热脉冲结果的平均来提高信噪比；2）增大加热强度；3）延长加热时间。然而，增大加热强度、延长加热时间虽可以提高DTS测量准确度，但也要防止土壤温度升高过大使得光纤周围土壤水分在温度势作用下重新分布，甚至产生相变。

4 结论

本文分析了碳纤维加热光纤-分布式温度传感器不同采样间距和时间间隔对温度波动的影响，对比了最大升温值法、累积升温值法和热导率法测量含水率的精度，结论如下：

1）温度波动随采样间距的增大或时间间隔的增大均减小，本研究使用的DTS的最大时空采样分辨率（1 s，0.125 m）下温度波动最大，范围为±0.71 ℃，采用合理的采样间距和时间间隔设置能控制温度波动小于±0.1 ℃；用户需根据需求选择合理的采样参数以降低温度波动从而减小测量误差；

2）最大升温值、累积升温值和热导率与土壤含水率的关系均可用指数函数表达。3种方法计算的土壤含水率均与实测含水率接近，但最大升温值法和累积升温值法在含水率较高时稍微高估含水率。3种方法的测量精度均随含水率增加而降低。在低含水率（0～0.1 m3/ m3）、中含水率（>0.1～0.2 m3/m3）和高含水率（>0.2～0.35 m3/m3）范围内，热导率法的测量精度均高于最大升温值法和累积升温值法；热导率法的总体精度（RMSE为0.015 m3/m3）高于最大升温值法（RMSE为0.038 m3/m3）和累积升温值法（RMSE为0.050 m3/m3）；因此，3种方法均能较准确测量土壤含水率，且热导率法的测量精度更高。

[1] O¢Kelly B C, Sivakumar V. Water content determinations for peat and other organic soils using the oven－drying method[J]. Drying Technology, 2014, 32(6): 631－643.

[2] Černý R. Time-domain reflectometry method and its application for measuring moisture content in porous materials: A review[J]. Measurement, 2009, 42(3): 329－336.

[3] Evett S R. Soil Water Measurement By Time Domain Reflectometry[M]. New York: Encyclopedia of Water Science, 2003:894－898.

[4] Baker J M, Allmaras R R. System for automating and multiplexing soil moisture measurement by time-domain reflectometry[J]. Soil Scisocamj, 1990, 54(1): 1－6.

[5] Tsheko R, Savage M J. Calibration of a frequency-domain reflectometer for determining soil-water content in a clay loam soil[J]. Water Sa, 2006, 32(1): 37－42.

[6] Evett S R, Steiner J L. Precision of neutron scattering and capacitance type soil water content gauges from field calibration[J]. Soil Scisocamj, 1995, 59(4): 961－968.

[7] Li M, Si B C, Hu W, et al. Single-probe heat pulse method for soil water content determination:Comparison of methods[J]. Vadose Zone Journal, 2016, 15(7): 1－13.

[8] Basinger J M, Kluitenberg G J, Ham J M, et al. Laboratory evaluation of the dual-probe heat-pulse method for measuring soil water content[J]. Vadose Zone Journal, 2003, 2(4): 552－560.

[9] Kamai T, Kluitenberg G J, Hopmans J W. A dual-probe heat-pulse sensor with rigid probes for improved soil water Content Measurement[J]. Soil Science Society of America Journal, 2015, 79(4): 1059－1072.

[10] Bogena H R, Huisman J A, Baatz R, et al. Accuracy of the cosmic-ray soil water content probe in humid forest ecosystems: The worst case scenario[J]. Water Resources Research, 2013, 49(9): 5778-5791.

[11] Rosolem R, Shuttleworth W J, Zreda M, et al. The effect of atmospheric water vapor on neutron count in the cosmic-ray soil moisture observing system[J]. Journal of Hydrometeorology, 2013, 14(5): 1659－1671.

[12] Zreda M, Shuttleworth W J, Zeng X, et al. COSMOS: The cosmic-ray soil moisture observing system[J]. Hydrology and Earth System Sciences, 2012, 17(3): 1065－1076.

[13] Wang L, Qu J J. Satellite remote sensing applications for surface soil moisture monitoring: A review[J]. Frontiers of Earth Science in China, 2009, 3(2): 237－247.

[14] Weihermüller L, Huisman J A, Lambot S, et al. Mapping the spatial variation of soil water content at the field scale with different ground penetrating radar techniques[J]. Journal of Hydrology, 2007, 340(3): 205－216.

[15] Sayde C, Gregory C, Gil-Rodriguez M, et al. Feasibility of soil moisture monitoring with heated fiber optics[J]. Water Resources Research, 2010, 46(6):1－8.

[16] Steele-dunne S C, Rutten M M, Krzeminska D M, et al. Feasibility of soil moisture estimation using passive distributed temperature sensing[J]. Water Resources Research, 2010, 46: 1－12.

[17] Bristow K L. Measurement of thermal properties and water content of unsaturated sandy soil using dual-probe heat-pulse probes[J]. Agricultural & Forest Meteorology, 1998, 89(2): 75－84.

[18] Bristow K L, Kluitenberg G J, Goding C J, et al. A small multi-needle probe for measuring soil thermal properties, water content and electrical conductivity[J]. Computers & Electronics in Agriculture, 2001, 31(3): 265－280.

[19] 张晓, 王月月, 任图生. 利用热脉冲技术测量土壤表层含水率 [J]. 农业工程学报, 2015, 31(2): 72－78. Zhang Xiao, Wang Yueyue, Ren Tusheng. Measuring soil water content in surface layer with heat-pulse technique[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(2): 72－78. (in Chinese with English abstract)

[20] Lu S, Ren T S, Gong Y S, et al. An improved model for predicting soil thermal conductivity from water content at room temperature[J]. Soil Science Society of America Journal, 2007, 71(1): 8－14.

[21] Sayde C, Thomas C K, Wagner J, et al. High-resolution wind speed measurements using actively heated fiber optics [J]. Geophysical Research Letters, 2015, 42(22): 10064－10073.

[22] Sayde C, Buelga J B, Rodriguez-Sinobas L, et al. Mapping variability of soil water content and flux across 1–1000 m scales using the actively heated fiber optic method[J]. Water Resources Research, 2015, 50(9): 7302－7317.

[23] He H, Dyck M, Horton R, et al. Distributed Temperature Sensing for Soil Physical Measurements and Its Similarity to Heat Pulse Method[M]. Cambridge: Academic Press, 2017:173－230.

[24] Benítezbuelga J, Sayde C, Rodríguezsinobas L, et al. Heated fiber optic distributed temperature sensing: a dual－probe heat-pulse approach[J]. Vadose Zone Journal, 2014, 13(11): 1－10.

[25] Kluitenberg G J, Kamai T, Vrugt J A, et al. Effect of probe deflection on dual-probe heat-pulse thermal conductivity measurements[J]. Soil Science Society of America Journal, 2010, 74(5): 1537－1540.

[26] Liu G, Li B, Ren T, et al. Analytical solution of heat pulse method in a parallelepiped sample space with inclined needles[J]. Soil Science Society of America Journal, 2008, 72(5): 1208－1216.

[27] Striegl A M. Heated distributed temperature sensing for field scale soil moisture monitoring[J]. Ground Water, 2012, 50(3): 340－347.

[28] Ciocca F, Lunati I, Van De Giesen N, et al. Heated optical fiber for distributed soil-moisture measurements: A lysimeter experiment[J]. Vadose Zone Journal, 2012, 11(4): 1－11.

[29] Tyler S W, Selker J S, Hausner M B, et al. Environmental temperature sensing using Raman spectra DTS fiber-optic methods[J]. Water Resources Research, 2009, 45:W00D23.doi:10.1029/2008WR007052.

[30] Hausner M B, Suárez F, Glander K E, et al. Calibrating single-ended fiber-optic raman spectra distributed temperature sensing data[J]. Sensors, 2011, 11(11): 10859－10879.

[31] De Vries D A, Peck A J. On the cylindrical probe method of measuring thermal conductivity with special reference to soils. I. Extension of theory and discussion of probe characteristics[J]. Aust J Phys, 1958, 11(62): 65－70.

[32] Blackwell J H. A transient-flow method for determination of thermal constants of insulating materials in bulk part I-theory[J]. Journal of Applied Physics, 1954, 25(2): 137－144.

[33] Dang L, Leong W H. Thermal conductivity probe-part II-an experimental analysis[J]. International Journal of Heat and Mass Transfer, 2015, 86(10): 4－14.

[34] 付永威, 卢奕丽, 任图生. 探针有限特性对热脉冲技术测定土壤热特性的影响[J]. 农业工程学报, 2014, 30(19): 71－77. Fu Yongwei, Lu Yili, Ren Tusheng. Influences of finite probe property on soil thermal property estimated by heat pulse technique[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(19): 71－77. (in Chinese with English abstract)

[35] Benítez-Buelga J, Rodríguez-Sinobas L, Calvo R S, et al. Calibration of soil moisture sensing with subsurface heated fiber optics using numerical simulation[J]. Water Resources Research, 2016, 52(4):2985－2995.

Measurement of soil water content using distributed temperature sensor with heated fiber optics

Hu You1, Li Min1, Ren Hengye1, Si Bingcheng1,2※

(1.712100,2.758,)

Soil water content has great spatial-temporal variability, so accurate field-scale soil water content acquisition with high spatial-temporal resolution is of grave significance for precision agriculture. The distributed temperature sensing (DTS) technology combined with the principle of heat pulse probe is expected to achieve this goal; however, there isn’t research to compare and evaluate the advantages and disadvantages of different methods to estimate soil water content using heated DTS technology. In this study, the indoor soil tank tests were carried on to heat the carbon-fiber optical cable embedded in sand, and the temperature variations along the fiber optics at different water content were measured by the DTS. The relationship between soil water content and maximum temperature rise, cumulative temperature rise and thermal conductivity were established, and the measurement accuracies of soil water content derived from the above mentioned 3 estimated methods were compared. The results showed that the temperature fluctuation of the fiber optics decreased with the increase of the sampling spacing or the time interval, and the reasonable sampling spacing and time interval could control the temperature fluctuation within a range between -0.1 and 0.1 ℃. The temperature rise value of fiber optics decreased with the increase of soil water content. The temperature rise was the highest for the dry sand and was the smallest when the soil was saturated. The maximum temperature rise and cumulative temperature rise had a similar trends with the change of water content, and decreased exponentially with the increase of water content. The slope of curve decreased gradually with the increase of water content, and the sensitivity to water content gradually reduced. However, there was an increased exponential relationship between thermal conductivity and water content. With the increase of water content, the slope of curve did not decrease obviously. In the whole range of water content of sand, thermal conductivity had a good sensitivity to water content. For thermal conductivity method, at the all range of water content, the scatter points between measured and predicted values were on or near the 1:1 line, showing good predictions. For the maximum temperature rise and cumulative temperature rise methods, the scatter points were all around the 1:1 line when the water content range was in the 0-0.1 m3/m3, which had better prediction results, while the water content range was in the 0.1-0.25 m3/m3, where the scatter points were below the 1:1 line, which wound underestimate the moisture content. When the water content range was greater than 0.25 m3/m3, the scatter points were mostly above the 1:1 line, which overestimated the moisture content. The measurement accuracy of the thermal conductivity method was higher than that of the maximum temperature rise method and of the cumulative temperature rise method regardless of the low (0-0.1 m3/m3), medium (>0.1-0.2 m3/m3) and high (>0.2-0.35 m3/m3) water content ranges. The measurement accuracies of the 3 methods decreased with the increase of water content. The root mean square error of the thermal conductivity method was 0.015 m3/m3, which was lower than that of the maximum temperature rise method (0.038 m3/m3) and the cumulative temperature rise method (0.050 m3/m3). All of the 3 methods could measure soil water content accurately, but the accuracy of thermal conductivity method was the highest. However, although the maximum temperature rise and cumulative temperature rise methods could achieve certain accuracy, they had no physical meanings, the relationships between those 2 and water content were influenced by many factors, such as fiber optics characteristics and physical properties of soil. The thermal conductivity method had physical significance and was only related to the physical properties of soil. Moreover, the relationship between thermal conductivity and water content had been studied, and a lot of thermal conductivity models have been developed, which provided a simple and feasible method for estimating water content through soil thermal conductivity. Therefore, it was very attractive to measure water content by the active heating fiber optics-DTS using thermal conductivity method. This study provides guidance for water content measurement methods using DTS. It is of great significance to develop high-time-resolution in-situ monitoring techniques for soil water content at different spatial scales, and the ultimate goal is to accurately understand the water content dynamics in the field to guide the precision irrigation.

soils; water content; thermal conductivity; fiber optics;carbon-fiber; distributed temperature sensor

10.11975/j.issn.1002-6819.2019.10.006

S152.8

1002-6819(2019)-10-0042-08

2018-09-23

2019-03-10

国家自然科学基金项目（41601222、41630860）；西北农林科技大学基本科研业务费专项资金项目（2452017317）

胡优，博士生，主要从事分布式光纤测定土壤水热性质的研究。Email：hyagriwater@126.com。

司炳成，教授，主要从事土壤水文方面的研究。Email：bingchengsi@sina.com。

胡优，李敏，任姮烨，司炳成.基于加热光纤分布式温度传感器的土壤含水率测定方法[J]. 农业工程学报，2019，35(10)：42－49. doi：10.11975/j.issn.1002-6819.2019.10.006 http://www.tcsae.org

Hu You, Li Min, Ren Hengye, Si Bingcheng. Measurement of soil water content using distributed temperature sensor with heated fiber optics [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(10): 42－49. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.10.006 http://www.tcsae.org