基于自适应频率切片小波变换的滚动轴承故障诊断
2019-07-23马朝永盛志鹏胥永刚
马朝永,盛志鹏,胥永刚,2※,张 坤
基于自适应频率切片小波变换的滚动轴承故障诊断
马朝永1,盛志鹏1,胥永刚1,2※,张 坤1
(1. 北京工业大学先进制造技术北京市重点实验室,北京 100124;2. 北京工业大学北京市精密测控技术与仪器工程技术研究中心,北京 100124)
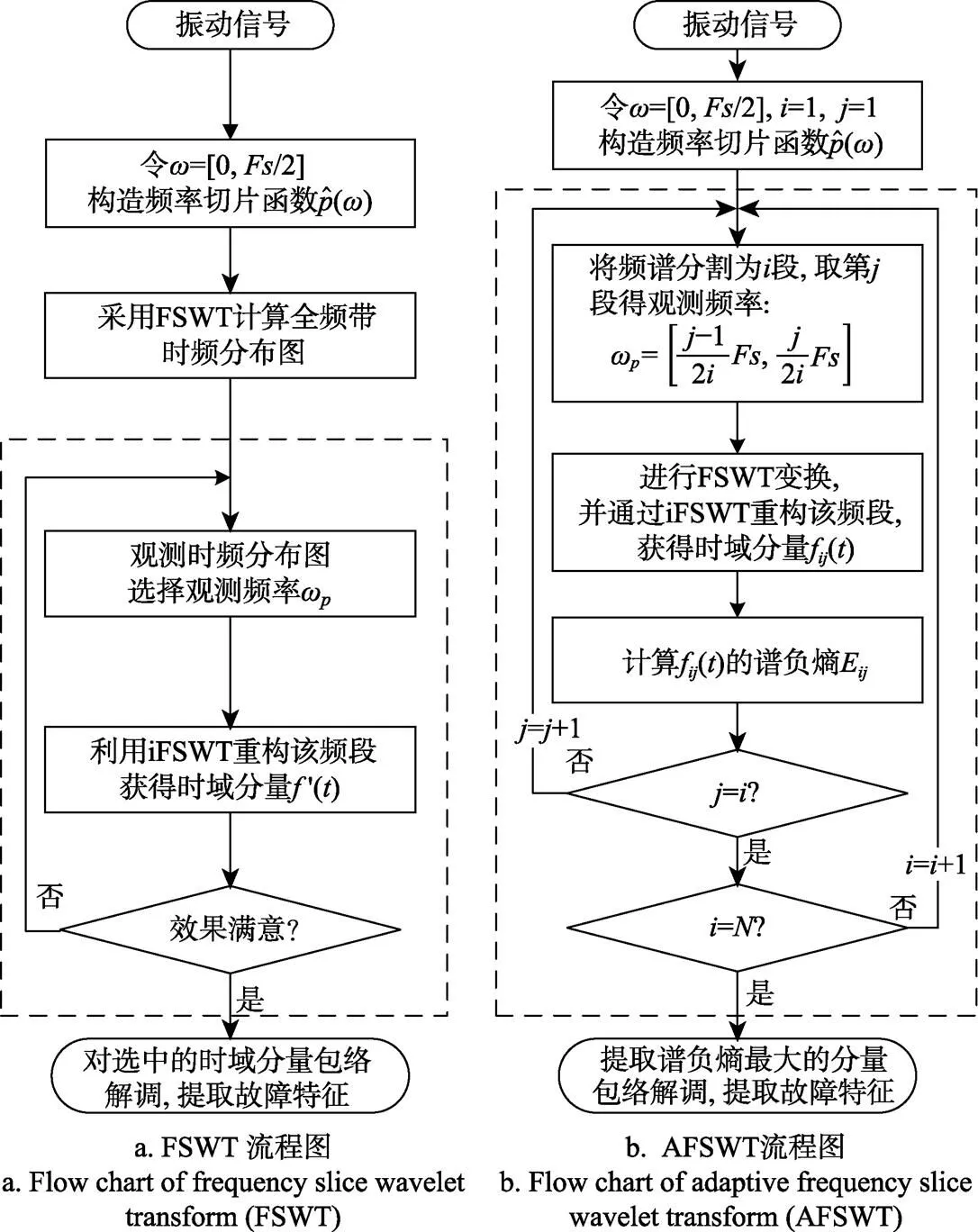
频率切片小波变换(frequency slice wavelet transform, FSWT)在汲取短时傅里叶变换和小波变换优势的基础上引入了频率切片函数,使传统的傅里叶变换实现了时频分析功能。FSWT通过对比不同频带处理的结果以确定最合适的中心频率及最佳带宽,实现了对信号任意频带及局部特征的重构及描述,但这种方法效率很低、无自适应性且无法保证手动筛选出的频段中包含所需要的故障信息。针对这个问题,该文提出一种自适应频率切片小波变换(adaptive frequency slice wavelet transform, AFSWT)。首先,连续分割信号的频谱,频谱分割覆盖了全频带且避免了手动选取频谱边界的过程,均分的方式可提高计算效率。其次,引入谱负熵作为评价依据,计算每一个频段内信号的复杂程度以筛选可能包含周期性冲击的循环平稳信息。最后,选取其中谱负熵最大的频段并将其定义为最佳的中心频率和带宽,重构该频段信号分量并包络解调分析,实现故障诊断。该方法均匀分割频谱并依据谱负熵筛选信号分量可以提高计算效率且提高筛选准确率。通过模拟信号及实验信号证明了该方法可应用于滚动轴承圈故障诊断。
轴承;振动;故障诊断;频率切片小波变换;谱负熵;频谱分割
0 引 言
轴承在旋转机械中应用十分广泛,同时由于滚动轴承常处于高温差、高压、高速运转等工况而极易损坏,从而导致耗时检修和紧急停车等事故[1-4]。因此,检测滚动轴承的运行状态并诊断其故障非常必要[5-7]。当滚动轴承出现损伤时所采集的振动信号常呈现非平稳、调制的特征,而且不可避免地会受到工业现场强噪声的干扰,识别故障特征十分困难。如何在复杂的非平稳、调制信号中有效提取携带故障特征信息的成分是诊断轴承故障的关键[8-9]。
近年来,非平稳信号处理方法,如短时傅里叶变换、Wigner-Ville分布、小波变换(包括连续小波变换、离散小波变换、双树复小波变换等)等具有坚实的理论基础,并且在机械设备故障诊断领域中发展迅速[10-13]。然而这些时频分析方法需要进行大量的前期准备工作,例如需要选择合适的窗函数或小波基函数等。因此以Huang等[14]提出的经验模态分解(EMD)为代表的一系列自适应信号分解方法出现并被迅速拓展[15-16],如局部均值分解、本征时间尺度分解、局部特征尺度分解法等。这类自适应分解方法完全由数据驱动并且可以将信号分解为一组模态分量。然而这些自适应方法普遍存在模态混叠、端点效应等不足。因此有学者对自适应方法进行了进一步研究,Gilles等提出从频谱提取模态信息,通过分割频谱并构造经验小波来重构每一个经验模态。该方法一定程度避免了由时域数据驱动产生的模态混叠及端点效应,但不合理的频谱分割结果会产生新的模态混叠及无效分量[17-18]。因此,很有必要从时域及频域同时展现信号特征并提取信号分量[19-20]。
Yan等[21-22]提出一种新的时频分析方法-频率切片小波变换(FSWT),该方法引入频率切片函数,使传统的傅里叶变换具有了时频分析的功能,不仅减少了小波和小波包在重构信号时对小波基函数的依赖,而且实现了信号在任意频带的重构及局部特征的精确描述,在各个领域均得到了广泛的应用[23]。段晨东等[24]将FSWT应用于炼油厂齿轮箱的故障诊断之中;Liu等[25]利用FSWT提高了梁结构损伤定位时的精度;杨仁树等[26]将EMD与FSWT结合应用于爆破振动信号中,在时域上获得了更高的时频分辨率;王元生等[27]将去噪源分离与FSWT结合,解决了旋转机械信号分析时产生的欠定盲源分离的问题。然而上述应用只能通过对比不同频带处理的结果以确定最合适的中心频率及最佳带宽,这种反复人为选频分析的过程耗费时间长,效率低且难以保证准确性,缺乏自适应性,非常有必要研究一种依据信号时频特性自适应选频的频率切片小波分析方法,以拓展该方法的应用领域。
为了使频率切片小波变换的选频过程更简便、高效,避免人为操作带来的不确定性,本文提出了自适应频率切片小波变换(AFSWT),采用预定义方式将频谱分割为若干等份代替原方法中手动选取;利用谱负熵评估各频段内循环平稳信息的强弱,筛选可能包含周期性冲击成分的频带以重构时频局部分量。
1 频率切片小波变换
1.1 频率切片小波变换原理
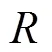
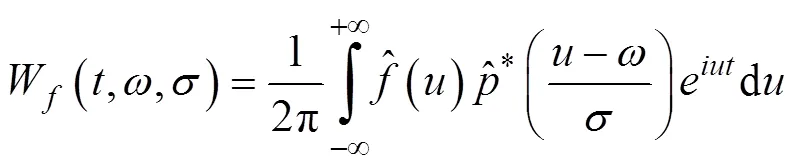
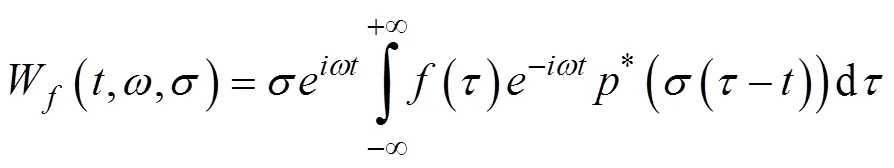
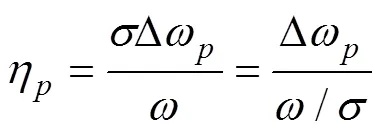
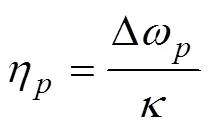
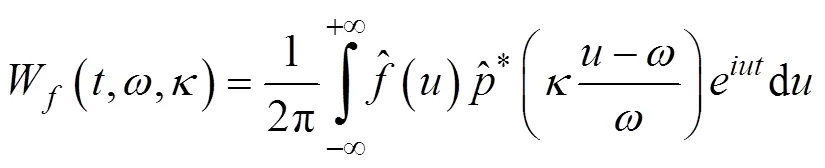
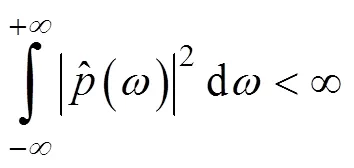
常用的2个切片函数为
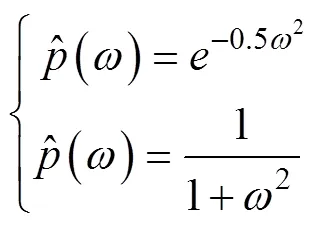
1.2 频率切片小波逆变换

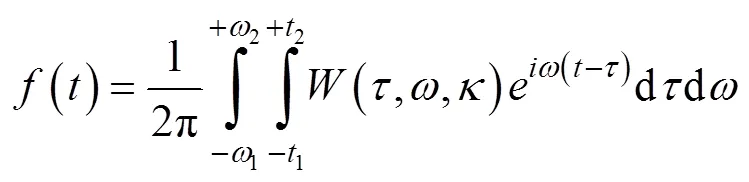
1.3 频率切片小波变换选频、重构与不足
该方法在实际应用中会遇到2个问题:其一,噪声的大小直接影响观测频率的选取范围。经验指定的方式难以保证结果的准确性。所以很有必要引入对研究对象故障特征敏感的指标来代替经验指定法。其二,手动选取频段的过程耗时低效,致使该方法难以应用于自适应或自动化领域。探索一种自适应频段提取法来代替手动选频法有重要的研究价值。本节构造一组仿真信号模拟滚动轴承外圈故障来展示FSWT的上述不足。
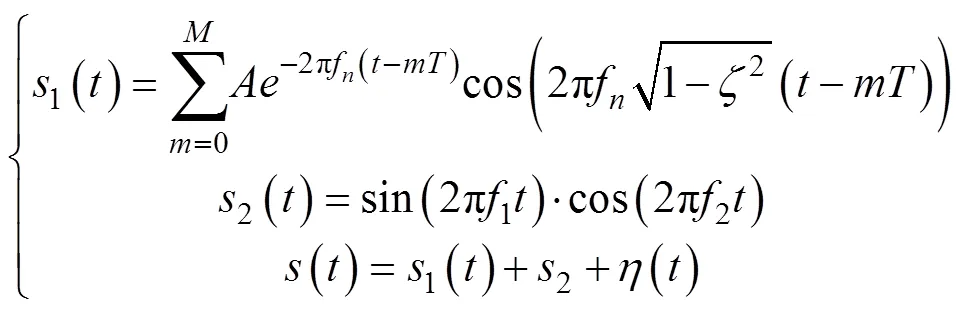
当冲击成分中加入调制成分和强噪声后,时域波形中的周期性冲击特征被噪声淹没,从时域中难以发现该信号中是否包含故障信息。从信号的频谱中可以看到,5 000 Hz附近出现边频带。根据共振解调原理,提取该频段可获得包含故障特征的信息。同时在该频段右侧6 000 Hz处有干扰信息。首先采用FSWT分析信号获得时频分布图,如图2所示。
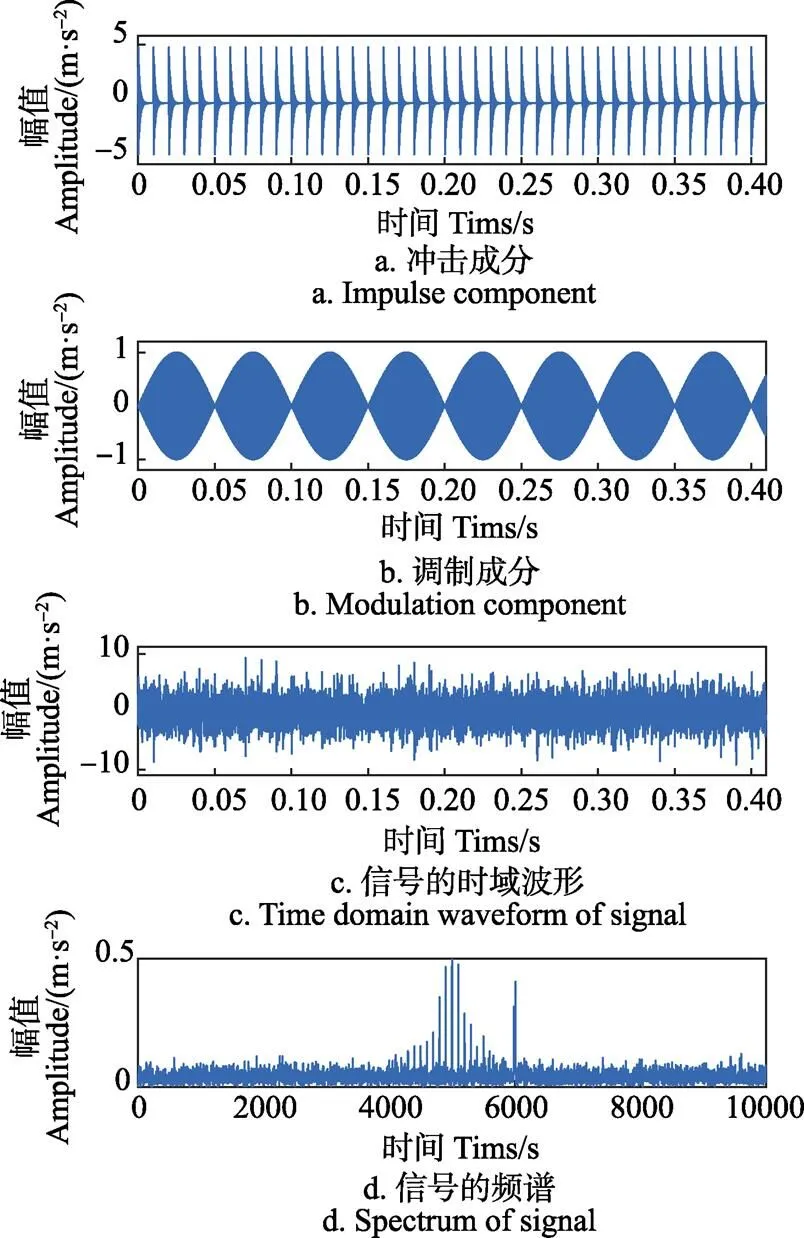
图1 仿真信号的时域波形及频谱
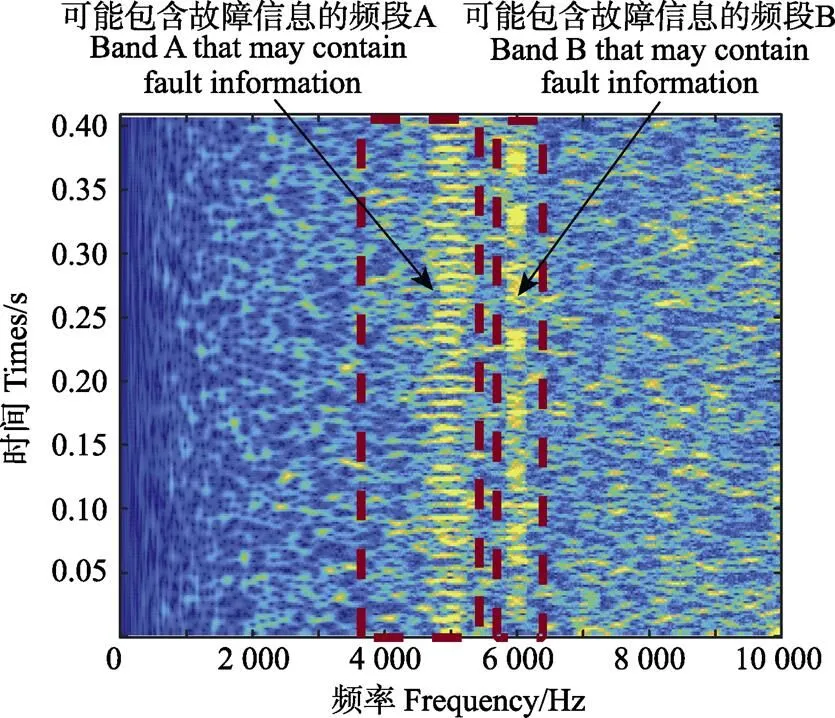
图2 FSWT时频分布图及经验指定的故障频段
由于信号中包含调制成分和强噪声,因此FSWT时频分布图中难以确定所选取频段的故障频段。经验指定法可能包含故障信息的频段见图2中的2个虚线框。左侧频段A有周期性幅值变化,但左右边界难以确定;右侧频段B幅值的周期性相对较差但左右边界比较明显。经验指定边界的方法需要反复试验以寻找故障频段,这给检测带来很大的工作量;如何从2个或多个频段中筛选出可能包含故障信息的频段需要进一步研究。因此,自适应确定故障频段及引入对周期性冲击信息敏感的指标筛选频段有着非常重要的研究价值。
2 自适应的频率切片小波变换
2.1 算法介绍
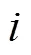
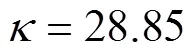
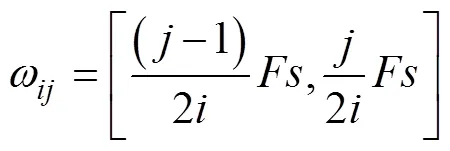
3)进行FSWT变换,并通过iFSWT重构频段,获得时域分量f()。
4)计算时域分量f()的谱负熵E,单位为bit。
6)提取f()中谱负熵最大的分量进行包络解调,提取故障特征。
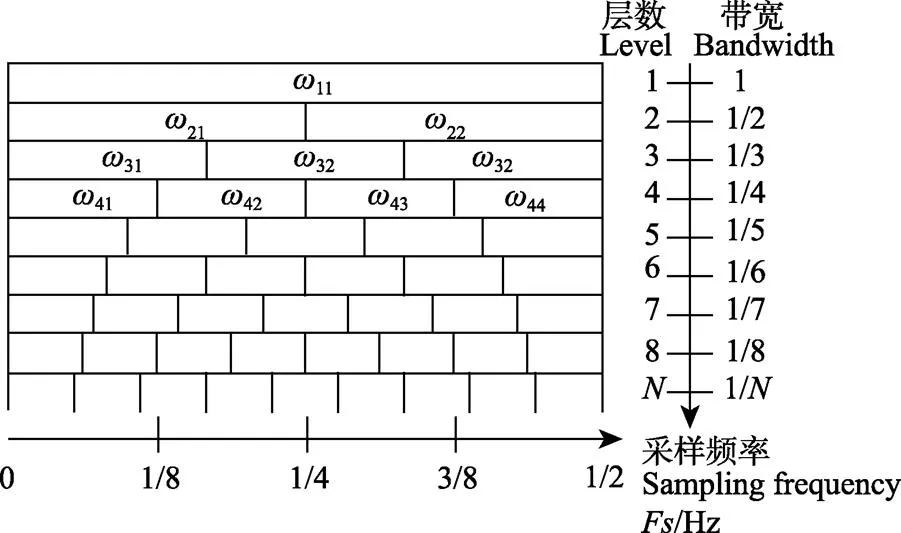
注:图中w11,w21,w22,w31…表示不同分解层观测频率的范围。
经验指定法FSWT和AFSWT流程图如图4所示。AFSWT方法利用FSWT重构特性自适应地连续分割频带并以谱负熵筛选出故障中心频率和带宽,取代了传统方法手动选取频带的过程,能够更准确、快速地提取故障特征。
2.2 谱负熵
旋转机械如滚动轴承发生故障时,振动信号中存在非平稳的周期性冲击信息,其特征可简单描述为脉冲和循环平稳。在故障诊断领域,信息熵可以用于衡量非平稳冲击成分在振动信号中的比重。基于此,Antoni[28-29]在谱峭度(spectral kurtosis, SK)、信息熵和包络谱的基础上扩展并将这些概念联系起来以捕获时域和频域中的周期性冲击信息。
注:w表示FSWT选取的频率区间,Hz;Fs表示采样频率,Hz。
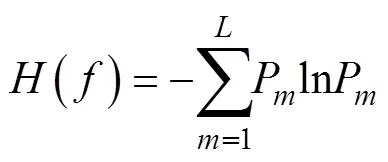
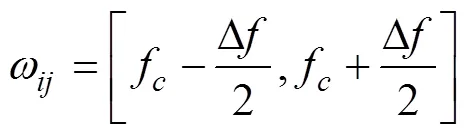
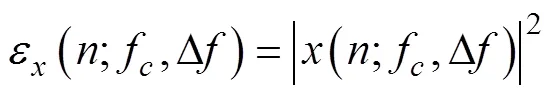
其平均值为
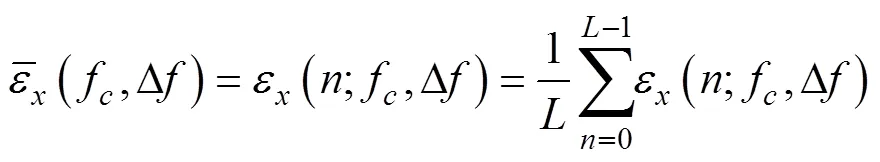
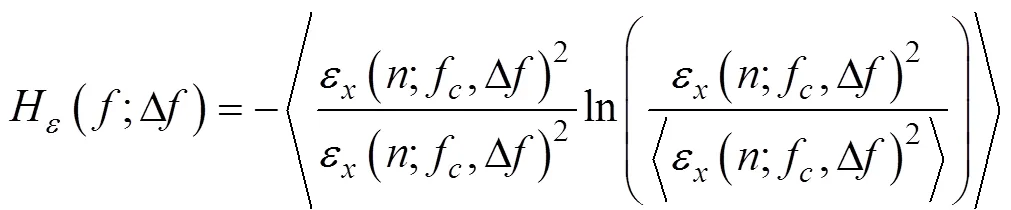
当能量流恒定时,可以得到最大谱熵,当能量流凝聚为单个脉冲时,可以得到最小谱熵。与快速谱峭度等自适应故障诊断方法相比,AFSWT采用信息熵替换峭度来识别冲击成分。因此本文提出了类似于谱峭度的信息熵:谱负熵(spectral negentropy)。其定义如下:
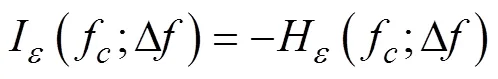
当滚动轴承发生故障时,振动信号中包含周期性冲击成分,该成分呈循环平稳特性且谱负熵对此敏感。基于此,本文应用谱负熵度量AFSWT提取的分量中包含周期性冲击的多少。
3 仿真信号分析
由于FSWT不具备自适应性,本文引入快速谱峭度(fast kurtogram, FK)并与自适应频率切片小波变换进行对比以验证提出的方法的有效性。FK由Antoni在深入研究谱峭度并给出正式定义后提出,并且广泛应用于滚动轴承故障诊断。采用FK处理公式(9)的仿真信号,获得谱峭度图,如图5a所示。
注:Kmax为最大峭度;Level表示层;Bw为带宽,Hz;fc为中心频率,Hz。下同。
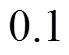
时域波形中的冲击有一定的周期性,但冲击特征不明显,从包络谱中能够分辨出特征频率及其2倍频。该方法选取的带宽较窄,中心频率有偏差,可能是导致冲击特征不明显的2个因素。采用本文提出的AFSWT处理该仿真信号,获得的快速谱负熵图如图6a所示。频谱被划分为16层,谱负熵最大的频段位于Level 11,左起第6个频段。其中心频率为f=5 000 Hz,带宽B=909 Hz,谱负熵为1.13 bit。提取该频段的分量,获得时域波形及包络谱,见图6c。时域波形中冲击的周期性较明显,包络谱中可找到特征频率和高倍频,故障特征明显。AFSWT提取的频段的中心频率为5 000Hz与1()的固有频率f相等。带宽约为快速谱峭度方法的2倍。因此该方法可找到更明显的冲击特征。
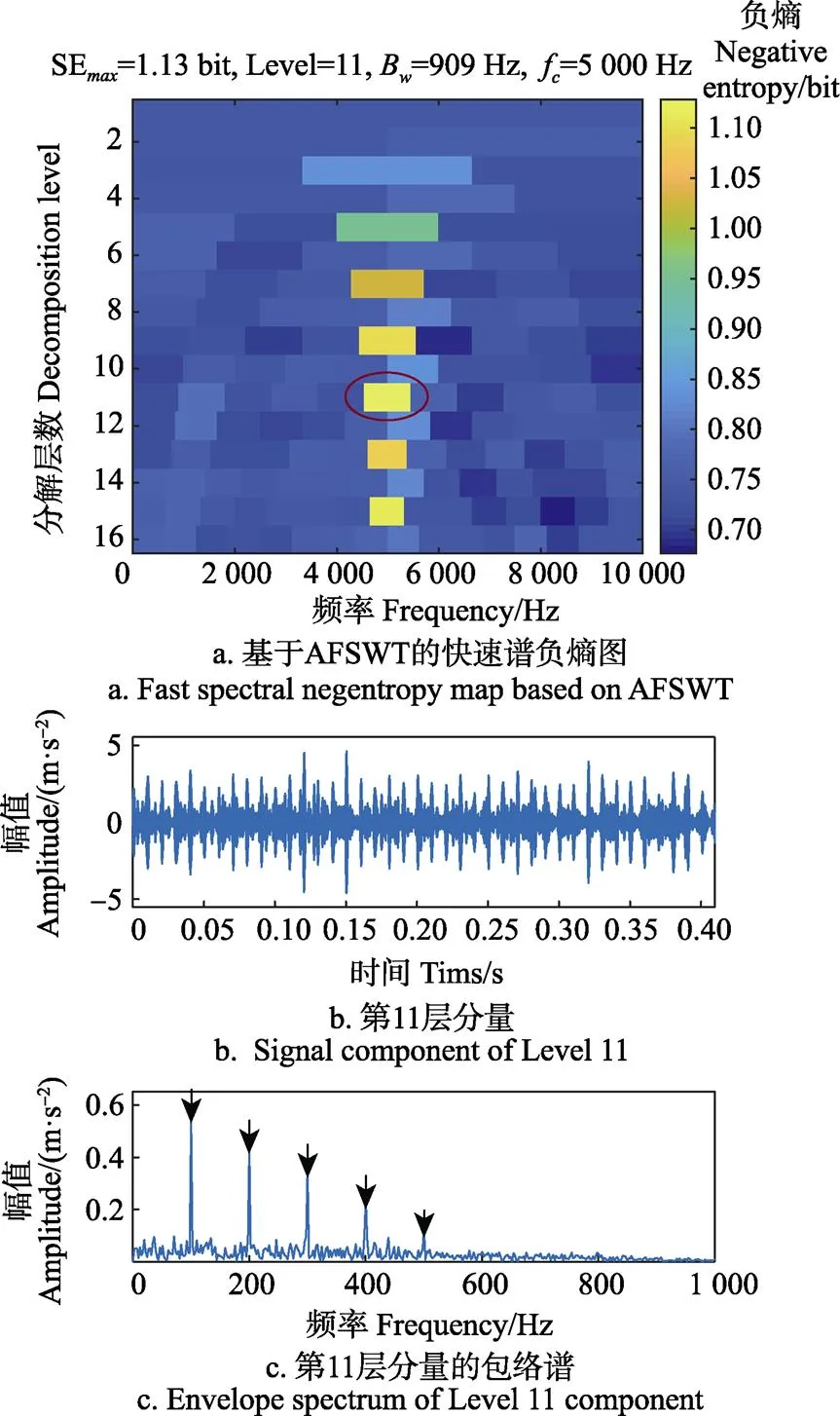
注:SEmax为最大谱负熵,bit;FSWT变换选取的切片函数为;尺度为k=28.85。下同。
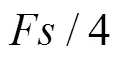
4 实例验证
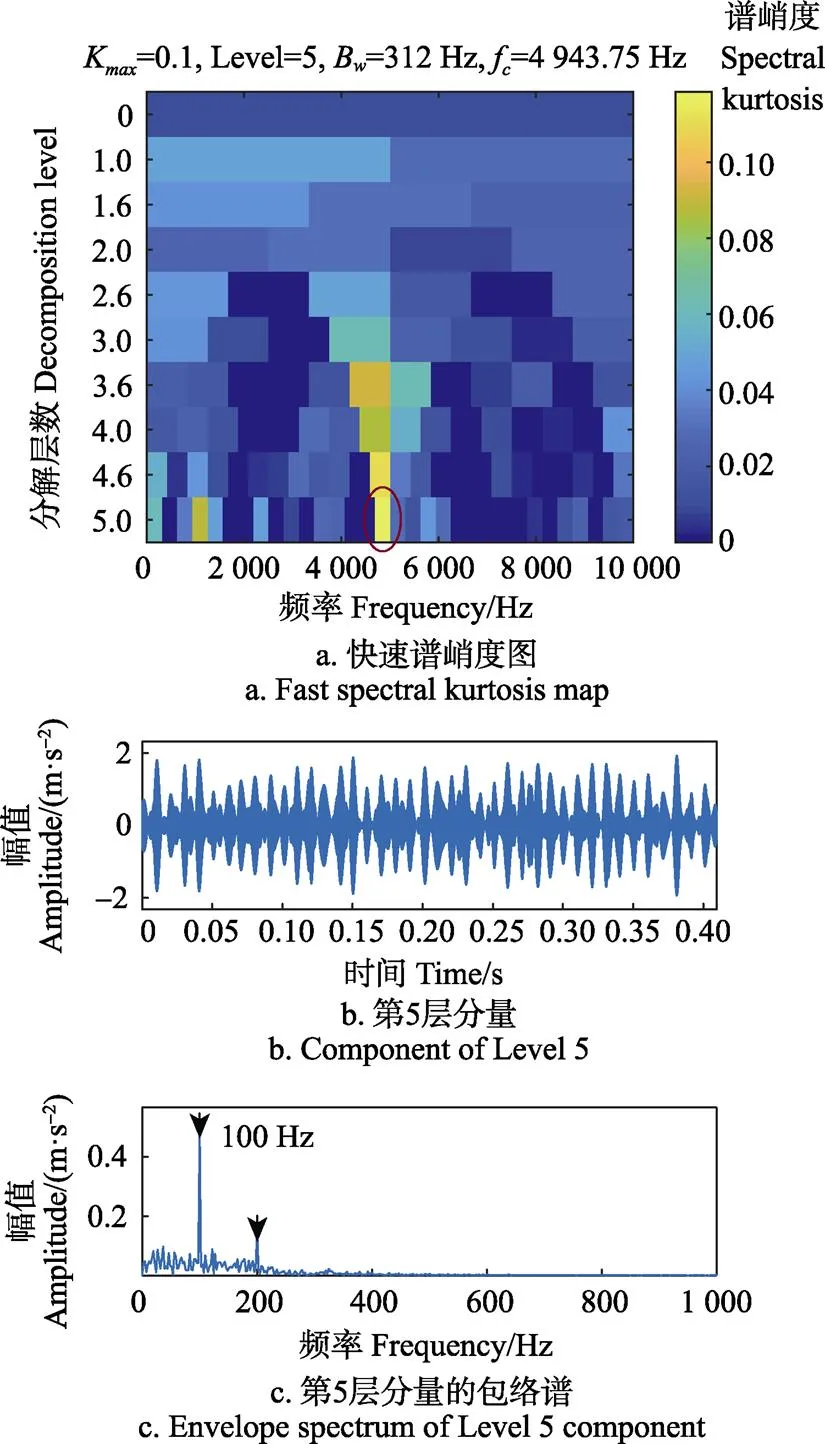
为了验证自适应频率切片小波变换方法的有效性,以6307型号滚动轴承为研究对象,对轴承外圈加工凹槽模拟故障,采用西安交通大学故障诊断实验室的滚动轴承试验台进行试验,如图7a所示。通过杭州亿恒科技有限公司的MI6008型数据采集仪、美国PCB公司的627A61型ICP加速度传感器和笔记本电脑采集滚动轴承的振动信号。根据6307轴承适用的工况,设置电机转速为1 450 r/min,采样频率为12 000 Hz,采样时间20 s。经计算,求得该轴承外圈故障特征频率为f=74.43 Hz。
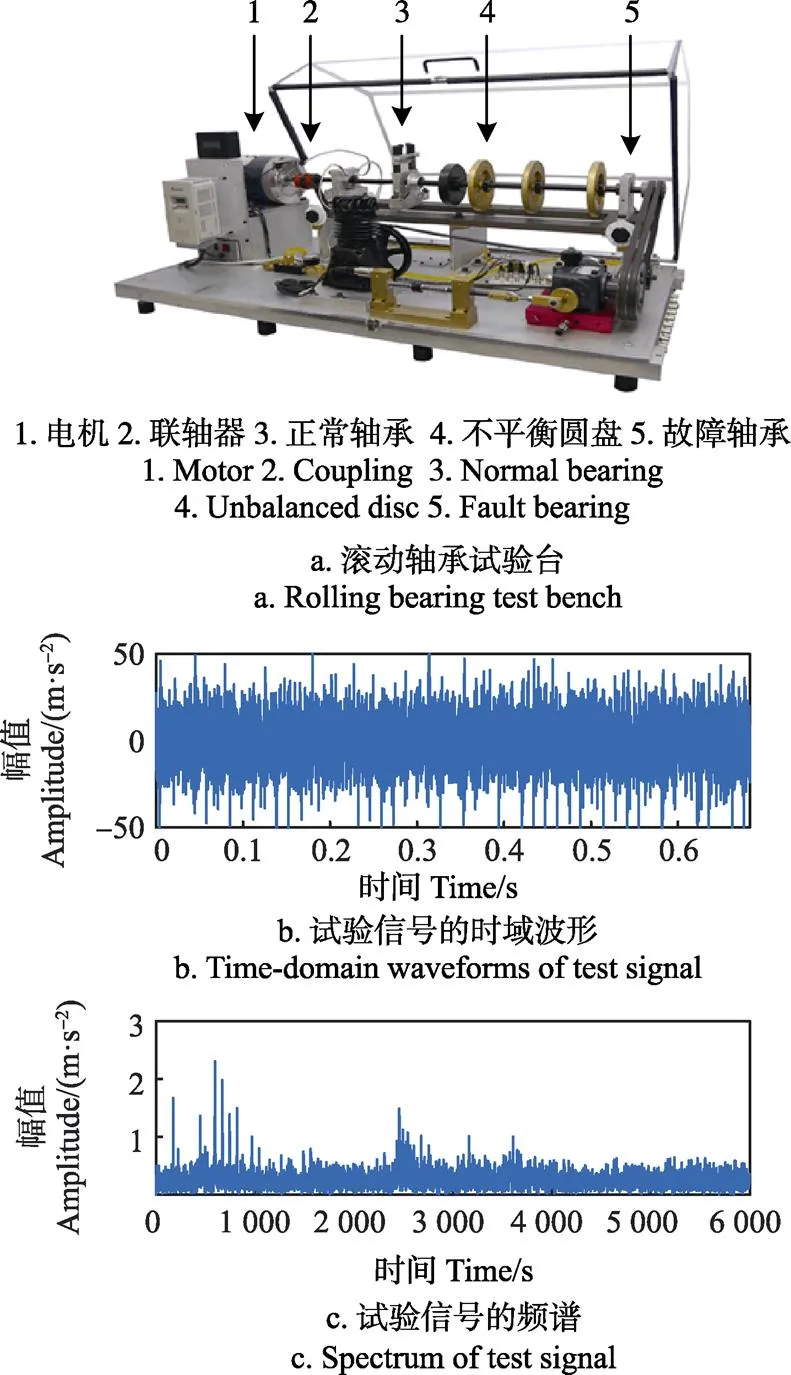
图7 试验设备及信号采集结果
便于进一步计算,截取振动信号中转速平稳的8 192个点进行分析,得到如图7b的时域波形。通过傅里叶变换得到信号的频谱图,如图7c所示。从时域波形中难以看出明显的周期性冲击现象,信号中包含故障的成分被强噪声淹没。从频谱图中也难以分辨出故障频率。因此需要对信号进行进一步处理。
采用自适应频率切片小波变换处理该试验信号,结果如图9a)所示。频谱被划分为16层,谱负熵最大的频段位于Level 8,左起第4个频段。其中心频率为f= 2 625 Hz,带宽B=750 Hz,谱负熵为0.89 bit。提取该频段的分量,获得时域波形及包络谱,见图9b和9c。
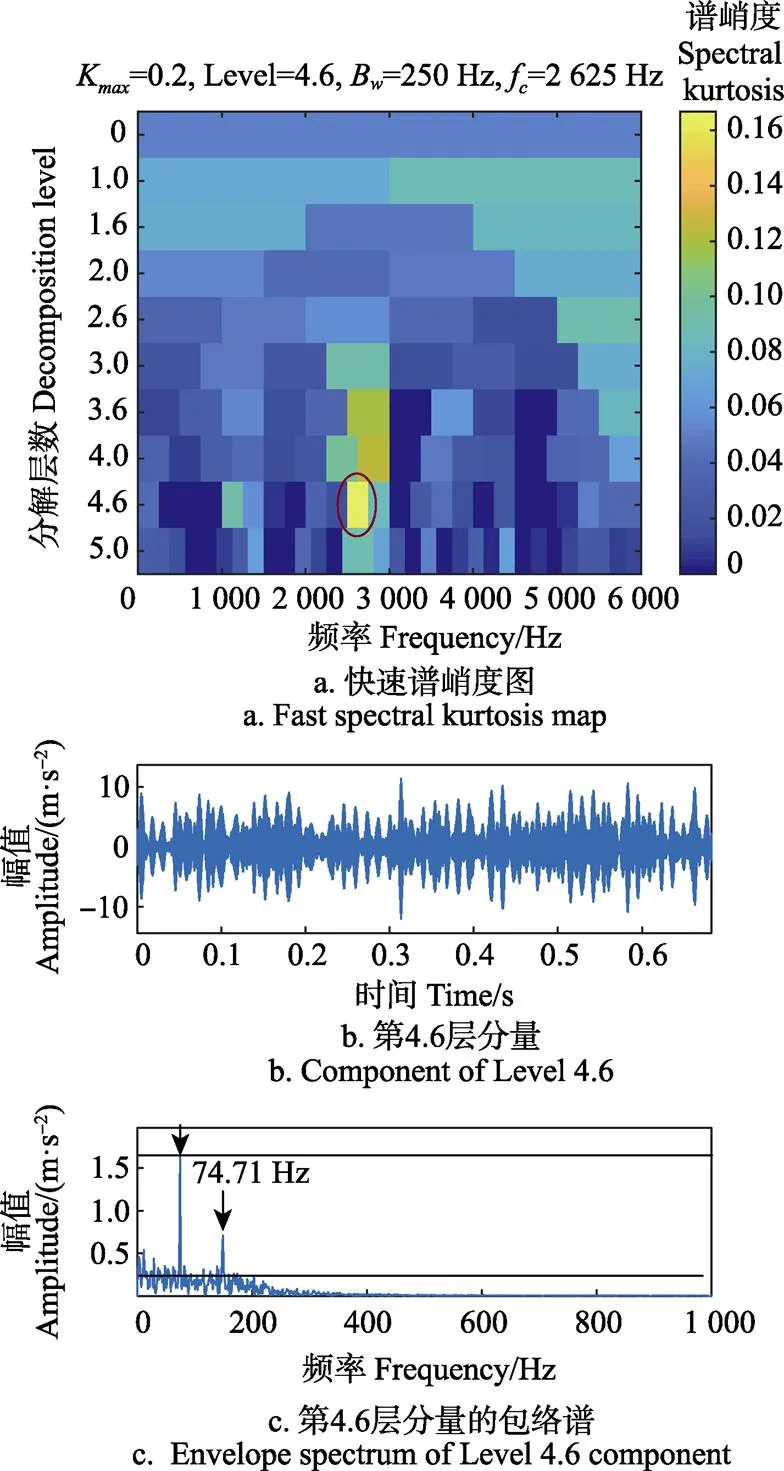
图8 试验信号的快速谱峭度处理结果
提取第8层分量得到的时域波形有一定的周期性但不明显,但是从包络谱中可找到比较明显的特征频率74.71 Hz及其2~6倍频,可以确定该轴承外圈发生故障。为了量化快速谱峭度和AFSWT方法的诊断效果,依据文献[30]引入故障频率检测精度指标:

根据图8c计算快速谱峭度方法的故障频率检测精度为1.69/0.227=7.44,而根据图9c计算AFSWT方法的故障频率检测精度为2.87/0.316=9.08,检测精度提升了22.04%。对比2种方法的包络谱和检测精度可知,AFSWT方法有更多的倍频成分和更高的检测精度,因此本文提出的自适应频率切片小波变换识别冲击特征的能力明显优于传统的快速谱峭度。此外,传统的频率切片小波变换依次经过计算时频分布图、寻找特征频带、反复确定观测频率等过程,往往需要5~10 min才能得到较为理想的诊断结果。分别运用快速谱峭度和自适应频率切片小波变换方法分析本节信号,运行过程耗时分别为25.7 s和14.7 s,自适应频率切片小波变换方法耗时更短,节省了42.8%的计算时间。
5 结 论
1)在滚动轴承的故障特征提取中,传统的频率切片小波变换方法依赖人工干预确定重构的频带,这种方法需要反复调整观测频带的范围,往往需要5~10 s才能提取出理想的频带。而经过本文提出的自适应频率切片小波变换方法处理试验信号,耗时14.7 s,该方法通过新的频谱分割方法改进频率切片小波变换,解决了手动选取观测频率的自适应性,实现了对振动信号的滤波和特征分离。
2)自适应频率切片小波变换采用对周期性冲击敏感的谱负熵解决了分量的选取问题,试验信号的处理结果表明,该方法的故障频率检测精度为9.08,较快速谱峭度检测精度提高了22.04%,且该方法得到的包络谱包含2~6倍的特征频率倍频,明显优于包络谱中仅有2倍频的快速谱峭度。说明该方法适用于滚动轴承故障诊断。
[1] Ali Jaouher Ben, Fnaiech Nader, Saidi Lotfi, et al. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals[J]. Applied Acoustics, 2015, 89(3): 16-27.
[2] 王志坚,韩振南,刘邱祖,等. 基于MED-EEMD的滚动轴承微弱故障特征提取[J]. 农业工程学报,2014,30(23):70-78. Wang Zhijian, Han Zhennan, Liu Qiuzu, et al. Weak fault diagnosis for rolling element bearing based on MED- EEMD[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(23): 70-78. (in Chinese with English abstract)
[3] Chen Jinglong, Pan Jun, Li Zipeng, et al. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals[J]. Renewable Energy, 2016, 89(1): 80-92.
[4] Xu Yonggang, Zhang Kun, Ma Chaoyong, et al. An improved empirical wavelet transform and its applications in rolling bearing fault diagnosis[J]. Applied Sciences, 2018, 8(12): 2352. DOI: 10.3390/app8122352
[5] 周士帅,窦东阳,薛斌. 基于LMD和MED的滚动轴承故障特征提取方法[J]. 农业工程学报,2016,32(23):70-76.Zhou Shishuai, Dou Dongyang, Xue Bin. Fault feature extraction method for rolling element bearings based on LMD and MED[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(23): 70-76. (in Chinese with English abstract)
[6] 陈志新,刘鑫,卢成林,等. 基于经验小波变换的复杂强噪声背景下弱故障检测方法[J]. 农业工程学报,2016,32(20):202-208. Chen Zhixin, Liu Xin, Lu Chenglin, et al. Weak fault detection method in complex strong noise condition based on empirical wavelet transform[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(20): 202-208. (in Chinese with English abstract)
[7] 向家伟,崔向欢,王衍学,等. 轴承故障诊断的最优化随机共振方法分析[J]. 农业工程学报,2014,30(12):50-55. Xiang Jiawei, Cui Xianghuan, Wang Yanxue, et al. Optimized stochastic resonance method for bearing fault diagnosis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(12): 50-55. (in Chinese with English abstract)
[8] 胥永刚,孟志鹏,赵国亮,等. 基于双树复小波包变换能量泄漏特性分析的齿轮故障诊断[J]. 农业工程学报,2014,30(2):72-77. Xu Yonggang, Meng Zhipeng, Zhao Guoliang, et al. Analysis of energy leakage characteristics of dual-tree complex wavelet packet transform and its application on gear fault diagnosis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(2): 72-77.(in Chinese with English abstract)
[9] Xu Yonggang, Zhang Kun, Ma Chaoyong, et al. Adaptive Kurtogram and its applications in rolling bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2019, 130(1): 87-107
[10] Wang Yi, Xu Guanghua, Liang Lin, et al. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2015, 54(1): 259-276.
[11] Liu Xin, Jia Yunxian, He Zeiwei, et al. Application of EMD-WVD and particle filter for gearbox fault feature extraction and remaining useful life prediction[J]. Journal of Vibroengineering, 2017, 19(3): 1793-1808.
[12] Chen Jinglong, Pan Jun, Li Zipeng, et al. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals[J]. Renewable Energy, 2016, 89(1): 80-92.
[13] Cao Hongrui, Fan Fei, Zhou Kai, et al. Wheel-bearing fault diagnosis of trains using empirical wavelet transform[J]. Measurement, 2016, 82(1): 439-449.
[14] Huang Norden E, Shen Zheng, Long Steven R, et al, The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.
[15] Li Yongbo, Xu MinQiang, Liang Xihui, et al. Application of bandwidth EMD and adaptive multiscale morphology analysis for incipient fault diagnosis of rolling bearings[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6506-6517.
[16] 窦东阳,杨建国,李丽娟,等. 基于EMD和MLEM2的滚动轴承智能故障诊断方法[J]. 农业工程学报,2011,27(4): 125-130.Dou Dongyang, Yang Jianguo, Li Lijuan, et al. Intelligent fault diagnosis method for rolling bearings based on EMD and MLEM2[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(4): 125-130. (in Chinese with English abstract)
[17] Gilles Jérôme. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010.
[18] Li Hongguang, Hu Yue, Li Fucai. Succinct and fast empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2017, 85(1): 879-895.
[19] Shi Juanjuan, Liang Ming, Dansorin Necsulescu, et al.Generalized stepwise demodulation transform and synchrosqueezing for time–frequency analysis and bearing fault diagnosis[J]. Journal of Sound and Vibration, 2016, 368(1): 202-222.
[20] Liu Ruonan, Yang Boyuan, Zhang Xiaoli, et al. Time- frequency atoms-driven support vector machine method for bearings incipient fault diagnosis[J]. Mechanical Systems and Signal Processing, 2016, 75(1): 345-370.
[21] Yan Zhonghong, Miyamoto Ayaho, Jiang Zhongwei. Frequency slice wavelet transform for transient vibration response analysis[J]. Mechanical Systems & Signal Processing, 2009, 23(5): 1474-1489.
[22] Yan Zhonghong, Miyamoto Ayaho, Jiang Zhongwei, et al. An overall theoretical description of frequency slice wavelet transform[J]. Mechanical Systems & Signal Processing, 2010, 24(2): 491-507.
[23] Biswal Birendra, Mishra Sukumar. Power signal disturbance identification and classification using a modified frequency slice wavelet transform[J]. IET Generation, Transmission & Distribution, 2014, 8(2): 353-362.
[24] 段晨东,高强. 基于时频切片分析的故障诊断方法及应用[J]. 振动与冲击,2011,30(9):1-5. Duan Chendong, Gao Qiang. Noval fault diagnosis approach using time-frequency slice analysis and its application[J]. Journal of Vibration Engineering, 2011, 30(9): 1-5. (in Chinese with English abstract)
[25] Liu Xinglong, Jiang Zhongwei, Yan Zhonghong. Improvement of accuracy in damage localization using frequency slice wavelet transform[J]. Shock and Vibration, 2015, 19(4): 585-596.
[26] 杨仁树,付晓强,杨国梁,等. EMD和FSWT组合方法在爆破振动信号分析中的应用研究[J] . 振动与冲击,2017,36(2):58-64. Yang Renshu, Fu Xiaoqiang, Yang Guoliang, et al.Application of EMD and FSWT combination method in blasting vibration signal analysis[J]. Journal of Vibration Engineering, 2017, 36(2): 58-64. (in Chinese with English abstract)
[27] 王元生,任兴民,邓旺群,等. 基于DSS和FSWT的欠定信号识别方法研究[J]. 振动与冲击,2014,33(21):80-84. Wang Yuansheng, Ren Xingmin, Deng Wangqun, et al. An efficient identification method for underdetermined signals based on DSS and FSWT[J]. Journal of Vibration Engineering, 2014, 33(21): 80-84. (in Chinese with English abstract)
[28] Antoni Jermoe. The infogram: Entropic evidence of the signature of repetitive transients[J]. Mechanical Systems & Signal Processing, 2016, 74(1): 73-94.
[29] Antoni Jermoe. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems & Signal Processing, 2007, 21(1): 108-124.
[30] 马增强,柳晓云,张俊甲,等. VMD和ICA联合降噪方法在轴承故障诊断中的应用[J]. 振动与冲击,2017,36(13):201-207. Ma Zengqiang, Liu Xiaoyun, Zhang Junjia, et al. Application of VMD-ICA combined method in fault diagnosis of rolling bearings[J]. Journal of Vibration Engineering, 2017, 36(13): 201-207. (in Chinese with English abstract)
Fault diagnosis of rolling bearing based on adaptive frequency slice wavelet transform
Ma Chaoyong1, Sheng Zhipeng1, Xu Yonggang1,2※, Zhang Kun1
(1.,,, 100124,; 2.,,100124,)
In industrial production, it is necessary to detect the running state of rolling bearings and diagnose their faults. When rolling bearing is damaged, the vibration signals collected often show the characteristics of non-stationary and modulation, and will inevitably be disturbed by strong noise, so it is very difficult to identify the fault features. How to effectively extract the components carrying fault feature information from complex non-stationary and modulated signals is the key of diagnosing bearing fault. Frequency slice wavelet transform (FSWT) uses frequency slice function based on the advantages of short-time Fourier transform (STFT) and wavelet transform (WT), which makes the traditional Fourier transform realize time-frequency analysis function. The traditional fault diagnosis method based on FSWT determines the most suitable center frequency and the faulty bandwidth by comparing the results of different frequency band processing, and realizes the reconstruction and description of arbitrary frequency band and local characteristics of the signal. However, this method is inefficient, non-adaptive and can not guarantee that the frequency band screened manually contains the required fault information. Aiming at the problem that traditional methods rely on manual operation and have no self-adaptability, an adaptive frequency slice wavelet transform (AFSWT) is proposed in this paper. Firstly, the signal spectrum is segmented continuously; spectrum segmentation covers the whole frequency band and avoids the process of manual selection of spectrum boundary. The method of equalization can improve the computational efficiency. Secondly, the spectral negative entropy is introduced as the evaluation basis to calculate the complexity of the signal in each frequency band in order to screen the cyclostationary information which may contain periodic shocks. Finally, the frequency band with the largest spectral negative entropy is selected and defined as the faulty center frequency and bandwidth. The signal components in the band are reconstructed and analyzed by envelope demodulation to realize fault diagnosis. The analysis results of a simulation signal show that the AFSWT method identifies the center frequency of 5 000 Hz and the bandwidth of 909 Hz, which is very close to the ideal result. Compared with fast spectral kurtosis, AFSWT has better applicability when the central frequency of signal is located in/4,/8 and/16(is the sampling frequency). Through the test of rolling bearing test-bench, the vibration signals of rolling bearing outer ring fault are collected and analyzed. After AFSWT analysis, the characteristic frequency and its 2-6 times frequency components can be clearly found in the envelope spectrum of the results. On the other hand, AFSWT takes 14.7 seconds to process test signals. The traditional FSWT needs repeated drawing of time-frequency distribution map, determination of central frequency band and selection of observation frequency, it often takes 5-10 minutes to determine the faulty center frequency and bandwidth. The above analysis shows that AFSWT can improve the calculation efficiency and screening accuracy by uniformly dividing the spectrum of the signal and screening the signal components according to the negative entropy of the spectrum. It is suitable for fault diagnosis of rolling bearings.
bearings; vibration; fault diagnosis; frequency slice wavelet transform; spectral negative entropy; spectrum segmentation
10.11975/j.issn.1002-6819.2019.10.005
TH133.3; TH165
A
1002-6819(2019)-10-0034-08
2018-12-29
2019-02-16
国家自然科学基金(51775005,51675009)
马朝永,副教授,博士,主要从事设备故障诊断方面研究。Email:machaoyong@bjut.edu.cn
胥永刚,副教授,博士,主要从事设备故障诊断方面研究。Email:xyg_1975@163.com
马朝永,盛志鹏,胥永刚,张 坤. 基于自适应频率切片小波变换的滚动轴承故障诊断[J]. 农业工程学报,2019,35(10):34-41. doi:10.11975/j.issn.1002-6819.2019.10.005 http://www.tcsae.org
Ma Chaoyong, Sheng Zhipeng, Xu Yonggang, Zhang Kun. Fault diagnosis of rolling bearing based on adaptive frequency slice wavelet transform[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(10): 34-41. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.10.005 http://www.tcsae.org
