上承式钢管混凝土拱桥地震响应分析

2019-07-20唐继舜陈远久

四川建筑 2019年6期

陶哲, 唐继舜, 陈远久

(西南交通大学桥梁工程系，四川成都 610031)

钢管混凝土拱桥以其跨越能力强，施工技术简易，造型美观等特点在我国得到了广泛的使用。自国内首座钢管混凝土拱桥——四川旺苍东河大桥于1990年建成以来，钢管混凝土拱桥在中国的研究与发展已经取得了相当丰富的成果，据统计至今已有400余座建成[1-2]。而地震灾害是工程建设中不可避免的问题，地震时建筑物的倒塌和破坏是造成人员伤亡和财产损失的直接原因。建筑物抗震性能如何，直接关系到受灾程度的高低，故必须作好建筑物的抗震设防工作，对钢管混凝土拱桥亦是如此。截至目前已有许多学者对钢管混凝土拱桥的抗震问题进行了研究，并取得了一些有价值的成果[3-7]。但与中下承式的拱桥结构相比，对上承式钢管混凝土拱桥地震响应行波效应分析的研究成果并不丰富。本文以某大跨度上承式钢管混凝土拱桥为分析对象，基于时程分析理论，使用桥梁空间有限元计算分析软件Midas/Civil分析其动力特性、包含行波效应在内的地震响应，旨在为同类型桥梁抗震设计提供参考。

1 工程概况

依据相关设计资料，某上承式钢管混凝土拱桥计算跨径为160 m，计算矢高为32 m，矢跨比为1/5，拱轴系数m=1.8。主拱采用两片四肢桁式拱肋，其中心距为6.25 m。单片拱肋由四根弦管组成，上下弦管高为3.2 m，左右弦管外边缘间距为2 m。主拱弦管为φ750×14 mm钢管(拱脚部位为φ750×16 mm钢管)，腹杆使用φ351×12 mm钢管。主拱在拱顶与拱脚共设置5道米字撑，与8道一字撑交替布置。弦管内灌注微膨胀混凝土，其余腹杆则均不灌注。拱上共设置立柱13对，为增加立柱的稳定性，采用钢管混凝土排架结构形式。其竖向主管使用φ351×12钢管，平联杆使用φ203×12钢管。上述钢材材质为Q345C，混凝土等级为C50。拱上行车道板采用14×12.25 m钢筋混凝土π型梁。全桥立面图和拱肋截面图见图1、图2。

2 有限元计算模型的建立

利用桥梁有限元分析软件Midas/Civil，基于空间杆系理论建立全桥空间有限元计算模型，如图3所示。其中钢管混凝土采用两种不同材料的钢管和混凝土梁单元共节点方式模拟，即双单元法。除桥面铺装使用各向同性的板单元模拟以外，全桥杆系结构均用空间梁单元模拟。拱肋与立柱采用共节点连接，立柱与盖梁采用刚性连接，主梁与盖梁间的板式橡胶支座采用弹性连接模拟，主跨上π型梁桥与引桥的连接处考虑伸缩缝的存在，释放其纵向约束，拱脚处固结。模型总计节点2 625个，单元6 005个。

计算模型所用材料参数见表1。

图3 有限元计算模型

3 抗震设防以及行波效应的模拟

依据该桥相关工程地质初勘报告以及设计文件，该桥主

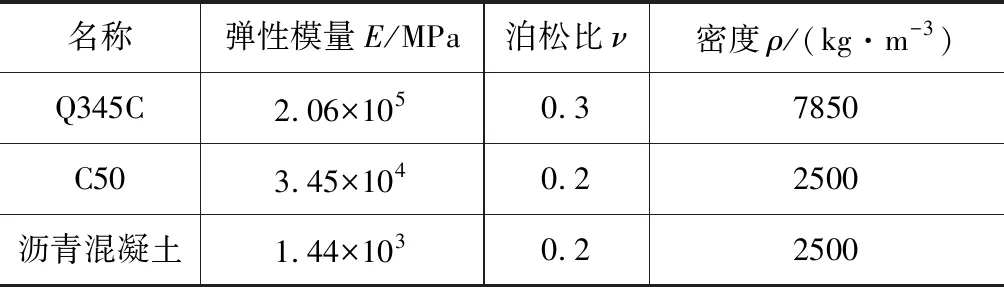
表1 相关材料参数表

跨跨径大于150 m，抗震设防类别为A类，场地类别为II类，地震设防烈度为9度(本文只进行E1地震作用下的相关研究)。

由于桥梁跨径较大，到达桥梁各支撑点的地震波所经历的传播路径、地质条件等并不一致，最终会导致各支撑点所受的地震波激励存在差异，这种差异主要表现为行波效应、局部场地效应、部分相干效应等。在Midas/Civil中主要的模拟方法包括对各支承点输入不同的地震波以及给予地震波到达各点时间的延迟的方式来处理[8]。现有研究表明，其中以行波效应的影响最为显著，即各支撑点输入地震波的相位差：

(1)

式中：δgo为原始地震波；c为地震波视波速；xi为i支承距第一支承点的直线距离。

对于本文的分析，考虑到地震动的随机性，场地因素，笔者依据公路桥梁抗震细则中的要求[9]：设计加速度时程不应小于三组，且需保证任意两组之间同方向时程由式(2)定义的相关系数ρ，其绝对值应小于0.1；地震波水平设计最大加速度为0.4g；竖向加速度与水平加速度比值R=0.5。

(2)

最终选取了符合特征周期、地震波幅值、持续时间要求(取20 s)的修正后的EI Centro波与两条人工波进行相关行波效应线性时程分析模拟，其中视波速取值分别为v=200 m/s、400 m/s、800 m/s。三条地震波如图4～图6所示。

图4 修正EI Centro波

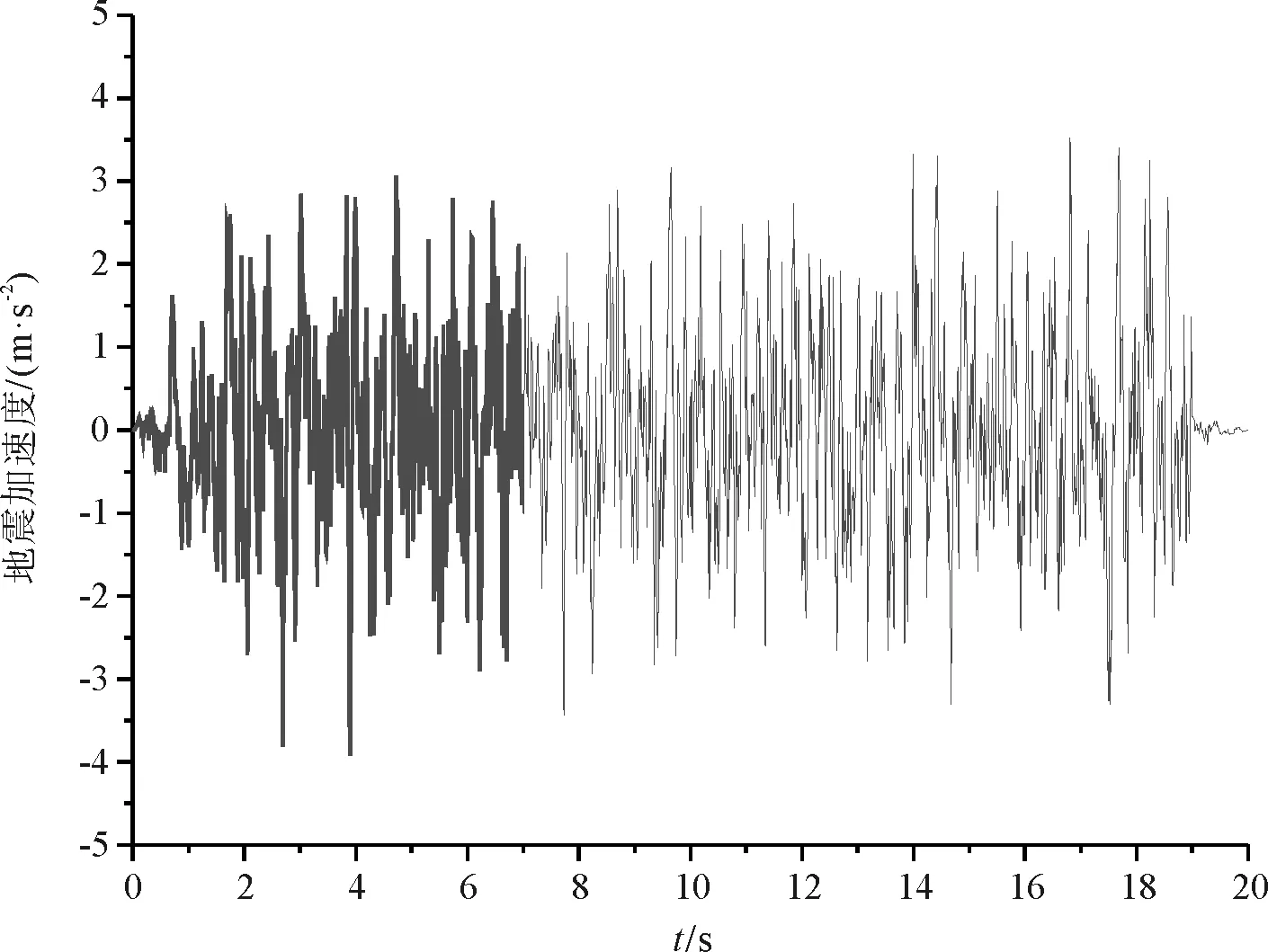
图5 修正人工波1

图6 修正人工波2

4 结构自振模态分析

掌握桥梁结构的自振特性是开展桥梁动力分析的基础与关键所在，为开展桥梁行波效应分析，首先应掌握结构的自振特性。对于本文的动力分析，利用子空间迭代法计算该桥的特征值，并以此得出结构前180阶振型，确保在X、Y、Z三个方向上的振型参与质量均大于90 %，其参与质量分别达到94.36 %、98.49 %、93.72 %。其中前8阶自振特性见表2。图7为结构前四阶振型图。

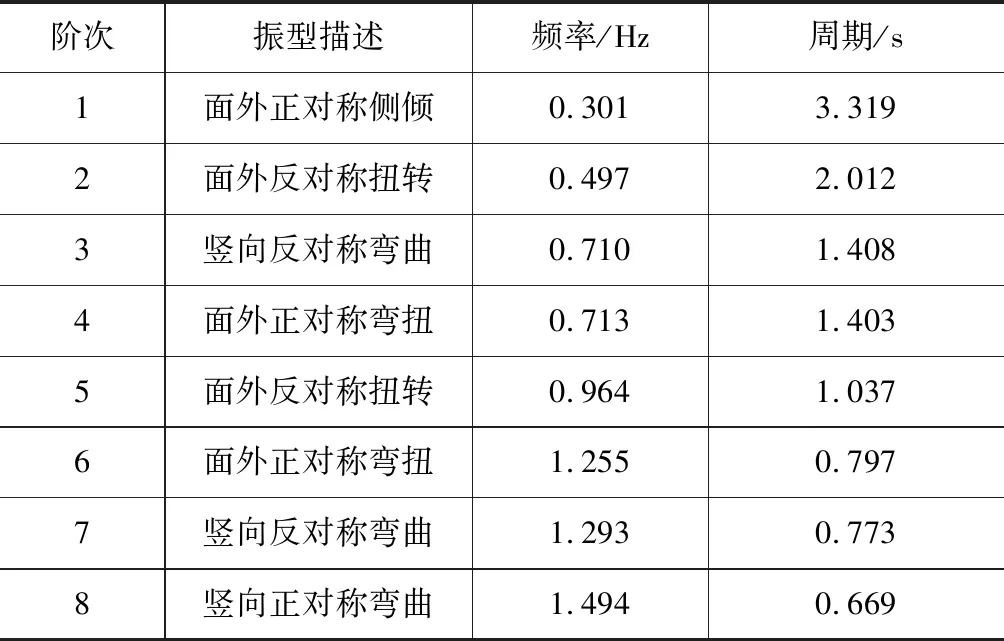
表2 桥梁结构自振特性表

(a)一阶振型

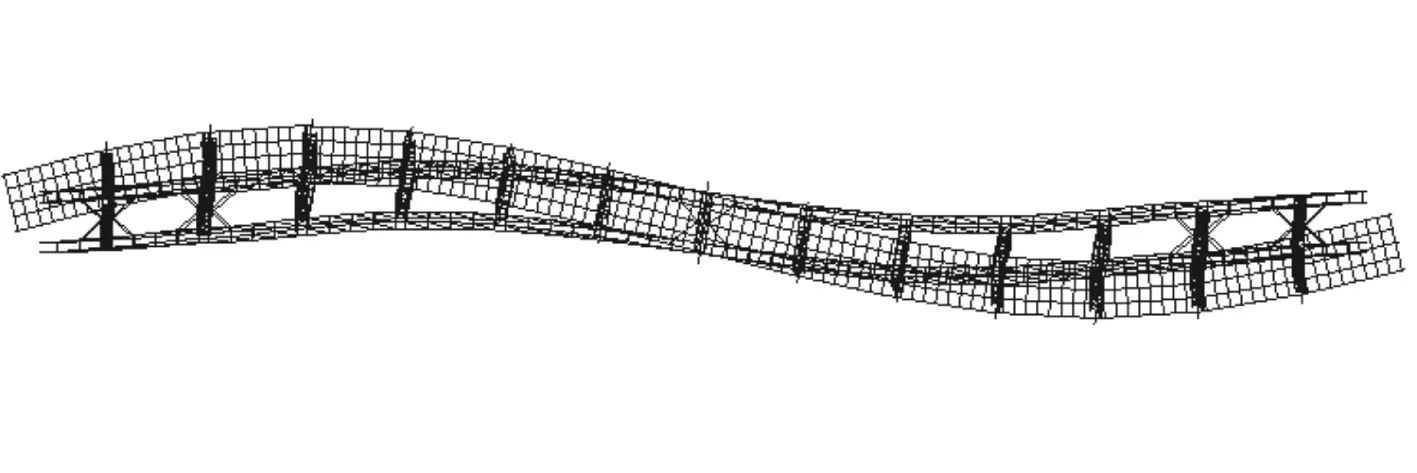
(b)二阶振型

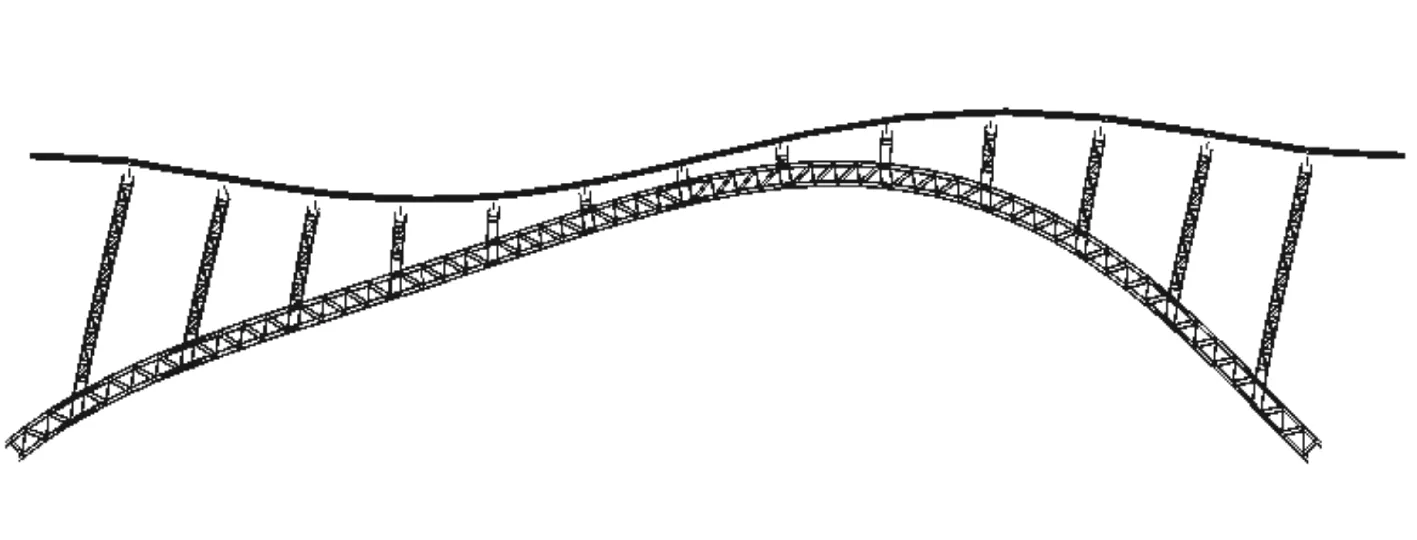
(c)三阶振型

(d)四阶振型图7 前四阶振型

(a)一和米字撑交替布置

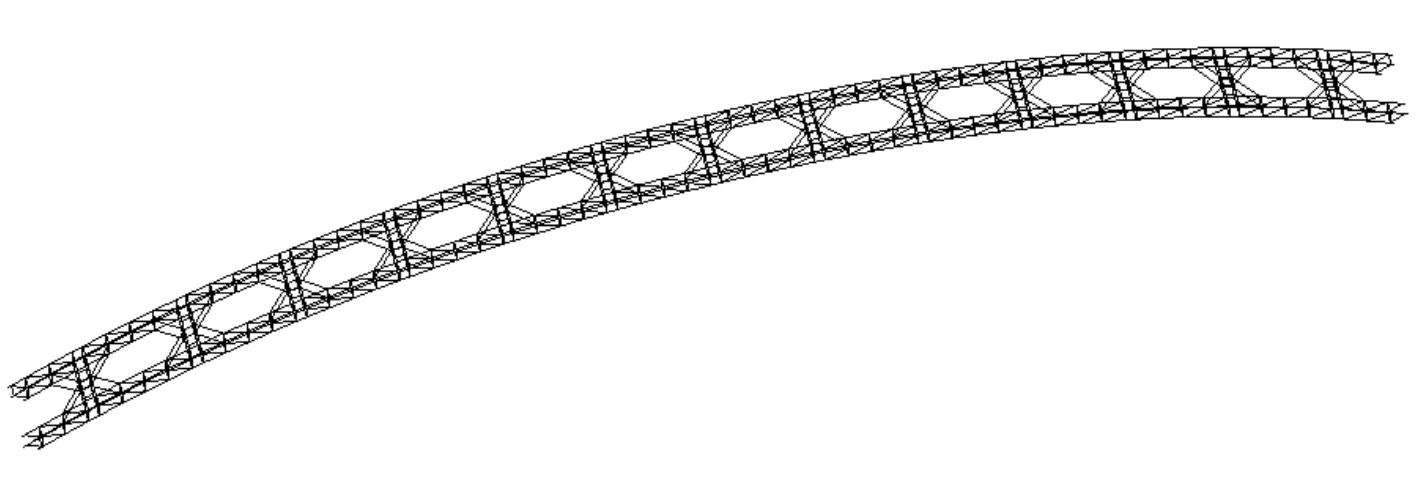
(b)全米字撑布置图8 两种拱肋横撑布置

该桥面外刚度较低，拟通过改变结构拱肋横撑形式来探究其对结构自振特性的影响。本文将原桥拱肋形式由一字撑与米字撑交替布置，改为拱肋横撑均采用米字撑形式，如图8所示。新结构同样利用子空间迭代法计算其特征值，并以此得出结构前180阶振型。在X、Y、Z三个方向上的振型参与质量分别达到94.38 %、98.52 %、93.74 %。两种横撑形式桥梁自振特性如表3所示。

由上述两种结构自振特性分析结果可以得出以下结论：

(1)该上承式钢管混凝土拱桥结构的基频仅为0.301 Hz，略大于大跨度斜拉桥与悬索桥的基频(一般小于0.2 Hz)，而又小于刚性拱桥的基频，属于中高柔性结构。

(2)前8阶振型以面外振型为主，竖向振型次之，表明该种桥梁结构面外刚度较面内刚度更小，纵向刚度则最大。结构面外稳定问题突出。

(3)可以通过改变拱肋横撑形式来提高结构横向刚度，将原结构拱肋横撑的布置形式由一字撑与米字撑交替布置改为全采用米字撑布置，其结构基频较原结构提升了25.25 %。

(4)拱上立柱刚度较大，可以看出主拱上π型梁桥与主拱肋的振动保持一致性。

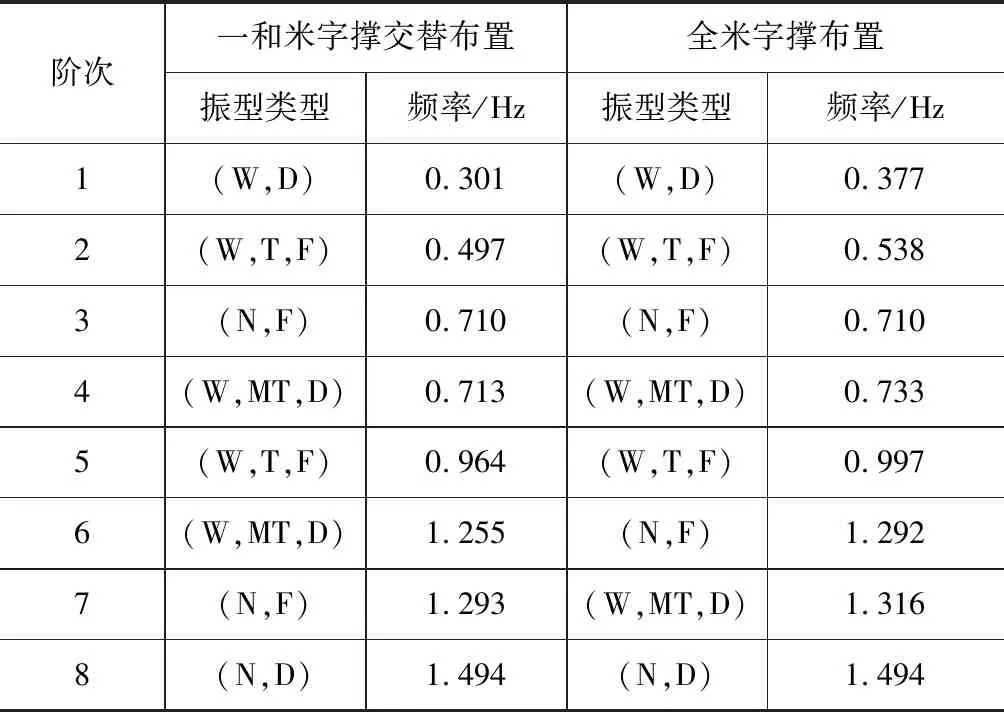
表3 两横撑结构自振特性表

5 结构抗震计算结果与分析

现有工程结构的地震响应计算手段为反应谱法以及时程分析法。其中动态时程分析法属于瞬态动力学分析计算方法，可确定地震荷载激励下结构位移、应力等随时间的变化关系。其可进行结构线性或非线性地震响应的分析[10]。

本文使用时程分析法(线性)对该桥梁结构的相关地震响应进行分析，对所选用三条地震波计算分析结果以包络形式取值，分析主要包含的计算工况见表4。

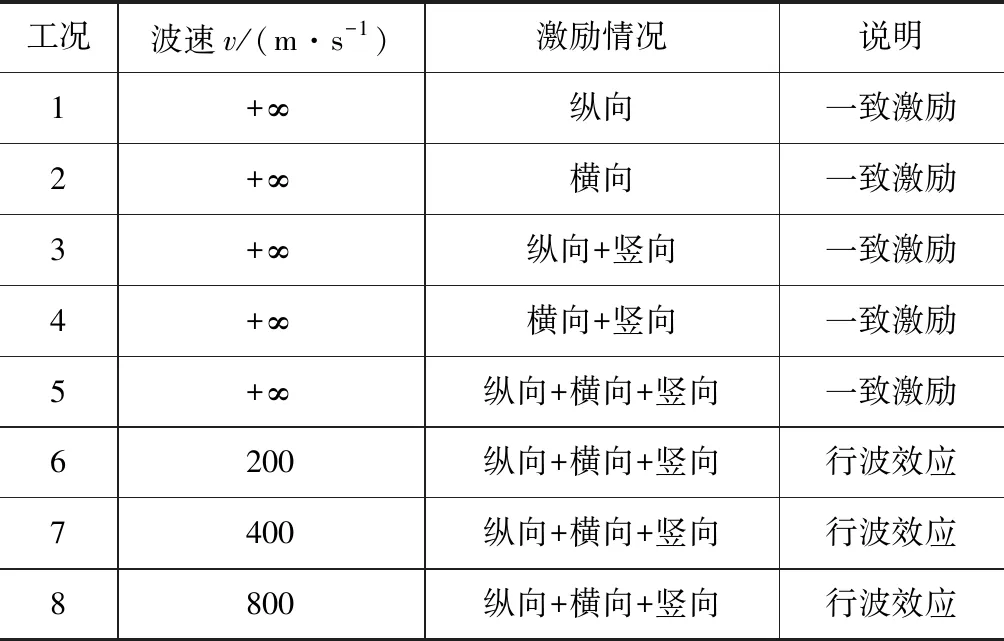
表4 地震响应计算工况表

进行有限元仿真分析后，得出上述各工况下主拱拱肋主要控制截面受力情况，如表5、表6所示。

将纵向+横向+竖向三维地震波一致激励工况的受力分析数值结果作为基准值，做出各工况地震波激励下各控制截面轴力、弯矩大小的比值结果，并绘制相关折线图，如图9、图10所示。

综合8种工况下有限元软件Midas/Civil仿真分析结果，并结合不同地震激励工况下拱肋控制截面弯矩、轴力，以及各工况下拱肋控制截面弯矩、轴压力比值，可以得出以下结论：

(1)各型地震激励下，考虑行波效应与否，对于某一地震激励下拱肋的最大弯矩、最大轴压力值均出现在拱脚位置处。

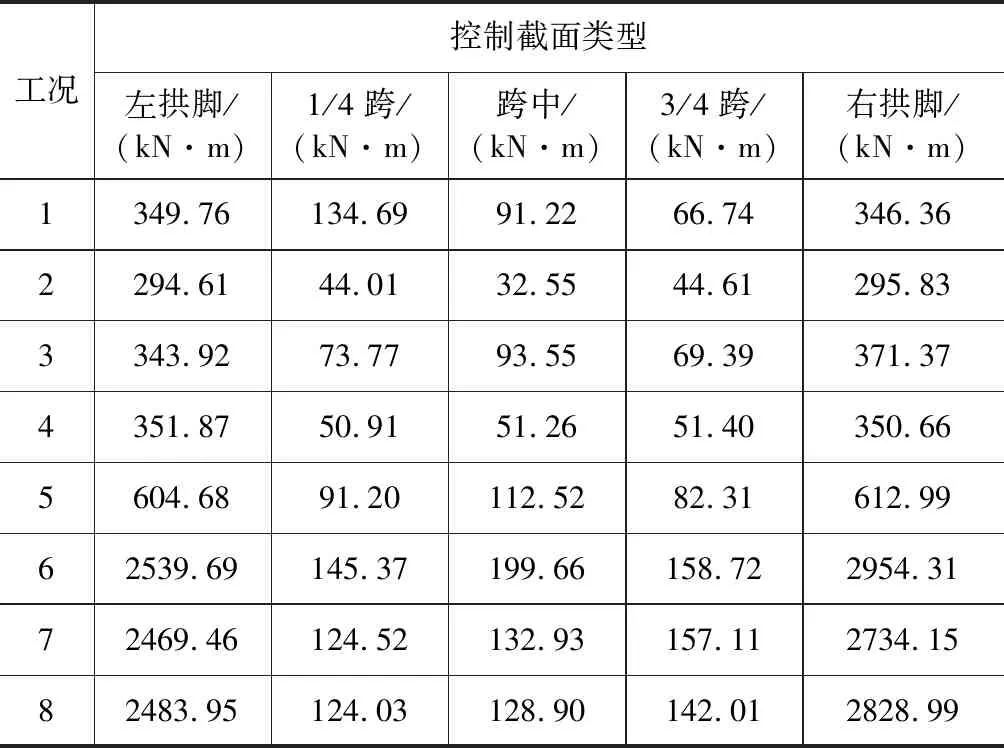
表5 不同地震激励下拱肋控制截面弯矩值

图9 各工况下拱肋控制截面弯矩比值

图10 各工况下拱肋控制截面轴压力比值

(2)在一、二维地震波同步激励下，相关桥梁结构各控制截面的最大弯矩与轴压力值较为接近，但在三维同步激励下，其数值有一定幅度的提升，且拱脚截面处地震反应内力的提升幅度大于1/4跨、拱顶、3/4跨截面。与一、二维地震波激励下拱肋拱脚截面处最大弯矩、轴压力相比，三维同步地震波激励下拱肋控制截面最大弯矩、轴压力分别提升了65.06 %以及25.92 %，弯矩的提升幅度大于轴压力。

(3)考虑行波效应的三维地震波激励相比与三维一致激励，其地震响应弯矩与轴压力值在拱肋1/4跨、3/4跨截面很接近，没有很大程度的改变，但是在拱脚与拱顶截面确有很大幅度的提升，尤其是在拱脚截面处。在视波速取值为200 m/s的地震响应行波效应工况下，该桥右拱脚截面地震响应弯矩值提升至4.82倍，左拱脚截面地震响应轴压力值提升至3.52倍。

(4)不同波速取值的考虑行波效应的地震激励的结果有所差异，且与波速大小没有直接关系，比较复杂。因此在抗震分析中对行波效应视波速的取值问题应专项研究。