基于Normal分布的岩石统计热损伤本构模型研究

朱振南，蒋国盛，田红，吴文兵,2，梁荣柱,2，窦斌

(1.中国地质大学(武汉)工程学院，湖北 武汉，430074；2.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州，310058)

随着高放核废料地下深埋处置、干热岩地热资源开发和矿产资源深部开采等高温岩体工程的进一步发展，人们对高温作用下或高温作用后岩石物理力学特征的相关研究越来越多。与常温状态下相比，高温下或高温后岩石的力学性质通常会发生劣化，进而影响地下高温岩体工程的稳定与安全。研究者从不同角度和层次，通过宏观及微观试验研究了温度对岩石物理力学性质的影响。通过宏观力学试验研究发现花岗 岩[1-3]、大理岩[4-6]、砂岩[7-9]、黏土岩[10]等的力学性能如弹性模量、抗压强度随温度升高而呈现出弱化的趋势。PENG等[11-13]利用扫描电子显微镜(SEM)观测得出，不同岩石内部的微裂纹会随温度的升高而不断生成、扩展、增多，并且微裂纹类型由晶间裂纹逐渐转变为穿晶裂纹。这些试验研究揭示了温度对岩石具有热损伤作用，因此，在高温岩体工程设计与计算中，为了更精确地描述岩石的力学行为，采用考虑温度效应的岩石本构模型十分必要。目前，考虑温度作用的本构模型主要分3 大类：1)基于损伤理论和热弹性理论建立的热弹塑性损伤模型[14-16]；2)基于蠕变试验和热黏塑性理论建立的流变模型[17-18]；3)基于统计分布建立的岩石热损伤本构模型[19-20]。统计损伤本构模型可以直接而又准确地描述岩石损伤演化过程的缺陷，从而更好地刻画岩石损伤的力学机制，因而该类模型较前2 类模型具有明显的优势。在岩石统计损伤本构模型[21-26]的基础上，徐银花等[19]通过考虑温度对统计参数的影响建立了高温下岩石损伤本构模型，但仅考虑了单向压力，对三向应力状态的适用性没有进一步验证；李天斌等[20]通过考虑温度对统计参数的影响建立了考虑温度启裂应力的热-力-损伤本构模型，但未验证其高温的适用性。为此，本文作者在传统岩石统计本构模型基础上，假设受热损伤的岩石微元强度服从Normal分布，引入热损伤变量，建立满足Mohr- Coulomb 准则的岩石统计热损伤本构模型。通过与高温作用后花岗岩单轴和三轴压缩试验结果进行对比，验证所提模型的合理性和适用性。

1 模型建立

1.1 本构关系和损伤变量

岩石内部含有微裂隙和孔洞等天然缺陷，高温作用后会引起这些缺陷不断破坏、连接和贯通。依据损伤理论，高温对岩石的损伤为统计损伤，受热损伤的岩石微元体强度服从统计分布。本文在常温损伤变量D定义[22]的基础上，提出热损伤变量DT，为岩石经历高温作用后在某一应力状态下已破坏微元体数目NTf与总微元体数目NT的比值，即

假设经高温作用后微元体强度概率密度函数为P(FT)，当应力水平FT超过一定强度时，单元相继破裂。在区间[FT，FT+dFT]内，若新破坏的微元体数目为N(FT)dFT，则DT为

高温作用后，岩石在荷载作用下，应变等效性假设示意图如图1所示(其中，A为岩石初始横截面总面积，A*为岩石受损后的有效承载面积，A-A*为在加载过程中出现损伤后的截面面积)。由式(1)可得

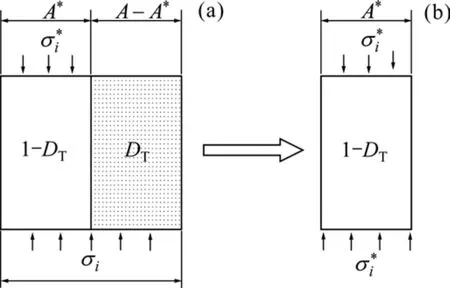
图1 应变等效性假设示意图Fig.1 Illustration of strain equivalence hypothesis

根据Lemaitre 应变等价理论和有效应力的概 念[27]，此假说认为名义应力下含损伤岩石产生的应变等价于有效应力下含损伤岩石产生的有效应变(其中名义应力即为试验测的应力)，则考虑温度作用后含损伤的名义应力iσ(i=1，2和3)和有效应力和3)的关系为

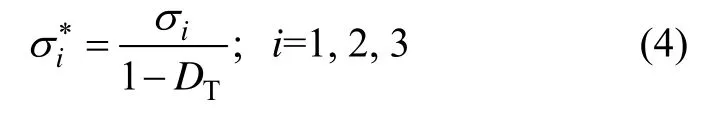
经历高温作用后岩石应力-应变曲线依然存在明显的弹性阶段[10]，且力学参数(弹性模量E、泊松比v)受温度影响[1-10]。设依赖于损伤温度的弹性模量和泊松比分别为ET和vT，并假定高温作用后未受损伤的岩石部分处于完全弹性状态，则根据广义胡克定律可知

式中：(i，j，k)为(1，2，3)，(2，3，1)或(3，1，2)；和分别为不同温度作用后岩石有效弹性模量和有效泊松比；为与有效应力所对应的有效应变。

由式(4)和(5)可得

根据Lemaitre 应变等价理论可得

其中：εi为与有效应力σi所对应的名义应变。岩石弹性模量定义为岩石处在弹性阶段轴向应力和轴向应变之比，因此，可认为

将式(4)，(7)～(9)代入式(6)可得出

对式(10)进行简化可得到岩石材料经历热损伤作用的各向同性弹性损伤本构方程：

式中：(i，j，k)为(1，2，3)，(2，3，1)或(3，1，2)；ET和Tv分别为岩石经历不同温度作用后的弹性模量和泊松比。对于含初始损伤的岩石，DT的取值范围为0≤DT≤1，其中，DT=0 表示岩石材料未经高温作用处于初始无损状态，DT=1 表示岩石材料经高温作用后处于完全损伤状态。

应用此热损伤本构方程时，需要着重考虑以下2个问题：1)高温作用后岩石微元体应力水平FT的确定；2)高温作用后微元强度概率密度函数P(FT)的选择。

1.2 应力水平

经高温作用后岩石微观破坏准则可用有效应力和岩石材料参数表示：

式中：KT为与经高温作用后岩石材料参数有关的常数；*σ为岩石内部微元体的有效应力。当时，岩石微元单元产生破坏，因此，可以作为微元体应力，用来反映岩石微观破坏程度，即

曹文贵等[22]提出基于岩石破坏准则的新型岩石微元强度度量方法，该方法能直接反映应力状态对岩石微元强度的影响。试验结果表明，岩石的内摩擦角随温度的升高而增大，黏聚力随温度的升高而降低[2]。Mohr-Coulomb 准则具有参数形式简单且适用于岩石介质等特点，利用有效应力和岩石力学参数表示的考虑温度效应的Mohr-Coulomb 准则[28]可表示为

式中：Tφ和cT分别为依赖温度的岩石内摩擦角和黏聚力；(i=1，2和3)为有效应力下3 个主应力分量。因此，经高温作用后岩石微元应力水平FT可表示为

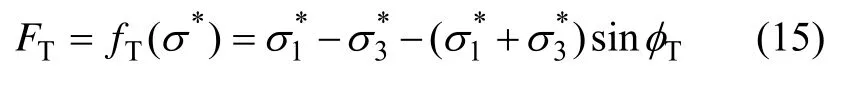
式(15)包含有效应力，因此，需要得到用名义应力表示的应力。根据式(4)可得：

由式(11)可得

将式(18)分别代入式(16)和式(17)可得：

将式(19)和式(20)代入式(15)则可得到基于Mohr- Coulomb 准则的高温作用后微元体应力：

1.3 统计热损伤本构模型

岩石内包含的裂隙和许多其他缺陷分布方向是随机的，因此，可以在计算方程中引入反映强度统计特点的函数[29]。KRAJCINOVIC等[30]将连续损伤理论和统计强度有机地结合起来，提出1 个统计损伤本构模型。唐春安[21]提出常温状态下岩石微元体强度符合Normal分布，本文假设高温作用后岩石微元体强度服从Normal分布，类比常温状态下概率密度函数[24]，在高温下，概率密度函数表示为

式中：FT为微元强度随机分布的应力；S0及Fn0为不同温度作用后Normal分布函数参数，它们反映岩石材料经历不同温度作用后的力学性质。

将式(22)代入式(2)可得

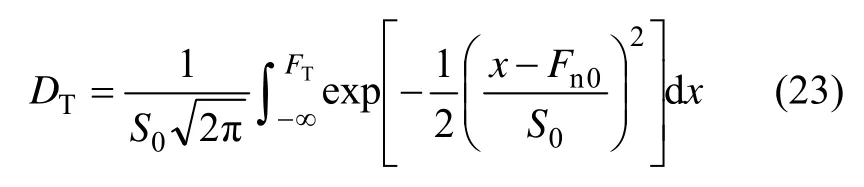
将式(23)代入式(11)，根据广义胡克定律，基于Normal分布下高温作用后岩石统计热损伤的本构方程则可表示为

2 参数确定

本文所提出的岩石统计热损伤模型涉及到的力学参数包括ET，vT，cT和Tφ，均可通过高温作用后岩石常规三轴试验测得。在不同温度下，Normal分布参数S0和Fn0可以依据LI等[25]提出的极值法确定，具体求解过程如下。

岩石于低围压条件下表现出屈服特征，应力达到峰值后随应变的增加而降低。因此，对应峰值点的导数等于0，即

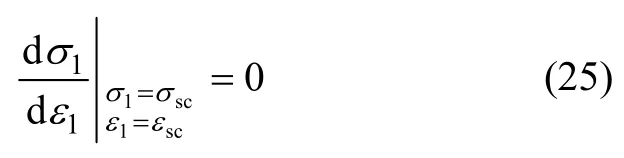
式中：scσ和scε分别表示峰值应力及相对应的峰值应变。将峰值点坐标(scσ，scε)代入式(21)和式(24)，可得

式中：Fsc为且时的岩石微元体强度。由式(19)，(20)和(24)可得出

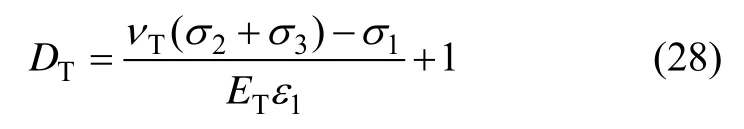
结合式(23)和(26)，DT可以表示为

式中：Dsc为且时的热损伤变量；Fsc如式(26)所示。

结合式(26)，(27)和(30)，式(25)可以表示成

假设式(30)中Z=(Fsc-Fn0)/S0，Z可查看标准正态分布表获得，因此，结合式(30)和式(31)，不同高温作用后S0可表示为

同时，不同温度作用后Fn0可表示为

3 模型验证与讨论

本文引用秦严[31]通过高温后花岗岩单轴和三轴压缩试验的相关研究成果，以验证本文所提出的岩石统计热损伤本构模型的合理性及适用性。

在此项研究中，岩样常温下纵波波速为4 800 m/s，完整性和均匀性较好，平均密度为2.72 g/cm3，平均单轴抗压强度为83.33 MPa，泊松比为0.141，内摩擦角为48.38°，黏聚力为19.81 MPa。X 线衍射分析其矿物成分的质量分数为：石英42%，斜长石39%，微斜长石14%，云母5%。在试验过程中，高温处置的升温速率为3℃/min，目标温度为100，200，300，400和500℃，岩样温度达到目标温度后恒温2 h，再在高温炉内自然冷却，三轴试验的围压为5，15和25 MPa。各个温度和围压作用下试验样本数均为3 个。

根据秦严[31]的试验结果，本文所建模型参数取值如表1所示。表1 中，各温度和围压作用下Normal分布参数S0和Fn0通过式(32)和式(33)得出。由式(24)可得不同温度和不同围压作用下岩石应力-应变关系的理论曲线，见图2。从图2可以看出：在同一围压下，花岗岩抗压强度和弹性模量随温度升高逐渐降低，说明高温作用后花岗岩力学性质发生劣化，高温对岩石具有损伤作用，岩石的峰值应变随温度增大而增大；应力-应变曲线随温度增大而向右移动，表明随温度的增大岩石塑性变形增大；不同温度作用后，花岗岩抗压强度和弹性模量随围压升高而增大，围压具有提高岩石强度的作用。通过对比试验数据与理论曲线可知：试验结果与理论结果拟合程度较好，理论结果可以反映花岗岩强度和变形随温度和围压变化的趋势，表明本文提出的考虑温度效应的统计热损伤本构模型能够较充分地反映岩石峰后软化特征和岩石强度依赖于温压状态的特征，同时能更好地表征不同温度和不同围压条件下岩石应力-应变曲线全过程，且围压越高，吻合程度越高。

在求解方法上，本文依据岩石屈服概念，利用极值法确定模型参数。此确定方法适用于不同温度和围压作用下加载试验数据的求解，不包含非常规岩石力学参数，工程应用更加方便。在岩石统计热损伤模型建立过程中，模型所用力学参数和统计分布参数与岩性无关，故本模型同样适用于其他不同岩性的岩石。

表1 不同温度下损伤岩石的模型计算参数Table 1 Model parameters of thermally treated rocks in different temperatures

值得注意的是：在进行单轴试验时，岩石应力-应变曲线通常存在原生裂隙和孔隙的压密阶段，表现 出明显的非线性特征；本文所提出的岩石统计热损伤本构模型是基于广义胡克定律建立的，认为岩石受压后即进入弹性阶段，忽略了岩石原生裂隙、孔隙及受热损伤所产生微裂隙闭合的影响，因此，在单轴压缩条件下，理论曲线和试验数据之间存在一定偏差，偏差在合理的范围内，这与徐银花等[19]由所建立的单轴压缩条下模型所得结果及试验结果一致。进行三轴压缩试验时，在围压作用下，岩石中的微裂隙和孔隙发生闭合，应力-应变曲线压密阶段不明显，且随着围压升高，应力-应变曲线起始阶段越呈现线性特征，所以，理论曲线与三轴压缩试验曲线较吻合。

图2 不同温度下试验和理论曲线的对比Fig.2 Comparison between calculated and experimental curves after thermal treatment at different temperatures

4 结论

1)本文所建立的本构模型能够充分反映了岩石的峰后软化和残余强度特征，很好地描述了不同温度和压力下全应力-应变曲线，围压越高，吻合程度越高。

2)本文模型所需参数均可根据高温岩石单轴和三轴压缩试验结果确定，不包含非常规岩石力学参数，工程应用方便，并且与岩性无关，具有适用性广的特点。

3)模型忽略了岩石原生裂隙、孔隙及受热损伤所产生微裂隙的影响。在单轴压缩条件下，理论结果和单轴压缩试验结果存在一定偏差；在三轴压缩条件 下，随着围压升高，岩石原生裂隙和孔隙及热损伤所产生的微裂隙逐渐被压实，理论结果与常规试验结果较吻合。