压缩载荷下织构对冷轧和退火Cu板力学行为各向异性的影响

王仁可，陈志永，邵建波，肖柱，刘楚明，唐建国

(中南大学 材料科学与工程学院，湖南 长沙，410083)

对高速冲击下金属材料动态行为进行研究对于金属材料在国防和工业中应用具有重要的意义。军事上的穿甲、爆破和工业上的高速切削、爆炸成型等均与材料在冲击载荷、高应变率下的响应密切相关，为此，必须深入研究材料在高应变率下的动态行为。由于Cu具有良好的塑性，其已经成为高应变率下研究较多的材料[1-5]。MEYERS等[6]发现具有不同晶粒尺寸多晶Cu的动态力学行为与准静态时的类似；NEMAT- NASSER等[7]基于位错动力学和热力学预测了多晶Cu的流变应力；ALEXANDER等[8]发现初始各向同性的纯铜在等径角挤压后会出现力学行为的各向异性；LI等[9-10]研究了低温动态塑性变形条件下Cu的微观结构演变以及退火对纳米铜动态力学性能的影响，认为高密度的变形孪生在纳米晶形成过程中具有重要作用，并认为退火后纳米铜的强度与延性均比应变诱导的超细晶铜的高。MISHRA等[11]研究了动态加载条件下等径角挤压铜的力学行为，但没有考虑材料的各向异性。陈志永等[12]研究了冷轧Cu 板法向、轧向和横向等轧制样品在这3 个特征方向的动态压缩力学行为各向异性，但对退火Cu 板展现出来的近似各向同性未进行深入研究，没有分析织构对其行为的影响。TANG等[13-14]研究了动态变形中不同应变条件下退火Cu 板剪切带内微观结构的演化。MA等[15]研究了锌含量对铜-锌合金静态及动态力学性能的影响。MAO等[16]分别在低/高应变速率下研究了铜应变速率敏感性与晶粒粒度的关系。作为制备铜药型罩所需的重要原材料，初始Cu 板板平面各方向上力学行为的差异即各向异性对其破甲性能具有重要影响，其实质是织构对射流的形成和稳定性的影响。理想药型罩应具有高密度和足够的动态延性，且其力学行为具有近似各向同性。因此，研究织构对Cu 板力学行为各向异性的影响有重要意义，且具有重要的实际应用价值。为此，本文作者利用 Instron 电子拉伸机和分离式Hopkinson 压杆等实验装置，研究准静态和动态压缩条件下织构多晶冷轧和退火Cu 板板平面力学行为各向异性特征规律，考虑晶体学取向分布即织构并基于微观晶体塑性理论，探讨织构对其力学行为各向异性的影响规律，以期为金属材料动态力学行为的研究以及高性能破甲弹的研制提供参考。

1 实验

以工业纯Cu为原料，原始状态为锻态，初始厚度为60 mm，冷轧变形总压下量90%至6 mm，截取部分冷轧板材在450℃退火2 h。对冷轧和退火Cu板分别沿与板材轧向成0°，45°和90°方向取圆柱形试样(样品编号分别为RD-0°，RD-45°和RD-90°)，其长度和直径均为5 m，然后，在Instron 电子拉伸机和分离式霍普金生压杆(split hopkinson pressure bar,SHPB)实验装置上进行准静态(应变率约为1×10-3s-1)和动态(应变率约为4×10-3s-1)压缩实验，并获得不同方向上的准静态和动态压缩应力-应变曲线。采用全自动X线衍射仪测量样品{111}，{220}，{200}和{113}不完整极图，应用BUNGE[17]球函数谐分析法及LÜCKE[18]高斯函数织构组分拟合方法计算相应的取向分布函数ODF(orientation distribution function，最大展开项级数lmax=3，包括偶数项和奇数项展开系数)。

2 结果

2.1 退火Cu 板织构

图1所示为冷轧变形和相应退火后Cu 板的真ODF图。从图1(a)可以看出：冷轧Cu 板取向分布具有轧制变形织构基本特征，主要聚集在取向空间α和β 线附近；α 线上主要有高斯取向G{110}〈001〉(0°，45°，0°)和黄铜取向B{110}〈112〉(35°，45°，0°)，在此取向线上所有取向的{110}面平行于板平面；β 线由铜取向 C{112}〈111〉(90°，35°，45°)经由S{123}〈634〉(61°，34°，64°)(具体位置略有变动)与α 线相交于黄铜取向B。图1(b)所示为退火Cu 板的真ODF，从图1(b)可以看出其同时具有轧制变形织构和再结晶退火织构特征，轧制织构主要为C 织构，再结晶织构主要为立方织构，可见在此情况下其再结晶过程尚未充分完成。

图1 冷轧和退火Cu 板的真ODF图Fig.1 True ODFs for cold-rolled and annealed copper sheets

2.2 织构多晶体板材压缩力学行为各向异性

图2所示为冷轧织构多晶Cu 板各方向的压缩真应力－真应变曲线。在加载过程中，各个试样都经历了明显的弹性变形与塑性变形阶段。从图2(a)可见：在准静态压缩变形时，RD-90°样品的屈服强度和流变应力最大，RD-45°样品次之，RD-0°样品最小；在高应变较高时，各样品的流变应力变化趋势趋于一致。从图2(b)可见：动态压缩变形时，依然是RD-90°样品屈服强度和流变应力最大，RD-45°样品次之，RD-0°样品最小。以上结果表明无论是准静态还是动态压缩变形，冷轧织构多晶Cu 板的力学行为均具有明显的各向异性，且变化规律一致，在动态加载下，各向异性更加显著。图3所示为退火Cu 板不同方向上的准静态压缩应力-应变曲线。从图3可见：不同方向上的屈服强度以及在真应变低于0.2 时的流变应力基本一致，力学行为近似各向同性；当真应变高于0.2 时，各方向上的流变应力略微有所差别。尽管准静态下退火Cu 板压缩力学行为表现出的各向异性程度很小，但织构分析表明退火Cu 板的晶体取向分布表现出一定程度的择优取向，故需分析织构对冷轧和退火板材平面不同方向的压缩力学行为的影响规律。

图2 冷轧Cu 板准静态和动态压缩真应力-真应变曲线Fig.2 Compress true stress-strain curves of samples with different directions for cold-rolled copper sheet

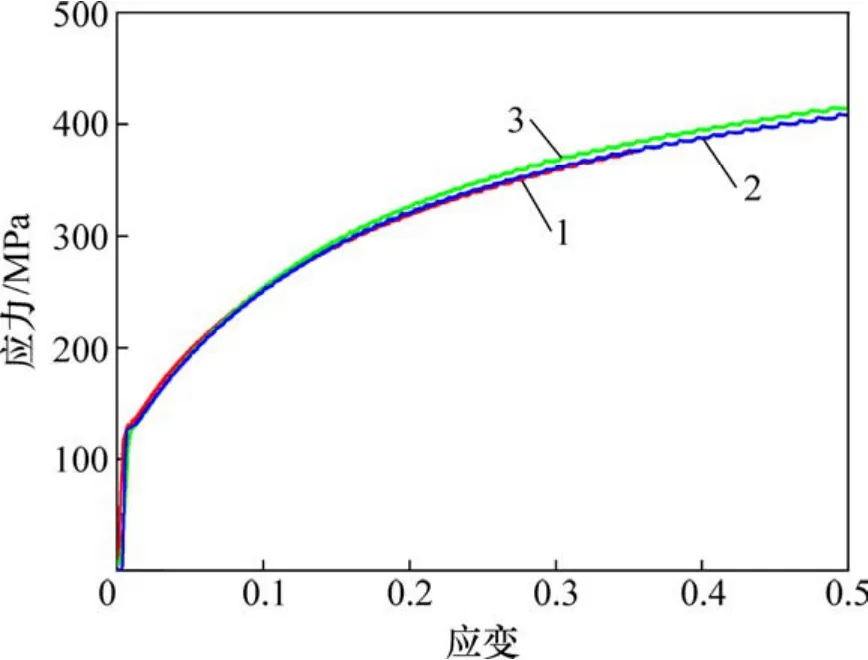
图3 退火Cu 板准静态压缩(应变率约为1×10-3 s-1)真应力-应变曲线Fig.3 Quasi-static compressive(ε˙is about 1×10-3 s-1)true stress-strain curves of samples with different directions for annealed copper sheet

3 分析与讨论

冷轧Cu 板织构较强，其力学行为表现出各向异性。退火Cu 板尽管织构较弱，但依然表现出一定的择优分布，其力学行为近似为各向同性，故难以依据多晶体板材内是否存在织构来判断其是否存在各向异性。当多晶体内具有织构时，其宏观性质受到相应单晶体的各向异性以及晶粒取向分布这2 个因素的双重影响，在此情况下，材料的宏观行为可以表示为晶粒微观行为的总和。基于此，对于具有初始织构的样品，首先将初始样品离散化，即将其表示为一些具有特定权重分立取向的组合。图4所示为离散化后，由具有特定权重分立取向计算的取向分布函数(ODF)，与实测ODF(见图1)相比，离散化后的晶体取向保持了冷轧和退火Cu 板织构的基本特征，可作为其各向异性分析的出发点。

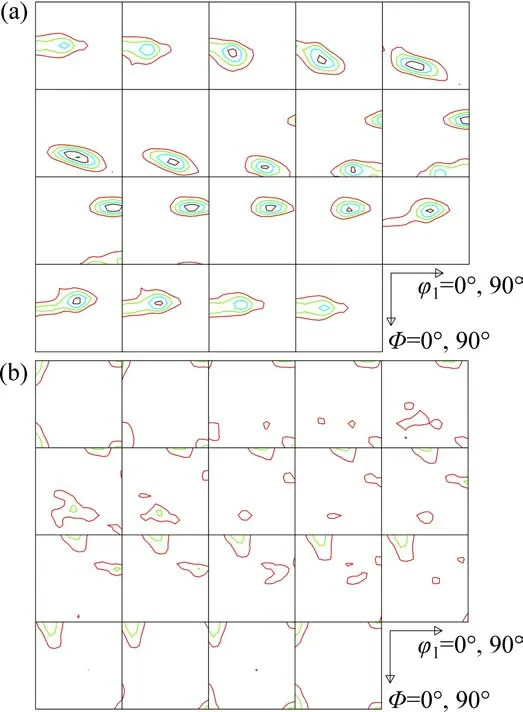
图4 冷轧和退火Cu 板的离散化后的真ODFFig.4 True ODFs calculated from individual orientations for cold-rolled and annealed copper sheets

一般地，当单晶体的塑性行为确定后，金属多晶体的塑性行为依赖于微观物理量向宏观物理量转换，因此，考虑单个晶粒变形机制的多晶塑性理论时必须将它们联系起来。根据塑性变形条件，人们提出了多种多晶体变形模型，主要分为 SACHS[19]和TAYLOR[20]模型以及由此而产生的各种修正模型。对于fcc 金属，由于Taylor 模型比Sachs 模型更能反映实际结果，因此，本文采用Taylor 模型分析其压缩行为各向异性。

为便于分析织构多晶板材不同方向上的力学行为，采用R，S和C分别表示轧制(RD，TD，ND)、样品压缩(X，Y，Z)和晶体(〈100〉，〈010〉，〈001〉)的坐标系。Taylor 模型假定多晶聚集体内各晶粒所承受的应变与宏观应变一致。对于多晶聚集体压缩塑性变形，它可由X方向上的压缩变形以及Y和Z方向上的延伸变形来描述，应变张量可表示为

式中：上标S表示样品压缩坐标系。设α为压缩方向(X)相对于轧向(R)的夹角，即样品压缩坐标系相对于轧制坐标系的夹角，则轧制坐标系相对于样品压缩坐标系的取向矩阵为

依据张量转换法则：

可将样品压缩坐标系上的应变张量转换到轧制坐标系。假定晶体坐标系相对于轧制坐标系的取向矩阵为g，则有

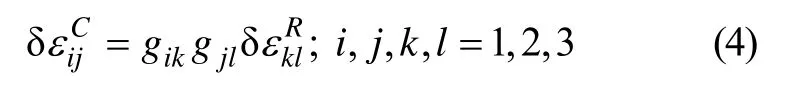
其中：

从轧制坐标系出发，将晶体坐标系按φ1，φ和φ2顺序转动，即可得到欧拉空间的任一取向(φ1，φ，φ2)。对于任意取向的晶粒，将BISHOP-HILL[21-22]最大塑性功原理拓展于滑移或/和孪生共生变形之中，根据

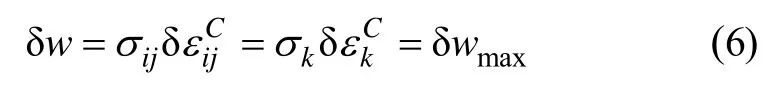
可以确定实际所需的屈服应力(包括滑移或/和孪生屈服应力)，由此也可确定相应启动的滑移或/和孪生系。定义Taylor 因子为

其中：csτ为{111}〈110〉滑移临界剪切应力。在此基础上，进一步考虑晶体取向分布，将上述过程应用于具有一定初始织构的样品的离散化取向，再根据各自的权重Vi加权计算总的Taylor 因子，即

显然，可以将任一取向的Taylor 因子作为相对强度的度量：Taylor 因子越大，使材料产生塑性变形所需外力越大。

由于Cu为中等层错能金属，在室温准静态变形条件下变形机制一般为{111}〈110〉滑移；在冲击载荷即本文实验条件下，{111}〈110〉滑移和{111}〈112〉孪生机制可能同时发生作用。CHEN等[23]对fcc 晶体引入孪生机制，将滑移和孪生综合起来进行考虑，系统分析了当{111}〈112〉孪生对{111}〈110〉滑移的临界分解剪切应力之比ξ不同时，fcc 晶体滑移和/或孪生共生单晶共生屈服应力状态及其特征，发现：当时，仅能产生滑移，有56 种应力状态；当时，仅能产生孪生，有25 种应力状态；只有当时，滑移和孪生才可能同时产生，且仅存在2种类型混合屈服面，其临界值为，共有259种应力状态，其中139 种相同，120 种不同。在此基础上，根据各种多晶体塑性变形模型，结合织构离散化后冷轧和退火Cu 板具有一定权重的分立取向，可以计算不同塑性变形机制起作用下的织构多晶板材的Taylor 因子，分析其压缩行为各向异性。

图5所示为仅考虑{110}〈111〉滑移变形机制时，采用上述方法计算的冷轧和退火织构Cu 板平面内不同方向的Taylor 因子。计算时考虑了样品对称性，即对于某一取向g1(φ1，φ，φ2)，有3 个对称取向g2(180°+φ1，φ，φ2)，g3(180°-φ1，180°-φ，φ2)和g3(360°-φ1，180°-φ，φ2)。很明显，对于冷轧织构多晶Cu 板，其不同方向上的Taylor 因子差异较大：随着轧制方向角度增大，其Taylor 因子先减小，在33°方向附近其Taylor 因子最小，然后，随着与轧制方向角度的增大而进一步增大，在RD-90°方向上的Taylor 因子达到最大，表现出强烈的各向异性，且Taylor 因子相对于RD-90°方向对称。对于退火织构多晶Cu 板，其Taylor 因子变化非常平缓，与初始织构为自由取向分布的各方向的Taylor 因子相差不大，近似为各向同性，说明尽管退火Cu 板晶体取向择优分布具有初始织构，但由于其再结晶织构和形变织构达到了较好平衡，其宏观压缩力学性质表现出近似各向同性。

图6所示为考虑{110}〈111〉滑移和/或{112}〈111〉孪生变形机制时和共4 种情况)计算的冷轧和退火织构Cu 板板平面内不同方向的Taylor 因子。需指出的是：随着ξ减小，其Taylor 因子均降低，这并不意味着使金属产生塑性变形的外力越来越低。这是因为随着应变率增加，由于Cu为应变速率正敏感性材料，其滑移和孪生的临界分解剪切应力也随之增大，导致其产生塑性变形的外力也相应增大。显然，对于冷轧织构多晶Cu 板，随着ξ减小即塑性变形机制由滑移向滑移和/或孪生塑性变形机制转变，其Taylor 因子的变化规律是相似的，均表现出各向异性，且各向异性程度越来越低。对于退火织构多晶Cu 板，不管其塑性变形机制如何变化，其Taylor 因子变化较平缓，近似为各向同性。将Taylor 因子归一化，也可得到同样结论。

图5 仅考虑{110}〈111〉滑移时冷轧和退火Cu 板Taylor 因子Fig.5 Taylor-factors of cold-rolled and annealed Cu sheet considering{110}〈111〉slip

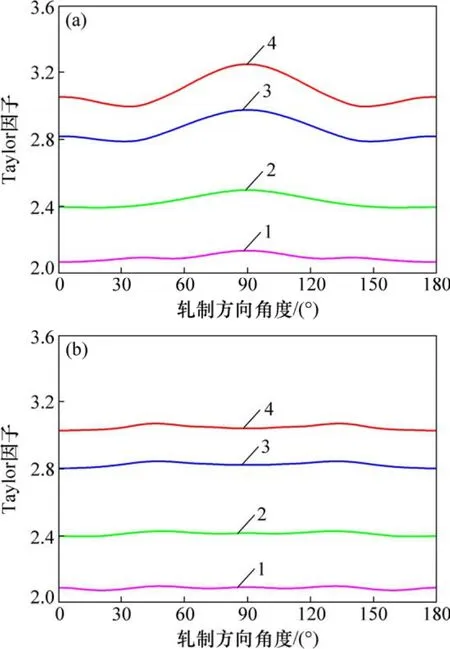
图6 考虑{110}〈111〉滑移和/或{112}＜111〉孪生时 Cu 板的Taylor 因子Fig.6 Taylor-factors of Cu sheets for{110}〈111〉slip and/or{112}〈111〉twinning

由上述分析可知：无论是准静态还是动态压缩变形，对于冷轧和退火织构Cu 板，考虑晶体取向分布即织构的影响，其各向异性规律与实验结果定性符合，可见本文分析结果与实际结果基本相符。

4 结论

1)退火织构多晶Cu 板3 个方向上的力学行为差别很小，近似为各向同性；相比较而言，冷轧织构多晶Cu 板准静态和动态压缩力学行为呈现出明显的各向异性，RD-90°方向屈服强度和流变应力最大，RD-45°方向的次之，RD-0°方向的最小。

2)考虑晶体取向分布即织构的影响，计算了板平面内与轧制方向成不同角度样品方向导致压缩塑性变形所需外力强度因子，结果可用于定性解释织构多晶Cu 板压缩力学行为各向异性。退火Cu 板表现出近似各向同性的原因是其再结晶织构和形变织构共同作用即两者之间相互平衡。