基于改进TOPSIS方法的坦克分队作战方案优选*

张 昭，宋跃进，武富春，王 明*，董棋宁

（1.北方自动控制技术研究所，太原 030006；2.中国兵器科学研究院，北京 100081）

0 引言

坦克分队作战方案优选是作战分队根据收到的上级任务，对多组作战行动方案进行评估、排序和选择的过程［1］。由于作战方案的提出和评估优选都是在作战分队层面，方案总数较少，而且较为具体。评估过程中需要考虑作战效果、作战时间、损失情况等因素。这一问题最终可以抽象为少量方案条件下的多属性对象排序问题［2］。

在作战方案评估优选问题的方法选择上，张道延等采用了层次分析法和效用模型的方法［3］。田福平等采用了模糊综合评判与作战模拟的方法［4］。刘飞等采用了博弈理论方法［5］。徐大杰等采用了传统的TOPSIS方法［1］。此外还有层次分析法、兰彻斯特方程法等常用方法［6］。与其他方法相比，TOPSIS方法具有计算较为简单，不过分依赖主观经验，充分利用数据，信息损失少等优点。

本文采用了改进的TOPSIS方法对作战方案进行评估优选，对传统TOPSIS方法在处理少量方案问题上的不足作出了改进。

1 TOPSIS方法

TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）方法，也称为逼近理想解排序方法，是Hwang等人在1981年提出的一种针对多属性对象的评价排序方法［7］。其算法核心是设定正理想解和负理想解，计算各个对象到正、负理想解的欧式距离进而得到各个对象的相对优劣程度［8］。其中，“正理想解是设想的最好的解，它表示各个单一属性值都达到了方案集中的最优值；而负理想解则是设想的最差的解，它表示各个单一属性值都达到了方案集中的最差值”。

TOPSIS方法给出了从各个评价对象中得到正、负理想解的方法，从而解决了设定正、负理想解的问题。但是采用这种方法得到的只是用各个评价方案的数据拼凑出的最优和最差解，并不是真正意义上的“理想”解。若存在大量评价对象，以上两者可以近似，但在评价少量对象时，这种选取正、负理想解的方式并不合理。此外传统TOPSIS方法还存在逆序问题。所谓逆序问题是指在对m个方案作评估排序时，方案Ai优于方案Aj（i≠j），但若增加或减少若干个方案后，相同方法得出的结论却是方案Aj优于方案Ai（如果这两个方案没有被删减）［9］。

1.1 TOPSIS方法原理和具体步骤

TOPSIS方法的具体应用步骤如下［10-13］：

Step 1：由待评价对象构建如下评价矩阵X：

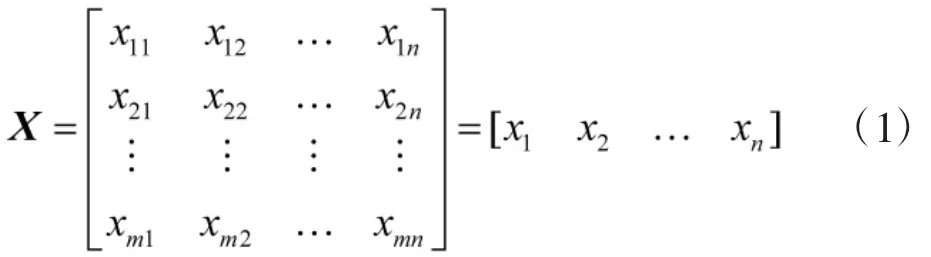
其中，xij是第i个评价对象的第j个属性指标的值。m、n分别为评价对象和评价指标的数量。xj是m个评价对象的第j个属性指标构成的向量。

Step2：为了消除量纲和数量级的影响，对原始评价矩阵X进行归一化处理，得到归一化后的矩阵R：

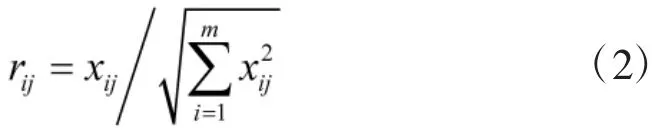
其中，式（2）为归一化处理公式。rij是归一化之后的第i个评价对象的第j个属性指标的值。

Step 3：将权重矩阵W右乘归一化后的矩阵R得到价值矩阵V：

其中，权重 ωi满足 ωi>0，且。

Step 4：确定正理想解S+和负理想解S-。正、负理想解是TOPSIS方法给出的设想中的“最优”和“最差”的解。具体方法是让正、负理想解的各个指标分别取评价矩阵中的对应指标中的最优和最差指标的值。指标分为效益型指标和成本型指标，其中效益型指标的指标值越大效果越好，成本型指标的指标值越小效果越好［7］。

Step 5：分别计算每个评价对象到正、负理想解的距离 Di+、Di-。

Step 6：计算各评价方案相对贴近度Ci*：

Step 7：根据Ci*的大小进行排序，值越大，评价方案越好。

1.2 TOPSIS方法在针对少量对象评价中的不足

TOPSIS方法的核心思想是利用待评价对象到正、负理想解的距离来衡量待评价对象的优劣。距离正理想解越近且距离负理想解越远的待评价对象越好，反之则越差。TOPSIS方法给出的正、负理想解的求取方法，是取评价矩阵中每个指标的最优和最差值作为正、负理想解对应指标值。这种选定正、负理想解的方法可以从评价对象直接得到，不需要通过其他方法获得。

在评价排序问题的对象数量较多时，可以近似认为评价矩阵中的各个对象可以覆盖评价方案的取值空间，TOPSIS方法给出的正、负理想解，近似于整个取值空间中各个单项指标的最优、最差指标值组成的最优、最差解。

但是在评价矩阵中对象较少的情况下，矩阵中的各个对象并不能近似遍布评价方案的取值空间。TOPSIS方法给出的正、负理想解并不能代表整个取值空间中每个单项指标的最优、最差指标值组成的最优、最差解，只是评价矩阵中的指标组成的最优和最差解，作为评价标准可能存在一定误差。

此外TOPSIS方法还存在逆序问题。在评价标准不变的情况下，由于评价方案数目的增减导致原本的方案评价排序发生变化，显然是不合理的。虽然在对作战方案进行评估的过程中，一般不会出现增减方案的情况，但这种逆序问题的存在说明传统的选取正、负理想解并作为评价标准的方法有一定瑕疵［14-16］。

具体例子将在第3节实例分析中给出。由于存在以上问题，在评价矩阵中对象较少的情况下，不应该采用传统的选取正、负理想解的方法。

2 针对少量评价排序对象的改进TOPSIS方法

在面对少量对象的评价排序时，针对TOPSIS方法的不足，本文提出将评价方案的取值空间中各指标的边界值作为正、负理想解的各指标值。这些边界值可以是数学上的边界值，例如对敌毁伤概率的上边界为1；可以由任务要求得到，例如任务要求在60 min内完成任务；也可以由评价排序方自行根据实际情况制定，例如进行TOPSIS方法评价排序时要求毁伤概率不得低于0.8。

原本的TOPSIS方法中，正、负理想解是在原始评价矩阵经过变换之后，再取各个指标的最大、最小值得到的。人工设定正、负理想解时，不宜直接给定与变换之后的评价矩阵相对应的正、负理想解。因此，针对原始评价矩阵中各个指标给定最好和最差的解，再跟随原始矩阵一起变换得到最终的正、负理想解。给定过程中应考虑效益型指标和成本型指标的不同来选择最大或最小。对TOPSIS方法做出的具体修改如下。

构建原始正、负理想解。通过评价方案的取值空间的边界、任务要求和经验补充等构建对应原始矩阵的最优、最差解。并将这两个解加入原始评价矩阵X，得到新的评价矩阵X'。

对评价矩阵X'的前m行进行归一化处理，对x1、x2做对应处理，得到矩阵 R'：

其中，式（11）为原归一化处理公式变化之后的公式，式中的 i=1，2，3，…，m+2，j=1，2，3，…，n。但求和公式中i最大取m。因此，该公式不会影响原始评价矩阵X中的各个元素的归一化结果，同时对增加的原始正、负理想解做出对应的变化。式（12）为变换之后的矩阵。

用R'代替原本TOPSIS方法中的R与权重矩阵进行加权，得到改进后的价值矩阵V'，其中最后两行即为改进后的正、负理想解。

3 算例分析

下面以文献［1］中的实例数据作为例子进行简要计算分析：

某坦克分队要对某阵地防御发起进攻。要对现有的4个方案进行评估排序，每个方案有对敌毁伤概率、完成作战任务时间、遭敌毁伤概率、弹药消耗量4个评价指标。原始数据如表1所示。

表1 4种作战方案的原始数据

原始数据中，对敌毁伤概率为增益型指标，越大越好；完成作战任务时间、遭敌毁伤概率、弹药消耗量属于成本型指标，越小越好。

原始评价排序矩阵为：

3.1 TOPSIS方法在针对少量对象时的算例分析

表2 4种作战方案按传统方法的评价排序结果

首先按照传统的TOPSIS方法对以上作战方案进行评价排序，其中权重选择采取传统的信息熵的方法，计算得到4种作战方案在传统TOPSIS方法下评价排序结果。

在上述计算过程中，正、负理想解由原始评价矩阵中每个指标对应的最优和最差指标值通过变换得到。现设定 x1=（0.99 32 0.5 200）、x2=（0.80 100 1.0 1 200）分别作为原始的最优和最差方案，与原始评价矩阵中的4个方案经过相同的变换之后作为修改后的正、负理想解。4种作战方案在修改正、负理想解之后的评价排序结果如表3所示。

表3 4种作战方案在修改理想解后的评价排序结果

对比修改正、负理想解前后的排序结果可以发现：在修改正、负理想解之后，方案排名出现了变化。修改前D方案最优，C方案其次；修改后C方案最优，D方案其次。

上述修改过程可以认为是人工设置的正、负理想解。若令上述修改过程中，式（11）中的求和公式i最大取m+2，则可以认为是在原本的4个方案基础上增加了两个特殊方案。在此种情况下，原来4个方案的排序为C、D、A、B，验证了逆序问题的存在。具体计算过程不再赘述。

这样的排序变化验证了在评价矩阵中对象较少的情况下：TOPSIS方法使用原本的正、负理想解和人工按照边界设定的正、负理想解可能会得到不同的评价方案排序结果；传统的TOPSIS方法存在逆序问题。

因此，在评价矩阵中对象较少的情况下，TOPSIS方法的正、负理想解的选定方法有着明显的不足。

3.2 改进TOPSIS方法算例分析

现将原始的最优和最差方案x1、x2加入评价矩阵得到新的评价矩阵X'如下：

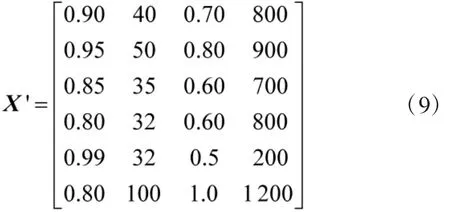
对原始数据归一化，并对x1、x2作对应处理之后得到R'如下：

按照各项指标的重要性给定权重W=（0.4，0.3，0.2，0.1）。得到价值矩阵V'如下：

根据相对贴近度给出的4个方案的排序为C、D、A、B。

4 结论

针对坦克分队的方案优选问题，本文分析了传统的TOPSIS方法在面对少量对象的评价排序时的不足：排序方案较少时，以传统方法选取的正、负理想解合理性不强；传统TOPSIS方法存在逆序问题。针对此种情况下的正、负理想解的选取，本文提出将评价方案的取值空间中各指标的边界值作为正、负理想解的各指标值的改进方法，并对传统的TOPSIS方法的计算步骤作出了相应的改进，使之更适于处理坦克分队的方案优选问题。

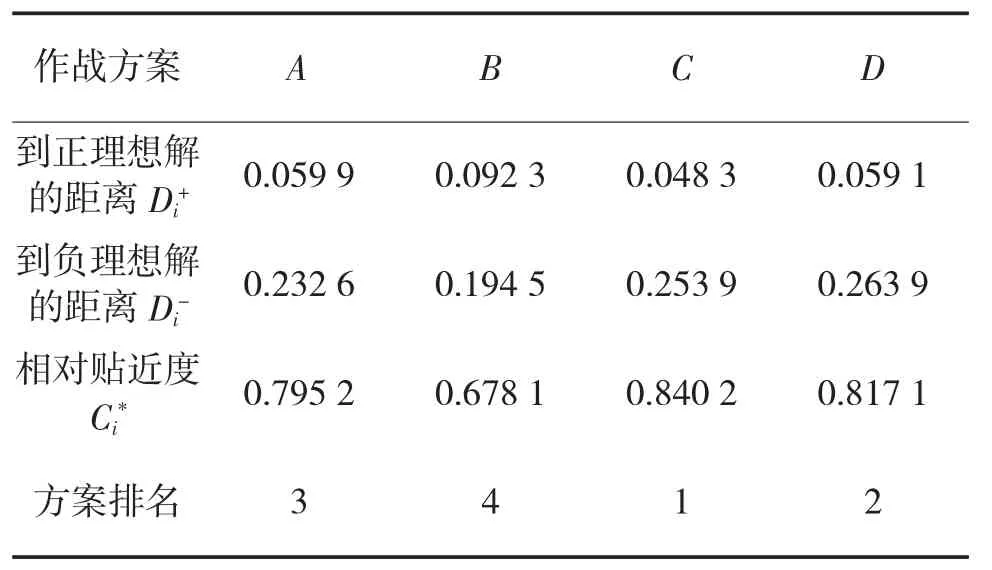
表4 4种作战方案按照改进TOPSIS方法的评价排序结果