温州深厚软黏土流变模型识别及工程应用分析

2019-07-18刘勇

铁道建筑技术 2019年4期

刘勇

（中铁第四勘察设计院集团有限公司湖北武汉 430063）

1 引言

温州市域铁路S1线总体为东西走向，西起沿海铁路温州南站南端潘桥镇，东至灵昆半岛，远期至洞头县洞头岛。是构建未来温州大都市核心区两大中心——中心城和瓯江口新城的快速联系通道。拟建工程经过区域多属于冲海积平原区。冲海积平原区土体厚度大，普遍发育淤泥、淤泥质黏土等特殊性软土。这些软黏土呈厚层状大面积分布，层厚一般为20～60 m，具有天然含水量高、渗透系数低、排水缓慢、固结时间长、易触变性、高压缩性、强度低等特点，工程性质差，运营隧道会产生长期沉降和不均匀沉降问题，甚至引发安全事故。因此，温州深厚软土流变问题成为温州市域铁路运营中的关键问题之一［1-2］。

对于软黏土流变特性本构模型的研究，早期主要是将固结模型与流变模型并联或串联后建立的组合模型为主［3-9］。后来各类新的模型不断出现，如根据黏性土的试验成果提出基于等效时间线的弹黏塑固结模型［10-11］及考虑排水条件的蠕变模型［12］、通过扰动状态面模型（DSC）的多功能特征和三轴试验成果建立的固结状态下的土体蠕变模型［13］等等。本文对深厚软黏土流变特性引起运营隧道长期变形规律进行分析研究，在温州软黏土室内流变特性试验的基础上，建立了软黏土弹粘塑性本构模型研究。并将弹粘塑性本构模型应用到铁路隧道中，重点分析了隧道运营期的流变效应。

2 考虑初始各向异性的非结构性软黏土弹粘塑性模型

2.1 模型的建立

根据Perzyna过应力理论，将土体总的应变率分为弹性应变率和粘塑性应变率：

其中弹性应变率与时间无关，并认为是各向同性的，可以采用修正剑桥模型的方法来描述：

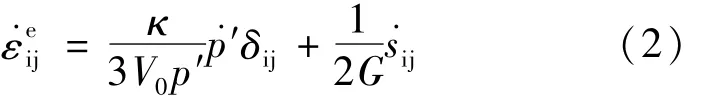
式中，κ为回弹指数；V0＝（1＋e0），为特征体积；G为剪切模量，与回弹指数κ和泊松比ν有关，G＝为平均有效应力；s˙为偏应力张ij量；δij为克罗内克符号。

根据Perzyna的过应力理论并结合流动法则粘塑性应变率可以表示为：

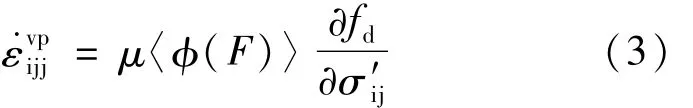
上式中μ是黏性参数；动态加载面fd被认为粘塑性势函数（相关联法则）；当F＞0时，［φ（F）］＝φ（F），当F≤0时，〈φ（F）〉＝0；在 Perzyna的过应力理论中φ（F）表示动态加载面与静态屈服面之间相对距离函数，即过应力函数，反映粘塑性应变率的大小，只有当应力状态位于静态屈服面以外时，才会发生粘塑性流动。

当处于超固结状态时，土体仍然会产生蠕变，说明当应力状态位于静态屈服面内部时依然会有粘塑性应变的产生。有必要对Perzyna的过应力理论中φ（F）进行修正。粘塑性应变率由动态加载面和参考面的相对距离函数（过应力函数φ（F））来反映，此处过应力函数φ（F）是动态加载面和参考面的相对距离的函数。不管动态加载面位于参考面的内部还是外部（对应于F≤0和F＞0），均会发生粘塑性流动，所以式（3）改写成：

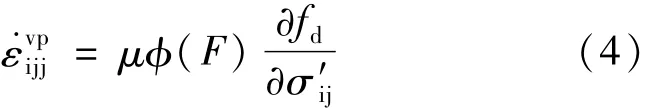
国内外对于K0固结状态的天然软黏土的屈服面的研究发现，由于初始各向异性导致软黏土屈服面是一个倾斜的椭圆，但是临界状态线在应力空间内的斜率仍为M。本文采用Wheeler的方法对动态加载面进行研究，用如下倾斜的椭圆来反映各向异性对动态加载面和参考面的影响：

上式中α表示动态加载面和参考面的倾斜程度，是各向异性变量，表征各向异性的强弱。α0是各向异性变量的初始值，反映初始各向异性的影响。当α0＝0时，上述屈服面退化为MCC模型的屈服面。当考虑各向异性随粘塑性应变发生演化时，α也随之发生变化。

上式中q表示偏应力大小；p′为平均有效应力；M为临界状态线的斜率为动态加载面与α轴交点在p′轴上的投影，表示动态加载面的大小为参考面与α轴交点在p′轴上的投影，表示参考面的大小；与修正剑桥模型类似，参考屈服面采用体积硬化准则：

动态加载面上任意一点的法向量在p′轴和q轴的投影分别为：

式中，η为有效应力比，η＝q／p′

根据式（4）并结合式（8）、（9）得到三轴应力条件下的粘塑性体积应变率和粘塑性偏应变率的表达式：

对于一维加载情况，η＝ηK0，α＝α0，则一维加载情况下的粘塑性体积应变率由式（10）得到：

将p′换成σ′v便可得到一维情况的体积粘塑性应变率：

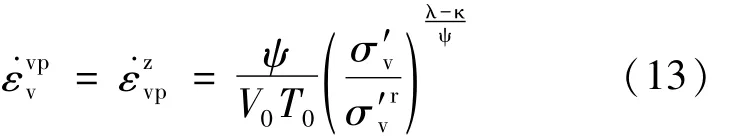
对比式（12）和式（14）可得到过应力函数的一种表达式：

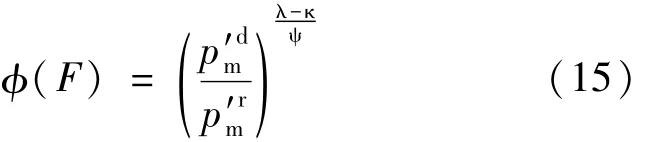
从过应力函数的表达式可以看出，任意动态加载面上过应力函数相等，与前文假设条件相符。联立式（1）、（2）、（4）、（5）、（7）、（15）只考虑初始各向异性软黏土三维弹粘塑性本构模型。

2.2 参数确定

从建立的理论模型可以看出，模型参数包括修正剑桥模型参数、初始各向异性参数、黏性参数。

（1）修正剑桥模型参数

修正剑桥模型参数包括回弹指数κ、压缩指数λ、泊松比ν、初始孔隙比e0、临界状态应力比M、初始参考面的大小κ、λ、e0可以通过一维压缩试验获得；M、ν可由三轴试验获得：M＝6sinφ′／（3-sinφ′）可以由一维参考前期固结应力确定如式（16）所示：

（2）初始各向异性参数

天然软黏土K0固结引起的初始各向异性可由以下方法定量确定。在三轴应力条件下，很容易求得：

忽略弹性偏应变得到：

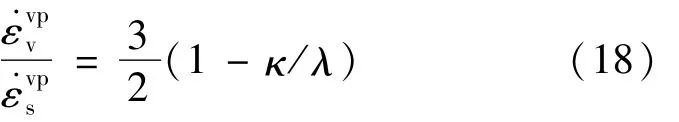
由式（10）、（11）得到：

上式中 ηK0＝3（1-K0）／（1＋2K0）。联立式（18）、（19）得到：

（3）黏性参数

联立式（12）、（14）、（15）可以得到黏性参数 μ的表达式：

3 温州深厚软黏土流变试验及模型验证

为了验证模型的正确性，本文通过加拿大Sackville地区黏土、温州、日本大阪三种软黏土进行K0固结三轴不排水剪切蠕变试验，通过得到的试验数据与模型进行对比对模型的适用性进行验证。

3.1 加拿大Sackville地区黏土蠕变试验与模型对比

选用加拿大Sackville地区黏土的K0固结三轴不排水蠕变试验来验证所建模型。试样首先在围压为56 kPa，K0＝0.76的条件下进行偏压固结，固结完成后进行如下试验：

试验1：在偏应力水平q＝35 kPa下不排水蠕变时间为8 000 min。

试验2：q＝44.5 kPa条件下不排水蠕变时间12 000 min后，当轴向应变和超孔隙水压基本稳定以后施加下一级荷载至q＝50 kPa，再继续不排水蠕变12 000 min。

图1为加拿大Sackville地区黏土在q＝35 kPa、q＝44.5 kPa、q＝50 kPa下轴向应变和超孔隙水压随时间发展的试验曲线和模拟曲线的对比图。从图可以看出随着偏应力水平的增大，剪应变的增长速度明显加快。除了q＝50 kPa，模型基本上能很好地描述轴向应变和超孔压随时间的发展规律。当q＝50 kPa时，计算得到的轴向蠕变由初始蠕变阶段进入稳定蠕变阶段的时间要比试验值小；计算轴向蠕变在试验后期已经进入加速蠕变阶段，而试验轴向应变并未进入蠕变破坏阶段，这也导致计算孔压和试验孔压逐渐出现偏差，即当计算的轴向蠕变开始进入加速蠕变阶段，孔压开始下降引起的。但是总体而言，本文模型能够很好地反映加拿大Sackville地区软黏土的蠕变特性。

图1 加拿大Sackville地区黏土三轴不排水蠕变的试验曲线和模拟曲线

3.2 温州黏土蠕变试验与模型对比

本文对温州10 m深的软黏土进行了不同围压下的等向固结三轴不排水蠕变试验。三轴不排水蠕变试验采用分级加载的方式，蠕变稳定标准规定为连续1 d内轴向变形量小于0.01 mm，则进入下一级偏应力水平下的三轴蠕变试验。现以围压为150 kPa的三轴不排水蠕变试验来验证本文模型的有效性，试验的偏应力级别分别为q＝37.27 kPa，q＝74.54 kPa，q＝111.8 kPa，q＝149.08 kPa，q＝194.94 kPa。

图2是计算得到的轴向应变随时间的变化曲线和试验曲线的对比。由图可以看出，在所选参数条件下模型能很好地反映温州10 m深软黏土等向固结三轴不排水蠕变试验不同偏应力下的轴向应变随时间的发展规律。模型不仅能有效地预测偏应力水平较低时的初始蠕变和稳定蠕变，而且还能准确地预测偏应力水平较高时出现的加速蠕变性状。

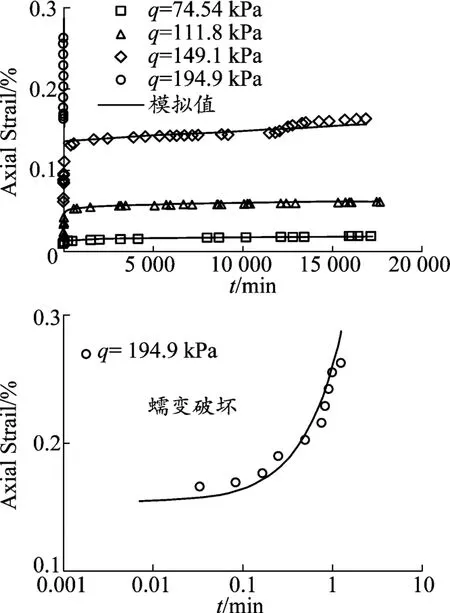
图2 温州10 m深软黏土等向固结三轴不排水蠕变试验曲线和计算曲线

3.3 日本大阪软黏土蠕变试验与模型对比

不排水剪切蠕变时，土体的应变和孔压的发展与土体偏应力水平密切相关，当偏应力过大时，土体在蠕变后期的应变率不仅不减小反而会持续增大，应变加速发展，出现剪切蠕变破坏，正如温州10 m深软黏土在q＝194.94 kPa时出现的蠕变性状。为了进一步验证模型能否成功模拟软黏土的蠕变破坏现象，针对日本大阪湾软黏土进行三轴不排水剪切蠕变破坏试验。图3分别为日本大阪湾软黏土在各种偏应力水平下不排水剪切蠕变过程中轴向应变和平均有效应力随时间变化的试验点与计算值比较。从图3a可以看出，当q／p′i≥0.663后，土样开始出现剪切蠕变破坏，轴向应变持续加速增长，而p′迅速减小至q／p′＝M为止。模型基本上能很好地描述蠕变破坏过程中的轴向蠕变应变随时间的发展规律。从图3b可以看出，模型对孔压的模拟效果不如对轴向应变的模拟，这主要与模型采用的弹性应变计算式及κ取值相关。但总体而言，本文模型较好地模拟发生蠕变破坏的破坏时间及轴向应变的加速发展，说明本文考虑土体黏性的思路是正确的。

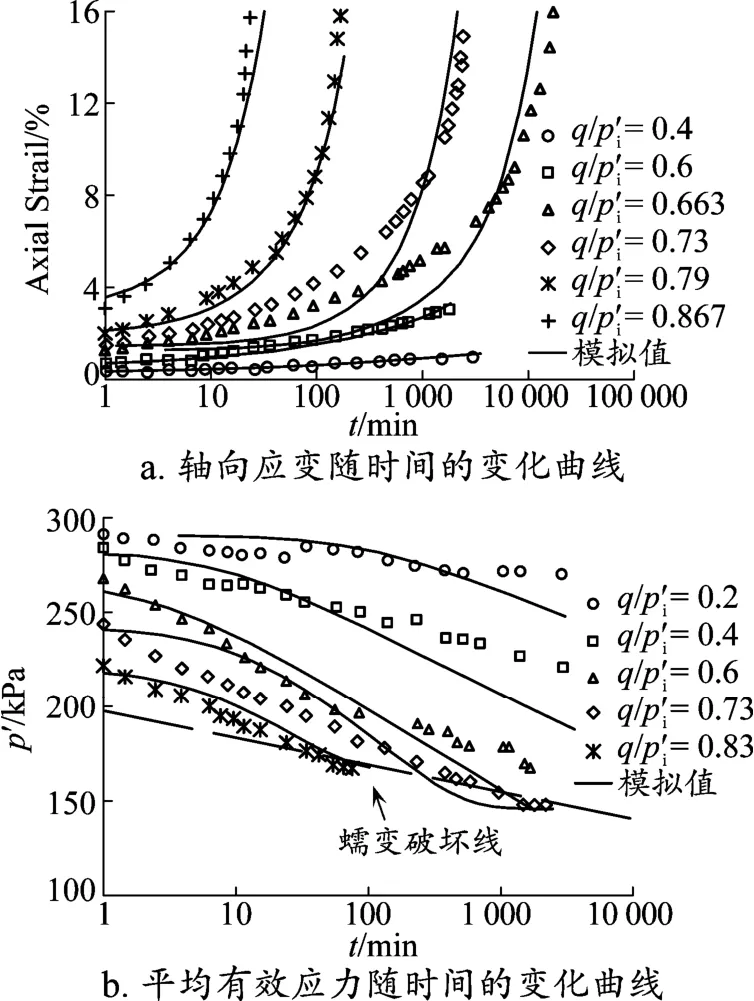
图3 日本大阪软黏土不排水蠕变破坏试验曲线及模拟曲线

4 工程应用

4.1 模型参数的选用

通过试验验证可以发现，该模型能够很好地模拟软黏土的蠕变规律。本文运用本模型对温州某区段的软黏土隧道的蠕变规律进行数值模拟。所采用的参数如表1所示。

表1 计算参数汇总

4.2 数值模拟

ABAQUS有限元分析软件在岩土工程计算中得到了广泛的应用。虽然ABAQUS自带丰富的土体本构模型，如剑桥模型、D-P模型等，但由于这些模型存在局限性，不能较全面准确地反映土体的特殊性质，如时效性、结构性、各向异性等。本文通过ABAQUS相应的用户材料子程序，通过UMAT子程序接口引入ABAQUS软件中，再利用ABAQUS强大的前、后处理和先进的数值模拟技术，对软土工程的长期变形和长期稳定性进行预测和模拟研究。

对软黏土盾构隧道长期变形的数值模拟采用二维平面应变计算模式，计算过程中采用不同的时间步和与其相应的工况来模拟隧道施工期、隧道运营期的变形发展规律。以温州城域铁路某盾构区间隧道为工程背景，模型的水平和竖直方向的长度均为60 m，隧道中心埋深20 m。数值计算中以隧道轴线为对称轴，其数值模型及单元划分如图4所示。土体单元类型为CPE4单元，其本构模型为采用本文建立的弹粘塑性模型。隧道衬砌采用三角形单元，其本构模型为弹性模型。在计算时假设管片拼装完成后，衬砌与土体始终保持接触状态且不会发生滑移，所以衬砌与土体之间的接触面采用绑定约束。

图4 数值模型及单元划分

本文主要考虑地铁运营期软黏土流变特性对隧道长期变形的影响，因此，对隧道复杂的施工过程进行简化处理。设置如下计算分析步：（1）设置初始地应力平衡；（2）对开挖区土体模量折减以达到应力释放的效果；（3）将开挖区的土体单元 “移除”并同时“添加”衬砌单元；（4）设置长期流变计算，根据地铁隧道的设计使用年限，流变计算时间为100年。由于隧道埋深较大，隧道施工引起的隧道周边的超孔隙水压难以消散，所以将地表作为不排水边界近似处理。位移边界条件为：地表不受约束、模型底面约束竖向位移、模型侧边竖向位移自由、约束横向位移。

4.3 结果分析

图5是地表沉降的分布规律，由图可以看出，由于软黏土存在很显著的流变特性，因此隧道施工引起的沉降槽会随时间逐渐发展，沉降槽随时间有整体下降的趋势，地表沉降也随时间逐渐增大。施工完成后100 d的隧道正上方地表沉降为42.48 mm，和施工完成时相比几乎没有变化。施工完成后1 000 d时隧道正上方地表沉降为44.56 mm，相对于施工期沉降增加了5.5%。施工完成10 000 d后的地表沉降最大值为54.93 mm，比施工期沉降增加了30%。隧道建成100年时隧道正上方地表沉降为74.67 mm，比施工期沉降增加了32.4 mm，增加了近76.7%。通过以上分析可知，软黏土流变特性引起的地铁隧道的长期沉降是很显著的。这对地铁的长期运营安全是一个极大的挑战，因此对隧道长期变形机理和控制措施的研究具有重要的工程意义。

图5 地表沉降时空分布规律

图6是距隧道轴线10 m处竖直测线L的水平位移随时间的变化规律。隧道盾构施工引起的竖直测线L顶点处的水平位移为26.1 mm，随着深度的增加，测线L上的水平位移逐渐减小，并在隧道起拱线处达到最小值；起拱线以下的水平位移随深度先增大后逐渐不变，测线L的水平位移分布规律与衬砌椭圆化变形有一定的关系，衬砌拱顶向隧道中心移动，衬砌起拱线处同时远离隧道中心挤压土体，导致了测线L起拱线处的水平位移最小。另外由图可以看出，相对于地表沉降，软黏土流变对地层水平位移的影响较小，隧道建成100年后隧道起拱线处的水平位移只增加了1.6 mm。