高压环境下剪切稀化非牛顿撞击射流直接数值模拟

2019-07-18朱呈祥郑浩铭尤延铖

航空学报 2019年6期

朱呈祥，郑浩铭，尤延铖

厦门大学航空航天学院，厦门 361005

非牛顿撞击射流是凝胶推进剂在液体火箭发动机中破碎雾化的主要形式，它可以增强燃料的破碎雾化及其与氧化剂的有效掺混，进而增加燃烧效率。目前国内外学者针对非牛顿撞击射流雾化破碎的研究主要集中在相对较低的压力环境，而对撞击射流雾化过程中高压环境对非牛顿黏性的影响及其与流体破碎特征的关联知之甚少。但事实上，在真实的液体火箭发动机中，燃烧室压力通常在几兆帕，高的甚至可达20MPa，环境压力升高将必然改变撞击射流的雾化特征，形成与常压环境下截然不同的撞击雾化品质，进而诱发不同的燃烧现象，因此有必要针对高压环境下的非牛顿撞击射流开展专门研究。

Dunand等［1］发现在小气液动量比条件下射流雾化的难度随环境压力升高而增加。Shim等［2］对高压环境下的射流雾化进行了相关数值与实验研究，他们认为环境压力越大涡流越明显，且射流头部穿透力和射流宽度随环境压力增大而减小。Jung等［3］研究了高压环境下层／湍流液膜的破碎特征。他们认为，基于气体韦伯数可将液膜破碎分为3类机制：扩张破碎（Expansion Breakup），表面波破碎（Wavy Breakup）和雾化破碎（Catastrophic Breakup）。Kampen等［4］对牛顿流体及幂流流体破碎特征进行了对比，并给出各自破碎模式随韦伯数以及雷诺数的变化规律。Lee等［5］则通过对喷嘴几何尺寸及通用雷诺数对非牛顿射流破碎机理的影响研究，指出射流撞击破碎长度随广义雷诺数增加而下降，其雾化模态可分为预膜片型（Pre-sheet Formation）、射线型（Ray－Shaped）、液丝型（Ligament Structure）和完全破碎型（Fully Turbulent）4类。在国内，天津大学的杜青等［6］采用定容燃烧系统和三维多普勒技术（PDA）对高压下幂律流体射流破碎的粒度场分布进行了分析，但他们发现当喷射粒子经过测量中心时，其信息无法捕抓，因此需要通过反复调节接收器的位置来达到实验目标，其测量精度、测量效率和稳定性也仍有待提高。华中科技大学［7］、哈尔滨工业大学［8］、天津大学［9］、南京理工大学［10］、西安交通大学［11］、西北工业大学［12］、江苏大学［13］等单位也在该方向开展了系列研究。但截至目前，人们对高压环境下非牛顿射流撞击破碎机理的理解还非常模糊，更没有形成统一的方法和理论。

本文将采用直接数值模拟（Direct Numerical Simulation，DNS）工具，首次针对高压环境下非牛顿撞击射流开展液膜破碎特征及机理研究。以下将介绍所采用的数值方法与设置，撞击射流的三维结构、破碎特征和涡场特征等，并讨论液膜内的非牛顿黏性变化及其与常压撞击射流破碎的关联与区别。

1 数值方法

本文采用的是课题组自主开发的DNS程序FS3D（Free Surface 3D），该程序求解三维不可压Navier-Stokes方程组：

式中：u为速度矢量；ρ为密度；p为压力；t为时间；μ为黏性系数；k为外部作用力；T为气液两相分界面处的表面张力。FS3D程序采用流体体积（Volume of Fluid，VOF）［14］方法捕捉气液两相分界面，该方法定义变量f以表征单元格内的液体体积分数，其表达式为

为了精确描述气液两相分界面，FS3D程序运用分段线性界面计算（Piecewise Linear Interface Calculation，PLIC）［15］方法对界面进行重构。FS3D所采用的数值方法已在文献［16-17］中进行了气液两相液滴和瑞利破碎射流的实验验证，也说明了方法的可靠与准确性。

对于非牛顿黏性，本文用以模拟的幂律函数为

式中：μ0为零剪切时的动力黏度；γ为剪切率；K和n为取决于流体和环境的模型常数。该幂律本构模型可以很好地模拟随剪切率变化的流体黏度［18］，满足液体火箭凝胶推进剂流变学行为［19］，且已被 Motzigemba等［20］以及 Focke和 Bothe［21］验证过。此外，就非牛顿液态射流的黏性系数开展了基于 Schrder等［22］实验数据的验证［23］，并在常压环境下分析了非牛顿横向射流［24］、低韦伯数非牛顿撞击射流［25］和中等韦伯数非牛顿撞击射流的典型破碎雾化特征［26］。

与前期研究不同，本文将引入液体火箭发动机燃烧室内的高压因素，选取10MPa典型高压环境研究非牛顿撞击射流的雾化特征及机理。选用20%质量分数的Polyvinylpyrrolidone（PVP）水溶液为凝胶模拟液，该液体的Deborah数（De）和Elasto-capillary数（Ec）都在10－8量级，远低于黏弹性流体的极限值0.35和2.35，因此是一种典型的剪切稀化幂律流体。图1为本文采用的计算域示意图，L、W、H分别为长、宽、高，D为圆柱射流直径。双股非牛顿圆柱射流自垂直y轴的上下无滑移壁面中心以90°夹角相向喷入高压腔，前后左右4个面均为自由边界。为了充分利用该计算域，圆柱射流初始方向与x，y，z轴分别成45°夹角，双股射流于y＝H／2处撞击形成液膜并逐渐向下游发展破碎。计算域的长、宽、高分别为圆柱射流直径D的15、15和1.5倍，并采用512×512×128网格进行空间离散，最小网格尺度为4.69μm，与Kolmogorov尺度［27］（选取湍流长度尺度为射流直径的1／10，脉动速度取为射流速度的1／10，可以估算Kolmogorov尺度为4.91μm）在同一量级。

图1 非牛顿射流撞击计算域（2个射流喷嘴位于上下xOz面的中心）Fig.1 Computational domain for non-Newtonian impinging liquid jets（Two injectors locate at the center of upper and bottom wall in xOzplane）

表1给出了液体与气体的物性参数以及射流尺寸，U0为初始射流速度，σ为表面张力系数，下标l和g分别代表液体与气体。此外，表1还给出了基于式（7）和式（8）的液体与气体的雷诺数和韦伯数Re、Wel、Reg、Weg。这里特别关注气体的无量纲参数是因为本文考虑的计算域内充满高压空气，根据Lee等［5］的研究，气体的物性状态是决定射流破碎雾化特征的重要判据。

表1 计算参数设置Table 1 Summary of computational parameters

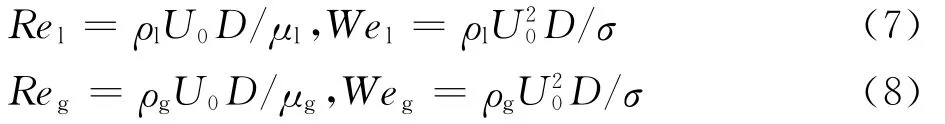
2 三维射流结构

双股射流以速度U0从直径为D的圆形喷嘴喷入图1所示高压计算域，在t＊＝tU0／D＝11.4时刻形成图2所示的撞击雾化结构，u为速度。可以发现，在双股射流撞击点附近及其下游区域仍然保持着低环境压力下的撞击液膜结构［26］，这与Bremond等［28］根据Wel划分的撞击射流结构是一致的。但与常压环境下撞击液膜存在明显的圆形 Rim［26］不同，高压下液膜边缘的 Kelvin-Helmholtz不稳定表面波随时间不断发展和破碎，在两侧及撞击点上游爆炸出大量液丝与液滴。

图2 t＊＝tU0／D＝11.4时刻撞击射流的三维结构（撞击液膜呈光盘状并伴有明细的液膜、液丝和液滴生成）Fig.2 Three-dimensional structure of impinging liquid jets at t＊＝tU0／D＝11.4 （A disk-shape liquid sheet is formed after iminement with obvious formation of sheets，liaments and drolets）

在图2所示时刻，撞击形成的雾化流场呈圆形辐射状分布，撞击点下游至头部的流体总长度Ld＝7.6D，而撞击点上游的流体总长度也达到量级相当的Lu＝6.3D，这与常压环境下的流体主要集中在撞击点下游也是截然不同的。此外，这里特别值得关注的是撞击液膜的头部特征，从图2可以发现其结构非常类似于Shinjo和Umemura［29］对单股圆柱射流在高压腔内喷注形成的蘑菇状头部的描述，表现为逆流向外罩的不断波动及破碎，只不过在本文研究的射流撞击过程中，该头部不是单股射流而是撞击形成的具有展向宽度的薄液膜。而且该头部结构在非牛顿黏性力作用主导下仅能维持在有限长宽范围内，超出后受气体力和表面张力作用主导破碎为液丝与小液滴结构，第3节将更详细地分析该非定常破碎过程。

图3 撞击射流表面积随时间的变化Fig.3 Temporal development of surface area of impinging liquid jets

液体的表面积大小直接决定气液两相的有效接触面积，因此对撞击雾化效果的评判具有重要意义。图3给出的是撞击射流过程中液体表面积随时间的变化规律，其中图3（a）为计算域内流体绝对表面积S的时域变化，图3（b）为无量纲表面积S＊的时域变化，本文定义S＊为绝对表面积S与单股圆柱射流表面积之比，S＊＝S／（πD2／4＋πDU0t）。可以发现，由于射流撞击雾化导致液膜、液丝及液滴的不断衍生，因此流体的绝对总表面积随时间逐渐增加，且增长斜率也随时间而增加。对于无量纲表面积而言，尽管其也随时间不断增加，但可以将时域变化大致分为5个阶段：t＊＜1.6，单独射流段；1.6＜t＊＜2，射流撞击段；1.6＜t＊＜5，射流撞击液膜发展段；5＜t＊＜9.5，液丝液滴爆炸段；t＊＞9.5，流体溢出段。在第1阶段，双股圆柱射流的头部受气体力作用向后翻折形成头盔状液膜，流体表面积相较初始圆柱射流显著增长；第2阶段在图3（b）中表现为短平直段，此时双股射流开始出现碰撞，导致部分液膜表面积消失，其速度与新液膜的生长速度相当；第3阶段为撞击液膜的快速铺展段，这也是射流撞击全过程中流体表面积增长最快的阶段；随后由于边缘液膜的破碎导致液丝液滴的爆炸性生成，流体表面积也进一步增加，此为第4阶段；在最后1个阶段，部分流体受空间限制已经溢出计算域，这部分溢出流体的表面积已无法进一步统计，因此计算域内S＊的增长速率变缓。

3 流动特征及机理分析

为了分析凝胶的撞击破碎雾化机理，本文给出了如图4所示的撞击射流对称面涡量场分布，这里定义无量纲涡量ω＊＝ωD／U0，其中ω为三维涡量的模。涡量能够反映流场中复杂的三维漩涡运动，可以发现，在气液两相分界面由于存在较大的气液速度梯度，因此气体中的涡量较高，而非牛顿液体受高黏性力影响其内部涡量相对较小。气体中涡量的分布又表现为有序贴附区和无序爆炸区两类，其中有序贴附区集中在双股圆柱射流和液膜初始段，无序爆炸区则主要集中在液丝液滴的生成区。图4（b）和图4（c）为放大的撞击液膜上、下游无序爆炸区，可以发现，图4（b）的局部流场中A和C处的非牛顿液体受气体力作用破碎产生的最小液滴尺寸已降至D／40量级，与Kolmogorov尺度相当，气体中的涡量分布与非牛液体的位置有极大关系，例如B处气体中出现的高涡量主要是因为撞击点上游液膜在该处出现表面波破碎导致了液膜表面的有序贴附涡量被表面波卷起。图4（c）的局部流场中可以观察到更为明显的撞击液膜表面波，其形成机理同样为高压气体引起的强气体力。在该时刻，图中所示4个表面波的波长基本相当，比例约为λ1∶λ2∶λ3∶λ4＝0.78∶1∶0.89∶0.78，各表面波虽然幅值不同，但颈部直径也均在D／15量级，这表明对液膜破碎起主导作用的气体力均在同一量级。

图5给出了俯视角下的双股射流撞击雾化三维特征及流场细节，非牛顿液体颜色代表无量纲速度u／U0，中切面内给出的仍为无量纲涡量ω＊。可以发现，尽管液体主要集中在撞击点下游，但上游液丝与液滴铺展极快，因此整个撞击射流破碎流场几乎呈正圆形分布，这与常压空气环境下的扇形破碎特征完全不同［26］。从图5（a）中还可以更明显地发现，气体涡量与液体体积分数的空间分布密切相关，本质上这是一种液体向气体的能量传输。此外，在液膜表面能观察到类似 Wavy破碎的表面波发展，图5（b）和图5（c）为局部流场细节，其中E处为典型的小液滴生成及液滴引起的局部气体涡量，F、G和H处为液膜边缘的表面波破碎区，可以观察到明显的液丝断裂与液滴生成。G处液丝形成近乎等距的多条状分布，液丝直径均相近约为D／10，液丝表面也开始呈现颈部特征，表明液丝断裂即将发生。这反映出2个流动机理，一是液膜向液丝的破碎主要受平均气体力和平均黏性力作用影响，因此会出现阵列式分布的宏观结构一致的液丝特征；而液丝向液滴的破碎则主要受局部流场参数影响，液丝的颈部及其断裂位置受局部不稳定扰动和非牛顿黏性影响较大，因此又具有不同的细节特征。

图4 撞击射流对称面涡量场分布Fig.4 Vorticity field distribution on symmetric surface of impinging liquid jets

图5 俯视角下双股射流撞击雾化三维特征及流场细节Fig.5 Three-dimensional characteristic and flow field details of two impinging jets atomization at depression angle

图6 为撞击射流的初始液膜形成的非定常过程。在t＊＝1.2时刻，双股圆形射流刚从喷嘴喷出，在气体力作用下头部射流上洗并形成了初始非对称蘑菇状。至t＊＝1.8时刻，射流撞击开始出现，撞击点液体融合形成初始液膜，蘑菇状头部也进一步发展。到t＊＝2.4时刻，撞击液膜快速展向扩张，并在撞击点上游出现破碎及液滴生成，上下侧蘑菇状头部也开始融合并形成了黑线所示类似Ω的截面局部凸起。t＊＝3.0时刻，蘑菇状头部进一步发展拉伸，Ω特征也更趋明显，液膜向撞击点下游继续铺展并在边缘处出现破碎形成液丝。此时，撞击形成的液膜在流向长度上已经赶超蘑菇状头部，形成特殊的尖前缘蘑菇状的头部特征并一直延续到t＊＝4.2时刻。上文提及的Ω局部凸起也在气体力的作用下于t＊＝3.6开始出现破碎并于t＊＝4.2时刻完全破碎，此时蘑菇状头部的台阶特征开始出现，在随后不断发展过程中，液丝与液滴的生成将成为该处的主要细节流动现象，如图7所示。在t＊＝8.4时刻，该蘑菇状头部液膜具有表面波特征，其波长约为原射流直径D的0.7倍。随着时间发展，该表面波在头部液膜边缘处先出现破碎特征，并逐渐向中心撕裂，至t＊＝9.6时刻表面波的固定波长特征已经基本消失，t＊＝11.4时更是仅剩紊乱的液丝与液滴结构。与分析牛顿流体破碎特征不同，研究非牛顿流体破碎需要兼顾流体黏性的非定常变化，尤其是局部剪切不同引起的流体黏性系数差别。

图6 t＊＝1.2～4.2时撞击射流表面凹穴破碎的时序发展Fig.6 Temporal development of surface cavity breakup of impinging liquid jets fromt＊＝1.2to 4.2

图7 t＊＝8.4～11.4时撞击射流表面波破碎的时序发展Fig.7 Temporal development of surface wavy breakup of impinging liquid jets fromt＊＝8.4to 11.4

4 非牛顿特性

本文研究的剪切稀化非牛顿流体其黏性系数随剪切率的升高而降低，在10MPa高压环境下，气液两相间的强剪切力将带来撞击射流明显的非牛顿特性，图8给出了撞击射流对称面内的无量纲非牛顿黏性系数（μ／μ0）分布及其沿对角中心线的分布。

从图8可以发现，流体的黏性在对称面内呈现两端低中间高的分布规律，在撞击点上游，由撞击形成的高剪切使得非牛顿流体无量纲黏性系数下降至0.7，在上游液膜、液丝及液滴中，黏性系数更是低至仅0.3左右。黏性系数的降低不断削弱流体的抗剪切能力，也使其更易破碎，因此撞击点上游液滴的形成也更为彻底。在撞击点下游，液体趋近同向流动，剪切的减弱导致黏性系数逐步回升至约0.9，但在上文提及的中心液膜表面波处，液体的黏性系数同样随表面波上下波动，表现为高低交替分布规律，其中颈部的黏性系数较低，约为0.8，而液节中的黏性系数较高，约为0.9。此外，在射流头部，由于高压气体的强剪切作用，液体的黏性系数突降至约0.7，这也意味着该局部的液体破碎将遵循用当地物性参数表征的破碎模态，亦即相较同等条件的牛顿流体将更易破碎［25］。

图8 撞击射流在x（z）y对角面内及其中心线上的非牛顿黏性系数分布Fig.8 Distribution of viscosity in the x（z）y diagonal plane and along centerline of impinging liquid jets

5 讨论

非牛顿撞击射流的破碎雾化特征直接影响着燃料最终的掺混及燃烧。通过改变喷注参数和环境参数，等直径非牛顿直角撞击射流的非定常流态及剪切稀化黏性均发生剧烈变化。在常压条件下，低韦伯数射流撞击形成的单一对角射流包含头部液滴破碎和液柱破碎2种形式，其中头部液滴破碎属于瑞利破碎，液柱破碎属于弯曲波破碎［25］；而中等韦伯数射流撞击形成的液膜破碎属于 Open Rim类别［26］，其破碎过程具有典型三维特性并伴随液丝与边缘的融合、液丝向液滴的转变等时域流动特征。在本文研究的高压环境下，尽管在撞击点附近仍保持着常压条件下的液膜结构，但液膜边缘爆炸出大量液丝与液滴而非常压条件下的圆形Rim结构，同时撞击射流头部形成具有展向宽度的蘑菇状液膜和Ω形局部凸起，这将有助于后续燃烧的发生。在非牛顿黏性方面，由于所研究的撞击射流的流态差别较大，而流态又直接决定了流体各处异性的剪切和局部黏性，因此作者在分析流体内部非定常非均匀黏性时仅提取了具有代表性的对称面和中心线的参数分布，还不足以表征全流场的非牛顿黏性变化，后续有必要对相关分析方法作进一步提炼。