阶梯型舱壁次要支撑构件的弯矩因数取值改进

黄晓丰

(上海欧得利船舶工程有限公司, 上海200023)

0 引 言

常规油船的泵舱前端壁通常为垂直平板舱壁，如图1所示。随着压载水处理装置的使用，泵舱布置设计较常规发生变化，需要更大的空间。为满足设备的布置要求，需对泵舱进行优化设计[1]，通常将泵舱向污水舱延伸，使泵舱前端壁呈现阶梯形状，如图2所示。现行IACS《油船和散货船共同结构规范》[2](下文称“规范”)对于此类阶梯型舱壁上的次要支撑构件的弯矩因数并未作出明确规定，给设计工作及工程实践带来诸多不便。本文以采用此种结构形式的一型油船泵舱为例，通过有限元计算方法对阶梯型舱壁次要支撑构件的弯矩因数取值进行研究，使该处的结构强度满足规范要求，且具有一定的强度储备[3]，同时提出此类阶梯型舱壁的设计方案及注意事项，为实际工程应用提供参考[4]。

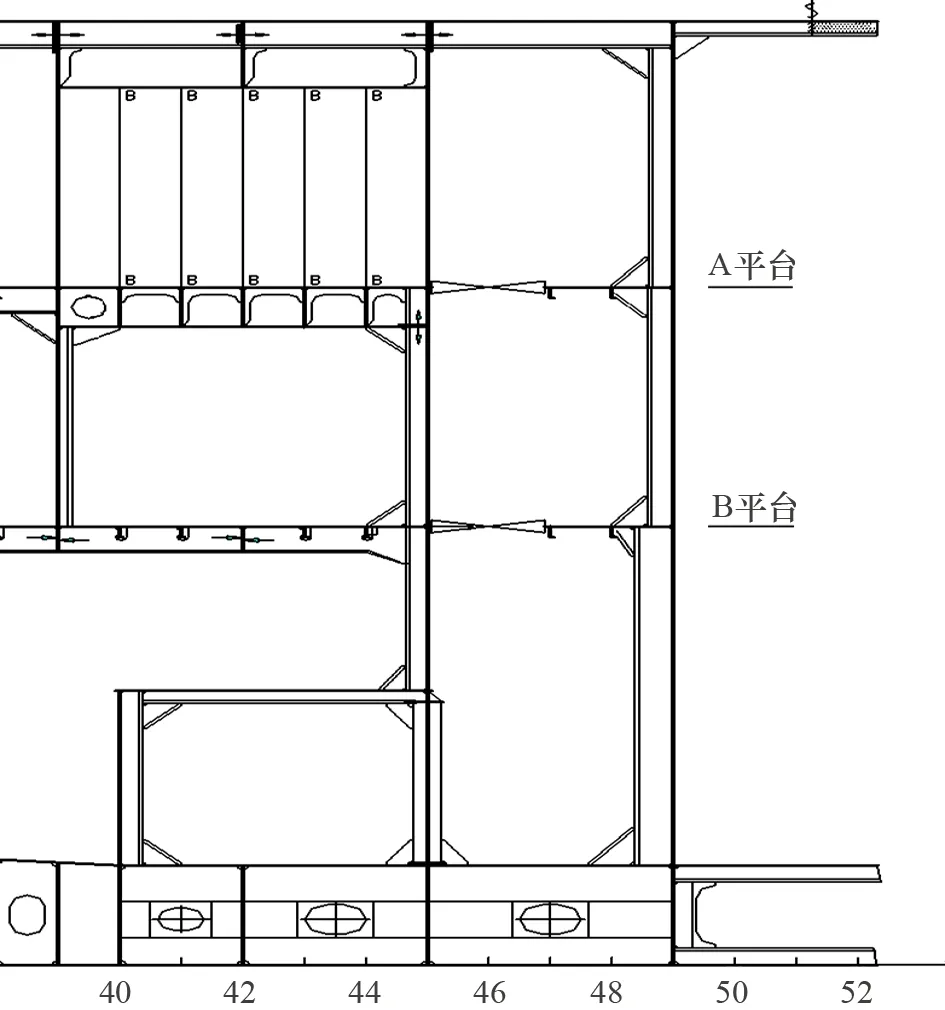
图1 泵舱前端平直舱壁

图2 泵舱前端阶梯型舱壁

1 次要支撑构件弯矩因数规范要求

规范第6.6节对局部和次要支撑构件的尺寸作出要求，第6.3.2.1节给出次要支撑构件所要求的弯矩因数，如表1所示。

表1 弯矩因数取值表

对于承受侧向压力、点载荷或其他载荷组合的加强筋，要求净剖面模数应为所有设计载荷组合计算所得结果的最大值，最小净剖面模数Z应不小于

(1)

式中：P为考虑设计载荷组合下，计算点计算所得设计压力，kN/m2；s为次要支撑构件间距，mm；lbdg为有效弯曲跨距；fbdg为弯矩因数；Cs为考虑设计载荷组合下的许用弯曲应力因数；χ为对不同工况的修正因数，在完整工况下，χ=0.90(对于连接在散货船货舱内的内底板或底边舱斜板上的骨材)，χ=1.00(对于其他情况)；ReH为所考虑扶强材材料的最小屈服应力，N/mm2。

垂直型舱壁的次要构件主要承受侧向线性变化压力载荷。根据规范要求：两端刚性固定的扶强材在三角形分布载荷作用下，构件最下端适用的弯矩因数fbdg=10；一端刚性固定一端简支固定的扶强材在三角形分布载荷作用下，构件最下端适用的弯矩因数fbdg=7.5。规范还指出，对于端部约束减弱、载荷变化或者作为板架一部分的骨材，须进行直接计算校核。

2 阶梯型舱壁次要支撑构件弯矩因数取值

为保证阶梯形舱壁结构相关设计节点的强度安全，有必要对阶梯型舱壁次要支撑构件的弯矩因数进行分析。图2中泵舱前端壁存在两处舱壁折角点，其余两段平直舱壁的另一端分别连接主甲板和内底板。主甲板和内底板属于强构件，舱壁与其连接的位置可作为刚性固定端。为研究阶梯型舱壁次要构件弯矩因数的取值规律以及解决此类设计问题的其他方法，本文采用有限元法对阶梯型舱壁的次要支撑构件尺寸进行直接计算校核，并对阶梯型舱壁次要支撑构件的弯矩因数取值进行对比验证[5]。

取阶梯型舱壁的次要支撑构件为分析对象，建立三维有限元模型[6]，如图3所示。为计算阶梯型舱壁上的次要构件尺寸，以舱壁水平桁支撑处和两折角点处为扶强材端点量取跨距、共计5段，扶强材编号如图3所示。将阶梯型舱壁的上下两端取为刚性固定端,将水平桁处取为简支固定端，折角处的边界条件视设计情况而定。

图3 阶梯型舱壁的次要支撑构件三维有限元模型

2.1 阶梯型舱壁次要支撑构件计算结果分析

设计之初，假设在阶梯型舱壁的折角处设置了平台或强有力的水平桁支撑舱壁扶强材，则可认为折角处为刚性固定边界。模型边界条件和载荷分布如图4和图5所示。根据规范公式(1)的计算方法，采用弯矩因数fbdg=10计算阶梯形舱壁上所有垂直扶强材尺寸大小。然后建立有限元模型，对根据前述方法取得的构件尺寸进行计算校核，计算结果如表2所示。从表2的计算结果可见，采用弯矩因数fbdg=10取得的构件尺寸在折角处刚性固定的条件下满足规范要求。

图4 折角处为刚性固定约束的边界条件

图5 线性载荷分布

表2 舱壁正中间一列扶强材应力计算结果

由于管系布置或空间原因无法在折角处设置强支撑构件的情况下，折角处结构的边界约束并非刚性固定，模型中折角处的边界约束须释放掉，以反映真实的折角处相邻扶强材之间的相互支撑关系，有限元模型边界条件如图6所示，可见载荷分布与图5一致。

图6 折角处无约束的边界条件

根据表2的计算结果，采用弯矩因数fbdg=10取得的构件尺寸在折角处无端部约束的情况下，1#、3#、4#扶强材的合成应力值超过了许用应力值，不能满足规范要求。从图7所示的扶强材变形图可以看出，在单侧载荷的影响下，1#、2#、3#扶强材整体呈塌陷状， 2#扶强材的整体位移偏大。

图7 扶强材变形图

2.2 阶梯型舱壁次要支撑构件弯矩因数取值改进

综上可见，弯矩因数fbdg=10不适合作为折角处相连构件的剖面模数计算输入值，在不能设置水平桁或者平台等强构件对舱壁折角处进行水平支撑的情况下，只能通过增大扶强材的构件尺寸保证结构安全。经过迭代试算，当弯矩因数取fbdg=3时，对应的扶强材尺寸经有限元验证可满足规范要求，计算结果如表3所示。从表3可见，在仅增加1#、2#、3#扶强材构件尺寸的情况下，其本身刚度变大，扶强材之间相互支撑的作用增强， 4#扶强材的应力水平也显著下降。

表3 舱壁正中间一列扶强材增加尺寸后的应力计算结果

3 结 论

现行IACS《油船和散货船共同结构规范》中次要支撑构件的有效剖面模数计算公式适用于垂直舱壁上支撑构件的设计，对阶梯型舱壁次要支撑构件的弯矩因数未作任何规定，规范虽提及对于端部约束减弱等情况的骨材须进行直接计算校核，但是哪些属于端部约束减弱的情况，主要依靠审图师和设计人员的主观判断。本文针对阶梯型舱壁可能存在的设计隐患，对其次要支撑构件进行有限元计算，提出一种阶梯型舱壁次要支撑构件弯矩因数取值的改进方法。

对于阶梯型舱壁的结构设计，折角处的节点设计尤为重要。当折角处设置了平台或强有力的水平桁时，对相连扶强材可形成有效支撑，计算扶强材尺寸时可视为刚性固定边界，弯矩因数取fbdg=10。如因布置或空间原因无法在折角处设置强支撑构件时，扶强材的边界条件近似为弹性简支固定，计算扶强材尺寸时弯矩因数可取fbdg=3，或者采用直接计算方式评估扶强材强度，通过适当加大折角处相连扶强材的尺寸，保证结构安全。该取值改进方法为解决相关工程设计问题提供了一定的参考。