基于微分平坦理论的直流电机控制系统设计

于仲安， 张峻铭， 王先敏

（江西理工大学电气工程与自动化学院，江西 赣州 341000）

0 引 言

直流电机是传统电机之一，出现19世纪后期.与其他电机如感应电机[1-2]、无刷直流电机[3]相比，直流电机具有一些优势，如控制简单、电磁转矩大、具有调节速度的能力、应用范围广[4].因此，直流电机通常用于工业领域，如轧钢、运输、采矿、国防、建筑[5-7].直流电机多采用传统的PID控制，PID控制是最早发展起来的控制策略之一，由于其具有算法简单、鲁棒性好和可靠性高等优点，被广泛应用于工业过程控制中.直流电机控制系统中存在很多非线性或时变的不确定因素，使PID控制的参数无法准确整定，控制效果也因此而受影响，并且容易出现超调、震荡等问题.控制非线性对象有几种解决方案，如输入、输出线性化控制技术[8]，滑动控制技术[9]，反步控制技术[10]等.这些控制策略的控制效果不错，但控制算法复杂.基于微分平坦控制的直流电机控制系统采用由前馈控制量和误差反馈补偿组成基于平坦控制策略能够很好地解决这个问题.文中设计的直流电机控制系统提高直流电机的响应速度和动态性能，也解决了传统PID控制产生的超调问题.

微分平坦理论是由Fliess等在20世纪90年代针对非线性系统提出的一个概念.微分平坦理论指出了非线性系统动力学特性的一种结构形式的存在性，也就是平坦输出的存在性，意味着通过选择合适的平坦输出可以使非线性系统线性化[11].通过系统的微分平坦特性实现实时轨迹的跟踪.如机器人的轨迹规划[12]、自主泊车轨迹规划等.微分平坦控制系统最重要的是确定平坦输出变量z集合的存在性,通过z变量和z变量的微分,可以确定所有状态变量和输入变量.由于微分平坦系统的状态量和输入量可以由平坦输出直接表示，那么根据期望的平坦输出轨迹，就能直接得到期望的状态变量和输入变量不带延时的轨迹[13].

1 直流电机的微分平坦控制理论的验证

直流电动机的等效电路结构如图1所示，其中包括转子中的电枢线圈和定子中的励磁线圈.

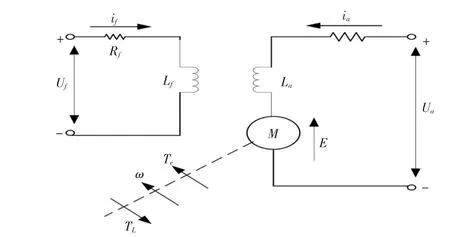
图1 直流电动机的等效电路结构

图1 中Ua为电机电枢端电压，E为电机反电动势，Ra为电枢电路电阻，La为电枢电路电感，ia为电机电枢电流，Rf为励磁电路电阻，if为电机励磁电流，Lf为励磁电路电感，Te为电机转矩，TL为电机负载转矩，ω为电机的角速度，Uf为电机的励磁电压.

为了证明直流电机是微分平坦控制系统，首先必须确定直流电机的数学模型，以证明直流电动机满足微分平坦控制系统的条件.根据基尔霍夫电压定律(KVL)，可得直流电机的电枢的电压公式：

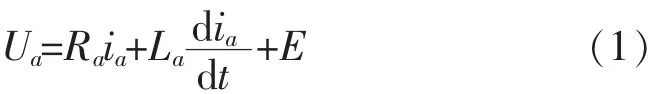
式 （1）中：Ua为电机电枢端电压；E为电机反电动势；Ra为电枢电路电阻；La为电枢电路电感；ia为电机电枢电流.

而电机反电动势可以表示为：

式（2）中：KE为反电动势的电压系数；ω为电机的角速度；Laf电枢电感与励磁电路的互感；if为电机励磁电流.

直流电机的运动方程表示为：

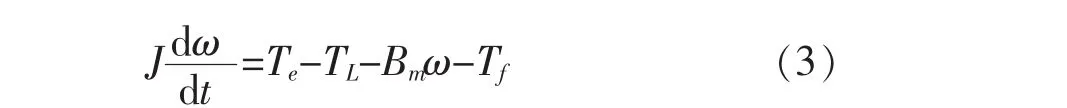
式（3）中：J为电动机轴上的转动惯量，Bm为粘性摩擦系数，Tf为库仑摩擦转矩，Te为电机转矩，TL为电机负载转矩.

电机转矩方程表示如下：

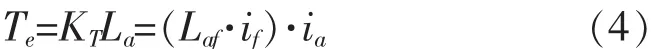
式（4）中：KT是转矩系数.

微分平坦控制理论用来控制非线性对象的控制方法，先假设一种非线性的状态控制方程如下[11]：

式（5）中：u=（u1，u2，…，um）T是输入变量，x=（x1，x2，…，x3）是状态变量.

如果存在一组变量 z=（z1，z2，…，zm）满足以下三个条件，变量z被称为平坦输出变量，则状态控制方程为公式（5）的控制系统被称为微分平坦控制系统.

根据直流电机的方程式，令 x=（ia，ω），u=Ua，即电机电枢电流和电机的角速度为状态度变量，电机电枢端电压为输入变量.由式（1）和式（3）联立可得状态方程：

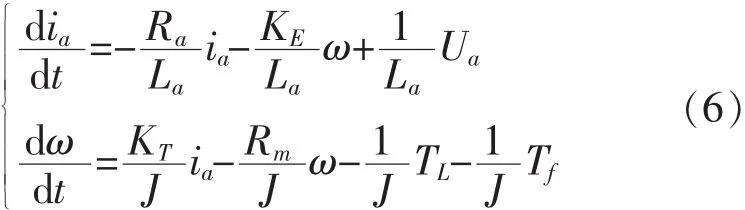
条件a：存在一个函数h，满足以下公式：

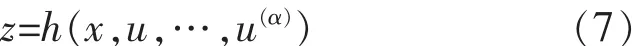
选择平坦输出的变量为z=ω，可以从公式（6）很容易得出存在函数h满足公式（7）.

条件b：所有输入变量和状态变量都可以由变量z确定，存在着有函数A和函数B满足以下公式：

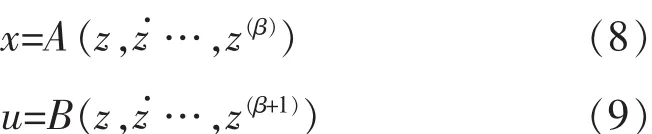
通过变化公式（6）的第一个公式可以得到：

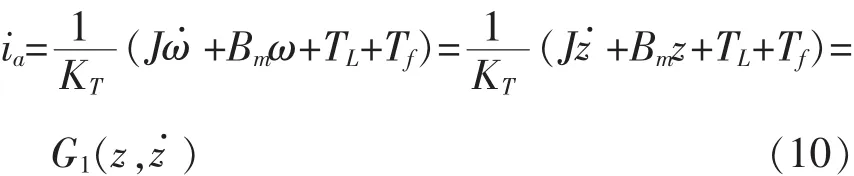
所以存在函数A使得x=（ia，ω）=A（z，）.

通过公式（1）、公式（2）、公式（3）和公式（4）的代入变化可以得到：

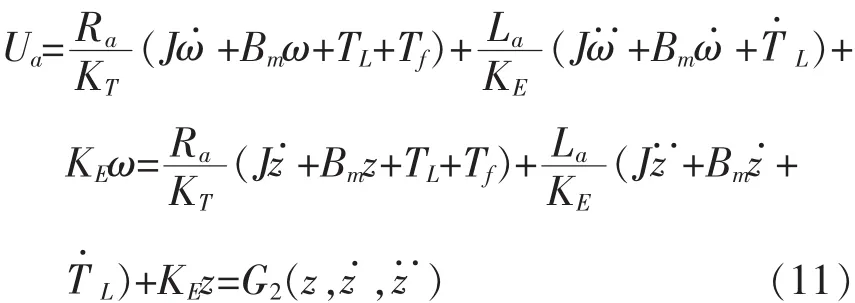
所以存在函数B使得u＝Ua＝B（z，，）.因此可以得出结论，满足直流电机可以满足第二个条件.

条件c：z的所有变量都是独立的微分，不存在函数G满足以下公式：

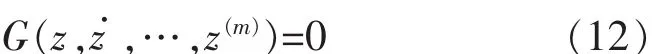
z=ω的所有变量都是独立的微分，这是显而易见的，因为只用一个变量z作为平坦输出.根据以上的证明得出结论，直流电机是微分平坦控制系统，平坦输出是z=ω.

所以该非线性系统称为微分平坦系统.对于微分平坦系统，状态变量x和控制变量u与输出量z存在一一对应关系，且z和u的维数相同.z可以任意选取，可按照实际需要选取z来设计基于平坦控制，但有一些系统本身的输出就能作为平坦输出[14].

2 直流电机微分平坦控制系统的设计

根据上述可知，直流电机微分平坦控制系统由前馈控制量的产生和误差反馈补偿两部分组成，根据式（6）生成前馈控制量，为了消除扰动所产生的误差，在误差反馈加入PI控制，最终使输出的转速完全跟随期望的转速的轨迹.

由式（6）可得期望前馈控制量：

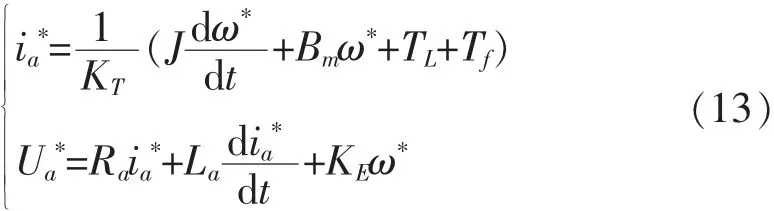
其中，上标*表示期望值.

令状态误差变量Δω=ω-ω*，可得误差：

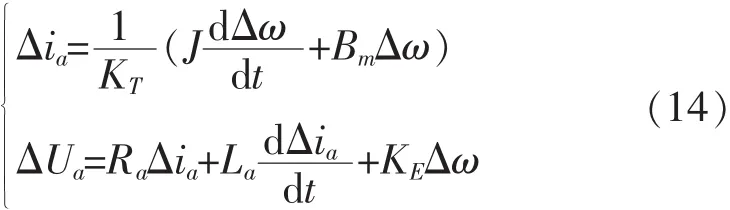
加入PI控制并由上式可得误差反馈补偿：

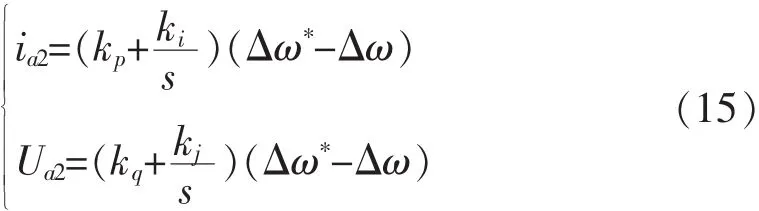
其中，kp，ki，kq，kj为 PI控制的参数， 为了使反馈误差为0，令Δω*=0，则基于微分平坦的控制量：

设计直流电机微分平坦控制系统框图如图2所示.

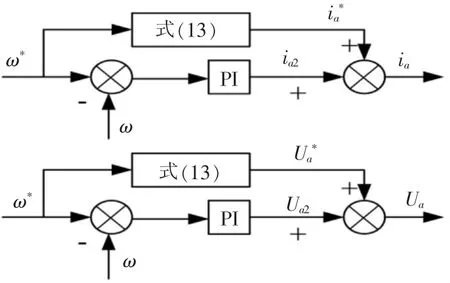
图2 直流电机微分平坦控制系统框

3 仿真分析

使用Matlab/Simulink搭建直流电机微分平坦控制控制系统和传统PID控制系统，仿真所用直流电机的参数如表1所示.图3为直流电机的微分平坦控制控制框图，其中速度控制器和电流控制器为图2设计的微分平坦控制系统.而PID控制的参数通过参考文献 [15]的公式计算Kp=12.8，KI=0.084，KD=0.0028.

速度控制器和电流控制器中的PI控制的参数通过工程整定得到.

以初始设定角速度ω=120 rad/s进行直流电机微分平坦控制系统仿真，然后在时间t=1.5 s时速度的设定为ω=150 rad/s，在t=3 s时速度的设定为ω=180 rad/s.初始负载扭矩TL=50 N·m，然后在时间 t=4.5s和t=5.5s， 将TL增加到200N·m和400N·m进行仿真，仿真结果如图4所示.图4（a）是直流电机微分平坦控制角速度的波形，图4（b）是直流电机PID控制角速度波形，可以看出微分平坦的超调量更小，有较强的鲁棒性.图4（c）是直流电机角速度波形比较，虚线表示设定的角速度，实线表示实际的角速度.可以看出实际角速度波形和规划的角速度很好的重合，那就达到对直流电机角速度规划轨迹的精确跟踪.如图4（d）是电机负载转矩与角速度的波形，可以当负载转矩在4.5 s和5.5 s变化时，电机的角速度经过很短的调整又回到原来的值，说明了整个直流电机系统动态特性较好.

表1 直流电机的参数

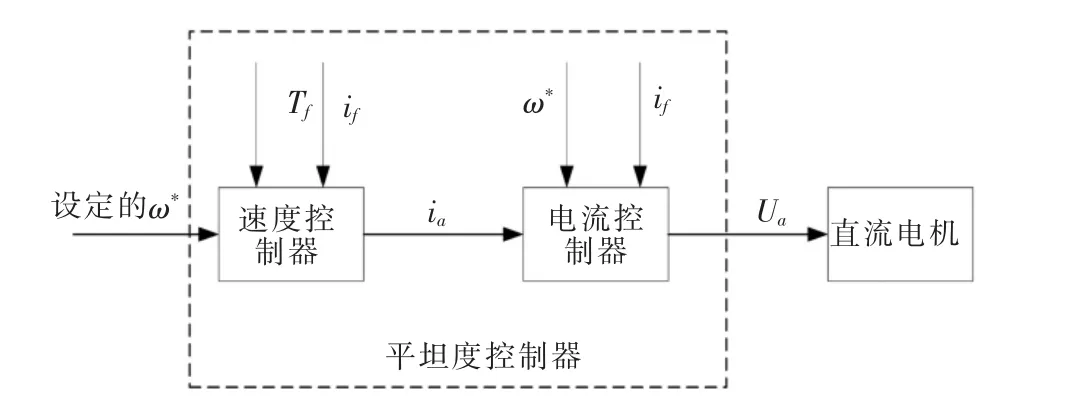
图3 直流电机控制系统

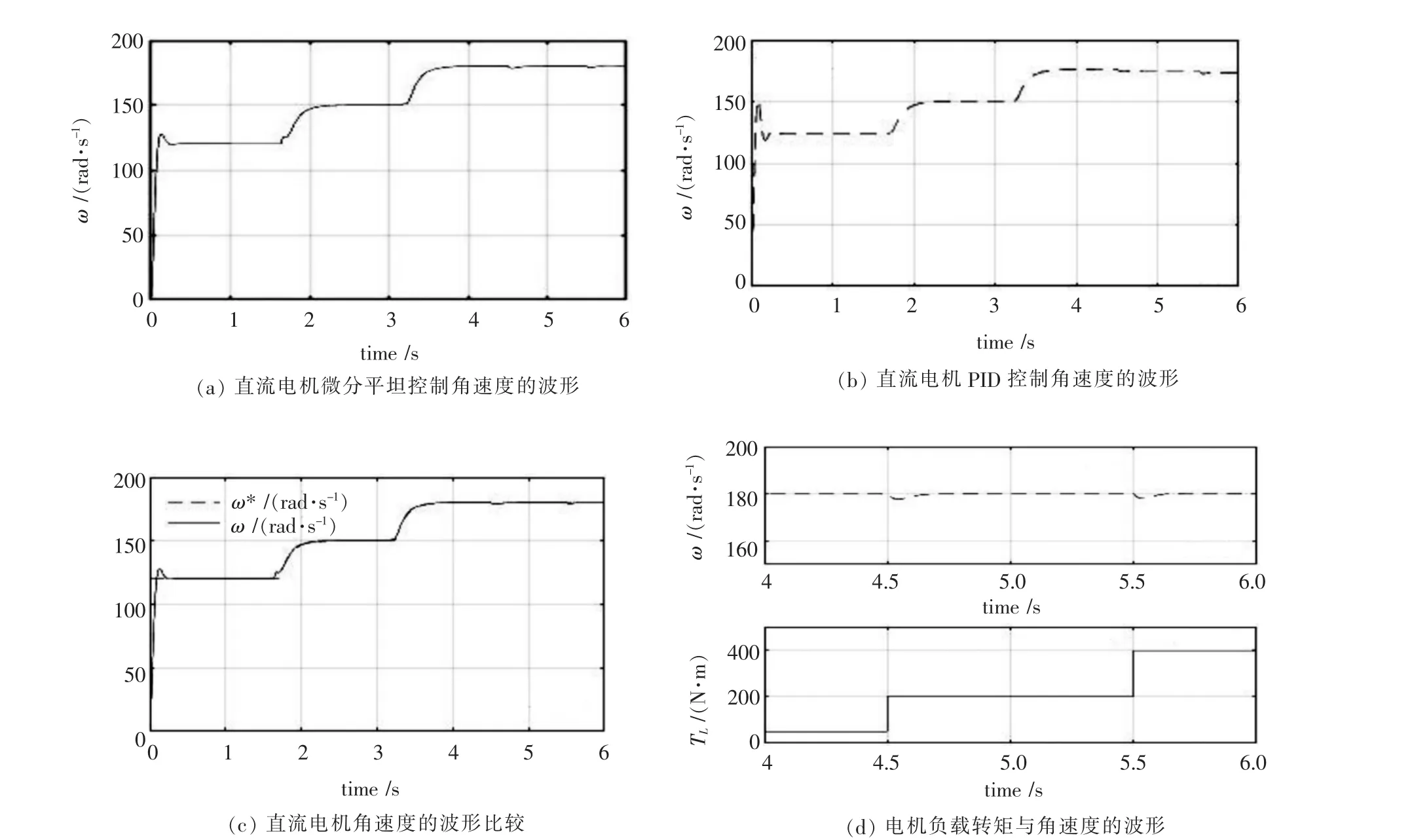
图4 直流电机微分平坦控制系统仿真波形

4 结 论

文中简单介绍了微分平坦控制理论的原理及平坦控制的框架，直流电机的数学模型及对其微分平坦系统的验证.设计了直流电机微分平坦控制系统，包括控制量的生成和误差反馈的补偿，进行仿真比较分析.结果表明，本文提出直流电机微分平坦控制系统可以很好对角速度的轨迹进行预测.当负载转矩变化时，控制系统能快速调整，整个直流电机控制系统有较好动态性能.