一种附带缓和曲线的多边形构建方法
2019-07-10黄烈星康俊锋温小军张春艳
黄烈星, 康俊锋, 温小军, 张春艳
(江西理工大学建筑与测绘工程学院,江西 赣州341000)
0 引 言
多边形的周长计算、面积计算和布尔运算在实际测量工作中都有着重要的应用[1-3].测量工作中有时需要处理含有缓和曲线多边形,这类多边形比普通多边形更加难以处理而且情况复杂.目前,国内外许多学者分别对缓和曲线和多边形处理问题进行了深入研究,并提出了各自的算法.针对缓和曲线的计算与处理,冯晓等[4]针对不同类型缓和曲线正算与反算的通用算法进行了研究,提出了缓和曲线坐标计算方法;殷海峰等[5]则提出了可以从任意一点开始起算,并且计算项数可以进行灵活扩充的缓和曲线的正算与反算的通用算法.针对多边形的面积处理,李亚玲[6]在多边形面积的计算与面积法的应用中,分析总结了多种多边形面积计算方法;李凯等[7]提出了平面六边形格网面积计算公式并进行验证.针对多边形的布尔运算,Vatti B R[8]和Greiner Hoemann[9]在针对点数较大多边形布尔运算问题,分别提出了Vatti算法和Greiner Hoemann算 法;Francisco Martínez 等[10]针 对含孔洞的凹多边形的布尔运算问题,提出了一种简单易懂,便于实现的算法;彭杰等[11]针对多边形布尔运算问题,提出了一种基于交点排序的算法;Francisco Martínez等[12]针对凹多边形,带孔的多边形,多个轮廓和自相交边的多边形提出了高效的布尔运算算法.赵军等[13]提出了基于最小回路确定孔洞多边形P和多边形Q的交、并、差计算方法解决了孔洞多边形的布尔运算问题;齐东洲等[14]针对多边形的布尔计算提出了一种基于交点的多边形并交差算法,该算法采用循环单链表数据结构,能够很好地处理一些包括重叠边、交点为边的顶点等边界情形.刘思远[15]则通过交点处四个矢量边的运算决定交并差结果环的走向,避免了二维布尔运算中的重点、重边等奇异问题;黄志等[16]针对多边形集合的求交问题,提出了基于多级格网的多边形集合求并算法;S a^m Landier[17]则提出浮点算术算法用于解决上任意多边形和多面体网格的布尔运算问题.这些研究成果为缓和曲线及多边形处理问题提供了理论基础,但是针对复杂嵌套且附带缓和曲线的多边形处理问题鲜有研究.本文主要从缓和曲线,多边形的几何特点对缓和曲线和多边形进行建模,构建出附带缓和曲线的多边形模型,实现了附带缓和曲线多边形的周长计算、面积计算和布尔运算.
1 附带缓和曲线多边形模型
本节将介绍附带缓和曲线多边形模型中涉及的一些概念和基本原理.
1.1 附带缓和曲线多边形定义
多边形是由三条或三条以上的线段首尾顺次连接所组成的平面图形.在普通多边形中线段主要为直线段与圆弧段,而测量多边形中可能会含有缓和曲线段.为了便于描述,称含有缓和曲线段的多边形为附带缓和曲线多边形.附带缓和曲线多边形可以含有一条或多条完整缓和曲线(部分缓和曲线段).测量工作中,可能会遇到多个多边形嵌套构成的图形.为了结合测量实际工作,文中所指附带缓和曲线多边形模型为一个或多个相互嵌套但不相交的含缓和曲线段多边形的集合.如图1所示为一个复杂嵌套附带缓和曲线多边形,图1中的23段与45段为缓和曲线段,该多边形由4个多边形嵌套组成.
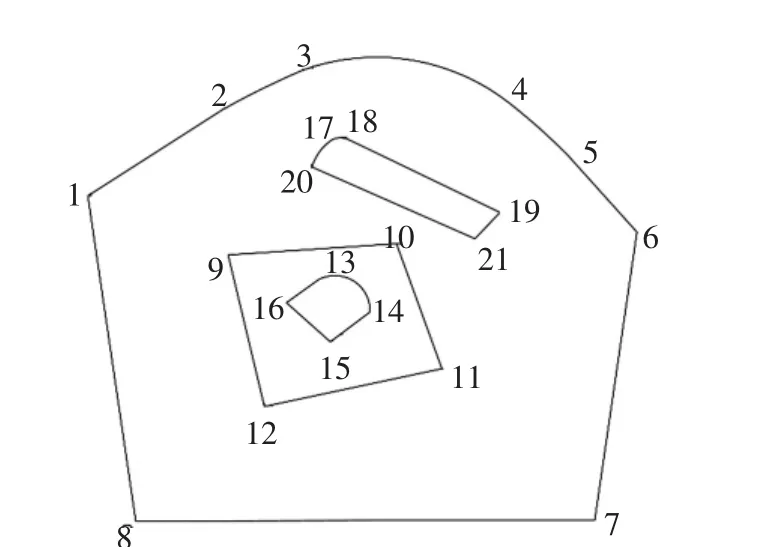
图1 附带缓和曲线多边形
1.2 附带缓和曲线多边形模型构建
在对多边形模型构建前,需要先构建线段模型.附带缓和曲线多边形模型中包含的线段有:直线段、圆弧线段、缓和曲线段.
1.2.1 线段模型构建
在线段模型中,直线段构建较简单.构建的内容主要有直线的起点,直线的终点以及直线交点计算[18].圆曲线段用圆弧线段表示,圆弧线段的主要内容有圆弧的圆心、半径、圆弧起始角度、圆弧终止角度.在多边形中,圆弧主要涉及圆弧与圆弧交点计算,圆弧与直线交点计算[18].
缓和曲线段内容主要包括缓和曲线数据结构设计[19],缓和曲线段算法设计.缓和曲线段的处理主要包括坐标转换和交点计算.坐标转换指的是将测量坐标系坐标转换为缓和曲线坐标系坐标;交点计算包括缓和曲线段与直线段交点计算,缓和曲线段与圆弧段交点计算,缓和曲线段与缓和曲线段交点计算.
1)缓和曲线段数据结构
缓和曲线:缓和曲线的起点,缓和曲线的终点,缓和曲线的长度,缓和曲线的方向角,半径,是否右转以及缓和曲线方向是否与线前进方向一致等属性,具体如表1所示.
2)缓和曲线段的交点计算
缓和曲线段计算中最重要的是坐标计算,根据缓和曲线的长度,半径等关系得出缓和曲线段任意点的坐标.关于缓和曲线坐标计算,李伟等[20]和殷海峰等[5]提出了切实可用的算法.其次是缓和曲线段与直线段,圆弧段,缓和曲线段的交点计算.对于交点计算,采取思路为:将缓和曲线按一定间距分段成a段直线段 (为了保证计算精度定义a>20,a可以根据实际情况进行修改),将每个直线段分别与直线段或者圆弧段进行交点计算,交点计算的结果为缓和曲线与直线的交点结果.缓和曲线段与圆弧段以及缓和曲线段与缓和曲线段算法思路类似.

表1 缓和曲线的属性
1.2.2 多边形模型构建
1)判断点与多边形关系
在进行附带缓和曲线多边形构建与布尔运算时需要多次判断某个点是否在多边形内部.判断一个点是否在多边形内部有多种方法[21],文中算法采用引射线法判断点是否在多边形内部,基本原理如下:以测试点为基点,分别以向左和向右做射线.射线分别与多边形所有线段求交点,去除奇异情况后,统计交点个数.如果测试点两边的左右两边交点个数都是奇数则该测试点在多边形内,否则在多边形外,示意图如图2所示.

图2 判断点在多边形内部
2)判断多边形与多边形关系
在构建多边形模型时,需要判断多边形之间关系.对于多边形A和多边形B,将A中所有圆弧线段顶点进行是否在B中判断,如果A中有部分点在B的内部也有部分点在B的外部则认为多边形A和多边形B相交.如果A所有的点均在B的内部,则认为B包含A.如果A的点均在B的外部则A与B相离.
3)多边形模型
直线段、圆弧线段、缓和曲线段有序组合成一个闭合环;一个或多个不相交的环嵌套组成多边形,这里将组成多边形的环主要分为:外部环(没有被任何多边形包含)、内部环 (被奇数个多边形包含)和岛环 (被偶数个多边形包含).构建多边形时,首先判断多边形之间是否相交,若相交,则不能构成多边形.算法中,采用层状结构存储多边形,较常规树状模型存储多边形而言不仅能够降低运算难度,而且能够提高运算效率.
如图3所示的多边形示意图中,1为外部环,2、3、4 为内部环,5、7 为岛环,6 为内部环.按层存储多边形时,1 为第一层,2、3、4 为第二层,5、7 为第三层,6为第四层;按环类型存储时分为外部环集、内部环集和岛环集.
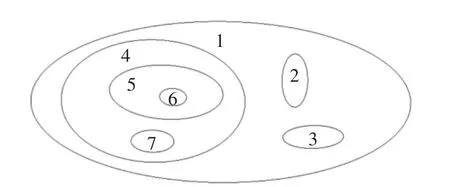
图3 多边形示意
2 附带缓和曲线多边形处理算法
多边形的布尔运算,即多边形的交、并、差,是计算机几何和计算机图形学领域的基本问题.布尔运算在图形处理过程常用于基本图形组合以产生新的形体.多边形的面积与周长计算也是多边形的处理必不可少的算法.本节重点介绍附带缓和曲线多边形布尔运算、面积计算与周长计算的算法思路.
2.1 数据预处理
在对多边形处理前先对多边形进行预处理.如图4所示,为一种典型的附带缓和曲线多边形,M1与M2均为嵌套多边形,其中M2为附带缓和曲线段多边形,9号点为直缓点,10号点为缓圆点,23号点为圆缓点,11号点为缓直点.M1的内部与M2的内部有相交部分.将M1中的外部环和岛环按顺时针存储,内部环按逆时针存储;将M2中所有环层中的外部环和岛环按逆时针存储,内部环按顺时针存储.其中M1、M2均由一个外部环和一个内部环构成,M1的外部环结构为:19-20-21-22-2-3-23-24-4-1-19,内部环结构为:9-25-5-26-12-7-6-9;M2的外部环结构为:19-15-24-14-23-13-12-11-10-9-22-8-19,内部环结构为:20-16-21-25-17-26-18-20.

图4 多边形预处理
2.2 多边形布尔计算
2.2.1 多边形中的线处理
对两个多边形进行布尔运算时,需要判断多边形的线是否在另一多边形内部,并对线做标记.类比于多边形环的分类,将线分为外部环线L1、内部环线L2和岛环线L3.线标记准则如下:线默认标记为0;L1和L3在外部环或岛环的内部标记1;L1和L3在内部环的内部标记2;L2在外部环或岛环的内部标记3;L2在内部环的内部标记4.算法步骤:对于线L,按照环层顺序(0-n)处理,对环层中每个环都进行线L是否在内部的判断,若线在内部,则根据标记准则对线进行标记,否则不做处理;对多边形预处理后,分别对M1、M2的线进行标记处理,结果如图5所示.
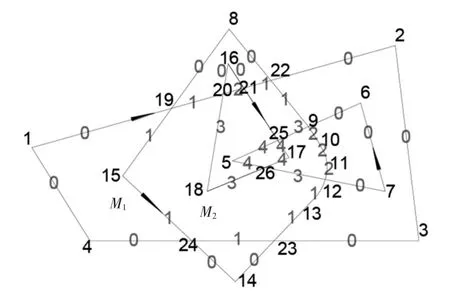
图5 线在多边形中标记示意
2.2.2 多边形差集运算
多边形线处理后,将M1中标记为1、3的线和M2中标记为0、2、4的线添加到线集合中,并对线集合进行搜索,得到环集合,将环集合构成多边域进行结果输出.根据图4的线标记结果,结合差集的选线方法得出被保留的线.M1中外部环保留的线:19-20、21-22 和 23-24,内部环保留的线:9-25和 26-12;M2中外部环保留的线:22-8、8-19、24-14、14-23、12-11、11-10 和 10-9,内部环保留的线:20-16、16-21、25-17 和 17-26.将这些线组成集合,根据线集合搜寻环,最终得到三个环:①22-8-19-20-16-21-22;②24-14-23-24;③26-12-11-10-9-25-17-26.差集结果如图6所示.
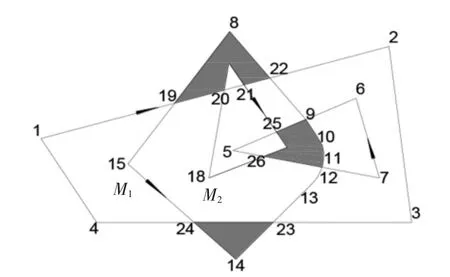
图6 M2与M1差集结果示意
2.2.3 多边形交集运算
多边形线处理后,对于M1中标记为1、3的线进行反向处理,添加到线集合.将M2中标记为1、3的线添加到线集合中,对线集合进行搜索得到环集合,将环集合构成多边域并进行结果输出,如图7所示,结果环有:①19-15-24-23-13-12-26-18-20-19;②9-22-20-25-9.

图7 多边形交集计算示意
2.2.4 多边形并集运算
多边形线处理后,将M1中标记为0、2、4的线添加到线集合中,对于M2中标记为0、2、4的线进行反向处理,再添加到线集合,对线集合进行搜索得到环集合,将环集合构成多边域并进行结果输出.从线集合中搜寻环,最终得到环:①22-8-19-1-4-24-14-23-3-2-22; ②12-11-10-9-6-7-12;③22-14-23-5-22;④20-16-21-20.将4个环组成多边形返回结果,如图8所示,结果多边形中:①为外部环,②、③、④为内部环.
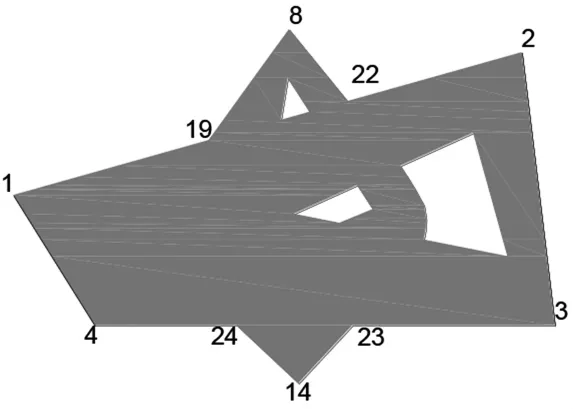
图8 多边形并集计算示意
2.3 多边形周长计算和面积计算
多边形的周长为外部环总周长与岛环总周长的和减去内部环的总周长.多边形的面积为外部环总面积与岛环总面积的和减去内部环总面积.环的面积采用计算机几何学中的矢量叉乘法计算[18].计算公式如公式(1)所示.
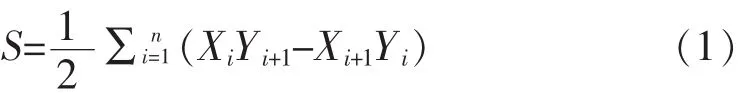
由于环P中可能含有圆弧线段、缓和曲线段,但公式(1)仅适用于由直线组成的按顺时针或逆时针存储的闭合图形的面积.故在计算环P的面积时,需将环中的全部曲线由直线替代,构成无曲线环 P1,利用公式(1)计算 P1的面积 S1.同时判断每条曲线是否在P1内部,并求解由曲线和两点连线组成的闭合图形面积.对于圆弧段部分面积,根据计算机几何学中求解弓形面积方法进行计算;对于缓和曲线段部分面积,根据缓和曲线边界的面积计算方法[22-23].计算.根据曲线是否在P1内部,对面积S1进行修改:若曲线在P1内部,则减去曲线部分面积;若曲线在P1外部,需加上曲线部分面积.当所有曲线面积处理完毕,求得面积S1为环面积.
3 实例应用
实验采用C#语言结合AutoCAD二次开发技术[23]开发CAD插件,并在主频为2.8 GHz的PC上进行实验.
3.1 运行效率测试
实验采用20组随机生成的附带缓和曲线多边形进行布尔运算同时统计运行耗时,其中20组数据根据多边形顶点数、缓和曲线线段数和嵌套层数分为5类.实验结果如表2~表4所示.

表2 差集运算运行效率实验
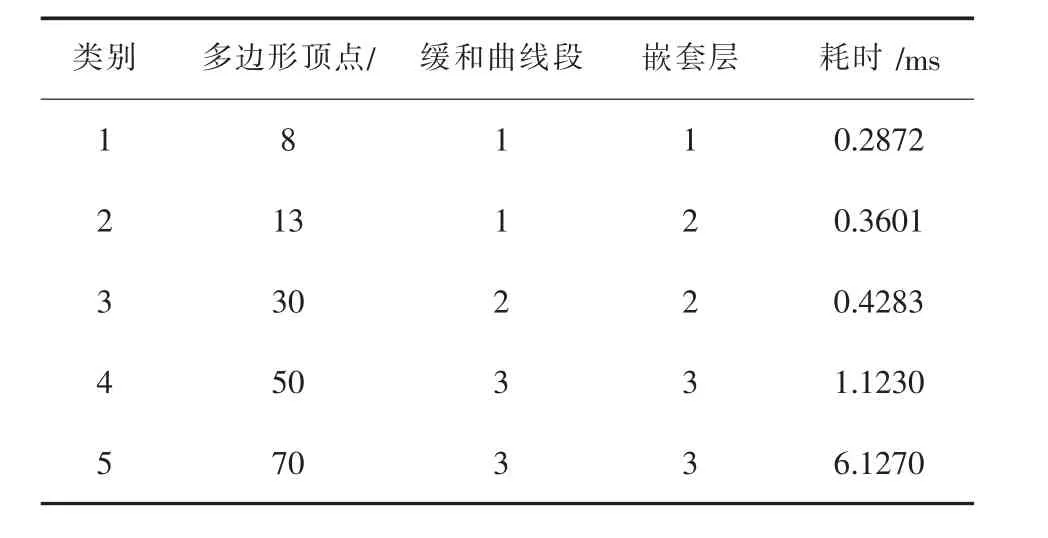
表3 交集运算运行效率实验
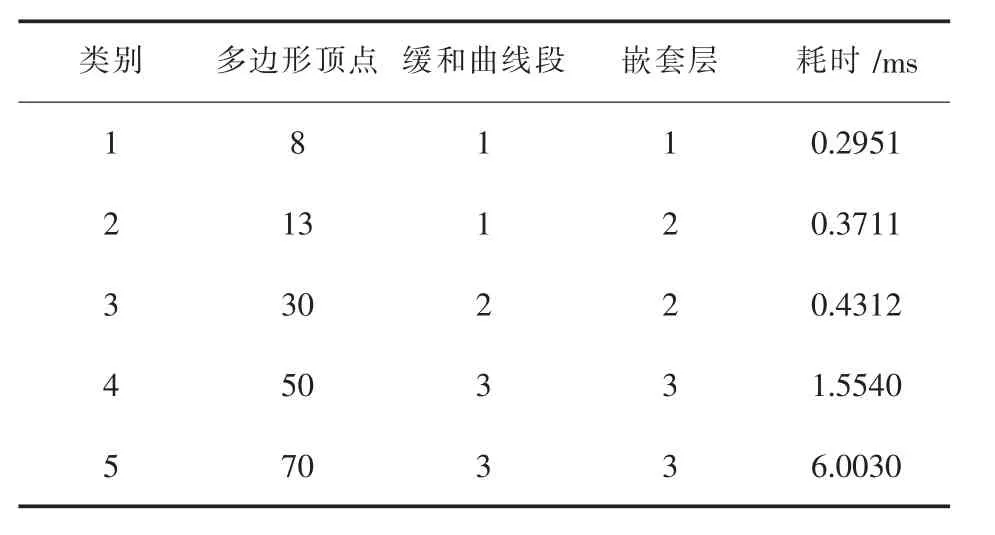
表4 并集运算运行效率实验
从理论上讲,多边形差集的处理过程比交集和并集的更简单,差集只需要将符合标记规则的线提取组合成环,并集和交集算法则需要对符合标记规则的线进行反向处理.类别1实验结果也反映了差集算法较交集和并集算法更高效.根据以上实验,随着点数增多,缓和曲线段的增加以及嵌套层的增多算法的运行效率降低.
3.2 工程实例
3.2.1 数据的来源与处理
附带缓和曲线多边形的构建与处理算法在测量工作中的许多方面都有应用,算法在江西吉安农村道路规划测量中得到了应用.数据为吉安农村道路规划测量工程图,在一段规划路中,道路缓和曲线部分经过一块含有邻村飞地(指隶属于某一行政区管辖但不与本区毗连的土地)的土地.土地实际情况如图9所示,A为该村土地,B为邻村土地,规划路经过了A与B的区域.

图9 道路规划
3.2.2 结果分析
测量工作中,要求对规划道路所占土地类型,面积等进行准确高效的统计.利用算法实现的CAD插件,选择含缓和曲线部分多边形和AB区域多边形,通过附带缓和曲线多边形交集运算,面积计算和周长计算后结果如图10所示.
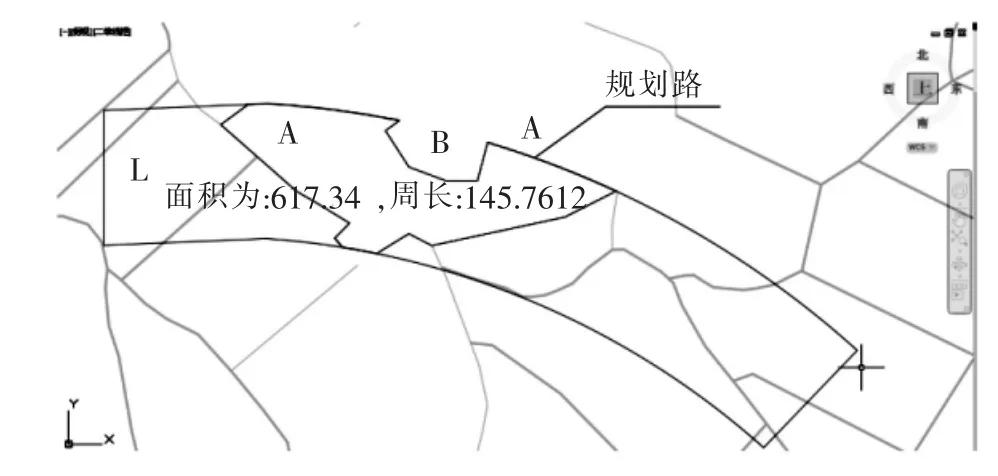
图10 交集结果
通过查询多边形属性表明算法能正确构建符合要求的多边形.交集结果图形符合逻辑和实际情况,查询交点的坐标与预期交点坐标一致,表明算法能够正确进行多边形的交集运算.对多边形交集结果的图形进行人工面积计算和周长计算.算法计算面积为617.20 m2,周长为145.74 m.与人工计算结果对比,面积误差为0.30 m2,周长误差为0.026 m,误差满足测量要求.实验表明算法能正确计算附带缓和曲线多边形面积与周长.
4 结 论
针对附带缓和曲线的多边形构建与处理,本算法根据直线段,圆弧段,缓和曲线段,多边形的几何特点进行建模,实现了附带缓和曲线多边形的模型构建,周长,面积计算和布尔运算.经过大量实验表明,该算法能正确生成附带缓和曲线多边形,能准确计算附带缓和曲线多边形的面积和周长,能实现附带缓和曲线多边形的布尔运算.该算法不仅能应用于计算机地图制图、地理信息系统、计算机辅助设计等领域,也可以为一些几何图形处理提供借鉴和启发.
