基于ℓ2，1范数的在线流特征选择算法∗

吴中华 郑 玮

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

在数据挖掘和机器学习算法研究中，对高维数据的降维是避免维数灾难［1］的重要研究手段。特征选择方法通过在原始特征集合中选择部分相关特征子集来实现降维目的。随着各种特征选择算法被相继提出，这些算法已经表明在不损失模型的预测精度的条件下，特征选择极大降低了模型所用的特征维数，进而显著提高模型的可理解性和效率［2～3］。传统的特征选择方法假设训练数据的所有特征在特征选择算法开始之前预先给定，即训练数据集的特征空间是静止且已知的。然而，现实应用领域并不一定支持这个假设条件，在现实应用中，往往由于特征提取的高代价性或者特征空间的动态性使得训练数据的全部特征在特征选择之前不一定被全部获取，从而造成特征空间是动态且未知的。例如，高分辨率行星图像上的火星陨石坑检测是行星研究中一项很重要的任务，陨石坑计数提供了测量行星表面相对年龄的有效方法。提取纹理特征用于陨石坑检测已经被证明是实现自动陨石坑检测有效的途径之一［4～5］。因高昂的特征抽取代价和抽取多大规模的纹理特征集合是未知的，从覆盖火星表面的行星图像上预先生成所需要的纹理特征集合几乎是不可行的。

特征空间随时间变化而变化的动态特征空间被定义为流特征。流特征概念下的特征选择过程中，因预先没有给定整个特征空间知识，局限于静态特征空间的传统特征选择方法已经不能够满足这种场景下的特征选择要求。因此，新的基于流特征概念下的特征选择方法被提出来处理特征空间是动态且未知的条件下的特征选择问题［6］。由此，流特征选择问题被定义为样本空间不变的条件下，特征空间维度随时间而增加，且每个新流入的特征被立即在线处理而不需要预先获得训练数据的整个特征空间的先验信息。这样，把动态、未知条件下的特征选择问题转化为流特征概念下的在线特征选择问题。目前已有相关研究来解决流特征选择问题，Perkins 等提出一种基于逐步梯度下降的流特征选择框架，使用ℓ1范数作为约束条件提出Grafting 算法［6］。这个算法后来被Glocer 等用于图像处理中的边的在线侦测问题［7］。Zhou 等提出一种基于逐步回归的在线特征选择算法：Alpha-investing 算法［8～9］，该算法需要知道候选特征构成的先验知识，然后根据先验知识对初始特征进行变换。Wu 等根据对特征子集的四种定义：不相关特征［10］，冗余特征，非冗余特征［11］和强相关特征，提出OSFS（Online Streaming Feature Selection）算法［12］选择出动态流特征环境下的非冗余特征和强相关特征。算法利用统计检验的方法检测特征与标签，特征与特征直接的相关性。在大数据的应用中，特征选择技术是非常重要的，Wu 等在osfs 算法基础上提出了SAOLA（Scalable and Accurate OnLine Approach）算法［13］，一种可扩展和准确的在线选择方法。但是由于算法采用基于统计量判断的Filter特征选择方法带来的局限性，以及为加快运行速度而仅仅采用成对对比的判断策略，使得saola 算法在分类任务上没有明显优势。Jundong Li等将流特征选择算法应用于社交媒体的特征选择问题中，提出一种无监督的流特征选择算法：USFS（Unsupervised Streaming Feature Selection）算法［14］。社交媒体数据增长迅速，数据的特征空间以动态未知的情形增长，传统的静态特征选择算法不适用在这种场景下。同时社交媒体数据多为无标签信息的数据，文献［14］通过提取用户链接关系中的社交潜在因素信息作为流特征选择算法的约束条件，提出社交媒体的无监督流特征特征选择算法。

相较于ℓ0范数和ℓ1范数易受噪声干扰的缺点，ℓ2，1范数对噪声不敏感，同时具有行稀疏性质，适用于约束结构化稀疏问题。目前已有关于ℓ2，1范数应用于传统静态特征选择作为约束条件的研究［15～17］，此类算法通过对特征选择矩阵进行ℓ2，1范数最小化约束来选择特征。为解决在线流特征选择问题，本文提出了新的基于ℓ2，1范数约束条件下的流特征选择模型及流特征场景下的优化算法。

2 流特征选择模型

对于一个流特征空间数据集，定义每一个样本向量xi的类别为，若xi属于第k 类，则yi，k=1，其余值为0，类别标签矩阵为，其中n 为样本数，c 为类别数。设流特征空间在t时刻流入数据空间的样本数据为，此时的特征权重矩阵为。

定义t时刻的特征选择损失函数为

为简便起见，偏置项bt被添加进入Wt矩阵，同时在数据矩阵Xt中增加全1 列向量。由此损失函数变成：

这里，损失函数为样本权重积与类别的最小残差平方和模型，即预测值与实际值残差的Frobenius范数。增加对特征权重矩阵Wt的正则化约束R(Wt)和系数λ以避免模型过拟合，目标函数为

本文使用ℓ2，1范数作为约束条件，目标函数可重写为

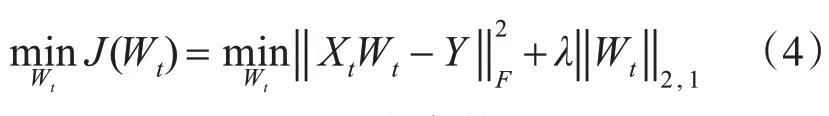
式（4）中：λ是一个权衡参数；‖ ⋅ ‖2，1表示ℓ2，1范数，ℓ2，1范数正则化能控制权重矩阵Wt的数据尺度并同时保证Wt的行稀疏性，使得模型能够选择出最优的特征子集。

3 流特征选择算法

3.1 接收新特征

流特征环境下，每个特征逐个到达并即刻在线处理，完整的特征空间预先不可知，特征空间动态变化。设在t 时刻新到达特征，其特征权重向量，此时的特征空间为，特征权重矩阵为这里，新特征ft是特征空间Xt的第t 列，权重向量wt是权重矩阵的Wt的第行。若新添加的特征ft使得目标函数取得最优值时，其特征权重向量wt=0，即新特征ft的加入对于模型的优化没有起到作用，此时拒绝并丢弃新特征ft；否则，新特征ft接收进入模型。因此可以通过判断目标函数J(Wt)是否在坐标原点取得最优值来判断是否接收新特征ft。

因ℓ2，1范数在原点处不可导，故目标函数在原点处亦不可导，但是目标函数在原点处的任意方向梯度均存在。若原点为目标函数极值点，则目标函数在原点处的任意方向的方向导数均为正数。此时，在非常接近原点处的任一方向取得采样点

使用点ω的方向导数代表原点处目标函数的方向导数。有：

因此，若对于原点领域内任意采样点，式（5）均满足，则拒绝新特征ft。否则，只要存在一个采用点不满足式（5），则接收新特征。理论上，ε值越小，目标函数在采样点ω处的方向导数越接近原点处的方向导数。但随类别数c 的增加，目标函数空间维度增加，使得高维空间累计误差增加，所以ε在目标函数维度过高时不宜过小。

式（5）可约简为

此时拒绝新流入的特征ft。由此，新特征ft被接收的条件为其权重向量wt满足：

采样策略为高维空间的超球面上均匀采样。为方便计算，可以在高维空间的超立方体表面均匀采样。

接下来根据矩阵的求导法则，求出目标函数对新到达特征的权重向量wt的梯度。对目标函数做恒等变换：

这里，ℓ2，1范数在原点处不光滑，借助辅助矩阵D转化为一个次梯度的形式。D是一个对角矩阵，对角线上的值为

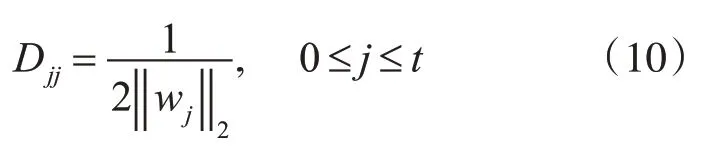
利用范数和矩阵迹的求导公式可得损失函数对于特征向量wt的梯度为

这样可以得到目标函数对新特征权重向量的导数为

可得到针对本文提出的特征选择模型在t时刻到达的新特征ft接收条件为其权重向量wt满足：

3.2 更新模型

通过接收条件检测的新特征即表明这个特征是一个对模型有用的特征，则接收新特征进入模型。在每次新接收一个特征之后，重新对模型进行整体优化，更新所有已接收特征的权重。本文使用共轭梯度法（conjugate gradient algorithm）优化模型［18］，因为其收敛速度快速，计算开销低。

若在t 时刻，新特征ft被接收，新增的特征可能会使得已接收的最优特征子集中存在冗余特征，即新特征的接收造成已选特征的冗余，或者新特征虽然通过接收条件的检测，但新特征对于已接收最优特征子集是冗余的，此时需要去除冗余特征。每次接收新特征之后，重新对模型做一次整体优化，因新特征的加入，冗余特征的权重向量会变为0 向量。去除权重向量ℓ1范数趋近于0 的特征，即可去除冗余特征。

3.3 算法框架

根据上述理论推导，将算法框架描述如下。算法1 描述完整的流特征选择算法总体框架。当t时刻新特征ft到达，若新特征通过梯度测试，则接收新特征ft进入当前最优特征子集BFSt，使用共轭梯度法更新当前最优特征子集的权重向量并删除冗余特征。

算法1 流特征选择算法

输入：X，Y，λ，ε

输出：t时刻的最优特征子集BFSt

1）Initial：BFSt=，Wt=1

2）Wt=update_weigh（tWt，BFSt，Y，λ）

3）While not convergence：

4）//在t时刻，新特征ft到达

5）ft=get_new_feature（）

6）//检测新特征是否通过梯度检测

7） If gradient_validation（ft，Wt-1，BFSt-1，Y，λ，ε）：

8）//新特征通过梯度测试，接收进入模型并更新模型

9）BFSt=[BFSt-1，ft]

10）Wt=update_weigh（tWt，BFSt，Y，λ）

11）//去除冗余特征

12）Wt，Xt=refresh_selected（Wt，Wt）

13） End if

14）End while

15）//返回收敛后的最优特征子集

16）ReturnBFSt

算法1中的梯度检验算法如算法2描述。根据接收新特征的条件，若存在某一方向，使得目标函数J(Wt)满足式（13），则返回真，新特征通过梯度测试条件。否则，返回假，新特征未通过接受条件。

算法2 梯度检验（gradient validation）

输入：ft，Wt-1，BFSt-1，Y，λ，ε

输出：布尔值，是否通过梯度验证

1）Initial：BFSt=[BFSt-1，ft]

2）//产生多个采样方向

3）sample_directions=generate_sample_directions（ε）

4）//判断是否存在一个方向使得接收条件满足

5）for direction in sample_directions：

6）//计算目标函数在采样方向的导数

7） grad=derivative（direction，J，BFSt，Y，λ）

8） If grad*direction＜0：

9） Return True

10）//所有采样方向均不满足接收条件，未通过检测

11）Return False

4 实验分析

为了验证提出的流特征选择算法效果，在多个数据集上进行了实验，使用多个高维数据集模拟流特征环境下的特征选择问题。为将本文的算法与现有流特征选择算法做比较，使用sklearn 科学工具包中的线性svm分类器对算法进行5折交叉验证方法，平均分类精度和选择的特征数量作为评价算法性能的两种标准。

4.1 数据集

实验中使用12 个数据集来验证本文提出的流特征选择算法。数据集全部来自于亚利桑那州立大学（Arizona State University）的特征选择数据库。其中序号为1～3 的是人脸图像数据集，序号为4～9的是生物信息数据集，序号为10 的是来自于NIP2003 特征选择挑战比赛数据集，序号为11～12的是文本数据集。所有数据集的描述在表1给出。

表1 实验中使用的数据集

4.2 数据预处理

为保持所有的特征在相似的尺度标准中，对每一个特征进行归一化到标准正态分布的处理。在特征选择之前，将特征重新调节为标准正态分布。对于特征f，标准化之后的特征为

4.3 对比实验

为评估本文提出的算法的有效性，与现有流特征选择算法进行了多个数据集的对比实验。图1显示了本文提出的算法与现有算法的对比实验结果。实验中使用的对比算法均来自于LOFS提供的在线流特征选择算法［19］。根据算法库的使用手册设置了实验中算法的最优参数。sfs_l21 为本文提出的算法，算法引入了两个参数λ和ε。通过参数调优，对于实验中参数进行了最优设置。实验结果对比图中下半部分表示不同算法选择出的特征个数，选择的特征个数越少，表明算法的压缩性能越好。上半部分表示在对应压缩率情况下的分类识别率率，识别率越高表明算法的识别性能越好。

4.3.1 与grafting算法实验结果对比

图1 描述与grafting 算法相比较的结果。可以看出，本文提出的算法在所有数据集上均得到了更高的分类识别率。在其中的6 个数据集上选择了更少的特征，同时保持更高的分类识别率。在12个数据集中的10 个数据集选择出了同数量级的特征个数，但是却得到明显优于grafting 算法的分类识别率。文本数据集的最优特征子集规模比较大，在两个文本数据集上，本文的算法选择出的特征个数较高，能得到更好的分类识别率。得出结论，本文提出的算法在保持相近的压缩率的同时，在分类识别率上明显优于grafting算法。

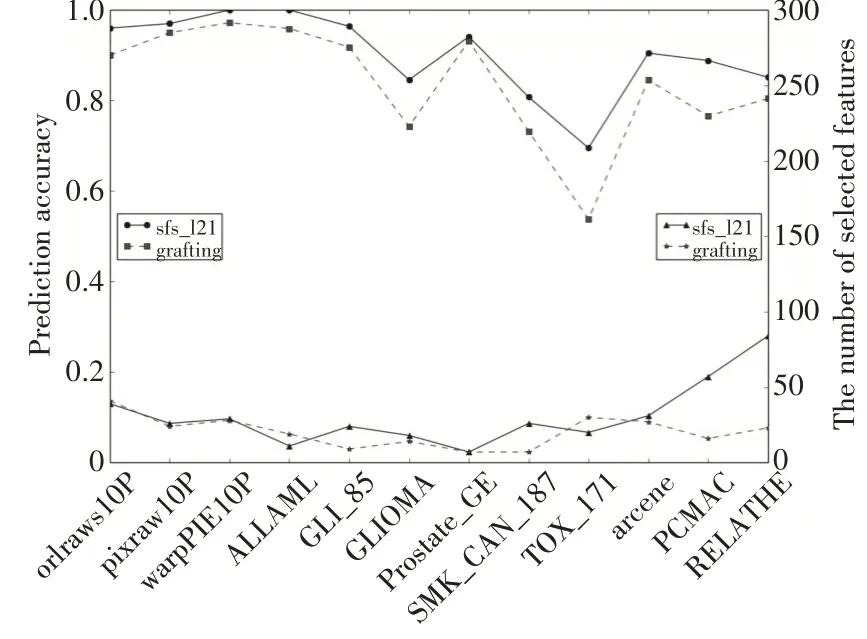
图1 与grafting算法实验结果对比

4.3.2 与osfs算法实验结果对比

对比实验中osfs算法为fast版本：fast_osfs在alpha=0.01 下的结果。osfs 算法的fast 版本不会降低选择的特征的质量，同时能加速算法的运行。图2与osfs算法相比较可以看出，本文提出的算法在10个数据集上的识别率都要高于osfs算法。osfs算法运行复杂度随选择的特征个数成指数增长，为了提高算法效率的考虑，总是选择出最少的特征，这样不可避免地会去除掉好的特征。本文提出的算法虽然压缩率比osfs 算法稍差，但是在分类识别率方面明显优于osfs算法。

图2 与osfs算法实验结果对比

4.3.3 与Alpha_investing算法实验结果对比

图3 与Alpha_investing 算法相比较，本文提出的算法在11 个数据集上得到更高的分类正确率，在另外1 个数据集上选出更少的特征个数，得到了相近的分类精度。本文提出的算法与Alpha_investing 算法对比，具有相近的压缩率，同时具有更好的分类识别率。

图3 与Alpha_investing算法实验结果对比

4.3.4 与saola算法实验结果对比

实验中的saola算法参数alpha可取的值为0.01或0.05，alpha 值的选择不会明显的影响算法的结果。为了对比结果的方便，实验中设置alpha=0.01。图4 与saola 算法相比较，本文提出的算法在11 个数据集上得到的更好的分类精度。可以看出，在多数数据集上本文提出的算法识别性能更优，能得到更好的分类精度。同时在压缩率上没有明显的劣势，与saola算法大致持平。

与grafting，osfs，Alpha_investing 和saola 算法对比，可以得出结论，本文提出的sfs_l21 算法在压缩率较低的情况下，识别率达到了较高的水平，在多数数据集上能得到最优的分类识别率。

图4 与saola算法实验结果对比

4.4 未知特征空间下的流特征选择结果分析

在上述实验中，使用的是已知特征空的数据集来验证流特征选择算法的实验结果。为进一步研究流特征选择算法在未知特征空间的情况下的算法性能，使用分类精度为标准来研究流特征选择过程中算法的稳定性。实验中选择了6 个数据集，pixraw10P，TOX_171，SMK_CAN_187，Prostate_GE，arcene 和PCMAC 作为实验数据集。同样使用sklearn工具包中的线性svm算法做5折交叉验证的平均分类精度作为评价标准。

从图5 中可以看出，在特征逐个流入的过程中，本文提出的算法在pixraw10P，SMK_CAN_187和PCMAC 数据集上，当特征流入数据空间的比例到达50%之后，分类识别度都保持在所有算法中的最高水平。在arcene和Prostate_GE数据集上面，数据空间到达30%之后，分类识别率就已经高于其他算法。在TOX_171 数据集上也会在数据空间达到60%之后保持较高的分类识别率。由此可见，本文提出的算法不需要预先获得整个特征空间的全部信息就可以达到最优分类精度，6 个数据集上均能持续保持较高的分类识别精度。

图5 分类进度随着特征数量的不断流入而变化

可以得出结论，相比与grafting，osfs，Alpha_investing 和saola 算法，在未知空间的流特征选择中，本文提出的算法在模型预测精度方面获得了更高的和更稳定的性能。

4.5 参数分析

算法中引入两个参数λ和ε，λ与特征选择模型相关，ε控制选择特征个数来间接影响分类精度，两个参数相互独立，互不干扰。通过固定其中一个参数值，考察另一个参数对分类精度的影响的方法来分析参数对算法影响。

4.5.1ε的影响分析

实验中固定参数λ=0.2，考察ε在0.01～0.20范围内变化对数据集SMK_CAN_171，GLIOMA，Prostate_GE 和arcene 选择特征个数和分类识别率的影响。

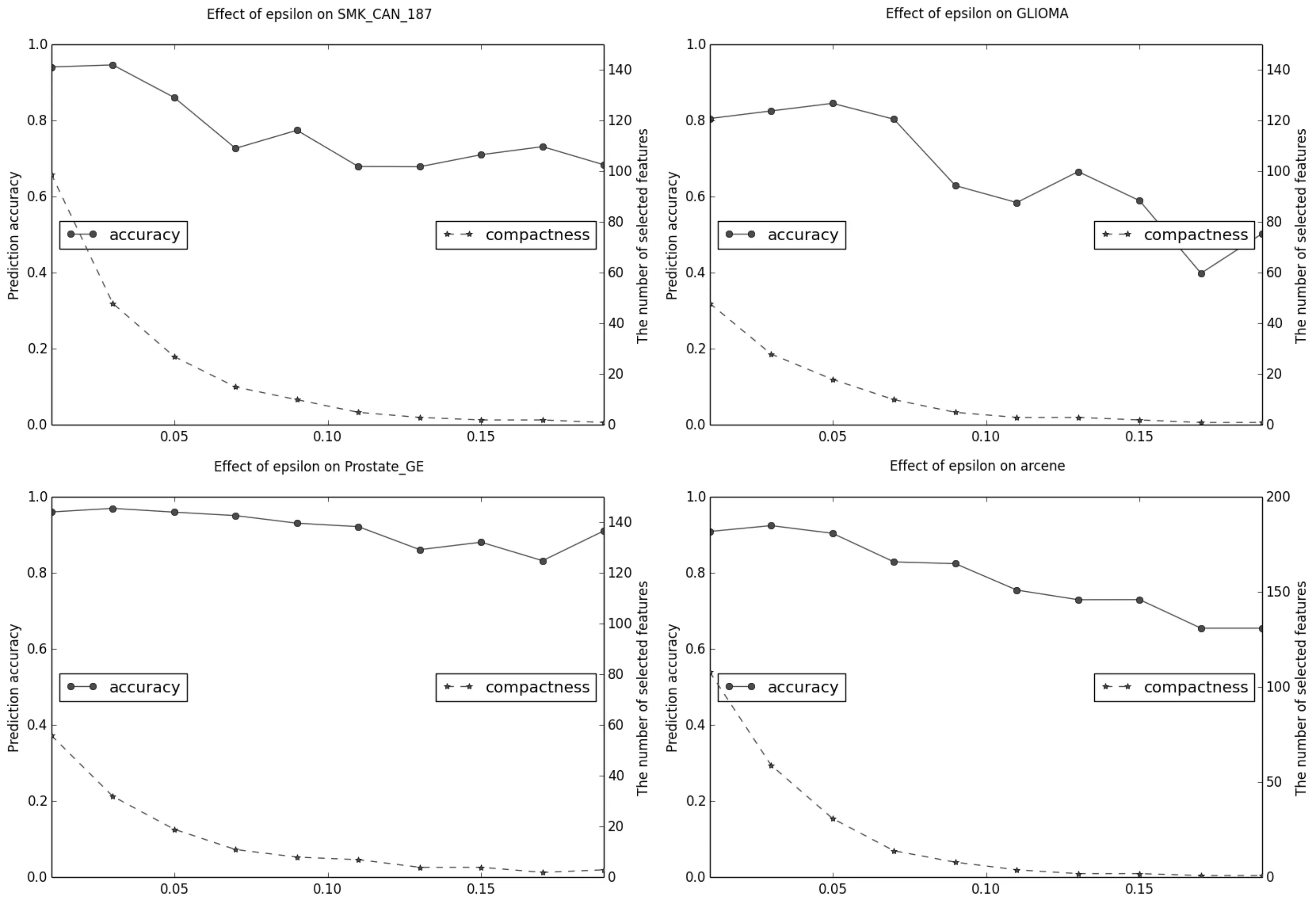
图6 参数ε 对4个数据集影响

图7 参数λ 对4个数据集的影响

图6 描述了随ε值的增加，选择的特征个数明显减少，分类精度有下降的趋势。可以看出，ε的选择对选择的特征个数和分类正确率是敏感的，对选择特征个数敏感度较高。ε的经验值设置为ε=0.05，此时分类精度和选择特征个数可以达到一个权衡。ε对算法的影响受数据集的最优特征子集的规模大小影响较大。ε设置越小，选择出的特征子集规模越大。

4.5.2λ的影响分析

实验中，固定参数ε=0.05，考察λ在0.1～0.5范围内数据集SMK_CAN_171，GLIOMA，Prostate_GE 和arcene 选择特征个数和分类识别率的影响。

从图7 可以看出，λ值的改变对数据集分类正确率和选择特征个数影响较小，在4 个数据集上选择出的特征个数和分类精度变化幅度较小，对算法的影响敏感度较低。

5 结语

针对流特征场景下的在线特征选择问题，本文提出了基于ℓ2，1约束的流特征选择算法，可以有效地解决流特征下的在线特征选择问题。通过对比实验分析，本文提出的算法比现有流特征选择算法在基因表达数据集上能选出更优的特征子集，使得分类精度较高，同时选择的特征个数适中。实验中分析了参数对算法的影响，算法对λ的敏感度较低，对ε的敏感度较高，ε可以显著地影响选择的特征数量，进而间接影响分类正确率。本文提出的流特征选择算法能较好解决流特征场景下的特征选择问题，在动态的、未知的特征空间中选择出更优的特征子集。