城市密集人群疏散算法设计研究∗
2019-07-10莫乐群
莫乐群
(广东交通职业技术学院 广州 510650)
1 引言
随着社会经济发展,公共场所高度集约化和规模化建设给公共安全带来重大隐患,一旦发生事故容易造成群死群伤事件。如何在最短时间内有效疏散密集人群,让人群组织有目的、有计划逃离事故现场,是目前公共安全研究的重点和难点。
行人遭遇突发事件过度恐慌,出于逃生本能会出现推搡、踩踏等事件[1~3]。受疏散群体影响以及个体心理和生理差异,个体行为表现出一定的趋众性和不确定性,因此行人流是一种极其复杂而又特殊的非线性物理运动。传统宏观行人流建模中把疏散速度与行人之间影响看成线性关系并不适宜[4~5]。微观行人流建模有社会作用力模型、磁场引力模型、格子气模型、元胞自动机模型等。其中元胞自动机模型将疏散个体描述为元胞,通过不同元胞相互作用和动态演化模拟人的个体行为和群体效应,目前已被广泛应用于行人流理论和疏散建模研究。
元胞自动机模型由元胞、元胞空间、邻居和演变规则四部分组成。其中,演化规则是行人流建模的核心,对人群疏散模拟有重大影响,直接决定疏散效率和人员伤亡情况。由于元胞状态更新策略由元胞自身位置和邻居元胞状态共同决定[6~7],这与粒子群PSO 算法中鸟类寻找全局最优值思想一致[8~9]。文章将元胞状态更新转变为策略优化问题,通过求解适应值函数计算元胞全局最优演化规则,从而提高疏散效率,减少人员伤亡的目的。
2 元胞自动机模型
元胞自动机模型是一种时空离散的动力演化系统。网格中每一个元胞选取有限离散状态,并遵循相同演化规则更新当前状态[10]。所有元胞根据自身和周围元胞状态相互作用[11~12],共同构成动态系统演化。元胞自动机模型由元胞、元胞空间、邻居和演变规则四部分组成[13~15]。定义元胞集合S:S={0,1,2,…,k-1},其中元胞邻居半径为r,则在t时刻,位置(i,j)的状态记为,见图1。

图1 元胞位置示意图
对于Neumann邻居,邻居关系定义为

对于Moore邻居,邻居关系定义为

定义cit为t 时刻位于i 处的元胞,局部演化规则函数f和全局演化规则F,之间关系如下:

全局演化规则是所有局部演化规则的集合,元胞每一次演化都对周围元胞产生影响,促使所有元胞同步更新位置和状态,模拟疏散人员复杂行为过程。
3 粒子群模型
粒子群PSO 算法是基于鸟类群体觅食行为的演化算法。搜索空间中的每只鸟对应全局的每个解,每个粒子根据邻居粒子寻找的最优信息改变自身位置和飞行状态,迭代找到全局最优解。目前粒子群算法已广泛应用与求解离散优化问题,实现步骤如下:

在n个粒子群组成的d维密闭搜索空间,第i个粒子位置为xi=(xi1,xi2,…,xid),速率为vi=(vi1,vi2,…,vid)t。每个粒子以寻找邻居全局最优解为目标更新自身飞行速率和位置状态:其中,c1和c2是学习因子,k为迭代次数,W 为惯性权重,rand是[0,1]区间平均分布的随机数,表示粒子在第d 维空间速率,是第i 个粒子经k 次迭代后的极值,是粒子群全局极值,和分别是粒子i经k次迭代后的第d维位置和速率。
每个粒子通过搜索邻居最优解更新自身位置和速率,迭代找到全局最优解,完成搜索过程。
4 新算法实现方法
4.1 基于粒子群优化的元胞更新规则
在元胞自动机模型中,元胞状态更新策略由元胞自身位置和邻居元胞状态共同决定,这与粒子群鸟类寻优思想一致。文章将元胞状态更新转变为策略优化问题,通过粒子群算法求解元胞迁移概率最优化形成适应值函数fitness,形成元胞最优演化规则,从而提高疏散效率,减少人员伤亡的目的,算法流程如下:
1)初始化元胞空间大小为M*M 网格,元胞粒子个数为N,速率为

其中vmin和vmax表示元胞粒子速率的上下限。
2)计算元胞粒子适应度值fitness(Pi),计算第i个粒子极值为

粒子群全局极值为

3)利用粒子群更新元胞当前状态

其中,h满足关系如下:

4)更新元胞离子极值
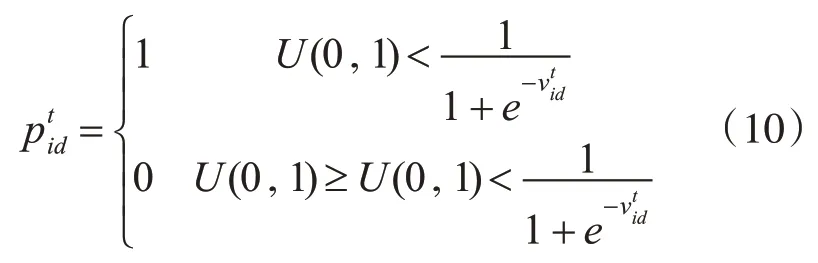
6)计算全局最优演变规则fitness(gb)=max
4.2 元胞自动机模型设计
将元胞自动机空间网格划分为分成0.3m×03m网格,大小为拥挤时人所占据的平均空间。在t时刻,dv(t)用来表示行人与出口v之间距离,则有:
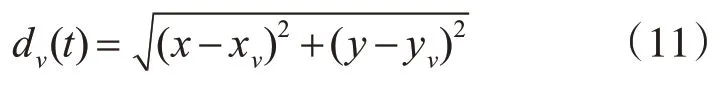
其中,(x,y)表示t时刻行人位置,(xv,yv)表示出口的位置。
定义densityv(t)为出口v的人员密度,则有:

其中,n表示出口区域Sv行人总数。A 为Sv区域内元胞个数。
4.3 粒子群优化元胞迁移概率
若考虑行人与出口之间距离d对元胞迁移的影响,则元胞在t时刻选择下一网格r迁移的概率为

若考虑Sv区域行人密度对元胞迁移的影响,则元胞在t时刻选择下一网格u迁移的概率为

综合上述两种因素,元胞迁移概率为

利用粒子群算法计算元胞迁移概率参数α和β的最优组合,形成局部演变规则fitness(pbi),过程见式(7)~(10)。
4.4 疏散路径成本计算
为提高疏散效率,应使疏散时间Tmin最小。设(xi,y)i为疏散人员i初始坐标,最优逃生路径长度为
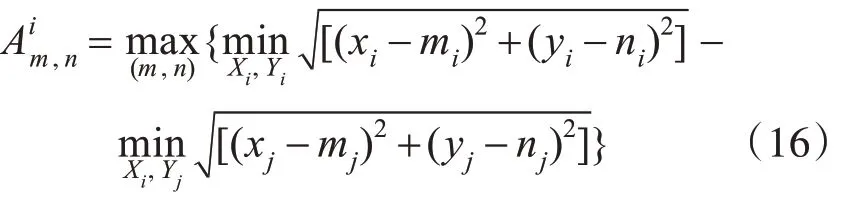
5 仿真测试
5.1 测试环境
仿真实验选取某市火车站站厅,共7 大出入口,其中,出入口⑦是站厅进门,其余出入口是换乘出口,★代表突发事件地点,见图2。初始化元胞空间5000*2500 网格,每个网格空间为0.3m×03m,疏散人群1000 人,采用随机分布方式。粒子群惯性权重Wmax=0.9,Wmin=0.3,算法在各个出口疏散效率见图3。
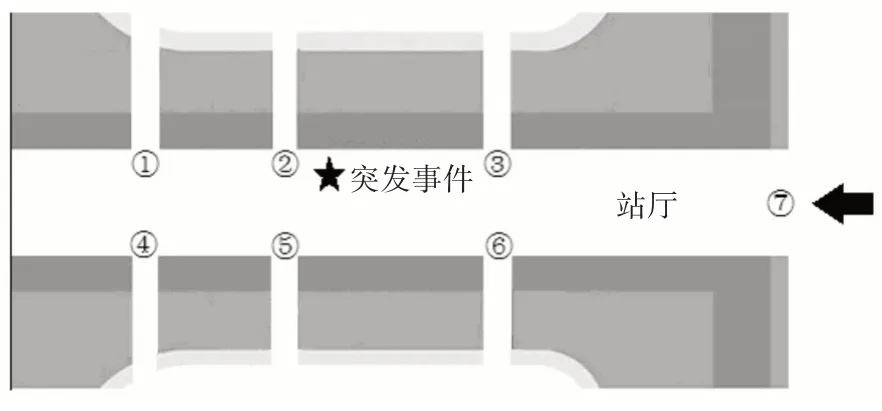
图2 仿真实验拓扑图
5.2 测试结果
从图3 可以看出,各个出口疏散效率有较大差异,其中出口⑦疏散效率最高,在相同时间疏散近1/4 人群,究其原因,首先,出口⑦所占网格空间较大,经粒子群求解最优适应度函数致使其通向出口⑦的元胞迁移概率较高;其次,受行人对陌生环境和趋众心理影响,习惯按进门方向折路返回。而出口②疏散效率最低,因为其距离突发事件较近,行人受趋利避害效应逃亡其他出口,这与实际情况相符。
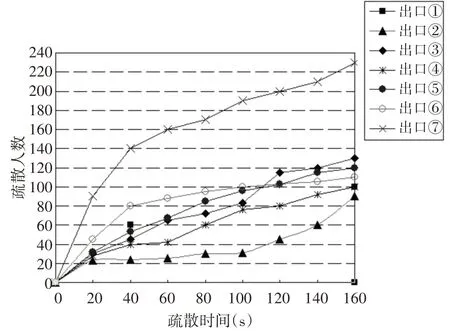
图3 各出口疏散效率对比图
6 结语
文章将元胞状态更新转变为策略优化问题,通过粒子群算法求解元胞迁移概率最优化适应值函数,形成元胞最优演化规则,从而提高疏散效率,减少人员伤亡,对密集人群场所疏散演练和检验建筑设计合理性等具有重要现实意义。
