测量不确定度分析在大学物理实验设计中的应用

樊代和 贾欣燕 刘其军 常相辉 魏 云

(西南交通大学物理科学与技术学院；物理国家级实验教学示范中心，四川 成都 611756)

1 提出问题

大学物理实验是一门培养本科生动手能力和科学实验素养的重要实践课程之一[1]。目前，国内大部分高校，包括西南交通大学开设的传统基础型物理实验项目，在实验教材中都明确了“实验目的”“实验仪器”“实验原理”“实验步骤”等几部分内容[2]。高校本科生在进行大学物理实验课程内容的学习过程中，一般在课前要预习教材中的“实验原理”部分并写出预习报告，在实验课时听取教师对具体实验原理的重难点和实验注意事项等内容的介绍，然后按照教材所列出的“实验步骤”内容逐一进行测量，就可较好地完成该实验项目所需的测量。在没有测量错误的情况下，最终都可以得到较为理想的实验测量结果。

然而，这种传统的实验教学内容和教学方法，实际上是极度缺乏创新理念的[3]，对培养本科生的创新能力无法提供进一步的帮助。具体而言，本科生在完成某一实验项目后，只能对本实验项目所采用的测量原理，以及所获得的测量结果有一定的了解，但一般不会去积极思考该实验项目为什么要采用这样的实验方法和实验仪器？应该采用何种实验原理，或者采用何种实验仪器对该实验项目进行改进就能得到更为精确的测量结果等问题。大部分本科生在修完大学物理实验课程后，只能了解到从这门课学到了什么，而不能了解到这门课为什么学，如何才能学好的问题。

西南交通大学物理实验中心(以下简称实验中心)所开设的大学物理实验课程，在学期开始的第一次实验课时，就专门用6学时的课时对本科生讲解测量不确定度的相关知识。该部分教学的目的是为了使本科生能够全面了解测量不确定度在物理实验中所起的重要作用。然而，在实际的实验教学过程中发现，大部分学生对测量不确定度的学习和应用仅仅停留在用其进行物理量测量结果的不确定度评定方面，不会去主动思考不确定度分析在物理实验内容设计过程中所起的重要作用，就更谈不上能够对现有实验仪器进行改进了。换言之，通过大学物理实验这门重要的实践课程的学习，对学生创新能力的培养还没有达到预期的目标。

为了克服以上提到的问题，实验中心除了进行如上所述的6学时的测量不确定度知识讲授外，还增加了一个设计性实验项目，如“单摆的研究”，用于加强本科生对测量不确定度知识的全面掌握。但经过一定时间的教学实践发现，仅用一个设计性实验项目来进行测量不确定度分析的学习还不够。因此，在最近几年里，实验中心在所开设的所有基础性物理实验教学内容中，特别地引入了测量不确定度分析相关知识在具体实验内容中所起作用的讲授工作。通过实践发现，这样的教学内容改革，不但可以让本科生能够更加深入地掌握所学的实验内容，而且能够根据所学的测量不确定度相关知识，提出针对具体实验内容的改进方案。通过将测量不确定度分析应用到高校大学物理实验课程的基础性实验项目内容中，能够对学生进行创新性思维的启发，进一步为高校培养创新性人才奠定坚实的基础。

本文以目前实验中心所开设的3个具体实验项目，如“单摆的研究”“杨氏弹性模量测量”“分光计测量三棱镜折射率”等为例，对测量不确定度分析在具体实验内容设计中的应用以及所取得的成果进行介绍。

2 不确定度分析在实验设计中的应用举例

众所周知，单摆实验是测量重力加速度g的一种实验方法，有部分本科生在中学阶段就接触过此实验[4]。然而，我们在大学物理实验的实际授课过程中发现，学生对该实验项目了解的仅是之前中学教师讲解的初步知识内容，如：为了测量重力加速度g的值，在单摆小角度摆动情况下，只需要将单摆摆动n个周期所用的总时间t测量出来，然后计算得到单摆的摆动周期T=t/n，最后利用测量得到摆长L的值，利用公式，

(1)

就可以得到重力加速度g的值。

但是，这里有一个重要的物理问题学生们并没有进行思考。如为什么采用单摆来测量重力加速度，而不采用“自由落体法”[5]进行测量？假设采用单摆法进行测量，实验仪器涉及的实验参数(例如摆长L的选取，以及测量周期时所涉及的n取值的选取)应该如何设定，才能将测量重力加速度g的相对不确定度控制在0.5%以内？换句话说，这个实验该如何设计，才能满足仪器设计时所考虑的测量精度的要求，学生之前很少有思考过的。为此，实验中心就专门开设了一个设计性实验项目，名称为“单摆的研究”，用以说明测量不确定度分析在实验内容涉及方面所起的重要作用。该实验项目的具体内容和说明如下：

首先，根据式(1)，可以计算得到重力加速度g的相对不确定度的表达式如下所示：

(2)

其中，uL和uT分别为摆长和周期的不确定度。为了满足测量精度要求ug/g≤0.5%，利用不确定度的等量分配原则，可将式(2)中的两个物理测量量(长度和时间)进行分离变量操作，即

这样，结合公式t=nT，在只考虑B类不确定度的情况下(设计实验时还没有进行多次测量，因此可暂不考虑A类不确定度)，直接就可以得到

从式(4)中可以看出，只要在实验前估计出测量摆长时可能的所有误差ΔLi以及测量时间时可能的所有误差Δti，即可得出满足设计要求下，单摆装置需要设置的最小摆长Lmin及所需测量的最小摆动次数值nmin。或只要单摆实验项目中的所涉及到的摆长和摆动次数能够满足式(4)，那任何一个学生采用这样的实验仪器，在实际实验测量时，即能得到满足设计要求ug/g≤0.5%的实验测量结果。当然，一方面，由于实际实验测量中，要考虑重复测量的A类不确定度，因此实验仪器中摆长和摆动次数可再适当放大一点；另一方面，为了尽可能方便地满足式(4)，可对学生选择不同的测量仪器(不同的测量仪器选取将对应不用的B类不确定度)提供依据。

以上即为实验中心所开设的一个设计性实验，用于培养学生利用所学的不确定度知识来设计一个简单的，满足实验设计要求的一个具体实验项目步骤。在实际的教学过程中，我们发现通过开设类似的设计性实验项目内容，可进一步培养学生的创新思维能力，为其进一步将测量不确定度知识应用到其他物理量的精确测量过程中提供参考。

例如，杨氏弹性模量实验[6]也是目前大多数高校所开设的一个实验项目，该实验项目的目的一方面是让同学们掌握一种测量杨氏弹性模量，包括光杠杆测量微小伸长量的方法；另一方面大多数高校也要求进行详细的不确定度计算，用以对不确定度相关知识的进一步掌握。目前大多数高校该实验仪器中采用的钢丝原长L约在400mm到800mm之间。在实际的实验过程中，如此长的钢丝原长就可能会使钢丝有一定的自然弯曲，导致钢丝原长的测量存在较大的误差。因此，有部分积极思考的同学就会提出如下的问题：在杨氏弹性模量测量仪中，能否将钢丝原长L设置得更短一些呢？简单地回答此问题，钢丝原长L缩短，则会导致在单位拉力下，钢丝的微小伸长量ΔL将更小，不利于实际的实验测量。但此问题可通过增加光杠杆到望远镜的距离D来克服。为何要取这么长的钢丝原长呢？事实上我们也可从测量不确定度的知识方面来回答此问题。

根据杨氏弹性模量E的计算表达式，

(5)

其中，F为待测金属丝沿长度方向所受外力；D为光杠杆到望远镜的距离；L为钢丝原长；b为光杠杆的长度；d为钢丝直径；ΔN为望远镜中标尺两次读数的变化量。可计算得到，其相对不确定度表达式为

(6)

其中，xi={F,D,L,b,d,ΔN}；uxi为对应的不确定度。当选取一般实验情况下的参数值，例如F=10N，uF=0，D=1000mm，uD=3mm，b=70mm，ub=0.3mm，d=0.7mm，ud=0.002mm，ΔN=3mm，uΔN=0.1mm，uL=1.0mm，可以得到杨氏模量的相对不确定度uE/E随钢丝原长L的变化关系如图1所示。

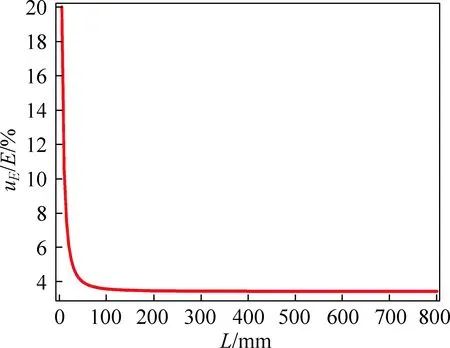
图1 杨氏模量相对不确定度随钢丝原长的变化关系曲线

从图1中可以看出，随着选取钢丝原长L值的增大，测量钢丝杨氏弹性模量的相对不确定度将减小。特别地，当L<100mm时，相对不确定度值随L的增大将急剧减小。而当选取L>300mm后，杨氏弹性模量的相对不确定度将趋于稳定，基本维持在3%左右。实验中心的任课教师在指导学生完成该基础型实验时，就会从测量不确定分析这个角度来讲解杨氏模量测量仪的设计原理，并从测量不确定的角度给出诸如上述学生提出的关于钢丝原长问题的答案，即：通常情况下，杨氏模量测量仪中，钢丝的原长都会设定在大于300mm的范围内。

通过近几年专门针对诸如上述实际实验项目的测量不确定度分析讲解，能够使大多数本科生，特别是物理专业的本科生在完成大学物理实验的同时，不仅能够对实验中心目前开设的实验内容进行全面的学习，而且还能够去深入思考该项实验为什么要采用当前的实验仪器来进行测量，并能够提出针对实验内容的改进方案。这对培养本科生的创新能力起到了很大的帮助。下面，举两个本科生所取得的具体研究成果来说明将测量不确定度分析应用在大学物理实验设计中的重要作用。

迈克耳孙干涉仪实验是目前大部分高校，特别是针对物理专业所开设的基本实验内容之一。利用迈克耳孙干涉仪，实际上可以实现微小伸长量的精确测量。西南交通大学机械学院的两名本科生在经过对测量不确定度分析的深入学习之后，就设计了一种基于迈克耳孙干涉仪的全自动杨氏弹性模量测量仪，用以解决传统实验中采用光杠杆测量所带来的种种缺点。他们通过深入分析基于迈克耳孙干涉仪测量杨氏弹性模量的相对不确定值，设计了一种全自动的杨氏模量测量仪。通过分析发现，他们设计的实验仪可将杨氏弹性模量测量的相对不确定度提高到约0.43%。相比通常用的光杠杆方法，该设计仪器对金属丝杨氏弹性模量的测量精度可提高1到2个数量级。该研究结果以本科生为第一作者，于2016年12月发表于《实验技术与管理》期刊[7]。

利用分光计测量三棱镜折射率也是目前大多数高校所开设的传统实验内容之一。目前，大多数高校开设的此项实验项目为，利用分光计，结合一个等边三棱镜，利用最小偏向角法等测量光源(如汞灯、或者钠灯)某一特征谱线对应的波长，最多再计算一下测量不确定度，给出测量结果的真值在一定范围内的概率，就算很好地完成了本实验内容。西南交通大学应用物理专业的两名本科生，在经过前述的关于不确定度分析在实验仪器设计的应用培训后，就详细地从理论上分析了采用3种(最小偏向角法，掠入射法，垂直底边入射法)常用的分光计测量三棱镜折射率方法时，选取不同顶角的三棱镜，以及针对不同波长的入射光，对所能获得的折射率相对不确定度造成的影响进行了研究，其研究结果可如图2所示[8]。

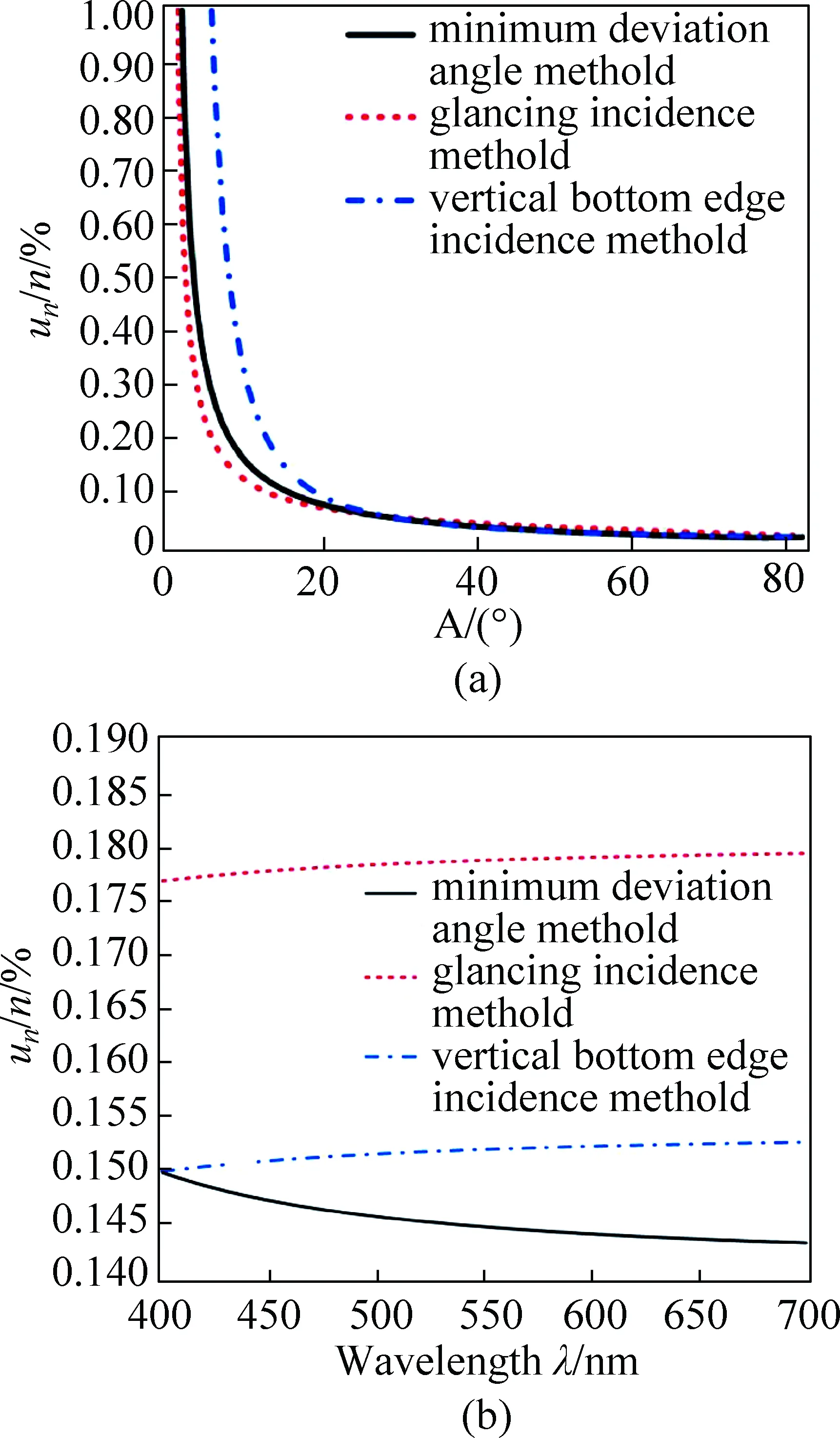
图2 分光计测量三棱镜折射率时，折射率相对不确定度(a) 与三棱镜顶角选取大小的影响； (b) 与被测波长选取大小的影响[8]

从图2(a)中可以看出，当设计的三棱镜顶角较小时，采用掠入射法测量三棱镜的折射率将获得较小的折射率相对不确定度值，且3种方法所得到的折射率相对不确定度都随选取的三棱镜顶角的增大而急剧减小。而当选择三棱镜顶角大于25°后，3种方法所测得的折射率相对不确定度几乎没有差别。从图2(b)中可以看出，随着被测波长值的增加，最小偏向角法可获得的折射率相对不确定度值将减小，而另外两种方法可获得的折射率相对不确定度值将增加。3种方法中，最小偏向角法测量三棱镜折射率可获得较小的相对不确定度值。这样的研究结果，可为利用分光计精确测量三棱镜的折射率的实验仪器设计提供指导作用。该研究成果以本科生为第一作者于2017年12月发表于《激光与光电子学进展》期刊。

从以上的两个实例可以看出，本科生通过对这一基础的分光计测量折射率不确定度的分析，就可以对物理量的精确测量提出改进方案。

3 结语

测量不确定度分析是大学物理实验课程的重要内容之一。通过强化测量不确定度分析在基础性物理实验项目中的应用的讲授工作，西南交通大学物理实验中心进行了一定的大学物理实验教学内容改革。本文通过3个具体的实验项目，详细介绍了我校物理实验中心将测量不确定分析应用于具体实验内容设计中所做的教学改革以及学生取得的研究成果。我们相信，这样的大学物理实验教学内容改革，可为学生设计精确测量物理量的实验仪器提供有力支持，更进一步，为高校培养具有创新实践能力的本科生奠定基础。