白炽灯灯丝的正常发光温度、长度及直径的估算

邵 云

(南京晓庄学院电子工程学院，江苏 南京 211171)

白炽灯是一种热辐射光源，虽然它的电能转换为可见光的效率很低，但因它有良好的显色性和光谱连续性，故仍被广泛地应用于舞台照明、摄影照明、电影放映、生物体内电镜等场合。

白炽灯的设计涉及力、热、光、电4个因素，十分复杂。在钨丝的制作过程中掺入微量的钾、硅、铝元素可以增加它在高温下的力学强度，防止变形。在灯泡中充入稍低于一个大气压的氮气和惰性气体可阻止钨丝的氧化和升华，既可以延长灯丝的寿命，又可以提升灯丝的工作温度以提高光效(温度越高，热辐射中的可见光成分越多)。但是充气又会导致焦耳热通过热传导和对流向外泄露，从而降低了电光转换效率，因此通常只对40W以上的灯泡充气，40W以下则得不偿失。为减少热传导和对流热损耗，人们通常将钨丝做成螺旋状(单螺旋或双螺旋)以减小有效散热面积，这样做的另一个好处便是增加了钨丝的温度，从而提高了光效。

钨丝长度与直径的选择是白炽灯设计的核心问题，它们由灯泡(或灯珠)的功率P、电压U、灯丝的发光温度T三者共同确定，其中必须考虑到螺旋灯丝内彼此间的吸收和反射因素，以及灯泡内气体向外散热因素的影响！

1 白炽灯钨丝长度与直径的理论公式

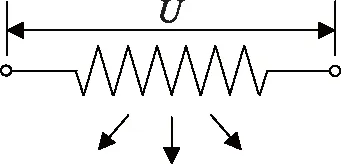
图1 正常发光的钨丝示意图

参见图1，由于钨丝是掺杂的多晶体，因此即使在高温下发光时，它也只能被近似地看作热学中的灰体而非黑体！其通过表面向外热辐射的平均发射率可表示为

εT=-2.9976×10-8T2+2.3435×10-4T-0.1176

(1)

其中T是钨丝(非纯钨)的绝对温度。该表达式是从文献[1]中表格2.2.2的数据经计算拟合得到，适用范围为2000K～3200K。而在正常发光时，长为l直径为d的钨丝向外热辐射的功率可表示成

Pr=δ·εTσT4·πdl

(2)

其中，σT4即为黑体的辐出度；δ则是因螺旋灯丝内部彼此间吸收和反射所带来的折扣因子，称遮挡系数[1]；δ与灯丝的结构有关，对于单螺旋灯丝有δ≈0.755，而对于双螺旋灯丝则有δ≈0.65。

通常灯泡引线和挂钩的热传导损耗很小，几乎可以被忽略。但灯泡内气体的热传导和对流散热却比较可观。气体散热占灯泡电功的比例称为气体热损耗系数，用Kg表示[1]，它与灯泡的功率、泡内气体的类型、灯丝的绕制结构(单螺旋或双螺旋)有关。设灯泡的电功率为

P=UI

(3)

其中，U为灯丝两端的电压；I为电流，则灯泡内气体的散热功率可表示为

Pc=KgP

(4)

在1000K以上较大的温度区间内，钨丝的电阻率可准确地表示成[1]

(5)

长度为l，直径为d的钨丝在其发光时的电阻为

(6)

则根据焦耳定律并结合式(6)得

变形得

(7)

这便是长度为l和直径为d的灯丝所需满足的第一个方程。

将能量守恒定律应用于灯丝有

P=Pr+Pc

(8)

将式(2)、式(4)代入式(8)得

P=δ·εTσT4·πdl+KgP

整理得

(9)

这便是长度为l和直径为d的灯丝所需满足的第二个方程。

联立式(7)、式(9)便可解得

(10)

(11)

再将式(1)、式(5)代入式(10)、式(11)得

这便是长度为l和直径为d的白炽灯灯丝理论公式，它们是由灯丝的焦耳定律和能量守恒定律所推得。从这两公式可见l和d不仅依赖于功率P和电压U，还依赖于温度T及热辐射定律；l和d都是P、U、T的三元函数，其数值是由诸物理定律严格确定的，而不是随意选择的。

2 40W、60W、100W普通充氮泡单螺旋灯丝的正常发光温度T、长度l和直径d

从式(12)、式(13)可见，要想算出l和d，就必须知道灯丝的温度T，而灯丝温度T又与灯泡的光效ηl有如下关系：

(14)

该关系式是根据文献[1]中表格2.2.2的数据并结合该文献中公式(2.4.11)经拟合计算得到。到此，只要知道灯泡的光效ηl，即可从上式推得灯丝的发光温度T。

我国的《JJG 247—2008总光通量标准白炽灯检定规程》[2]规定了常用的普通单螺旋灯丝白炽灯泡光效的基本要求，例如：40W，ηl=8.75lm/W；60W，ηl=10.5lm/W；100W，ηl=12.5lm/W。对于国内最普通的充氮气单螺旋灯丝灯泡，查得它们的气体热损耗系数Kg的平均值分别约为0.30、0.285、0.26，分别将ηl和Kg代入式(14)便可推得这些充氮灯泡灯丝的正常发光温度为

下面利用式(12)、式(13)分别计算这3种灯泡灯丝的l和d。

1) 40W充氮泡单螺旋灯丝的长度与直径

将T=2590K、P=40W、U=220V、Kg≈0.30、δ≈0.755、斯特藩-玻耳兹曼常量σ=5.67×10-8W·m-2·K-4一起代入式(12)和式(13)即可求得l=0.685m，d=2.34×10-5m。

2) 60W充氮泡单螺旋灯丝的长度与直径

将T=2680K、P=60W、U=220V、Kg≈0.285、δ≈0.755及σ一起代入式(12)和式(13)可求得l=0.705m，d=2.97×10-5m。

3) 100W充氮泡单螺旋灯丝的长度与直径

将T=2760K、P=100W、U=220V、Kg≈0.26、δ≈0.755及σ一起代入式(12)和式(13)可求得l=0.772m，d=4.08×10-5m。

可见，普通充氮泡单螺旋灯丝的正常发光温度T、长度l、直径d均随功率P的增加而增加。

式(14)右边括号内的三次方程实际上是文献[1]表格2.2.2中钨丝发光效率η数据的近似拟合，在2000K～3200K的温度区间内，η与T几乎呈线性正相关；同时，从上文可见Kg应与T反相关，因此灯泡的光效ηl(注：不同于η)一定与T正相关，也就是说提高灯丝的温度便能提高灯泡的光效。那么为什么不将40W和60W的灯丝温度也提高到2760K来提高光效呢？这是因为单纯提高温度会导致灯丝的直径减小，这已由式(12)验证。于是单位长度灯丝的侧面积、体积也随之减小，但体积减小比例更大。与同温的100W灯丝相比，40W和60W灯丝表面的钨原子相对于钨丝质量的升华速率无疑要快得多，它们的寿命将大大缩短，因此这种美好的设想是不现实的。低功率灯丝选择低的工作温度正是出于对其使用寿命的考虑。

不过，从式(12)、式(14)可见，要想功率P不变，工作温度T升高以提高光效，同时灯丝直径d增加以保证使用寿命，那么只能要求灯泡内气体的热损耗系数Kg减小或灯丝的遮挡系数δ减小，或者两者同时减小。充氩气的双螺旋灯丝灯泡能满足此要求，它的Kg比充氮泡的单螺旋灯丝小得多，且δ也比单螺旋灯丝小，因此它的灯丝工作温度可以更高，光效也更高。遗憾的是，由于双螺旋灯丝的制作难度大、成本高，不易推广，因此大多数企业宁愿生产充氩气的单螺旋灯丝灯泡[3]。

3 基于基本光效的充氩气灯泡单螺旋灯丝的正常发光温度T、长度l和直径d

对于充氩气(氩气占85%，氮气占14%)的单螺旋灯丝灯泡，查得它们的气体热损耗系数Kg的平均值分别约为0.20(40W)、0.185(60W)、0.17(100W)，结合它们的基本光效ηl值：8.75lm/W(40W)、10.5lm/W(60W)、12.5lm/W(100W)，代入式(14)可解得这些基本光效充氩气灯泡灯丝的正常发光温度为

1) 基本光效下40W充氩泡单螺旋灯丝的长度与直径

将T=2520K、P=40W、U=220V、Kg≈0.20、δ≈0.755及σ一起代入式(12)和式(13)即可求得l=0.826m，d=2.53×10-5m。

2) 基本光效下60W充氩泡单螺旋灯丝的长度与直径

将T=2605K、P=60W、U=220V、Kg≈0.185、δ≈0.755及σ一起代入式(12)和式(13)即可求得l=0.851m，d=3.21×10-5m。

3) 基本光效下100 W充氩泡单螺旋灯丝的长度与直径

将T=2690K、P=100W、U=220V、Kg≈0.17、δ≈0.755及σ一起代入式(12)和式(13)即可求得l=0.912m，d=4.37×10-5m。

将这里充氩泡的结果与前面第2节充氮泡的结果对比发现，在功率和光效均相同的情况下，充氩泡的灯丝温度普遍下降了70K，灯丝长度普遍增加了20%，直径普遍增加了8%。可见充氩泡灯丝的使用寿命将大大地延长，但是光效不变，用料成本却大大地增加，这或许是一种浪费，即我们可以牺牲掉灯丝的一部分使用寿命来换取更大的光效和更低的成本。

4 一种实用的充氩气灯泡单螺旋灯丝的设计方案及对比分析

文献[1]给出了国内不少厂家设计单螺旋灯丝充氩气灯泡l和d的一种制造经验公式(误差在2%左右)：

其中电流的单位是A。这样便可直接通过式(15)、式(16)计算出l和d，再将它们与Kg、δ一起代入式(12)、式(13)估算出灯丝的工作温度T，然后再代入式(14)算出灯泡的光效ηl。

1) 40W充氩气单螺旋灯丝实用灯泡

将40W灯泡的电流I=40/220≈0.182(A)代入式(15)、式(16)求得灯丝的长度与直径：l=0.709m，d=2.43×10-5m。将它们代回到式(12)、式(13)推得灯丝的发光温度大致在2620K，继而从式(14)算得灯泡的光效ηl=10.6lm/W。

对比前文基本光效下40W充氩泡的结果：

可见，这里按经验公式制造的实用灯泡光效更高、成本更低；当然，由于灯丝的温度增加了100K而直径减小了4%，因此它的使用寿命会短不少，但仍能符合规定要求(见下文)。

若将充氩气的实用灯泡与前文基本光效下的40W充氮气泡结果：

相比较可见，充氩实用灯泡的l、d稍微增加了一点，但光效显著增加。至于使用寿命，虽然灯丝温度增加了30K即1.2%，但灯丝半径也增加了2.6%，加之氩气分子的质量显著大于氮气分子，使得氩气比氮气更能阻止钨丝的升华，这些因素最终能使40W充氩实用泡的使用寿命大于前文40W的充氮泡，即能符合灯丝使用寿命要求。

2) 60W充氩气单螺旋灯丝实用灯泡

将60W灯泡的电流I=60/220≈0.273(A)代入式(15)、式(16)求得灯丝的长度与直径：l=0.797m，d=3.15×10-5m．将它们代回到式(12)、式(13)推得灯丝的发光温度大致在2645K，继而从式(14)可算得灯泡的光效ηl=11.3lm/W。

对比前文基本光效下60W充氩泡的结果：

可见，按经验公式制造的实用灯泡光效更高、成本更低；当然，由于灯丝的温度增加了40K而直径减小了2%，因此它的使用寿命会短一些，但仍能符合规定要求(见下文)。

再对比前文基本光效下60W充氮泡的结果：

可见，充氩气实用灯泡的l、d、ηl均增加了一些，但T却减小了一些，加之本身充的是氩气，因此它的使用寿命一定比基本光效下60W的充氮泡长。

3) 100W充氩气单螺旋灯丝实用灯泡

类似可求得灯丝的长度l=0.922m，直径d=4.38×10-5m，正常发光温度T≈2680K，光效ηl=12.3lm/W。

对比前文基本光效下100W充氩泡的结果：

可见，两者基本一致，也就是说100W的实用充氩泡就是按照基本光效要求设计的。

再对比前文基本光效下100W充氮泡的结果：

可见，充氩气实用灯泡灯丝的温度低了80K，长度、直径却增加了不少，而光效基本持平。这不能被算作是一种浪费，而是实践中出于保证灯泡使用寿命的考虑，这就意味着前文基本光效下100W充氮泡的使用寿命可能达不到1000h的标准要求。由此可见，大功率的灯泡要想保证其使用寿命及光效，就必须充氩气等大分子的惰性气体。从式(14)可见，在光效ηl一定而降低了热损耗系数Kg后，灯丝的工作温度T便降了下来(相对于大功率充氮泡)；又从式(12)可见灯丝的直径增加了，于是灯泡的使用寿命便延长了。

5 总结与说明

本文利用所推得的理论公式(12)、式(13)、式(14)分别完整地计算了JJG 247—2008规定的基本光效下常见的40W、60W、100W普通充氮、充氩白炽灯单螺旋灯丝的正常发光温度T、长度l和直径d，同时从一种实用的经验公式(15)、式(16)结合式(12)、式(13)算得同样功率的实用充氩白炽灯丝的对应参量。将这3种灯泡灯丝的结果进行对比分析发现，基本光效下的普通充氮泡灯丝的温度偏高，直径偏小，寿命偏短，其中100W灯泡的使用寿命可能达不到标准要求；基本光效下充氩泡灯丝的温度偏低，直径偏大，寿命偏长，有用料成本偏高而光效偏低之嫌；经验公式制造的实用充氩泡灯丝的温度随功率变化不大，数值处在不高不低的位置，直径总体居中，寿命也适中，但光效大，确实实用。

本文所给理论公式(12)、式(13)、式(14)较文献[1]中公式更完整、深入、便于计算。它们揭示了灯丝的长度、直径、温度与灯泡的功率、结构、充气性质、光效及使用寿命等因素的内在关联。3种灯泡的数据结果对比合乎物理逻辑，显示出理论公式(12)、式(13)、式(14)的正确性。

从文中诸结果可见，白炽灯丝的正常发光温度T、长度l和直径d均与功率正相关。那种认为功率越大则灯丝的长度越短、直径越粗的观点是肤浅的，同样，那种认为可以通过单纯提高灯丝温度来提高低功率灯泡光效的观点也是错误的。

公式(12)、式(13)、式(14)中的遮挡系数δ和气体热损耗系数Kg本文均选择了均值，即参考的是灯丝几何参数的均值，具有代表意义。其中Kg的取值来自文献[1]中的曲线图2.4.2，可能存在少量误差，但文献[4]中的插图5又显示本文Kg取值的误差其实很小。另外，从本文的理论结果和经验公式结果均合乎物理逻辑来看，Kg及理论计算的误差应不大。

如果能够直接测得灯丝准确的正常发光温度T，便可直接从公式(12)、式(13)、式(14)计算出灯丝的长度l、直径d和灯泡的光效ηl；反之，如果l、d已知，那么也可以反过来推定灯丝的温度T及灯泡的光效ηl。

由于更低功率的灯泡要么是真空泡，要么Kg变得很大，从文献[1]的曲线图2.4.2中不易估读，而更高功率灯泡的导线传热比例也渐增大，不容忽视[5]，因此本文只计算了40W、60W和100W的充气灯泡。

6 结语

本文主要参考的文献[1]是复旦大学教材《光源原理与设计》。本文所给完整的理论计算公式(12)、式(13)、式(14)，及其与经验公式(15)、式(16)在具体实例中的详细应用以及对比分析，或可为相关内容的教学提供点滴参考。不当之处，欢迎指正。