向量在立体几何当中的应用

元凌燕

【摘要】“向量”最早出現在欧洲19世纪20年代，由两个数学家提出.起初它是用于表示复数的形式，在时代的发展中人们提出了维度的概念，人们将向量与维度概念相结合，进而提出了三维、四维乃至n维的概念.其中向量在物理学中也有很大的应用，物理学中的矢量指的便是向量，用来代表有大小有方向的量.向量在学生的学习中占有很大的比重，在社会生活中其具有很大的利用价值.本文主要介绍高中学习中关于向量的概念以及在立体几何方面的应用.

【关键词】向量;重要性;学习向量

传统的计算分析方法在计算空间类问题时存在着很多无法有效解决的问题，向量的出现为解决空间类问题提供了新的思路，以向量为基础，使用代数运算进行空间类问题解析成为当下解决立体几何问题的主要方式.在高中阶段，充分理解向量概念，熟练运用向量关系可以为大学代数学习提供一定的基础，同时也为当下解决立体几何问题提供一定的新思路.

一、向量学习的重要性

（一）向量使用广泛

1.生活中的向量概念使用

随着科技的不断发展，知识改变生活的概念越加凸显，在生活中处处都可以看到向量的使用，向量使人们的生活质量有了很大的提升.如，在进行铁道、桥梁建设时，要想建设两边同时开工而又不出现偏差时就需要使用向量，保证在最后的连接过程中不会出现问题.

2.软件中处处有向量

在这个信息时代，人们使用着各型各色的软件，在软件的研发与设计过程中无处不体现着向量的使用.如，微信、qq中精美的图片在任何手机上放出都不会出现模糊，这就是由于照片是使用向量进行设计的，换言之照片在传输过程中是通过传输向量式而非传输像素点位置.在建设工程中cad、sordwork等建筑软件在进行绘图时也全都使用着向量的原理，通过向量可以绘制出完美的直线.

现在人们的生活中处处都有着向量的使用，向量已经在潜移默化中改变着人们的生活.学习向量的概念与运用方式对人们有着极大的好处.高中生作为祖国的未来，承担着祖国未来发展的重责，学习向量则是他们获得知识提高，为祖国发展奉献的最佳途径.

（二）向量在解决问题方面有独特优势

向量在解决空间类问题有很大的优势，本文主要介绍其中的一类，使用向量求直线与平面之间所成的角.

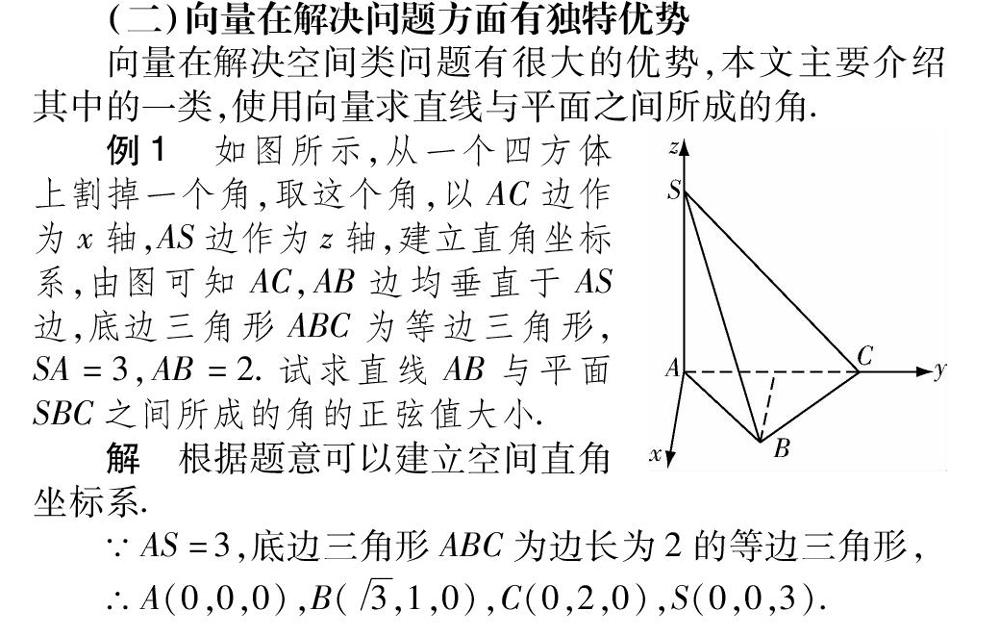
例1 如图所示，从一个四方体上割掉一个角，取这个角，以AC边作为x轴，AS边作为z轴，建立直角坐标系，由图可知AC，AB边均垂直于AS边，底边三角形ABC为等边三角形，SA=3，AB=2.试求直线AB与平面SBC之间所成的角的正弦值大小.

解 根据题意可以建立空间直角坐标系.

∵AS=3，底边三角形ABC为边长为2的等边三角形，

∴A（0，0，0），B（3，1，0），C（0，2，0），S（0，0，3）.

设平面的法向量等于（x，y，z），法向量垂直于向量 SB与向量SC，则可列方程组，再设x等于1，求得法向量n的为1，3，232.

∵直线AB与平面SBC所成的夹角的正弦值等于法向量与直线AB之间所成的角的余弦值.[1]

∴有向量式：AB·n=|AB|·|n|·cosα.

又∵AB·n=（3，1，0）·（1，3，233），法向量n=433，

∴cosα=34，即直线与平面SBC之间的角正弦值为34.

二、如何帮助学生理解学习向量

（一）明确教育方式

先学后教，让学生成为课堂的主人是解决学生学习难，学习不用心的最佳方式，是当下教育改革中所倡导的改革方式，在进行向量学习中同样也应该应用这样的教育举措.在上课之前给学生留下有关向量的问题，启发学生积极进行思考，在课上通过提问题的方式进行传授，学生在回答问题中获得成长[2].高中生都有着积极求知的兴趣，只要有一定的引导便可以自主进行学习，教师通过提问的方式促进学生思考.

（二）实战的主要步骤

根据上面理论运用在空间向量学习教学中的过程如下：

1.课前

在上课前一天教师通过提出问题“平面上从A点到B点之间，怎么画线最短”的问题引出空间中两点如何画线最短？留给学生思考，同时让学生预习书上的内容以及尝试用坐标系描述一个图形各个顶点的坐标.学生在好奇心的驱使下便会开始学习研究立体坐标系，进而对学生形成立体坐标系意识打下基础，防止学生在授课过程中难以理解立体坐标系.

2.课上

在课上，首先是进行成果展示环节，让学生各自展示自己如何在一个立体图形上画最短的线，之后询问如何计算线的长短，进而证明空间中勾股定理同样适用.同理还可以由平面上两条线之间的距离是作一条同时垂直于两条直线的线引出空间中距离的计算公式.对一些较难的问题可以通过教师留下问题，下次上课学生在展示，教师在评价讲授的方式，增加学生的印象，进而保证上课的质量.

三、结束语

向量是工科、理科学习的基础，是保障我国经济发展的基础.高中生作为祖国建设的新一代，帮助高中生熟练掌握向量这一工具是促进我国经济发展的最佳途径.当前应该帮助学生掌握向量在空间中的用法，促进学生形成立体意识，进而为国家输送大量高质量人才.

【参考文献】

[1]王建明.《高中课标》和《高中大纲》之空间向量与立体几何的比较[J].北京教育学院学报，2005（2）：165-169.

[2]黄梅花.浅析立体几何之空间向量应用难点[J].数理化学习（高一二版），2016（9）：135-136.