苏教版《普通高中课程标准实验教科书(必修)数学》中核心概念认知情况的调查报告
2019-07-08程仕然蒋智东
程仕然 蒋智东

[摘 要] 文章通过对省内部分师生的问卷调查和访谈调研,了解苏教版高中数学核心概念在广大师生心中的认知情况,通过数据处理和相关对比分析,坚定了苏教版核心概念研究的必要性和重要性,也为相关研究指明了方向.
[关键词] 高中数学;核心概念;认知;调查;苏教版
研究的背景
1. 研究的起因
我们知道,数学概念是数学课程知识体系的基本单位,而核心概念作为数学概念体系的中心和主干,更是数学教学和数学学习领域研究的关键内容. 数学核心素养对教师的课堂教学和学生的学习都提出了新的要求和挑战,对核心概念的研究有助于我们对知识板块的整体把握,可以起到牵一发而动全身的作用,也为其他概念的学习起到示范作用. 抓住数学核心概念的教与学,就抓住了数学教与学的精髓,纲举目张,从而达到本学科教与学的良好发展.
然而,尽管高中数学核心概念的相关研究有很多,成果也很丰富,但是高中数学核心概念到底有哪些?核心概念和重要概念有什么区别?核心概念和考试常考的主要概念有什么区别?如何更好地进行核心概念的教学,如何把核心概念的引领带动作用体现出来等等问题,一直众说不一,困扰着广大教师. 但正因为这样,也一直激励着更多的教师在这方面进行研究和探索.
通过前期的理论学习和研究,借鉴人教版核心概念研究,我们认为苏教版《普通高中课程标准实验教科书(必修)数学》中的“函数”“向量”为“代数”模块的核心概念,“斜率”“正(余)弦函数”“异面直线”为“几何”模块的核心概念,“随机事件”“概率”为“概率与统计”模块的核心概念. 但是这些认定是否科学,能否得到大家的认可,我们还是没底的.所以,希望通过本次调查研究,调查一下普通学生及一线数学教师心目中的高中数学核心概念,以及对核心概念的理解和认识,从而研判我们当初所预测的几个核心概念是否成立,进而确定我们课题组的具体研究对象.
2. 高中数学核心概念及其界定
数学核心概念的研究早就引起数学教育界的关注,相关成果丰富多样,其中以美国的相关研究更深入,更具有指导实践的意义. 美国国家数学教师理事会(NCTM)2000年发布的《学校数学教育的原则和标准》中明确提出了“数与运算”“代数”“几何”“度量”和“数据分析与概率”五个领域的内容标准,旨在设立面向所有学生的课程核心. 在高中数学核心概念研究方面,从代数领域、几何领域和数据分析与概率领域三个方面分别给出核心概念图. 但这些研究尚未和国内研究接轨,大多数高中数学教师了解甚少,更不要说学生了.
在国内的相关研究中,章建跃博士系统地进行了“中学数学核心概念思想方法结构体系及其教学设计的理论与实践”研究,认为:“中学数学核心概念”是指那些处于“核心地位”的概念,是中学数学课程中的主要概念,是中学数学知识结构中的“联结点”,由其反应的数学思想方法是联系数学知识的纽带.
其他关于中学数学核心概念的研究大致可概括为:核心概念是在确定范围的数学知识体系中,处于中心位置的概念性知识,具有根基性、可生长性、广泛联系性,是学科结构的主干,主要有原始概念、思想贯穿、变革标志三种形式,在知识体系中起着核心、不可替代的作用.
3. 调查研究的意义
(1)明确高中数学教材中的核心概念及其核心概念体系,提高教师自身的数学修养
中学数学核心概念往往具有鲜明的直观背景,简单、易懂且威力无穷,是开启中学数学大门的金钥匙. 广大教师应加强修行,远离“题型+技巧”的雕虫小技,集中注意力于核心概念,这样才能实现“减轻负担,提高质量”的宏愿.
明确高中数学教材中的核心概念及其核心概念体系,有助于教师形成对知识比较系统的感知,做到深层次的领会.在这个过程中增加自己的学科知识,增强自身认知的数学中普遍联系性,提高自己的数学修养.
(2)培养学生的数学素养,帮助学生形成数学整体知识结构
我们知道,数学概念是人类对现实世界空间形式和数量关系的概括反映,是建立数学法则、公式、定理的基础,也是运算、推理、判断和证明的基石,更是数学思维、交流的工具.
学生数学的学习过程必定要经历感受、观看、比较、本质化、数学符号表征、证明等一系列过程,思维力的培养需要进行数学概念学习时着手开始,在这些步骤中训练着思维的力量,帮助完成数学素养的提高.
(3)指导教师实际教学,实现课堂上对数学知识本质的冷静思考
课堂教学中,围绕核心概念来组织知识,是一种非常经济和有效的组织科学课程或教学活动的方式;课程内容围绕核心概念组织展开,课堂教学帮助学生掌握核心概念,将有助于学生对知识的深入理解和迁移应用.
研究过程
1. 研究方法
本次调查研究采用问卷调查及与部分教师访谈调研的形式进行.通过前期的文献研究,分教师版和学生版编制了《苏教版〈普通高中课程标准实验教科书(必修)数学〉中核心概念的调查问卷》,借助网络问卷星平台进行在线匿名的答卷方式. 学生版问卷共10个问题,2个填空,5个单选,3个多选;教师版共7个问题,2个填空,2个单选,3个多选;对师生的教龄(年级)分布,对高中核心概念的了解情况,对高中三大模块中核心概念的认知情况等.
2. 研究的對象
调查分别对苏州市相城区内两所四星高中、一所三星高中的部分在校高二学生和江苏省范围内部分高中数学教师及部分数学教育专业在校师范生进行了调查. 有效答卷回收教师问卷202人,学生问卷358人. 利用教研活动、本校对外交流活动、蒋智东名师工作室活动,外出学习等机会访谈调研高中数学教师67人次.
3. 研究的信度和效度
问卷调查结束后,对调查数据进行分析.信度方面:教师版和学生版调查的Cronbach α系数为0.862,大于0.8,说明各项得分的一致性较好,研究数据信度质量高. 针对“项已删除的α系数”,分析项被删除后的信度系数值并没有明显的提升,因而说明题项全部均应该保留,进一步说明研究数据信度水平高,可用于进一步分析.效度方面:对教师版和学生版调查核心概念数据设置10个因子进行效度分析,KMO值均为0.851,高于0.8,说明效度高,研究项合理且有意义.调查问卷反馈的数据清晰,指向明确,能够解决预期问题.
调查的内容
本次调查研究的核心概念范围是苏教版高中数学必修教材中“代数”“几何”“概率和统计”三个模块.按照上面我们提供的核心概念的界定或结合调查对象自己的认识在下面的三个模块中,分别选出10个自己认为是该模块的核心概念.
苏教版数学高中必修教材中代数模块中共有85个概念:元素、集合、“属于”、“不属于”、集合的列举法、集合的描述法、子集、Venn图、集合相等、真子集、空集、并集、交集、全集、补集;函数、定义域、值域、开区间、闭区间、半開半闭区间、分段函数、映射、增函数、减函数、最大值、偶函数、奇函数;N次方根、根式、根指数、被开方数、指数函数、对数、底数、真数、常用对数、自然对数、对数函数、反函数、幂函数;函数的零点、二分法;算法、程序结构、程序语句、辗转相除法(欧几里得算法)、秦九韶算法、基数、除2取余法;向量、向量的长度(模)、零向量、单位向量、平行向量(共线向量)、相等向量、向量的加法(三角形法则、平行四边形法则)、向量的数乘、基底、向量的夹角(向量垂直)、向量正交分解、向量的坐标表示、向量的数量积、向量在方向上的投影;数列、数列的项、首项、有穷数列、无穷数列、通项公式、等差数列、公差、等差中项、数列的前n项和、等比数列、公比、等比中项;一元二次不等式、二元一次不等式、二元一次不等式(组)的解集、线性规划、可行解、可行域、目标函数、线性目标函数.
苏教版数学高中必修教材中几何模块79个概念:棱柱、棱锥、圆柱、圆锥、棱台、圆台、柱体、椎体、台体、球体、斜二测画法;直线在平面内、异面直线、异面直线所成的角、(空间内)两直线垂直、直线与平面平行、平面与平面平行、直线与平面垂直(平面的垂线、直线的垂面、垂足)、二面角(二面角的棱、二面角的面、二面角的平面角)、平面与平面垂直;直线的倾斜角、直线的斜率、直线的方程(点斜式、斜截式(截距式)、两点式、一般式);圆的标准方程、圆的一般方程;空间直角坐标系(坐标原点、坐标轴、坐标平面)、右手直角坐标系、空间直角坐标系中的坐标(横坐标、纵坐标、竖坐标);正角、负角、零角、任意角、象限角、角度制、弧度制、弧度、单位圆、正弦、余弦、正切、有向线段、正弦线、余弦线、正切线、三角函数线、正弦函数、余弦函数、正弦曲线、余弦曲线、周期函数、周期、最小正周期、“简谐运动的振幅、频率、相位、初相”;和角公式、差角公式、倍角公式;正弦定理、解三角形、余弦定理.
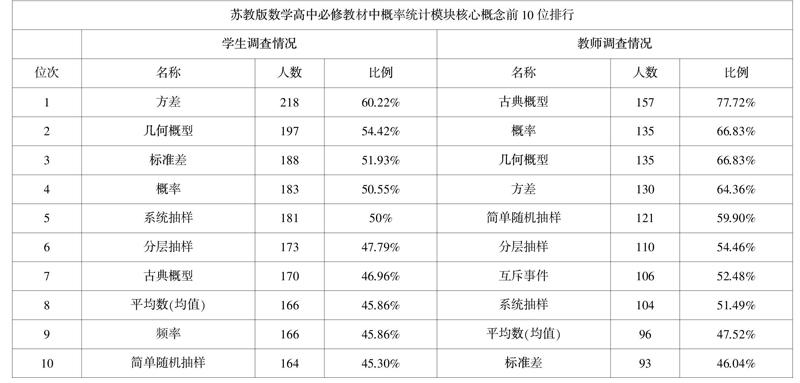
苏教版数学高中必修教材中概率统计模块29个概念:概率与统计、简单随机抽样、系统抽样、分层抽样、频率分布、频率分布表、频率分布直方图、频率分布折线图、茎叶图、平均数(均值)、标准差、方差;散点图、线性相关关系、线性回归方程、最小二乘法;确定性现象、随机现象、必然事件、不可能事件、概率、频数、频率、互斥事件、对立事件、概率的加法公式、基本事件、古典概型、几何概型.
