培养问题意识渗透思想方法

郭松 于静

教学内容：人教版数学三年级上册第八单元90～91页。

教学目标：

1.使学生初步认识几分之一，认识分数各部分名称，会读写几分之一，能比较分子是“1”的分数的大小。

2.让学生经历从日常生活中抽象出分数的过程，通过操作、观察、比较、概括等活动培养学生的观察能力和动手操作能力，使学生的思维得到发展。

3.经历认识分数的过程，体验创造的快乐，感知数学来源于生活并运用于生活，对数学产生亲切感，获得成功体验。

教学重、难点：初步理解分数的含义，正确读写几分之一，会比较分子是“1”的分数的大小。初步建构分数概念，理解分数表示的实际含义。

课前交流：

师：在老师的描述中，猜一猜这个人物是谁？他生在东海之滨，无父无母，饱受日月精华，海水拍打，在一块石头中诞生……

生：孙悟空。

师：后来他到了花果山，再后来——

生：他做了美猴王，最后他保护唐僧去西天取经。

师：哦，这就是《西游记》。和他一起去取经的还有谁？

生：猪八戒，沙僧，还有一匹白龙马。

师：下面我们就从在《西游记》中的一个有趣的故事开始这节数学课好吗？

生：好！

教学过程：

一、情境导入，问题引发冲突

（PPT播放《偷吃人参果》。）

师：请同学们读一读孙悟空的问题：“如果摘了9个人参果，兄弟3人该怎么分？”同学们，你们能帮他分一分吗？

生：9÷3=3（个）。

师：这种分法在数学中就叫做——

生：平均分。

师：我们看看八戒是怎样想的。八戒说：“我最胖，我吃7个，你们2人每人一个！”请问这样分公平吗？

生：不公平。

师：那怎样分才公平呢？

生：平均分。

师：孙悟空又说：“如果摘了6个人参果，兄弟3人该怎么分？”

生：6÷3=2（个）。

师：这种分发是——

生：平均分。

师：孙悟空再次说道：“我只摘回来4个，咱们3人该怎样分呢？”同学们有什么办法吗？

生：可以把人参果切开分。

师：首先每人能分到几个？

生：1个。

师：每人分到1个，还剩几个？

生：还剩下1个。

师：孙悟空是大师兄，非常谦让说：“剩下一个我不吃了，你们2人分了它吧。”八戒和沙僧2人该怎么分呢？

生：每人一半。

师：我看看八戒是怎么说的，他说：“我们每人一半，公平吗？”

生：公平。

师：八戒说切了它，每人一半。看看这样切行不行？

（课件演示。）

生：不行。

师：为什么不行？

生：因为人参果上面小，下面大。

师：不是一样大，也就是不是——

生：不是平均分。

师：要想分得公平，就必须要平均分。那该怎样切才是平均分呢？

生：竖着切。

师：竖着切就是平均分了吗？

生：不是，要切的两面都一样大。

（课件演示。）

師：终于分好了，他们2人可以吃人参果了，悟空又跑出来问道：“一半应该用哪个数字表示呢？”

生：可以用0.5表示。

师：可以用小数表示，还可以用什么数表示？

生：可以用表示。

师：你是在哪里见到过这样的数字？

生：生活中。

生：书上。

师：同学们，在生活中我们也经常遇到这样的难题，人们用这样的数字表示。今天我们就一起来研究一下这样的数是怎样产生的。

（课件演示分数的产生，引出新课。板书课题：分数的初步认识。）

【评析】用动画和问题情境引入新课，前两个问题激活学生原有的认知结构，第三个问题引发认知冲突，强调“平均分”是为后面分数的产生奠定基础，过渡到新知识的学习，激发学生的学习兴趣。

二、动手实践，直观排除冲突

（一）情境探索，教学例1

1.课件演示，感受二分之一的由来。

师：沙僧告诉我们：把一个人参果平均分成2份，每份就是这个人参果的一半，也就是它的二分之一，写作：。

师：像这样的数就是分数。同学们，你们对它有什么了解和认识吗？沙僧说的这句话你理解吗？和你的同桌讨论交流一下你对这句话的理解和对这个数的认识。

（学生讨论交流。）

师：经过讨论，你们对这句话和这个新认识的分数有哪些疑问？

生：下面的2表示什么呢？

生：为什么中间有个横线呢？

…………

师：我们现在来解决这些疑问。把一个人参果平均分成2份，每份就是这个人参果的一半，也就是它的二分之一，写作：。其中有两个关键词，第一个是“平均分”，另一个是“它”。在分数中这个横线叫做分数线，它表示平均分。将人参果平均分成了2份，分数中的2就是平均分的份数。分数中的1表示平均分成2份中的1份。同学们，你们觉得这个分数该怎样书写呢？（生回答。）

师：应该先写分数线。因为这样写更容易帮助我们理解分数的含义，也可以写得更加整齐。

（教学写法及分数各部分的名称。）

2.知识点平行延伸。

师：一半人参果可以这样用分数表示，其他的物体被平均分成2份，其中的一份也可以这样表示吗？

生：可以。

（课件出示：孙悟空分月饼。）

师：谁能完整的表达？

生：把一块月饼平均分成2份，每份是它的二分之一。

3.实践分物，体会二分之一的意义。

师：同学们，知道这个数字是怎样产生的了吗？

生：知道了。

师：那你们想不想自己创造一个呢？

生：想。

师：同学们手中有各种形状的学具卡，你们能不能自己动手折一折，把学具卡平均分成2份，感受一下的由来，然后按照“把（   ）平均分成2份，每份是它的（    ）”的句式表达出来。

（教师板贴词条：“把（   ）平均分成2份，每份是它的（    ）分之一”，引导学生用严谨的数学语言表达。学生动手实践后展示。）

生：把一个圆平均分成2份，每份是它的二分之一。

师：左边一半是这个圆的，右边一半也是这个圆的，这两个合在一起是多少呢？和你的同桌讨论一下。

生：两个合起来是1，因为两个一半的圆合起来就是一个圆，就能用整数1表示了。

师：同学们，你们明白了吗？

生：明白了。

师：刚才这位同学用的是圆，哪位同学用的是正方形？展示一下。

生：把一个正方形平均分成2份，每份是它的二分之一。

师：这两种分法都可以吗？为什么？

生：可以。两种方法都是平均分。

师：一个图形不管用怎样的方法，只要是平均分成2份，每份就是它的二分之一。

师：用长方形的同学也展示一下吧。

（课件演示。）

师：同学们可以通过对折得到第一种分法吗？

生：不能。

师：那这种分法是不是平均分呢？

生：是的。

【评析】通过教师演示、学生操作，从实物延伸到图形，从直观延伸到抽象，层层递进，初步理解分数的产生及分数的意义。

（二）整合文本，教学例2

1.拓展分物，初步理解分数的意义。

师：我们刚刚用对折的方法平均分物创造了二分之一，你们还想不想创造出其他的分数呢？

生：想。

师：那你们觉得再创造出几分之一比较容易？

生：四分之一。

师：为什么四分之一比较容易？

生：因为把我们刚刚创造出的二分之一再对折一次，就创造了四分之一。

师：那同学们就用学具卡创造出一个四分之一好吗？请同学们动手做起来吧。

师：同学们创造出了四分之一，和你的同桌互相用句式说一说。

（点名汇报，应用“教学助手——随堂直播”将学生作品展示到大屏幕上。）

生：把一個正方形平均分成4份，每份是它的四分之一。

生：把一个长方形平均分成4份，每份是它的四分之一。

生：把一个圆平均分成4份，每份是它的四分之一。

师：一个图形只能被平均分成2份或4份吗？还可能被平均分成几份？每份是它的几分之几呢？

生：还能平均分成6份，每份是它的六分之一。

生：还能平均分成8份，每份是它的八分之一。

…………

2.练习。

师：我们已经认识了这么多的分数了，那么现在我们一起来完成一个练习题。

（课件出示。）

判断下列哪个图中涂色的部分可以用表示？可以的画√，不可以的画×。

师：第一幅图可以吗？谁能说一说原因？

生：不可以，因为不是平均分。

师：第二幅图可以吗？

生：可以。

师：第三幅图呢？

生：不可以，因为涂色部分是三分之一。

师：第四幅图呢？

生：可以。

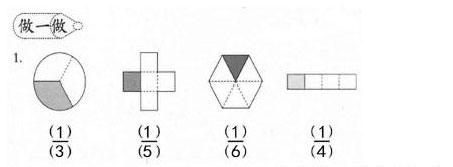
师：接下来请同学们独立完成数学书91页上“做一做”的第1题。

（学生汇报，课件出示。）

师：题目中三分之一、五分之一这样的分数，不容易通过对折的方法创造出来，但是一个图形并不是不能被平均分成3份、5份。

（教师演示：一个圆被平均分成3份，每份是它的三分之一。板书：。一个圆被平均分成5份，每份是它的五分之一。板书：。）

【评析】学生通过动手实践、同桌交流和教师拓展追问，学以致用，再次加深对分数意义的理解。

（三）情境设疑，教学例3

1.直观认知，掌握分数大小比较方法。

师：我们懂得了这么多分数的知识了，忘了偷吃人参果的那几位了，看看他们在干什么呢。

（出示课件：八戒问：大，还是大？）

师：和你的同桌讨论交流一下，看看究竟是谁大呢？

生：二分之一大。

师：为什么？

生：因为二分之一是把一块月饼平均分成2份中的一份，而四分之一是把一块月饼平均分成4份中的一份。分的份数越多，每一份就越小。

师：他说的你们听懂了吗？

生：听懂了。

师：观察一下这两个分数，你还有什么发现吗？

（板书： >。）

生：哪个分母小，哪个分数就大。

生：分子相同。

师：你们发现比较这两个分数大小的规律了吗？

生：分子相同，分母越大，分数越小。

师：黑板上还有一些分数，我们用这个规律比比大小吧！

生：>。

（出示课件。）

2.练习。

师：同学们都学会这样比较分数大小的方法了吗？请马上独立完成91页“做一做”第2题。

（学生汇报，课件演示。）

【评析】通过实践操作、合作探究，判断出分数大小，发现规律，总结提炼出同分子分数比较大小的方法，并能应用所学规律，熟练操作。

三、回顾总结，交流体会收获

师：通过这节课的学习，同学们有哪些收获？

生：我知道了什么是分数。

生：我知道了分子相同，分母越大，分数就越小。

生：我还知道了分数的写法：分母写在分数线的下面，分子写在上面。

…………

师：这节课大家一定都有很多的收获，所以我给同学们准备了一些习题。请用你今天的收获去完成这些习题，展示给你的家长看看，好不好？

师：最后老师送给同学们一句话：成功等于百分之一的天赋加百分之九十九的努力。我祝愿同学们通过自己的天赋和努力去创造幸福完美的人生。

【评析】通过回顾和总结，让学生再次将全课所学浮于脑海。让学生用自己的语言表述，了解学生在学习活动中获得了什么样的情感体验，为今后的教学查缺补漏。

总评：

本节课是小学数学人教版三年级上册第八单元90～91页的内容，属于数与代数领域，是在学生已掌握一些整数知识的基础上进行教学的。从整数到分数既是数的概念的一次扩展，又是学生认识数的概念的一次质的飞跃。无论在意义上，还是在读写方法上，分数和整数都有很大的差异。本课内容是“初步认识几分之一”，它是认识几分之几的基础，是本单元教学内容的“核心”，也是整个单元的起始课，对以后学习起着至关重要的作用。

1.以课程标准为依据，设计层次，突破重、难点。

《数学课程标准》中指出：“课程内容的组织要重视过程，处理好过程与结果的关系;要重视直观，处理好直观与抽象的关系;要重视直接经验，处理好直接经验与间接经验的关系，课程内容的呈现应注意层次性和多样性。”郭老师牢牢地把握住了这一点。授课过程将情境贯穿始终，从导入新知的探索到全课的总结，让学生融入到教师创设的情境中，全体师生共同在情境中发现问题冲突，共谋解决办法。经过“教师讲解，初步了解，学生实践，合作探索，推理抽象，新知生成”的全过程，突出学生学习的主体地位，教师则是学生学习的组织者、引导者。学生的学习过程经历了“观察、实验、猜测、推理、验证”等活动过程，将知识点吃透、拿准。全课结束，学生好像在《西游记》的故事里漫游了一番，既有故事的趣味体验，又有数学知识的生成收获。这是教师比较有创意的一点。

2.现代化教学手段和传统教具相结合，相得益彰。

随着社会的不断发展，信息技术在课堂教学中发挥着愈来愈重要的作用。本节课，教师除了娴熟地运用了常规的教学课件，还使用了教学助手随堂直播的功能，呈现出别开生面的效果。同时，也没有抛弃传统。大家可以看到，教师发给学生的教具就是用普通的白纸制作而成，还有黑板上展示的词条，也是最简单的，我们笑称它们为“原生态”。虽然简单，但在我们的实际课堂中使用的频率高、效果好，而且能呈现出最真实的课堂。从学生反应来看，效果是很好的。学生很喜欢这样的学习活动，觉得有趣味，同时这样的处理，也节省出很多的教学时间。这看出教师有较强的驾驭信息技术的能力、灵活的头脑和卓越的智慧。

3.以学生为本，关注学生的学习状态。

每位教师对同样的教学内容，选择怎样的教学方法来进行教学设计，那就要“八仙过海，各显神通”了。但是，无论怎样去设计、去落实、去突破，最终都体现在学生身上。看学生是否学会，是否学得轻松、学得快乐。本节课中，学生对于知识的掌握还是比较牢固的，回答问题或者知识检测都比较顺畅，说明我们的知识目标已经达成。在学习的过程中，学生通过“看一看”“折一折”“分一分”“画一画”“说一说”“涂一涂”等形式进行学习，掌握了学习方法，完成了技能目标。学生在郭教师的调动下，保持着积极主动的学习态度，达到了情感态度的要求。而且，教师在教学中能注意到全体学生，保证学生的参与度，活动设置指向明确，环节衔接紧密，也保证了课堂的效率。

編辑∕韩晓雨