Numerical and Experimental Studies of the Acoustic Scattering from an Externally Ring-Stiffened Cylindrical Shell

ZHOU Fu-lin,FAN Jun,WANG Bin,TANG Wei-lin

(1.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai Jiao Tong University,Shanghai 200240,China;2.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Abstract:Studying the interaction of sound with double shells immersed in water is essential for improving existing underwater target detection and classification algorithms.To identify the key physics,a hybrid 2-D/3-D finite element modeling technique was employed to calculate and analyze the acoustic scattering from an externally ring-stiffened cylindrical shell.Approximate analytical expressions were explicitly derived to identify Bragg and Bloch-Floquet wave scattering in frequency-angle spectra.Monostatic scattering measurements were performed for validation.In contrast to the case of a plate,there are three kinds of elastic waves in a thin cylindrical shell：the flexural wave a0,compressional wave s0and shear wave T0.The flexural wave makes an important contribution to Bloch-Floquet wave scattering.The rings indirectly influence the exterior acoustic scattered field through the dynamic response of the shell,and serve as direct acoustic scatterers that increase the target cross section,especially at oblique incidence.For the external rings at an incident angle of 45°,the geometrical scattering is enhanced due to their influence as corner reflectors.Compared with the analytical method and physical acoustic method,the hybrid 2-D/3-D FE method considers the elasticity of structure,the occlusion and multiple scattering between the rib and the shell,and the interaction between the rib and the water.It has the advantages of high computing efficiency and accuracy,which is suitable for the structural-acoustic coupling analysis of complex stiffened structure in low and middle frequency.

Key words:acoustic scattering;cylindrical shell;external ring;finite element method

0 Introduction

Elastic cylindrical shells often occur as part of double-shell constructions and have been widely used in marine and aerospace research.Double shells are structurally connected to each other by common frames or rings which significantly affect the sound scattered by or radiated from the shells.Based on thin shell theory,Skelton(1992)[1-3]examined the sound scattering from two concentric cylindrical shells,in which the internal rings indirectly influence the exterior acoustic scattered field through the dynamic response of the shell.In target detection,a-coustic waves are easily transmitted through the outer shell to the interior,especially at low frequencies,and the waves are then scattered by the inner shell and the rings in the water area between double shells.In contrast to the inner shell,the outer shell can occasionally be neglected;thus,the externally stiffened shell becomes the main scatterer.Additional factors,including the coupling of water and rings,occlusion and multiple scatterings,remain to be considered[4].In this paper,the acoustic scattering from an externally ring-stiffened cylindrical shell is investigated as a simplification of double shells.

Numerical methods are generally used to calculate the structural-acoustic response of complex structures,such as the planar element method(PEM)based on the Kirchhoff approximation[5-7]and the finite element method(FEM)[8].Notably,the Kirchhoff approximation is applicable only for geometrical scattering at high frequencies[7].For the FEM,an efficient model with perfectly matched layers(PMLs)was proposed for calculating the radiation and scattering from axisymmetric objects[8].It is called the hybrid 2-D/3-D FE model and has been applied in ocean acoustics and scattering from complex objects[9-10].

In this study,the scattering characteristics of an externally ring-stiffened cylindrical shell are investigated.Chap.1 introduces hybrid 2-D/3-D FE modeling and presents a numerical calculation of scattering from an externally ring-stiffened cylindrical shell and a uniform shell for comparison.For the case of a finite periodically ribbed cylindrical shell,Chap.2 describes approximate analytical expressions to identify the elastic waves in the frequency-angle spectrum.Chap.3 analyzes the scattering characteristics of an externally ring-stiffened cylindrical shell.The results of a tank experiment are compared with the numerical solutions in Chap.4.Finally,conclusions are presented in Chap.5.

1 Hybrid 2-D/3-D finite element modeling

Considering a harmonic plane wave incident upon a thin cylindrical shell submerged in water,the incident wave is assumed to be parallel to the xOz plane with an incident angle θi(see Fig.1).The origin O is located at the center of the shell.The interior of the shell is in vacuo,and the ends of the shell are closed by flat endcaps.A set of rings is attached to the outside surface of the cylinder and seamlessly connected to the cylindrical shell.Therefore,the focus of the present research is the acoustic scattering of axisymmetric fluid-loaded structures subject to a nonsymmetric forcing field.The harmonic time dependence in eiωtwill be omitted.

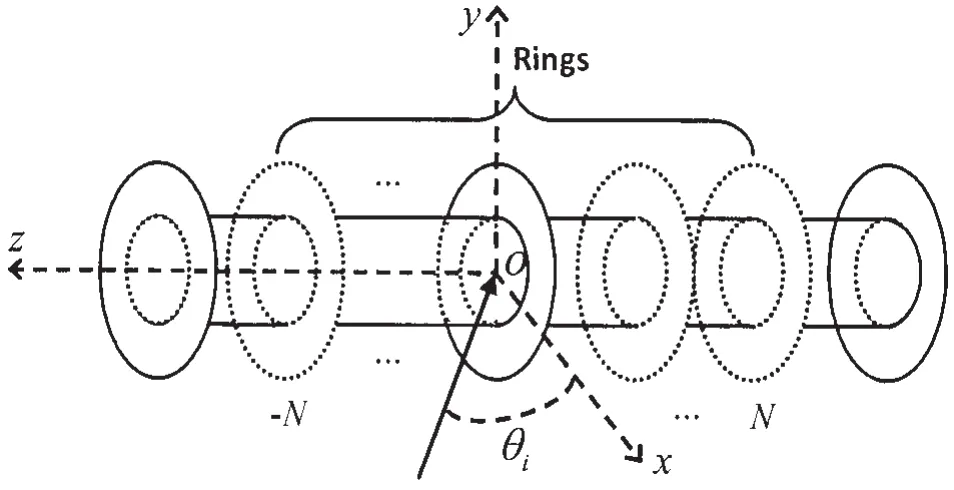
Fig.1 Schematic diagram of the externally ringstiffened cylindrical shell model

Considering Zampolli's method[8],the model superposition technique breaks the 3-D wave equations in the fluid and linear elastodynamic equations in the solid into Fourier series in cylindrical coordinates.The 3-D problem is decomposed into 2-D Fourier modal subproblems to solve the target scattering in the near field.A generic incident acoustic field pinccan be expressed in the following form：

where n represents the circumferential order and φ is the circumferential angle(0≤φ＜2π).Consistent with the decomposition of the applied load,the solid displacement （u,v, ）w and pressure p are decomposed in the same manner：

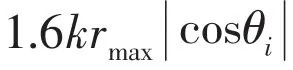
To simulate the free field,a Berenger PML with cylindrical coordinates is implemented in the azimuthal modal decomposition FE scheme[11].Next,the partial differential equations,the PML and the vibro-acoustic coupling boundary conditions are expressed in a weak form by the variational principle[12].To enable a solution via the FE scheme,these expressions are assembled into an algebraic form that includes a stiffness matrix and mass matrix.Finally,the FE model is built up and solved in the vibro-acoustic coupling module of the software COMSOL.

Next,the scattered pressure in the far field is calculated by using a 3-D propagation model.In accordance with the discrete form of the Helmholtz integral,the far-field pressure can be calculated as follows[10]：

where rijis the distance between the jth point on the surface S and the far field observation point i,with the surface normal pointing outwards from the surface S;（pj, dpj/dnj）denotes the scattered pressure as well as its derivative on the surface and Gijis the Green's function in the free field.Finally,the target strength(TS)takes the following form：

2 Approximate theoretical analysis

Considering an infinite thin cylindrical shell insonified by acoustic plane waves,in line with the consistency condition of the wave trajectory,the vibration of the cylindrical shell should be the traveling wave in the form of eiKzin the z-direction and symmetric in the circumferential direction for the circumferential angle φ.Thus,a general solution for the shell vibration can be expressed as follows：

where kφand K denote the circumferential and axial wavenumbers,respectively.Substituting Eq.(5)into the Donnell equations[13]for the displacements of the cylindrical shell yields the following equation containing the coefficient （u~,v~,w~）

The characteristic matrix is written as follows[13]：

The characteristic equation for elastic waves is given as follows：

which is used to solve the phase velocity of elastic waves.Unlike with a thin plate,three types of elastic waves might exist in a thin cylindrical shell because Eq.(8)has three solutions.They correspond to the flexural wave a0,compressional wave s0and shear wave T0.

At oblique incidence,the elastic waves in a cylindrical shell can be helical,and the corresponding wavenumbers are composited by the axial and circumferential wavenumbers：

The corresponding phase velocity is cph=ω/kl.The frequency dispersion curves shown in Fig.2(a)can be obtained by solving the characteristic equation.The detailed parameters for the calculation are presented in Chap.4.

Circumferential resonance occurs for helical waves when the azimuthal wave path equals an integer number of wavelengths,i.e.,kφ=n,where n=1,2,3….Based on the phase velocities of the elastic waves in Fig.2(a),the theoretical trajectories of the three types of circumferential waves are shown in Fig.2(b).

Fig.2(a)Phase velocities of three types of circumferential waves in an infinite cylindrical shell：flexural wave a0(red dot),compressional wave s0(black dashed-dot)and shear wave T0(blue solid)and(b)Their theoretical trajectories in the frequency-angle spectrum.Each family of curves is identified as follows：a0（n=27～3 2 ）,s0（n=1～ 4 ）and T0（n=1～ 4 ）

When the infinite cylindrical shell is stiffened periodically by rings,the Bloch-Floquet waves appear in the z-direction.Consistent with the Bloch-Floquet theorem[14],the wavenumber becomes the following：

where m=-∞,…,0,…∞ is the order of the Bloch-Floquet wave.The flexural waves can be scattered as a meridional leaky ray(in the z-direction)and then contribute to the Bloch-Floquet waves.Like a thin plate,the diagram of the flexural wave propagation is shown in Fig.3(a).The resonance condition of the Bloch-Floquet flexural wave scattering is the following：

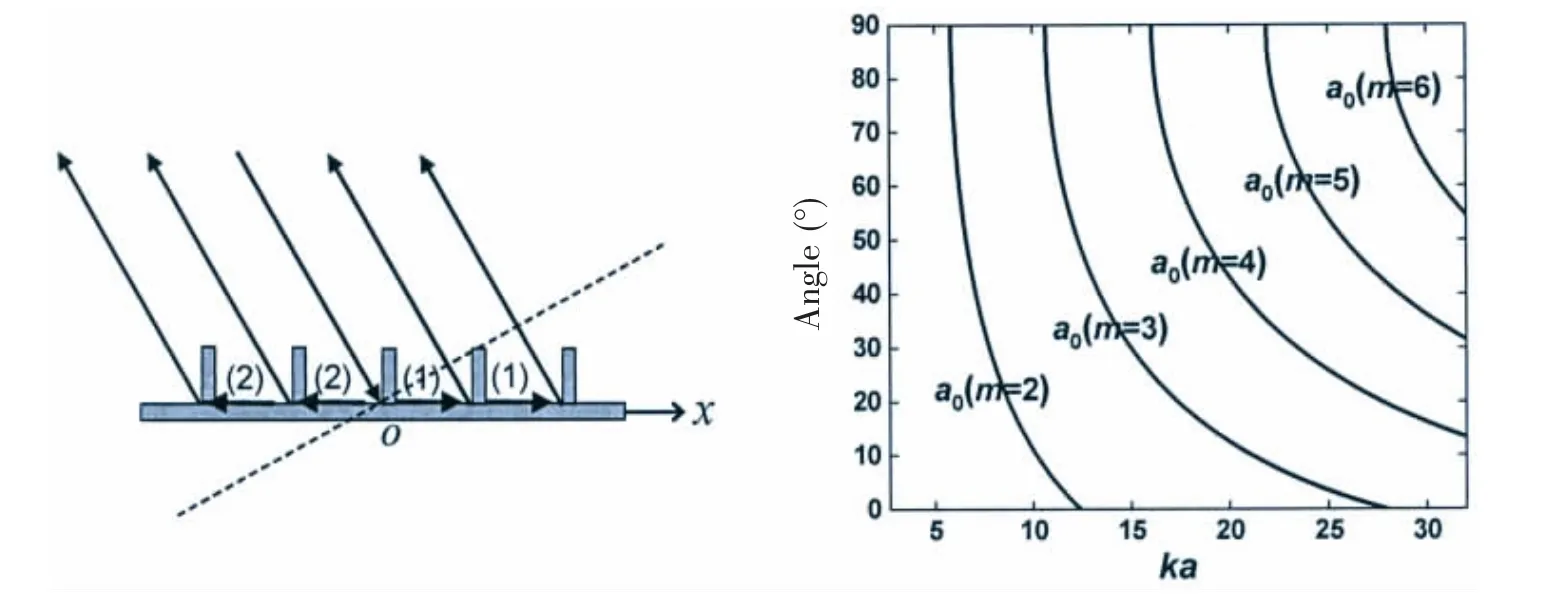
Fig.3(a)Diagram of the Bloch-Floquet flexural wave propagation[(1)forward and(2)backward]in an infinite stiffened cylindrical shell and(b)Its theoretical trajectories in the frequency-angle spectrum

where the symbols(‘+'and ‘-')represent the forward and backward BFWs,respectively,as shown in Fig.3(a).The Bloch-Floquet trajectories of the flexural waves are shown in Fig.3(b).

Notably,for the above approximate method,certain deficiencies could not be avoided：(i)the thin shell theory is not applicable to high frequencies;(ii)the detailed sizes and shapes of rings cannot be distinguished;and(iii)the radiation efficiencies of the three elastic waves are distinct but cannot be obtained here because of the neglected fluid loading.

3 Numerical analysis

Based on the above FE modeling technique and the approximate theoretical solutions,this chapter provides a numerical analysis of an externally ring-stiffened cylindrical shell.The externally ring-stiffened cylindrical shell used for the computations has similar parameters to those of Ref.[15].The shell has an outer radius a=3.12 cm,total length L=42 cm,thickness h1=1 mm,and ratios of h1/a=0.032 and a/L=0.149.The rings have a height H=1.3 cm,thickness h2=0.9 mm,and rib spacing d=2.1 cm.The elastic parameters are consistent with 304 stainless steel with E=191 GPa,σ=0.279 and ρ=7 570 kg/m3,and the corresponding longitudinal-wave velocity cLand transverse-wave velocity cTare 5 675 m/s and 3 141 m/s,respectively.The external fluid is water,with c0=1 470 m/s and ρ0=1 000 kg/m3.The dimensionless frequency range is 2.7＜ka＜32.0.

3.1 Helical waves

For a comparative analysis,the frequency-angle spectra of the TS for a uniform cylindrical shell and an externally ring-stiffened cylindrical shell are numerically calculated by using Eq.(4),as presented in Fig.4(a)and(b),respectively.The uniform cylindrical shell has no rings in comparison with the externally ring-stiffened cylindrical shell,but they have the same shell parameters.

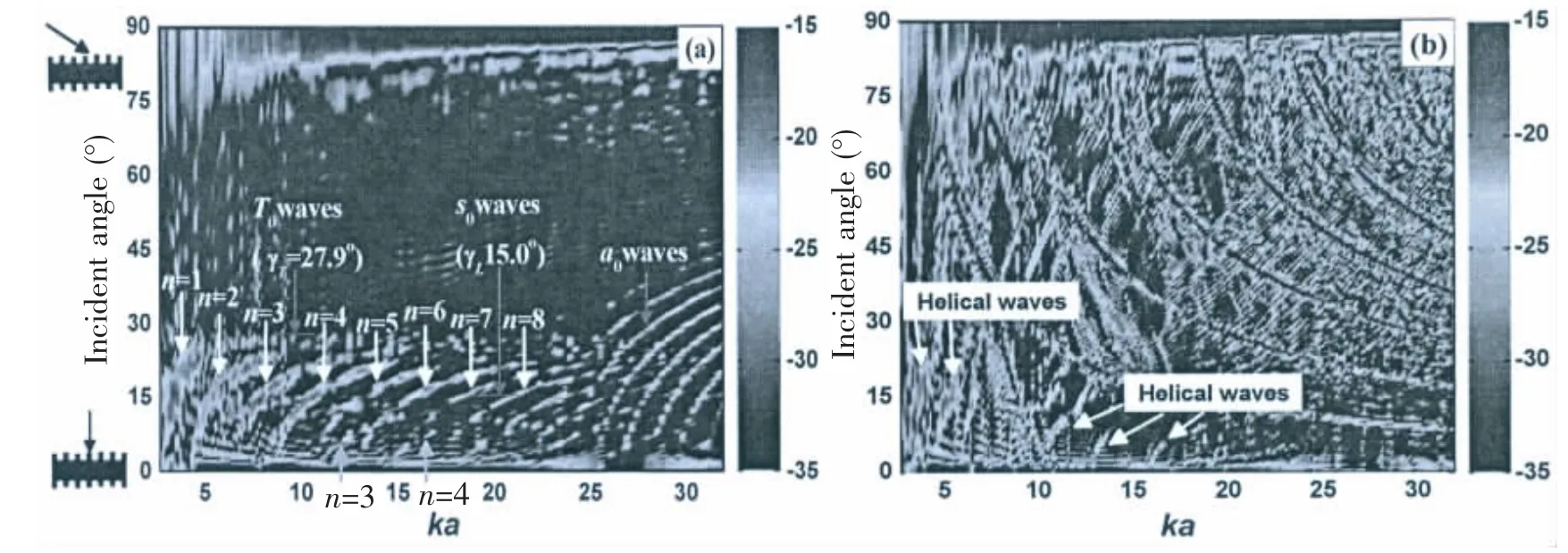
Fig.4 Numerical frequency-angle spectra of the target strength for(a)A uniform cylindrical shell and(b)An externally ring-stiffened cylindrical shell

In the response of the uniform cylindrical shell,bright arcs are prevalent near broadside incidence.Consistent with the circumferential resonance conditions(see Eq.(1)in Ref.[16]),these arcs are identified as the circumferential coupling loci for the helical propagation of the three elastic waves,as indicated in Fig.4(a).The compressional waves and shear waves,whose behaviors at low frequencies are similar to those in a plate,can be launched within the region from a broadside incidence to cutoff angles γL=sin-1（c0/ cL）=15.0°and γT=sin-1（c0/ cT）=27.9°,where cLand cTare the compressional and shear velocities in the shell material,respectively.High backscattering levels arise from the launching of helical leaky waves,which are reflected off the shell truncation and reradiated in the backscattering direction.The coupling loci for the a0and T0waves are more visible than those for the s0wave.Further,the bright arcs for the low-order T0waves are wider and stronger while those for s0waves are covered easily.Besides,for metal shells with external fluid loading,the a0wave is divided into two waves,namely,a0+and a0-.The a0+wave is similar to the a0wave,whereas an additional a0-wave is derived from the fluid loading and is also called the Scholte-Stoneley wave.Above the critical frequency corresponding to the sound speed in ambient fluid,a0+is a flexural and a0-a fluid-borne wave,and vice versa below the frequency[14].Further details on the scattering characteristics of helical waves in a finite cylindrical shell are discussed in Refs.[16-18].

Compared with the helical wave coupling loci in a uniform cylindrical shell,such as those in Fig.4(a),most helical waves become weak in Fig.4(b)for an externally ring-stiffened cylindrical shell because the helical propagation is blocked by rings.Near broadside incidence(0°-30°),helical waves at low frequencies(ka＜15)have more influence on the exterior scattered field than those at high frequencies(ka＞15).The bright arcs for the low-order T0waves are still visible.Additionally,many bright arcs appear in other regions.Considering previous studies on ribbed structures(e.g.,Refs.[3,14]),most of the waves are naturally considered to be generated via Bragg and BFW scattering,which will be discussed in the next section.

3.2 Bragg scattering and Bloch-Floquet wave scattering

To identify their trajectories,approximate theoretical solutions of Bragg and Bloch-Floquet scattering from an infinite ring-stiffened cylindrical shell are helpful.The same mechanisms exist for a finite cylindrical shell,with the only difference being the energy strongly scattered from the ends of the shell.According to the theoretical analysis in Chap.3,the bright arcs in Fig.4(b)can be identified as shown in Fig.5(a).

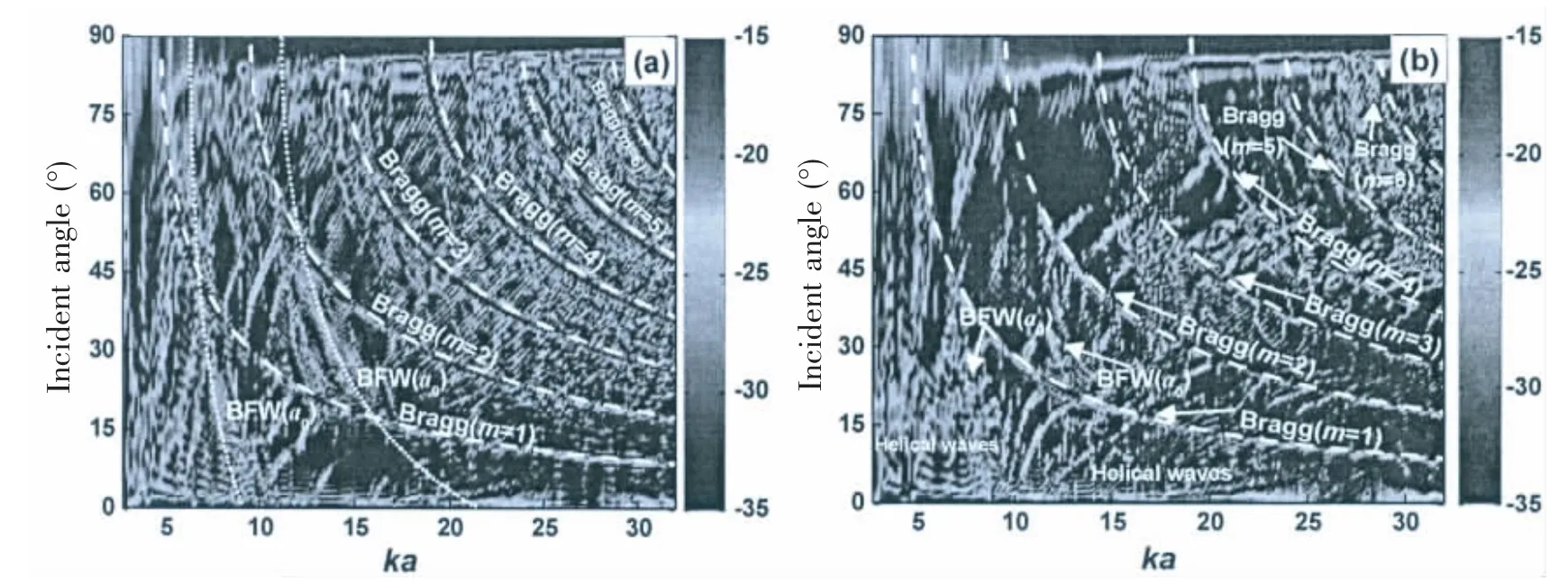
Fig.5 Numerical frequency-angle spectra of the target strength for(a)An externally ring-stiffened cylindrical shell and(b)An internally ring-stiffened cylindrical shell

First,Bragg scattering arises from the geometrical reflections of an incident wave on the inner and outer edges of the rings.These two parts have different arrival times,and their trajectories on the frequency-angle spectrum are consistent and can be evaluated as follows：

where k0is the wavenumber of the incident plane wave and d is the rib spacing.A number of marked bright arcs show excellent agreement with the theoretical Bragg trajectories of the first six orders.

Then,according to the theoretical trajectories in Fig.3(b),the Bloch-Floquet flexural waves with two low orders can be identified,as denoted as BFW （ a0）in Fig.5(a).The trajectories of flexural waves with high orders are more obvious than those with low orders.The same phenomenon occurs in the case of the internally ring-stiffened shell in Fig.5(b).In addition,according to the geometrical relationship of the ring height and ring spacing,sound waves are reflected by external rings and cannot be directly incident on the cylindrical shell when the incident angle is greater than 58°.Although the transmitted and diffracted waves can arrive on the cylindrical shell,the received echoes are weakened slightly.

According to the theoretical analysis in Chap.2,three types of elastic waves exist in the cylindrical shell.In the frequency-angle spectrum of the ring-stiffened shell,not all of the bright arcs can be identified for various reasons.Many factors make the scattering problem more complex,such as the coupling between the rings and the shell and the blocking or partition effect of rings on the surface helical waves.The rings transmit the coupling forces and moments to the shell and contribute to the dynamic response,which indirectly influences the exterior acoustic field.Moreover,external rings become direct elastic scatterers in water.

3.3 Effects of external rings

To identify the contributions of the external rings,an internally ring-stiffened cylindrical shell and an externally ring-stiffened cylindrical shell with a perfectly rigid surface are numerically modeled for comparison.Other parameters,such as the ring spacing,are the same for the both shells.For the quantitative analysis,the target strength as a function of the incident angle for the three models is shown in Fig.6.

Compared with the results for a uniform shell,the TS of the externally ring-stiffened shell is stronger as a whole and has more peaks at oblique incidence.These peaks are caused by the geometrical and elastic scattering from the rings,including the shielding effects and multiple scatterings between the rings and the shell.According to the frequency-angle spectrum in Fig.4(a),helical waves in the uniform shell can be labeled as HW in Fig.6(a)and(b),which appear in small incident angle range.

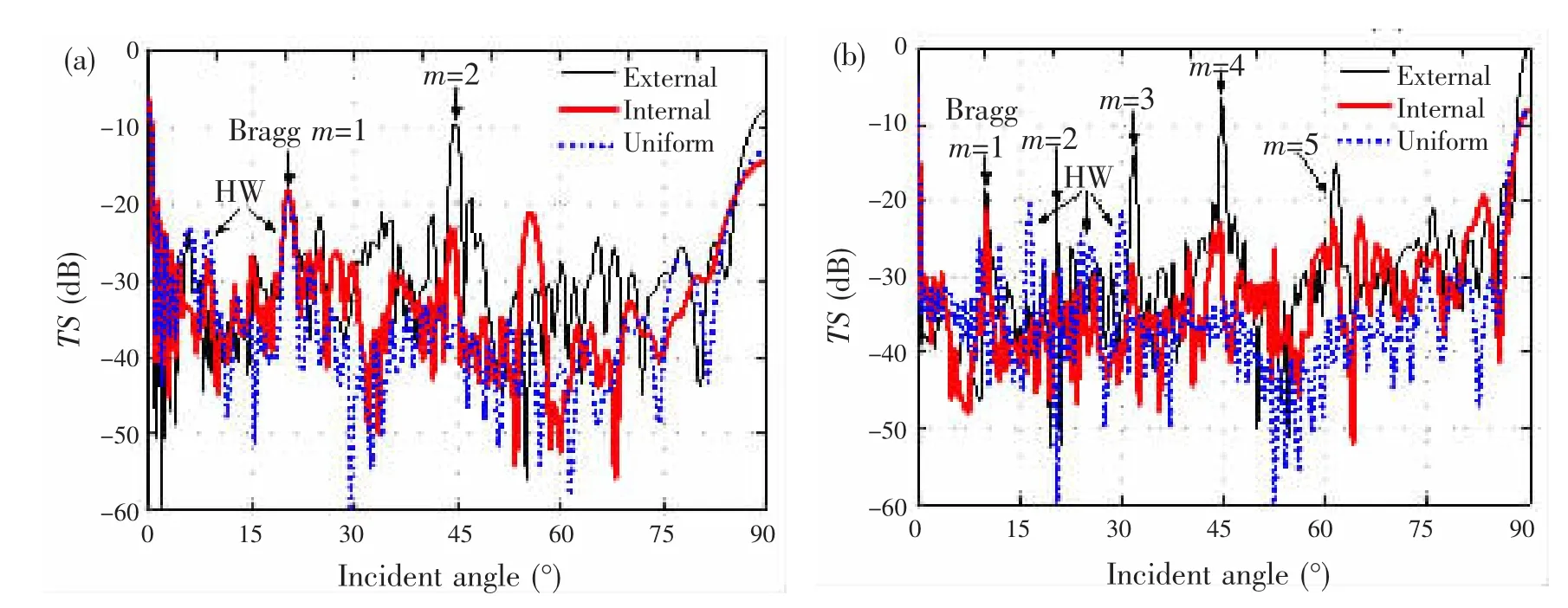
Fig.6 Comparison of the target strength for the backscattering of sound by an externally ringstiffened shell(black solid),an internally ring-stiffened shell(red solid),and a uniform cylindrical shell(blue dot)at(a)100 kHz(ka=13.3)and(b)200 kHz(ka=26.7)

For the two ring-stiffened shells,bright arcs of Bragg scattering from periodic rings are observed in Fig.5(a)and(b).Their peaks in Fig.6 are also labeled as Bragg orders.As expected,Bragg scattering from the external rings is generally stronger than it is from internal rings.The difference value of the TS between the two cases exceeds 10 dB at several incident angles and frequencies(e.g.,m=2～4 at 200 kHz).There are several reasons for this result.An external ring has two edges that directly reflect sound waves and contribute to strong Bragg scattering.For an internal ring,the incident waves need to be transmitted through the shell twice to encounter the ring,and thus more sound energy has to be consumed.From the aspect of mechanics,internal rings exert only forces and bending moments on the shell,thereby indirectly influencing the exterior scattered field.In addition to the indirect influence,the external rings as direct acoustic scatterers increase the target cross section,especially at oblique incidence.Moreover,a remarkable difference is observed in which the amplitude of the Bragg scattering from external rings increases progressively in the range of 0°-45°.In addition to the geometrical scattering,more peaks appear due to the elasticity of the rings,some of which are identified in Secs.4.1 and 4.2.Generally,the external rings enhance the target strength.

In addition,the TS of the externally ringstiffened cylindrical shell at 45°is less than those at broadside and end-on but much larger than those of the internally ring-stiffened and uniform cylindrical shells.This is because the external rings at 45°serve as corner reflectors and enhance the geometrical scattering,as shown in Fig.7.Furthermore,by comparing the average TS over the frequency band(20-240 kHz)of the three models,an enhancement near 45°is also observable for the case of the externally ring-stiffened cylindrical shell.

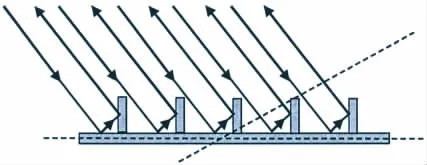
Fig.7 Corner reflector at an incident angle of 45°

4 Experiment

4.1 Experimental program and data processing

An experiment was conducted in an acoustic water tank with dimensions of 5×5×5 m3.The experimental configuration is shown in Fig.8.A ring-stiffened cylindrical steel shell was manufactured.In consideration of the limited space of the tank and the convenience of model machining,the length of the cylindrical shell is L=21 cm,and the other parameters of the material and geometry are presented in Chap.3.The trajectories of the Bragg scattering and Bloch-Floquet wave scattering are not changed.Considering the broad bandwidth of 20-240 kHz(ka=2.7-32.0),we employed four transducers with bandwidths of 20-40 kHz,40-80 kHz,60-120 kHz,and 120-240 kHz.Tab.1 summarizes their specifications.Each transducer outputs a linear-phase finite impulse response(FIR)signal.A standard Teledyne RESON hydrophone(TC4014)was used,and its sensitivity is-186 dB±3 dB re1V/μPa over the frequency range 15 Hz to 480 kHz.The whole experimental spectra were completed by overlapping and stitching together the four slices of data.

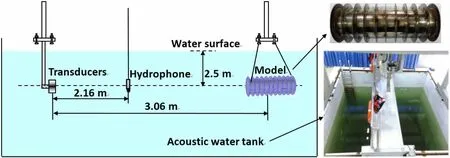
Fig.8 Experimental configuration

Tab.1 Specifications of the four transducers used in the tank experiment

To obtain the full-azimuth scattering characteristics,the model was automatically rotated in the horizontal xOz plane by drivers at a rotational speed of 60°/min.Continuous data acquisition was achieved in a time interval of 0.5 s to ensure adequate resolution of the experimental spectra and avoid measurement errors from the model's waggle to the greatest extent possible.Having obtained the direct waves and reflections from the model through appropriate time windows,we performed an FFT on the time signals for each incidence angle to obtain the experimental frequency-angle spectrum.

4.2 Experimental analysis

Based on previous data processing methods,the experimental frequency-angle spectrum of the externally ring-stiffened cylindrical shell is shown in Fig.9(a).For comparison,the simulated result of a model with the same size is shown in Fig.9(b).The scattering characteristics of the simulated and experimental results are generally consistent.Distinct highlights are observed in both figures that are consistent with the theoretical Bragg scattering trajectories of the first six orders in Fig.4.According to the theoretical Bloch-Floquet condition,we identi-fied the experimental spectrum,as labeled in Fig.9.Some highlights in the experimental spectrum are ambiguous because of the relatively weak echoes from rings and the low signal-tonoise ratio.

Fig.9 Frequency-angle spectra of the externally ring-stiffened cylindrical shell(a)Experiment and(b)Simulation

5 Conclusions

A hybrid 2-D/3-D finite element modeling technique was employed to investigate the scattering characteristics of an externally ring-stiffened cylindrical shell.For a contrastive analysis,relevant FE models were also designed,including a nonribbed model and an internally ring-stiffened model.To identify the Bragg and Bloch-Floquet trajectories in the frequencyangle spectra,approximate analytical expressions for a periodically ring-stiffened cylindrical shell were derived.The combination of the hybrid FE model and the approximate solution revealed different aspects of the physics driving the target response.

The effects of external rings and the structural elasticity on scattering were analyzed by comparison with a uniform elastic FE model and a perfectly rigid FE model.In addition to the indirect influence of the forces and bending moments on the shell similar to internal rings,the external rings in water act as direct acoustic objects that increase the target cross section,especially at oblique incidence.For the external rings at 45°,the geometrical scattering is greatly enhanced via their influence as corner reflectors.

The validity of the hybrid FE models of the externally ring-stiffened cylindrical shell was confirmed by comparing the simulated frequency-angle spectrum with the monostatic scattering measured data.The Bragg and Bloch-Floquet trajectories were generally consistent,and any discrepancies might arise from the effects of the external rings.Some highlights in the experimental spectrum are ambiguous because of the relatively weak echoes from the rings and a somewhat low signal-noise-ratio during the measurement.

Acknowledgements

We thank Dr.Peng Zilong and Dr.Tong Yunzhe for their helpful discussions.We also appreciate the help of Xu Kai,Dr.Zhao Kaiqi and Dr.Liu Bo in performing the tank experiments.