Research on the Design and Parameter Influence Law of A High-Static-Low-Dynamic Stiffness Vibration Isolator Using for Marine Equipment
2019-07-08YANGZhirongWANGYanKEXianyongRAOZhushi
YANG Zhi-rong,WANG Yan,KE Xian-yong,RAO Zhu-shi
(1.Marine Engineering Institute,Provincial Key Laboratory of Naval Architecture&Ocean Engineering,Jimei University,Xiamen 361021,China;2.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University,Shanghai 200240,China)
Abstract:A vibration isolator consisting of circular plate and linear spring with High-Static-Low-Dynamic Stiffness(HSLDS)is introduced.The buckling modes of the circular plate are analyzed by using analytical method and FEM respectively,and the results show that the analysis of analytical method is coincided with FEM analysis.Furthermore,the HSLDS characteristic of the vibration isolator is calculated and verified by using ANSYS software.Finally,a nonlinear mathematical model of HSLDS vibration isolator is developed and its amplitude-frequency characteristic is further analyzed by using the Increment Harmonic Balance(IHB)method,and the influence law of the system parameters on it is analyzed.The analysis results show that the stiffness ratio is a factor related to the type and degree of nonlinearity.Moreover,the HSLDS vibration isolator presents the typical jump phenomenon of the Duffing oscillator of amplitude-frequency characteristic.
Key words:high-static-low-dynamic stiffness;vibration isolator;marine equipment;FEM
0 Introduction

In this paper,firstly,a simple and reliable structure of a vibration isolator with the desired nonlinear stiffness is presented.Secondly,the buckling mode of the circular plate is analyzed by using analytical method and FEM,respectively.Thirdly,the HSLDS characteristic of the vibration isolator is calculated by using ANSYS software,which the first step of the buckling mode of circular plate is used to initial the outline of circular plate.Finally,the amplitude-frequency characteristic of the HSLDS vibration isolator and the influence law of the system parameters on it are analyzed.
1 Structure of vibration isolator with HSLDS
It is required to develop HSLD stiffness isolators with minimum number of elements,preferably with only one that provides the best simplicity,and thus high reliability.The structure of HSLDS vibration isolator is shown in Fig.1.It consists of the prestressed circular plate and the linear spring.The pre-stressed circular plate acts as the negative stiffness while the linear spring acts as the positive stiffness.The HSLDstiffness is obtained by connecting the circular plate and the linear spring in parallel while the weight of the isolated object is sustained by the linear spring.The structure of designed vibration isolator is simple and reliable.

Fig.1 The structure of HSLDS vibration isolator
2 Analytical and FEM analysis of HSLDS vibration isolator
2.1 Analytical analysis of the buckling modes of circulate plate
The circulate plate suffered from the pressure in the periphery is shown in Fig.2,where R represents the radius of circulate plate;Pris the pressure in the periphery;t is the thickness of the circulate plate.The motion equation of circulate plate suffered from the pressure can be obtained by using cylindrical coordinates as follows:


Fig.2 The circulate plate suffered from the pressure in the periphery


Substituting Eq.(2)into Eq.(1),we can get the equation as follows:

The Eq.(3)is the governing equation of the buckling problem of circular plate.The radial displacement of circular plate W can be supposed in the following form:

when n=0,the buckling mode of circular plate is symmetrical.However,it is dissymmetrical while n gets with other values.
Substituting Eq.(4)into Eq.(3),the equation can be rewritten as follows:



The general solution of Eq.(6)can be written as:

where C1,C2,C3,C4are arbitrary constant,Jn(x ) and Nn(x ) are the first and second kinds of n-order Bessel function respectively.Owing to the internal force and deflection of the center of circular plate are finite,the constants C2,C4should be equal to zero,otherwise Nn(x)and x-nwould be infinite when r=0(namely x=0).So the Eq.(4)can be written as follows:

Supposing the boundary condition of circular plate is simply support at r=R,and then the expressions can be obtained as follows:

Substituting Eq.(8)into Eq.(9),Eq.(9)can be rewritten as follows:

The recursion formulas of Bessel function are:

The determinant of coefficients matrix of Eqs.(10)-(11)is equal to zero,so we can get eigen value equation as follows:

If n=0,the Eq.(14)can be rewritten as follows:

when ν=0.3,the minimum solution of above equation is αR=2.05,so the critical press of the circular plate is:

If n=1,and ν=0.3,the minimum solution of Eq.(14)is αR=3.63,so the critical press of the circular plate is:

Example calculation:The parameters of circular plate are R=260 mm,t=1 mm,E=200 GPa,ν=0.3,substituting them into Eqs.(16)-(17),the first and second steps of buckling mode values can be calculated as follows:Pr1=142 239 Pa;Pr2=447 036 Pa.
2.2 FEM analysis of the buckling modes of circulate plate
The buckling modes of circulate plate can also be calculated by using the FEM.It can give the initial disturbances to the plate for calculating the nonlinear buckling analysis which can verify the HSLDS characteristic of the vibration isolator.The FEM model of circular plate with above geometry parameters in section 2.1 was built by using ANSYS software.Moreover,the boundary condition of circular plate is supposed with simply support r=R.The first and second steps of buckling modes of circulate plate are shown in Fig.3 and Fig.4 respectively.
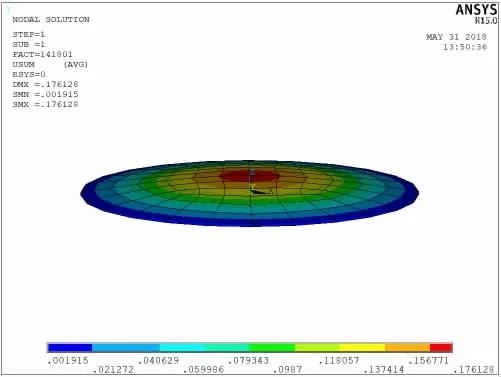
Fig.3 The first step of buckling mode of circular plate

Fig.4 The second step of buckling mode of circular plate
It can be seen that the first step of buckling mode value is Pr1=141 801 Pa and the second step of buckling mode value is Pr2=468 156 Pa.The results are coincided with the above analytical analysis results.
2.3 FEM analysis of the HSLDS characteristic of the vibration isolator
In order to verify the HSLDS characteristic of the vibration isolator shown in Fig.1,the FEM model of the isolator was built by using the ANSYS software as shown in Fig.5.The parameters of circular plate are R=260 mm,t=1 mm,E=200 GPa,ν=0.3;and it connected with a linear spring,for which the stiffness is k=10 N/mm.The boundary condition of circular plate is simply supported and the base of linear spring is restrained.The first step of the buckling mode of circular plate shown inFig.3 was used to initial the outline of circular plate to calculate the nonlinear buckling analysis,for which the arch height of the center of circular plate is about 8.7 mm.The center of the circular plate is applied with static force F=1 000 N.The results of nonlinear buckling analysis are shown in Fig.6 and Fig.7.

Fig.5 The FEM model of vibration isolator

Fig.6 The relationship between the force and the displacement of isolator

Fig.7 The relationship between the stiffness and the displacement of isolator
It can be seen that for the elastic system with a flat area on its force characteristic the displacement is increasing while the force remains unchanged.Namely that is an area with stiffness close to zero as shown in Fig.7.Moreover,it can be obtained from the figures that the force is about cubic displacement and the stiffness is about quadratic displacement.The structure of vibration isolator designed in this paper was verified with HSLD stiffness on the force characteristic.It would have great potential in vibration isolation as it is easy and reliable in application.
3 Amplitude-frequency characteristic of the HSLDS vibration isolator
3.1 Amplitude-frequency characteristic
The HSLDS vibration isolator can be simplified as one-degree-freedom vibration isolation system with the elastic restoring force is nonlinear as shown in Fig.8,which is different from the linear isolator system.As shown in Fig.6,the relationship between the force and the displacement is cubic,the elastic force of the HSLDS isolator can be written as follows:

where y is the displacement of isolated object,k is the stiffness of the linear spring,and a is the coefficient given from Fig.6,which is related to structure of isolator.When the system is suffered from the harmonic excitation force F=F0cosωt,the dynamic equation of the system can be written as the Duffing equation:


Fig.8 The simplified system for HSLDS vibration isolator
where m and c denote the mass and damper,respectively.For simplicity in the mathematical formulation,the following dimensionless parameters are introduced:

Substituting Eq.(20)into Eq.(19),one obtains:


where A is the response amplitude,and θ is the phase angle.Substituting Eq.(22)into Eq.(21),the equations can be obtained by using the increment harmonic balance(IHB)method as follows:

By eliminating θ,one obtains:

The Eq.(24)gives the relationship between the response amplitude and the excitation frequency.Substituting the parameters into Eq.(24)with f=1,γ=-0.1,0,0.1,and ζ=0.04,the diagram of amplitude-frequency characteristic can be obtained as shown in Fig.9.

Fig.9 The diagram of amplitude-frequency characteristic of HSLDS isolator
It can be seen that the diagram of amplitude-frequency characteristic of HSLDS isolator system is different from the linear vibration isolator system.Note that γ is a factor related to the type and degree of nonlinearity.When γ<0,the FRF curve bends to the left,marking a softening behavior.When γ=0,the system becomes linear and the FRF assumes its standard shape with a peak at Ω=1(when damping is small).Finally,when γ>0,the plot leans over to the right because of its hardening characteristic that is the amplitude-frequency characteristic of the HSLDS isolator introduced in this paper.Moreover,it presents the typical jump phenomenon of the Duffing oscillator.As the frequency is increased the amplitude increases follow-ing the upper or resonant curve.At the frequency Ωd,marked with the letter D,it suddenly drops to the lower or non-resonant branch.Similarly,decreasing the frequency,the response follows the non-resonant branch until the frequency Ωu,marked with the letter U.A further decrease in frequency causes the response to jump up to the resonant branch.
3.2 Effects of the system parameters
In order to investigate the effect of different damper ratios on the amplitude-frequency characteristic of HSLDS isolator,the damper ratios are given with different values ζ=0.02,0.04,0.06,0.14 while other parameters remain unchanged with f=1,and γ=1.The diagram of the amplitude-frequency of isolator is shown in Fig.10.It can be seen that the amplitude is decreasing with the increasing damper ratio.So the resonant peak can be attenuated by increasing the damper ratio and the main resonant frequency can be reduced.When ζ>0.3,the jump phenomenon of the Duffing oscillator has disappeared.
Also the stiffness ratios are given with different values γ=0,0.05,0.5,1 while other parameters remain unchanged with f=1,and ζ=0.04.The diagram of the amplitude-frequency of isolator is shown in Fig.11.It can be seen that the FRF curve bends to the right more deeply as the stiffness ratio increasing.Furthermore,the amplitude at resonant peak is decreasing and the resonant frequency is increasing as well.It can be inferred that the stiffness ratio γ is related to the degree of nonlinearity.The larger value of stiffness ratio the stronger in nonlinearity and the isolator looks like more‘hardening'.

Fig.10 The effect of damper ratios on amplitudefrequency characteristic
Finally,the excitation force ratios are given with different values f=0.05,0.5,1,1.5 while other parameters remain unchanged with γ=1,and ζ=0.04.The diagram of the amplitude-frequency of isolator is shown in Fig.12.It can be seen that the amplitude peak is increasing as the excitation force is increasing.It is similar to the linear isolator system.If the excitation force tends to zero,the response amplitude would be zero.

Fig.11 The effect of stiffness ratios on amplitudefrequency characteristic
4 Conclusions

Fig.12 The effect of excitation force ratios on amplitude-frequency characteristic
A novel HSLDS vibration isolator using for shipping was proposed in this paper.The buckling modes of the circular plate were analyzed by using analytical method,and are coincided with FEM.Furthermore,the HSLDS characteristic of the vibration isolator was calculated and verified,showing that the structure of isolator proposed in this paper is reasonable and reliable.Finally,a nonlinear mathematical model of HSLDS vibration isolator was developed.The amplitude-frequency characteristic analysis results show that the stiffness ratio is a factor related to the type and degree of nonlinearity,the larger value of stiffness ratio the stronger in nonlinearity and the isolator looks like more‘hardening'.Moreover,the HSLDS isolator presents the typical jump phenomenon of the Duffing oscillator.The amplitude peak is increasing as the excitation force is increasing.However,the resonant peak can be attenuated by increasing the damper ratio and the jump phenomenon may disappear by the large damper ratio.
Acknowledgements
This work is supported by the Planned Science and Technology Project of Xiamen Municipality(Grant No.3502Z20183033);Research Project of State Key Laboratory of Mechanical System and Vibration(MSV201901);Key Disciplines Laboratory for National Defense for Ship Equipment Noise and Vibration Control Technology,Shanghai Jiaotong University;and Key Science and Technology Projects of the Ministry of Transport of China(2018-MS2-058).
杂志排行
船舶力学的其它文章
- Numerical and Experimental Studies of the Acoustic Scattering from an Externally Ring-Stiffened Cylindrical Shell
- Strength Assessment of Damaged Tubular Bracing Members after Impact in Offshore Structure
- Experimental Investigation on Dynamic Behavior of Porous Material Sandwich Plates for Lightweight Ship
- A New Scheme for Vortex Sheet Diffusion in Fast Vortex Methods
- LQR Control of a Three Dimensional Underwater Glider
- Research on the Mechanism and Characteristic of Added Resistance of Moonpool with Recess
