A New Scheme for Vortex Sheet Diffusion in Fast Vortex Methods
2019-07-08GUXinzhongLIShunming
GU Xin-zhong,LI Shun-ming
(1.College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.Department of Vehicle Engineering,Nanhang Jincheng College,Nanjing 211156,China)
Abstract:Following Ploumhans,a fast vortex method was developed for the analyses of three-dimensional unsteady flow.A new diffusion method is proposed for the vorticity creation close to a 3D body surface,in which a number of vortex particles are introduced into the flow field to satisfy the nonslip boundary condition on the boundary.An adaptive Fast Multipole Method(FMM)is used for velocity and its gradient computing to achieve high accuracy at a reasonable cost.The new scheme is applied to the simulations of starting flow around a sphere at Re=300 and 500 for investigating the feasibility.
Key words:vortex methods;vortex sheet diffusion;adaptive fast multipole method;unsteady flow
0 Introduction
In the past three decades,the vortex methods have been developed and been applied to the analysis of complex,unsteady flows.Leonard and Chua proposed the application of simulations for interaction between interlocked vortex rings and between two colliding vortex rings[1].Mas-Gallic[2]presented an accurate method to simulate viscous effect by using the particle strength exchange scheme.Mansfield et al[3]simulated the collision of coaxial vortex rings by using Lagrangian vortex element methods integrated with a dynamic eddy viscosity model.Baoshan et al[4]used the 2D vortex-boundary element method to simulate the unsteady im peller-diffuser interaction in a diffuser pump.Fukuda et al[5]calculated the inclined collision of a pair of vortex rings by using vortex method,with a redistribution model of core spreading method.
For a practical computation,the number of vortex particles has to increase due to the requirement of higher resolution of turbulence structures.And it will lead to the computational time and storage cost increase drastically.To solve this problem,Koumoutsakos et al[6]and Winckelmans et al[7]introduced the fast multipole method(FMM)into the vortex methods,while Fernandez et al[8]and Ploumhans et al[9]enhanced the computation speed with the parallel computation technique.
Many of those works have made the vortex methods applicable to high-resolution simulations of flow with viscous boundaries.Kamemoto and Ojima[10-11]applied the vortex method to the simulation of flow around a moving human body and a swimming fish.
In this paper,we presented a new scheme for vortex particles creation in the vicinity of the body coupled with the adaptive fast multipole method,for further improving the computation speed and enhancing the calculation efficiency.
1 Viscous vortex methods
1.1 Basic formulas
Three-dimensional incompressible flow is governed by the vorticity equation:

where u( x, )
t is the velocity vector,ν is the kinematic viscosity and ω=▽×u is the vorticity.
In viscous vortex methods,the vorticity field is represented by a set of Gaussian smoothing vortex particles.
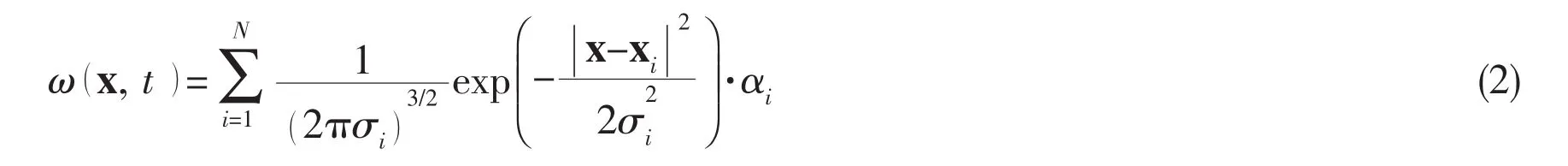
where xi,αiand σidenote the position,strength and smoothing parameter of particle i.
In order to satisfy the nonslip boundary condition on solid surfaces,a Dirichlet condition on the normal component of ω states that the tangential derivative of the velocity is zero at the solid boundary,

And the Neumann conditions on the tangential components of ω express the cancellation of the slip velocity at the wall.The velocity can be written as:

where U∞is the free stream velocity and ψ is the stream function.The relationship between ψ and ω is as follows,

1.2 Numerical implementation of the method
The vortex method described above is implemented essentially in following stages:
(1)Computing the local velocity u and its gradient▽u follows from the Biot-Savart law.

This is done efficiently by using the adaptive FMM and will be discussed in another section below.
(2)Convecting all the particles and changing their strength according to the following formulas.

The first term of right-hand side of Eq.(8)represents the contribution from particle stretching,and the second one involves the strength exchanging due to viscous diffusion.
(3)After the vortex particles'convection and strength exchange,there is a slip velocity Uslip,induced by the free stream and by all vortex particles at the solid surface.Here we assume that a laminar boundary layer is created over the surface due to the Uslip.Once the slip velocity has been determined,the boundary layer is divided into a set of vorticity layers and then replaced by equivalent discrete vortex particles.
(4)Direct application of the vortex dynamics yields the force F acting upon a body,approximating to the time derivative of the linear impulse[12]:

where ρ is the density and V is the volume occupied by the fluid.Then the force coefficients can be obtained:

(5)To keep overlap among vortices,the old particles must be replaced by new ones on a regular lattice every few steps.
2 Adaptive FMM
The original FMM enables calculation of long-ranged force in the n-body problems with high accuracy for an acceptable cost[13].The new version FMM in three dimensions is applicable to compute pairwise interactions between massive particles[14].Now,this method is used to compute the induced velocity of vortex particles.(Fig.1)
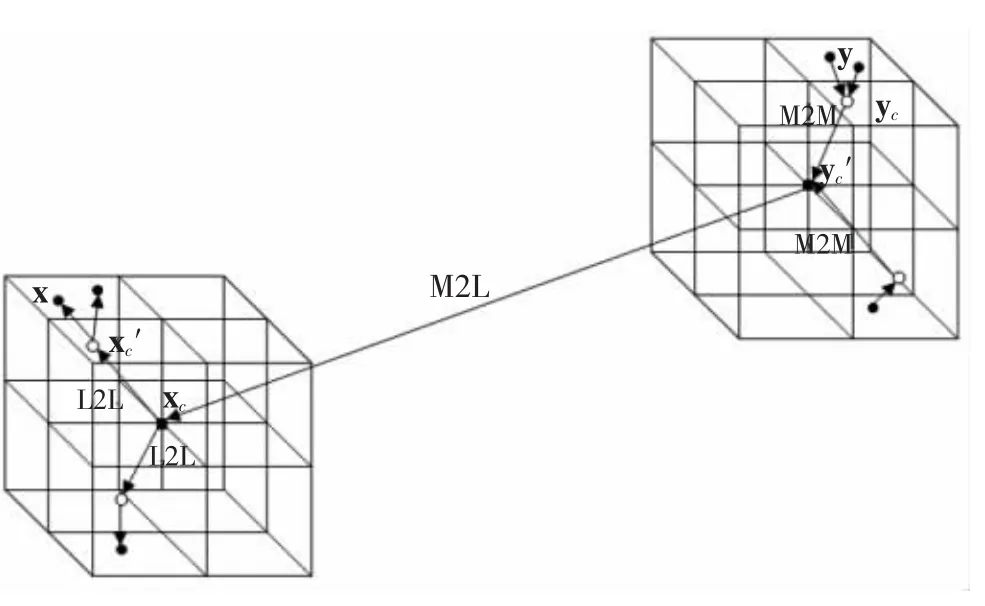
Fig.1 Fast multipole algorithm
In this section,the basic FMM formulas are listed,which will be used to implement the adaptive FMM.And the more detailed discussion can be found in Ref.[14].
2.1 Basic FMM formulas
The local velocity without smoothing function at x can be expanded as:


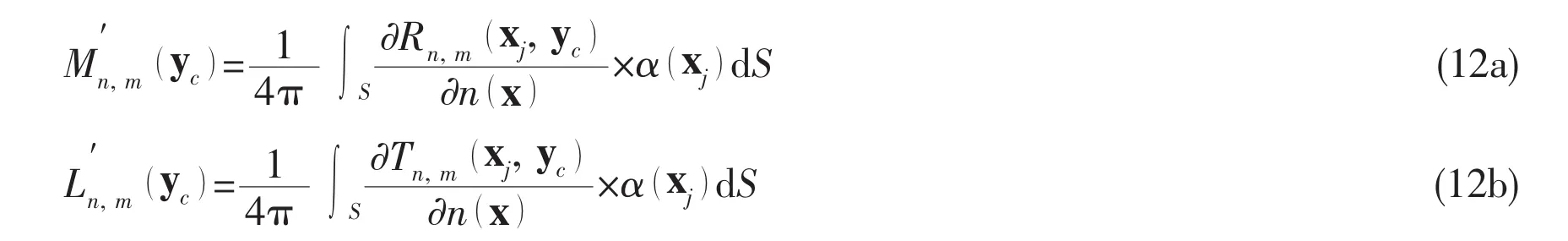
The functions Sn,m,Un,m,Rn,mand Tn,mare solid harmonic functions[15].And the multipole expansion center can be shifted from ycto yc′according to the M2M translation:
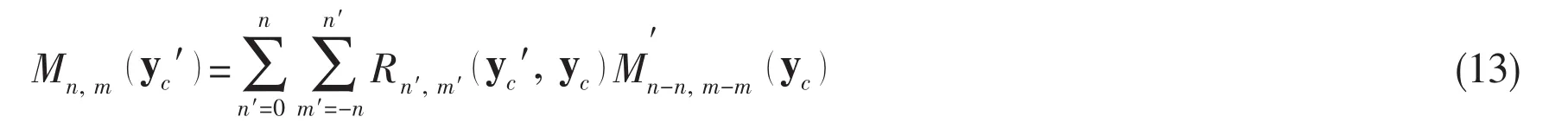
The multipole moments can be translated to the local expansion coefficients using the M2L translation:

In the new FMM formulations,the multipole expansions can also be translated to local expansions via the exponential expansion.Then velocity at x can be computed by

where S(ε) is determined by the required accuracy,αm,k=2πm/Mk,d is the cube length.And Wk,mis the exponential expansion coefficients,can be obtained from multipole moments using the M2X translation,
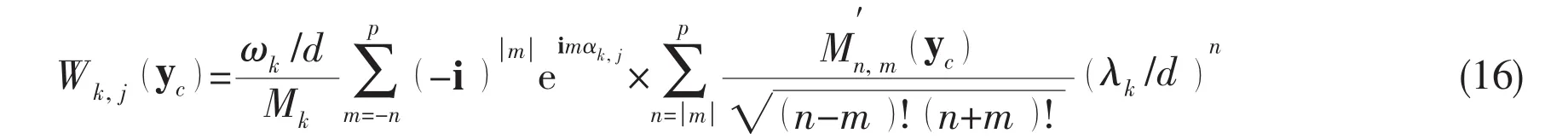
where ωkis the weight,λkis the node and Mkis the integer array.The exponential expansion center is then shifted from point ycto point x1according to X2X translation:

Then,the coefficients for local expansion centered at x1can be obtained from the exponential expansion using X2L translation:
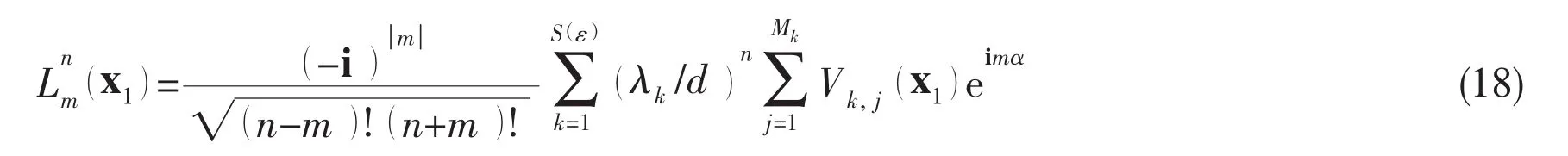
The local expansion centered at x1can be translated to x1′using the L2L formula:
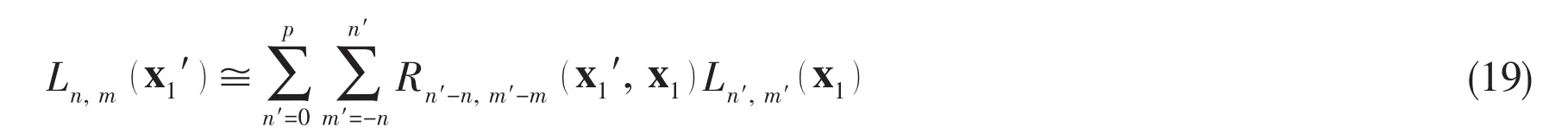
2.2 Adaptive FMM
An adaptive FMM,based on the diagonal form translation and adaptive tree structure,enables accurate representation of a complex shape bluff body and can adapt to the changing of computation domain.Thus,it is suitable to vortex particle simulation.However,little such research has been conducted before.To address this gap,this study focuses on the efficient computation of velocity field and its gradient with the adaptive FMM.
To run the algorithm,a hierarchical tree of boxes is constructed by dividing the 3D computational domain(a box containing all boundary elements and discrete vortices)into smaller and smaller sub-domains[15],as shown in Fig.2.
For each box b on level l(l≥2),four interaction lists are defined as indicated in Fig.3.To perform M2X and X2L translations,boxes in list 2 need to be further divided into six sublists associated with six coordinate directions[16].
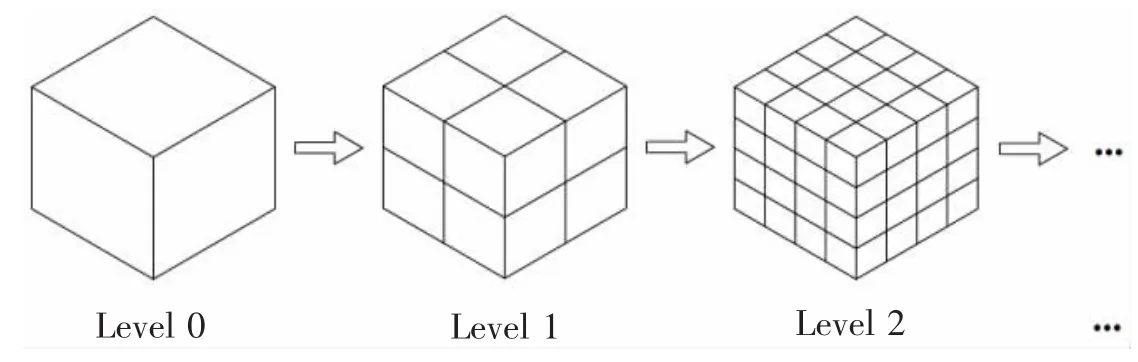
Fig.2 The tree structure
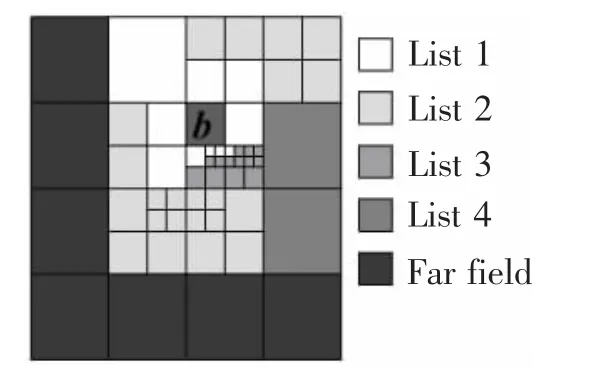
Fig.3 Four lists associated with box b
Adaptive FMM Algorithm is as follows:
(1)Initialization
Choosing calculate precision ε,the order of the multipole expansions p and the maximum number s of vortex particles allowed in a childless box.
(2)Step 0
Loading the data files,defining the initial computational domain and building the adaptive tree structure.
(3)Upward pass
For each childless box b,calculating multipole moments at its center from all vortex particles in b according to Eq.(12a).Recursively move the moments from b's center to its parents'using M2M(Eq.13).Then,a pth-order multipole expansion is generated for each box b at its center,representing the contribution from all the vortex particles in box b to particles in its list 1 and 3.
(4)Downward pass
Step A:Starting from level 2 to the lowest level:
(a)For each box b,if it contains more than p2particles,generate a local expansion at its center from all vortex particles in its list 4 boxes using Eq.(12b).Otherwise,directly valuate the induced velocity at each particle point according to Eq.(6).
(b)For each box b,translate the multipole moments of b to the local coefficients of box c in list 2 of b using M2X,X2X and X2L.
(c)Translating local coefficients of box b to the local coefficients of b's children using L2L translation.
After the sub-step A,local coefficients for each childless box are formed and added together,which can be used to calculate the velocity and its gradient.
Step B:
(a)For each childless box b,calculate the velocity of each particle contained using local expansions,according to Eq.(11b).
(b)For each childless box b,directly compute the velocity at each particle point due to all particles in b's list 1 boxes using Eq.(6).
(c)For each box childless b,if the number of particles contained is greater than p2,calculate the velocity field by using multipole expansions of b's list 3 boxes using Eq.(11a).Otherwise,directly valuate the velocity at each particle point according to Eq.(6).
3 Vortex sheet diffusion
There are many numerical procedures simulating vortex sheet diffusion in vortex methods.The most widely used one,named Particle Strength Exchange(PSE)method,is performed by a kernel technique[17].Although the convergence of this method has been proved and its accuracy has been investigated[18-19].The PSE method has some disadvantages in practice:it is generally time-consuming to calculate the strength of vortex panels by solving the boundary integral equations;the circulation of particles is not always conservative for complicated geometries.Therefore,we propose a much simpler and more efficient method for vortex particles creating on the solid surface.
3.1 Introduction of vortex sheets
In vortex methods,the surface of the solid body is discretized by a number of computational panels with initial strength γ,determined by the free stream and by all vortex particles.Obviously,after the vortex particles'convection,stretch and diffusion,a slip velocity is presented on the body surface.The variation of panel strength Δγ caused by the slip velocity will result in a vorticity flux near the surface.To simulate the diffusion process,the vorticity is emitted into the flow by properly distributing of vortex particles in the vicinity of the body in present method.
For simplification,the slip velocity is considered to be uniform over each panel here.Sup-posing further that all the vortex particles are created(due to slip velocity)in a laminar boundary layer over the flat computational panels.If assuming the velocity of potential flow is constant,the boundary-layer equations can be simplified to[20]:

With the boundary conditions

where u and v denote the velocity in the x and y direction,respectively.By introducing a new similarity variable η,we finally get the single ordinary differential equation,

And the boundary conditions are given in term of η as:

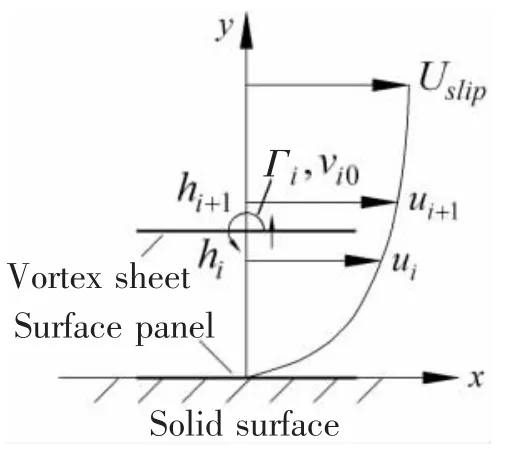
Fig.4 Introduction of vortex sheets
The flow field is considered to be two-dimensional for convenience.The boundary layer is divided into n sub-layers with equal thickness and then replaced with n vortex sheets,as shown in Fig.4.According to the relation of continuity of flow and the nonslip condition on the solid surface,the circulation Γiof vortex sheet i is

where L is the characteristic length of the surface panel.The distance yi0of vortex sheet i from the solid surface can be determined as:

where s stands for the number of numerical solution between hiand hi+1.
3.2 Replacement with vortex particles
To simplify the evaluation of interaction between vortex sheets and particles,all the vortex sheets are replaced by equivalent discrete spherical vortex particles,with a Gaussian distribution of vorticity around their centers.
As an example,a triangular vortex sheet is used to illustrate the computation as shown in Fig.5.The vortex sheet is replaced by three particles with equal strength α1=α2=α3=γi·Si/3.And their positions are given by:

Fig.5 Replacement with vortex particles

Further,all the particles on the same vortex sheet i are forced to have equal normal convective velocity vi0across the shear layer,which can be obtained based on the solution of Blasius'equation[20].

3.3 PSE method versus the present method
We will now test the new scheme on 2D vortex panels with uniform strength Δγ and length l,located on the x axis and diffused toward the positive y direction,as shown in Fig.6.The computational grid is established with dx=dy=0.01.The parameters of the simulation are:l=0.01,Δγ=0.4,Δt=0.05 and ν=0.002.
Given Δγ,ν and l,we can figure out the thickness of laminar boundary layer h=0.05.Then the boundary layer is divided into five sub-layers and replaced with equivalent vortex sheets.The computed results of strength,position and normal velocity for each vortex sheet are shown in Tab.1.The sum of circulation is about 3.97×10-3,very close to the exact solution of 4.0×10-3.

Fig.6 Vortex panels,vortex sheets and vortex particles

Tab.1 Computed results of vortex sheets
In the PSE method,the particle i located at(xi, yi)receives,from the vortex panel j,an amount of circulation given by[21]:
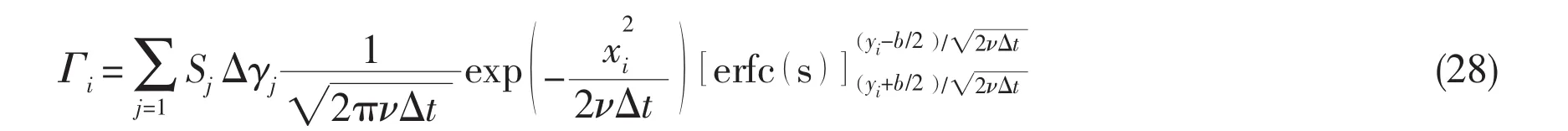
As the number of vortex panels j=1,3,5 and 7,the computed results are provided in Tab.2.As shown by the data,the sum of received circulation is consistent with the previous result,when j is greater than 5.
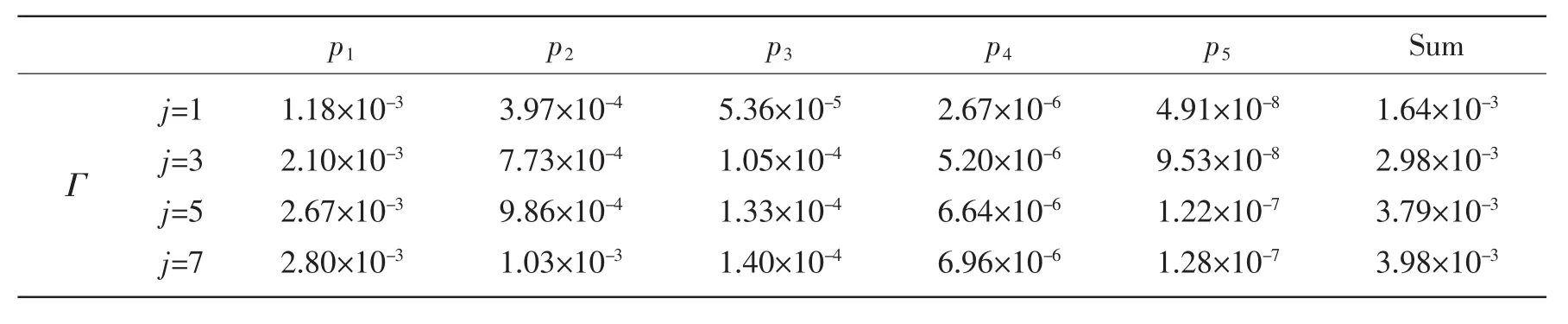
Tab.2 Computed results of vortex particles
In conclusion,the two methods simulate the diffusion process by creating vortex particles in different ways.Comparing with the mathematically deduced method(PSE),the new one avoids solving a large-scale system of linear equations and has an explicit physical meaning.Besides,the proposed scheme has better convergence characteristics even for the irregular grid.Thus,a non-uniform meshing technique can be adopted to adaptive complex solid surface.It can not be denied that,due to ignoring of influence between nascent vortex particles,vorticity distribution around the boundary surface is not as‘smooth'as in the PSE methods.
4 Application examples
Simulations for an impulsively started sphere are performed to validate the present method,for these flows has been extensively studied[9,22-25].
4.1 Re=300
We first computed the flow at a Reynolds number Re=U∞D/v=300,with U∞along the positive x direction.The sphere surface was discretized into 1 180 triangular elements.And the covering vorticity layer was divided into five sub-layers for simulating the diffusion process.The time step was set as ΔT=ΔtU∞/D=0.005.To keep particles core overlap,redistribution was performed every five steps.The computation was completed at T=tU∞/D=75 as the number of particles reached about 365 000.
As shown in Fig.7,a vortex ring adjacent to the rear surface of the sphere is formed at time T=3.Being convected,the axisymmetric vortex ring gradually becomes a non-axisymmetric,double-thread wake extended to the downstream.The hairpin vortex generated at time T=8 and the complete extent of wake at the end of simulation(T=75)are also provided in the figure.And the simulated wake of vortex structure is subject to the same trend as the experimental study conducted by Johnson[25].
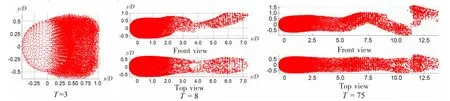
Fig.7 Instantaneous flow pattern represented by vortex particles at Re=300

Fig.8 Time history of fluid force coefficients at Re=300
Fig.8 shows the comparisons between measured and calculated force coefficients CDand CLversus time.The force acting on the sphere oscillates with the change of wake structure and gradually becomes clearly periodic.And the force coefficients are roughly consistent with previous numerical solutions and experimental investigation.
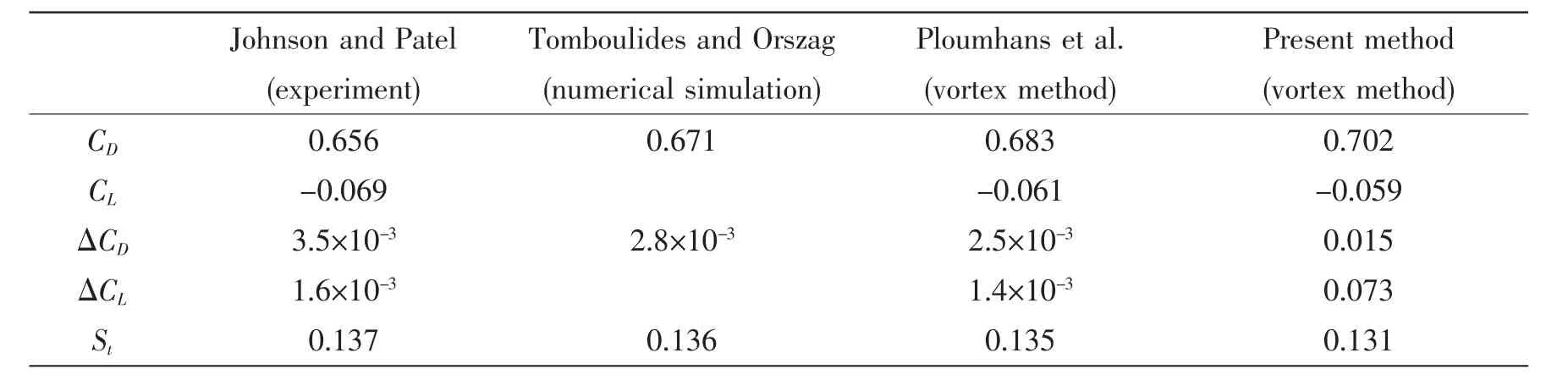
Tab.3 Comparison of force coefficients and Strouhal number with previous results
The computed average values of CDand CLare 0.702 and-0.069,with respective oscillation amplitudes of 1.53×10-2and 7.26×10-2,and the Strouhal number is St=fD/U∞=0.131.Comparing with the experimental data,the mean values of CD,CLand Stare calculated with a reasonable level of accuracy,but ΔCDand ΔCLare significantly overestimated.Because the hydrodynamic force excitation from the turbulent flow is computed by evaluating large numbers of particle interactions,which results in the incorrect high frequency components.Obviously,the simulation of Ploumhans et al can achieve a high accuracy,and Tomboulides et al gave a more accurate result,but our method can substantially improve the computing efficiency.
4.2 Re=500
The flow at Re=500 was also calculated with the same computational grid on the sphere surface as the former case.Most of the simulation parameters were identical to those used in Section 4.1 except the thickness of vorticity layer.The simulation was completed at T=70,with the number of particles remained within the computational domain up to about 759 500.

Fig.9 Instantaneous flow pattern represented by vortex particles at Re=500
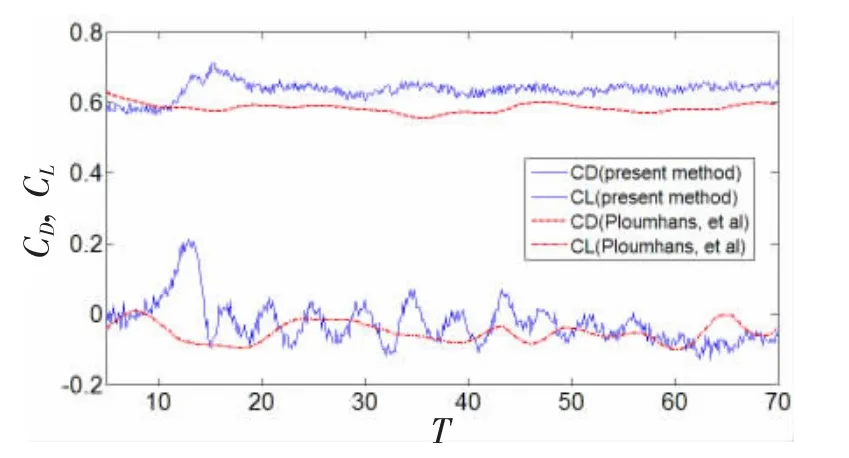
Fig.10 Time history of fluid force coefficients at Re=500
The time histories of drag and lift coefficients are provided in Fig.10.Clearly,they do not become periodic.The achieved CLmatches very well with the calculated lift coefficient in Ref.[9],but the CDis slightly higher than that obtained by Ploumhans et al.
5 Conclusions
An efficient vortex method with a new scheme for vortex sheet diffusion,accelerated by the adaptive fast multipole method,was proposed and applied to the computation of unsteady flows around a sphere.The following conclusions can be obtained:
(1)The adaptive fast multipole method is used to calculate the velocity and its gradient from the vorticity in O (N p3/2)operations,computational efficiency is greatly improved.
(2)The new diffusion scheme is used in three sub-steps:(i)vorticity layer computation(ii)equivalent to discrete vortex sheets and(iii)replaced with nascent vortex particles.
(3)The flows past a sphere are computed at Reynolds number Re=300 and 500 using the proposed method.And a reasonable agreement between our results and that from previous experimental and numerical work is obtained.
It is found that the method developed in the present study is very efficient and convenient for the investigation of bluff body-fluid interactions.For the sake of low discretization resolution and discontinuity of vorticity distribution,our results have slightly lower accuracy in contrast to other simulations.
杂志排行
船舶力学的其它文章
- Time Domain Analysis on Ship Motions in Waves with Translating-Pulsating Source Green Function
- A Multiple Validation Based Methodology of Confidence Level Assessment for Virtual Test of Ship Hydrodynamics
- Research on the Mechanism and Characteristic of Added Resistance of Moonpool with Recess
- LQR Control of a Three Dimensional Underwater Glider
- Research on the Design and Parameter Influence Law of A High-Static-Low-Dynamic Stiffness Vibration Isolator Using for Marine Equipment
- Experimental Investigation on Dynamic Behavior of Porous Material Sandwich Plates for Lightweight Ship
