LED可见光通信系统中应用基于密度的聚类算法的信号判诀
2019-07-08于伟翔胡昉辰卢星宇
于伟翔,石 蒙,胡昉辰,卢星宇,迟 楠
(复旦大学通信科学与工程系,上海 200433)
引言
基于发光二极管(light-emmiting diode, LED)的可见光通信(visible light communication, VLC)由于与传统无线通信相比具有更高的传输速率、更低的使用成本和无需授权的特点,得到了广泛关注[1-4]。但是,基于LED的高速VLC系统仍然受到LED带宽有限问题的限制。所以,我们广泛使用诸如脉冲幅度调制[5]、正交频分复用[6]、无载波幅度相位[7](carrierless amplitude/phase, CAP)等高阶调制以实现更高速率的传输。其中CAP调制是由贝尔实验室在正交幅度调制(quadrature amplitude modulation, QAM)基础上提出的一种重要调制方式,和QAM的区别在于CAP不需要载波源[8]。在VLC系统中,CAP调制已经被证明了适合这种带限系统,并且和QAM和OFDM相比,凭借其结构简单、计算复杂度低的优势更适合短距离通信[9]。但是在实际应用时,系统常受到外部光干扰、功率波动等噪声和非线性的影响。这些影响不仅会降低系统的信噪比,还会产生幅度抖动[10]。前向纠错(forward error correction, FEC)适用于纠正统计意义上分布均匀的噪声产生的错误,而对于由于幅度抖动产生的密集错判信号效果甚微。
机器学习作为一种自适应技术,为我们解决非线性问题提供了强有力的帮助。2017年我们提出并证实了用K-means聚类方法均衡CAP系统中的非线性问题[11],但是它是一种基于几何中心的聚类,如果电平受到外部干扰产生大幅度偏移,甚至从原来的二维观察星座图时两个簇有相互重叠的地方,那么K-means也无法将其区分开。为此,我们将CAP中传统的同向-正交二维空间结合接收信号序列,引入数据间的时间关联性,拓展为同向-正交-时间的三维空间,并利用同一类信号密度上的紧密关联采用结合机器学习的基于空间密度的群以噪声发现聚类算法(density-based spatial clustering of applications with noise,DBSCAN)进行后均衡后再进行信号判决。
1 研究内容
DBSCAN是一种基于密度的聚类算法,主要有两个参数需要设置:半径E和最小点数MinPts。我们通过设置这两个参数间接设置我们期望的数据密度,即我们把一个点的E邻域内的点数(包括自身)不小于MinPts的数据聚为一类并依次向外延托,然后从另一个新的数据点开始找到新的一类,直到将所有数据完全遍历。其中不属于任何一类的点被定义为噪声点,如图1所示。
将图1(a)中的9个点用DBSCAN进行聚类,设置MinPts=3。假设从点A1开始,A1的E邻域中包括自身共有三个点,标为一类,且A1为核心点,接着按顺序遍历A2、A3的邻域,也都满足密度要求,同样归为一类。重复上述步骤,发现A6、A7的邻域不满足密度要求,标为B1、B2,为非核心点。剩下的N1、N2两点的邻域不满足密度要求,同时也不在任何其他核心点的邻域内,所以归为噪声点。总结一下,图1中点Ai(i=1,2,…,7)的E邻域内的点数不少于3个,定义为核心点,而点Bi(i=1,2)本身不满足密度要求,但是从属于核心点的E内,被定义为非核心点,也被聚为和点Ai的一类。而点Ni(i=1,2)本身不满足密度要求,也不属于某一个核心点的E邻域,所以被判为噪声点。

图1 MinPts=3时的聚类原理及效果图Fig.1 Classification when MinPts=3
如图2所示,当半径E取值过小或MinPts取值过大即对密度要求较大时,会出现图2(a)所示的样子,本该聚为一类的数据点被分成很多段,同时被判为噪声的数据点占比较大。相反,当半径E取值过大或MinPts取值过小即对密度要求较小时,会出现图2(b)所示的情况,本该被区分开的两类被错误地聚为一类。
图3(a)所示为当产生振幅抖动时,由于是对每个点单独判决,采用欧式距离的传统硬判决会将超过判决门限(图3(a)中实线a)的点全部判错。而利用图3(a)两个圈中密度的不同,使用DBSCAN将上下两个幅度的点分为两类,对每一类点求平均值(图3(b)中虚线b、c),此时发现两类点的均值未超过判决门限,从而纠正了在抖动峰值处本来会被误判的数据,降低了误码率,提升系统性能。

图2 不同情况时的聚类效果Fig.2 Classification at various requirements

图3 面对振幅抖动采用传统硬判决和DBSCAN时的结果Fig.3 Traditional and DBSCAN-based signal decision meeting with amplitude jitter
2 实验及结果
2.1 实验平台搭建
图4是应用DBSCAN后均衡的CAP-4可见光系统框图。在发送端,由Matlab生成的原始随机比特序列经过QAM-4映射,I/Q两路分离,4倍上采样,再通过一对正交的CAP成型滤波器fI(t)和fQ(t)进行卷积运算后相加,接着通过任意波形发生器(AWG, Tektronix AWG710)将数字信号转为模拟电信号,经过预均衡板(Eq.)、电放大器(EA)、直流偏置树(Bias Tee),对LED灯(Engine LZ4-20MA00)的红色芯片进行调制,使得LED灯能够在照明的同时通过高速闪烁传输信息。信道上放置了透镜和光栅以控制光的强度。在接收端,使用一个商用PIN光电二极管(Hamamatsu 10784)来检测光信号。然后,接收到的信号由EA放大,并由采样速率为2 Gsamples/s的数字存储示波器(OSC,Agilent 54855A)进行采集记录保存,以便进一步进行离线信号处理。在离线信号处理的过程中,首先对接受信号进行同步和下采样操作,然后通过一对匹配滤波器mI(t)和mQ(t)实现同相和正交分量信号的分离。接着利用一般接收处理采用的CMA均衡算法和本实验创新的DBSCAN算法,最后进行QAM解码并恢复为二进制数据,与原始发送数据进行比对,计算出误码率。
由于传输数据分为I、Q两路进行二维传输,因此为了研究抖动幅度对系统的影响以及应用DBSCAN算法后的提升效果。本文在发射端分别在I、Q路上各自加上外部抖动噪声源以模拟振幅抖动的信道环境,并且通过这种方式可以手动调整抖动的幅度以便在抖动幅度较大甚至严重恶化信道环境的情况下研究DBSCAN算法对于系统性能提升大小的作用。
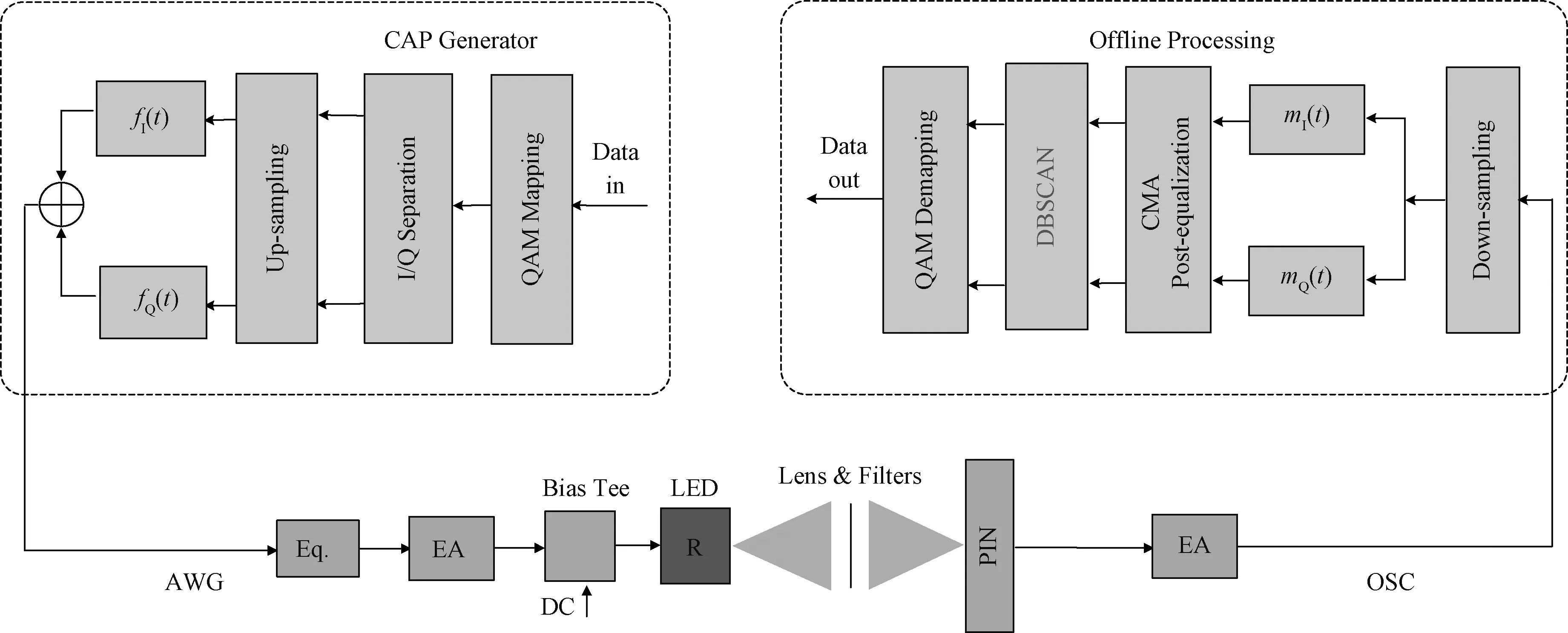
图4 可见光实验系统框图Fig.4 Block diagram of VLC experiment system
2.2 实验结果分析
我们在I、Q两路分别先后加上的抖动波形如图5所示。我们首先对I路进行实验,测量其最佳工作点,即选取合适的驱动电压(VPP)和直流偏置电压(DC)使得LED灯工作在最佳电压区间,结果如图6所示。
当直流偏置为2.0 V,电流为63 mA时,从图6(a)中可以看出,最佳驱动电压为0.3 V。VPP小于0.3 V时,信噪比不够,误码率(BER)增大;VPP大于0.3 V时,非线性增强,误码率增大。当VPP=0.3 V时,从图6(b)中可以看出,最佳直流偏置为2.0 V。DC小于2.0 V时,信噪比不够,误码率增大;DC大于2.0 V时,接收端PIN饱和,系统无法正常工作,所以并未在图中展示。
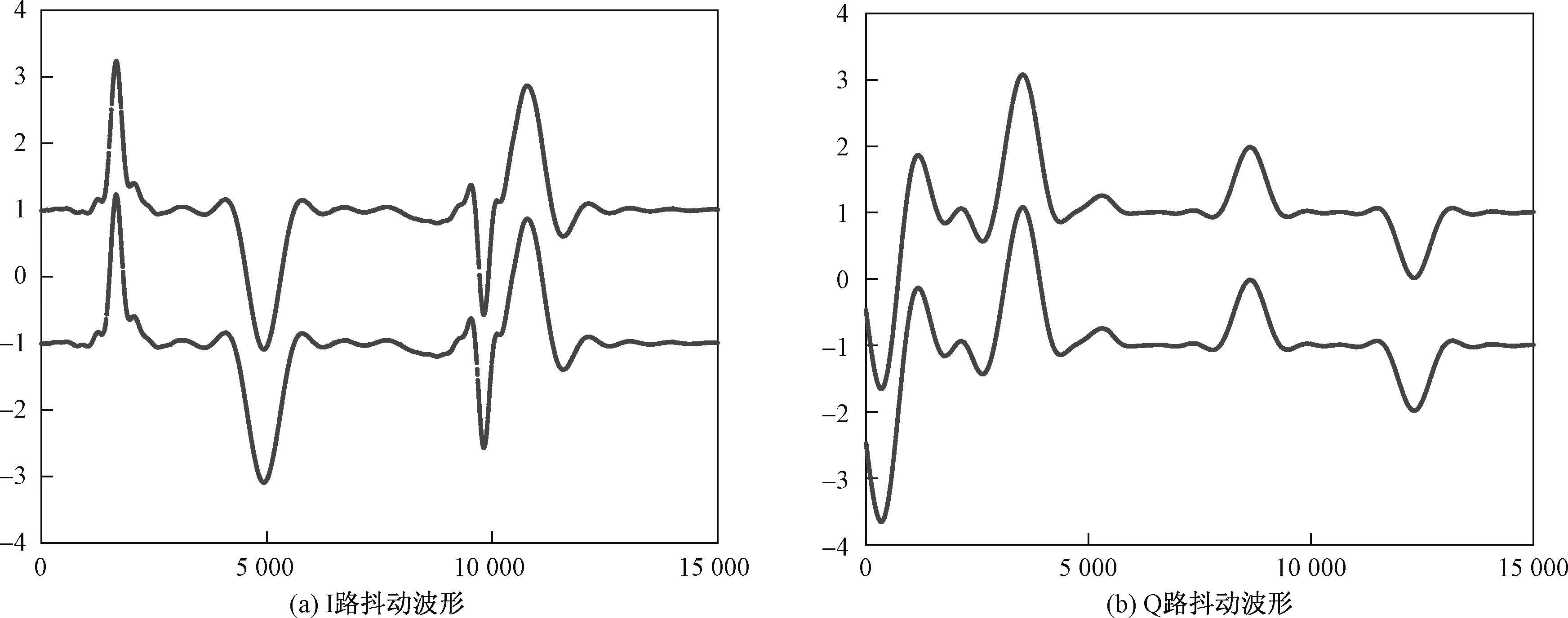
图5 抖动波形Fig.5 Jitter waveform

图6 有无DBSCAN时BER与VPP、DC的关系Fig.6 BER of with and without DBSCAN versus VPP and DC
在最佳工作点VPP=0.3 V、DC=2.0 V的条件下使用DBSCAN的效果如图7所示。图7(a)为使用CMA均衡并经过相位旋转后得到的星座图。图7(b)为根据图7(a)用欧氏距离判决所得结果的误码情况,叉(X)为被误判的星座点。可以看到,抖动处超过所在象限的部分全部被错判。因为QAM4标准星座点只有四个,各在一个象限,所以传统判决就是判断每个点分别在第几象限。图7(c)为使用DBSCAN算法后得到的聚类星座图,一共四类,对应CAP4的四个标准星座点。图7(d)为根据左图进行判决所得结果的误码情况,可以看到,抖动尖峰处的星座点绝大部分都判决正确。
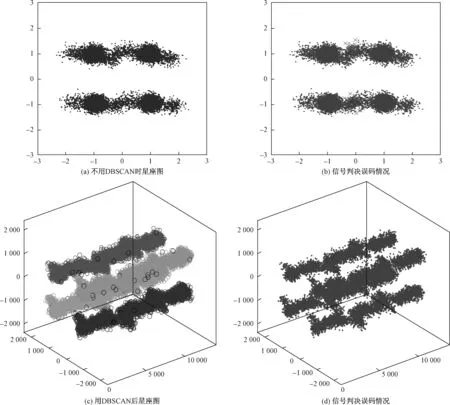
图7 有无DBSCAN时信号判决星座图Fig.7 Signal decision comparison of with and without DBSCAN
图8为I路抖动下系统BER与发送带宽的关系。由图中可以看出,随着发送带宽的增大,误码率也在随之不断增大,带宽大于200 MHz时,使用CMA后均衡算法之后误码率也依旧大于误码门限0.003 8。而使用DBSCAN之后,在本次实验200~375 MHz带宽范围内,均能使误码率低于门限值0.003 8。

图8 有无DBSCAN时BER-Bandwidth关系图Fig.8 BER comparison of with and without DBSCAN in system of different bandwidth
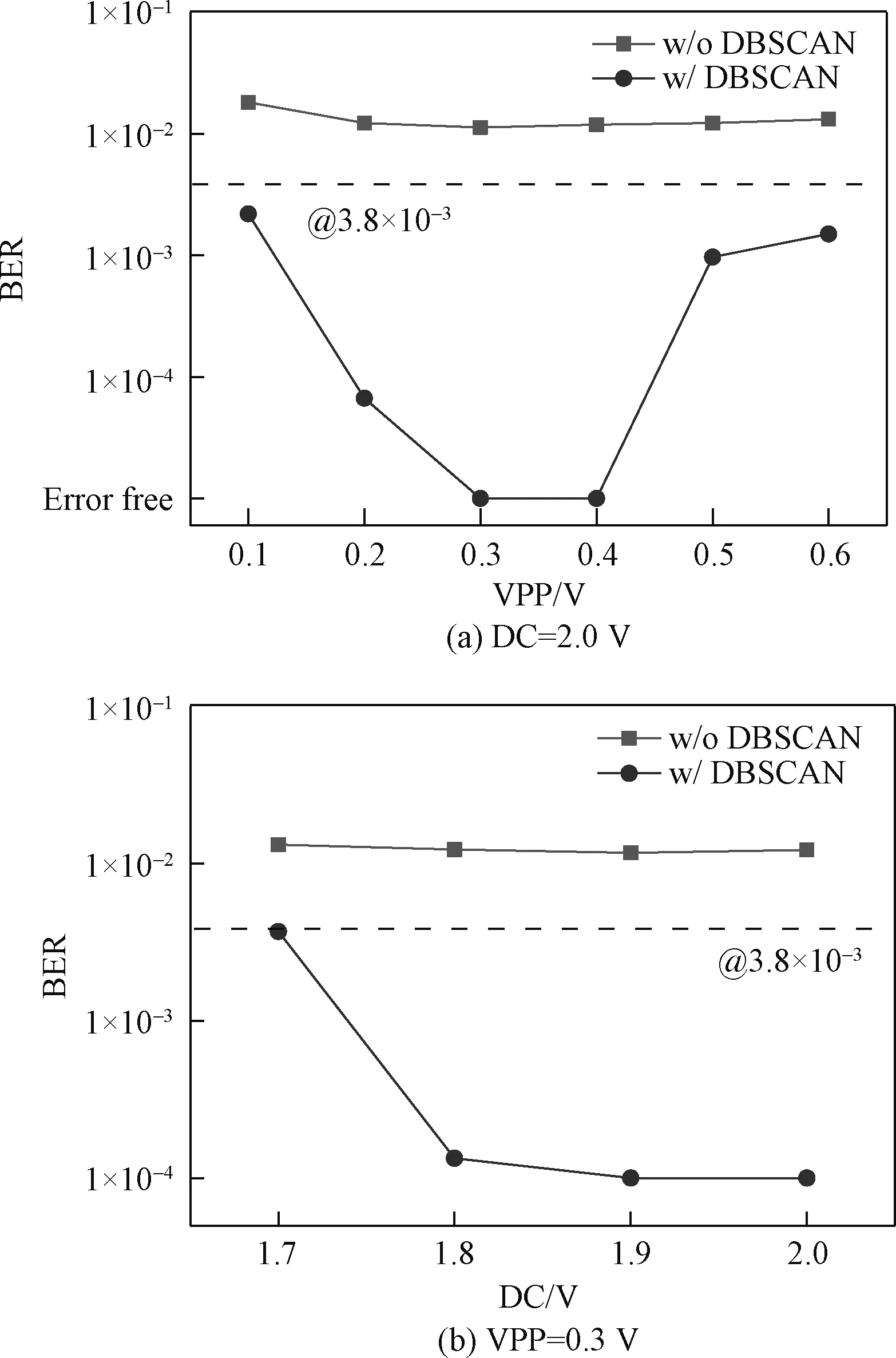
图9 有无DBSCAN时BER与VPP、DC的关系Fig.9 BER of with and without DBSCAN versus VPP and DC
接着对Q路进行实验,同样,先测量最佳工作点,如图9所示。当直流偏置为2.0 V,电流为63 mA时,从图8 (a)中可以看出,最佳驱动电压为0.3 V。VPP小于0.3 V时,信噪比不够,误码率增大;VPP大于0.3 V时,非线性增强,误码率增大。当VPP=0.3 V时,从图9(b)中可以看出,最佳直流偏置为1.9 V。DC小于1.9 V时,信噪比不够,误码率增大;DC大于1.9 V时,系统非线性增强,误码率增大。
在最佳工作点VPP=0.3 V,DC=1.9 V的条件下使用DBSCAN的效果如图10所示。可以看出,DBSCAN的效果和在I路上应用时相似,极大地纠正了原本在抖动尖峰处而被误判的大部分星座点,效果显著。
图11为Q路抖动下系统BER与发送带宽的关系。可以看出,随着发送带宽的增大,误码率随之不断增大,带宽大于250 MHz时,使用CMA后均衡算法之后误码率依旧大于误码门限0.003 8。而使用DBSCAN之后,在本次实验200~425 MHz带宽范围内,均能使误码率低于门限值0.003 8。
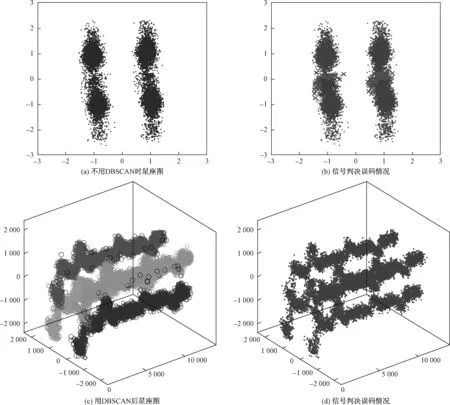
图10 有无DBSCAN时信号判决星座图Fig.10 Signal decision comparison of with and without DBSCAN

图11 有无DBSCAN时BER-Bandwidth关系图Fig.11 BER comparison of with and without DBSCAN in system of different bandwidth
为了进一步比较DBSCAN算法和传统硬判决的性能在不同情况下的提升情况,我们还调整了不同的抖动幅度以进一步研究DBSCAN算法的优势。图12(a)和(b)分别为调整I路和Q路上抖动幅度时DBSCAN算法对系统误码率的减小情况。抖动幅度的单位以CAP4相邻两标准星座点间幅度差为单位1。可以看出,无论是I路还是Q路,抖动幅度小于0.4时,用不用DBSCAN算法系统误码率都为0;抖动幅度大于0.5时,不用DBSCAN算法的开始出现误码;在抖动幅度大于0.75时,不使用DBSCAN的系统误码开始超过误码门限0.003 8;而抖动幅度小于1.3时,使用DBSCAN可以保持系统误码在门限0.003 8以下,说明使用DBSCAN算法后再对星座点进行判决对于系统性能的提升有很大帮助。在所测数据中未使用DBSCAN算法时误码率超过0.003 8门限的情况下,在抖动幅度分别为0.98和1.2时,DBSCAN算法对系统性能提升最大,分别高达4.77 dB和4.43 dB。

图12 有无DBSCAN时误码率与抖动幅度关系图Fig.12 BER comparison of with and without DBSCAN in system of different jitter amplitude
3 总结
我们提出并用实验验证了一种结合机器学习的基于密度聚类算法的信号判决方法,以处理可见光CAP系统中振幅抖动较大情况下传统判决方法效果差、误码率高的问题。我们还研究了DBSCAN算法在遇到不同抖动幅度时对系统性能提升的影响程度。当抖动幅度大于0.5时,传统信号判决方法性能迅速恶化,但应用DBSCAN算法之后;在抖动幅度小于1.2时,系统BER始终保持在误码门限值0.003 8之下。系统性能在I、Q路抖动时最大提升分别为4.77 dB和4.43 dB。这是结合机器学习的DBSCAN算法的信号判决方法在CAP-4系统中的创新应用,新的信号判决方法对系统性能的提升效果显著。
