例谈一个不等式的应用

安徽省枞阳县第三中学 (246700)

胡周霞

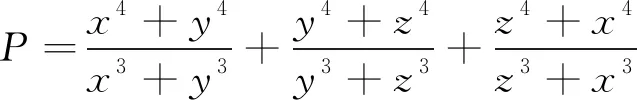
这是2018年第1期《数学通讯》(上半月)问题征解的第331题，试题小巧轻灵，结构均匀优美，看到问题中分式结构中的高次幂，首先想到的是降幂处理.

由证明的过程，我们可以看到解决问题的本质是不等式：x4+y4≥x3y+xy3的运用，而这个不等式是来自高中数学教材选修4—5的一个例题.进一步，可以得到：

设x,y>0且有m∈N*,l∈N*,m≥l,则有xm+ym≥xm-lyl+xlym-l.

本文主要谈谈该不等式在解题中的应用.有了这个不等式，我们首先得到问题331的几个推论，证明过程留给读者.

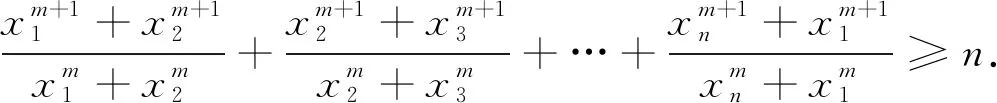
证明：∵a5+b5≥a3b2+a2b3=a2b2(a+b),

下面式子的证明和例3的证明方法完全相同，读者不妨尝试一下.

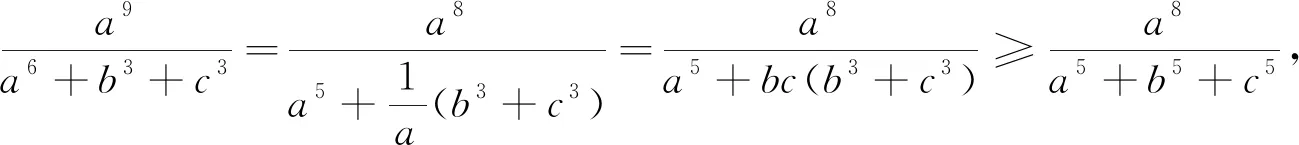
例4的一个直接推论就是《数学通报》2367号问题.

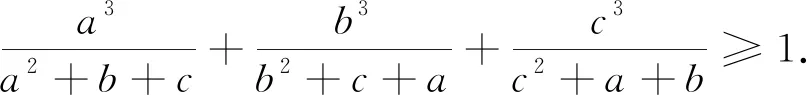
下面两个式子的证明和例4的证明方法完全相同，读者不妨尝试一下.

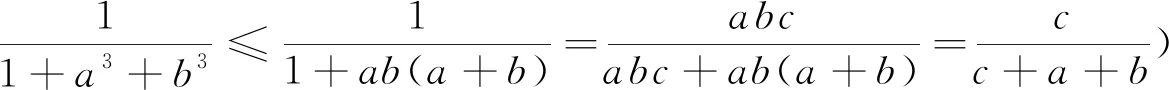
我们看到不等式xm+ym≥xm-lyl+xlym-l看似简单，实则锐利.灵活地加以运用，可以又快又好的解决一些看似高不可攀的数学难题.它的本质就是排序不等式的初级形式，解题中有时也走了一点弯路，比如例4中a8+b8+c8≥abc(a5+b5+c5)的证明用xm+ym≥xm-lyl+xlym-l来证有点繁琐，而在排序不等式中它是一个显然的事实.