几个代数不等式猜想的证明

广东广雅中学 (510160)

杨志明

文[1]提出4个不等式猜想，其中猜想3是：

笔者在文[2]中证明了此猜想,最后提出了与之相关的4个猜想:

文[3]试图采用正切代换给出(1)和(4)的一种证明，可惜，作者犯了一个低级错误．由于(1)和(4)式均是关于a,b,c的轮换对称不等式，所以只能指定a,b,c的最大值或最小值，而不能指定a,b,c的大小顺序．因此，文[3]中的所有结论均未证明成功．

事实上，文[3]除了试图证明(1)和(4)式外，还给出了如下几个结论：

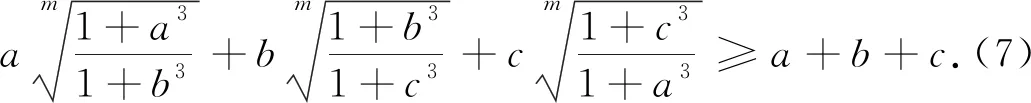
事实上，定理1-3均成立，而且可以统一推广为：

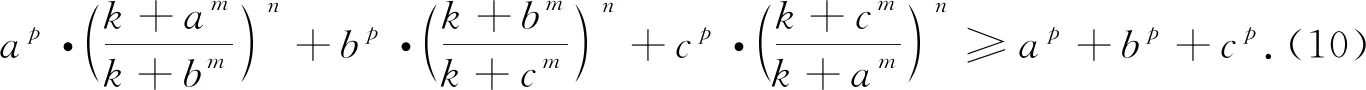
故原不等式等价于ap(x-1)+bp(y-1)+cp(z-1)≥0．

不妨设a=max{a,b,c}，则x≥1．

当a≥b≥c≥0时，ap≥bp≥cp≥0，y≥1,z≤1．

由x+y+z≥3知，z≥3-(x+y)．

ap(x-1)+bp(y-1)+cp(z-1)≥ap(x-1)+bp(y-1)+cp[3-(x+y)-1]=ap(x-1)+bp(y-1)+cp[(1-x)+(1-y)]=(ap-cp)(x-1)+(bp-cp)(y-1)≥0．

当a≥c≥b≥0时，ap≥cp≥bp≥0，y≤1,z≤1．

由x+y+z≥3知，z≥3-(x+y)．

ap(x-1)+bp(y-1)+cp(z-1)≥ap(x-1)+ap(y-1)+ap(z-1)=ap[(x-1)+(y-1)+(z-1)]=ap[(x+y+z)-3]≥0．

综上可知，ap(x-1)+bp(y-1)+cp(z-1)≥0．

故不等式成立．

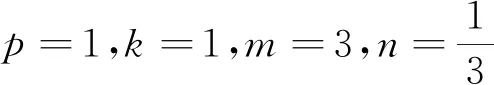
当p=1,k=1,m=1,n=1时，即得定理3．

至此，文[3]中的定理1-3已经全部证明了，剩下定理4没有解决，这留给有兴趣的读者．

事实上，我们还可以给出定理3的另一种推广．

证明：不妨设c=min {a,b,c}，a=c+x,b=c+y(x,y≥0)，则原不等式等价于f(c)=2(k+1)(x2-xy+y2)c2+[(x2-xy+y2)k2+[(x3+y3+2x2y-xy2)+4(x2-xy+y2)]k+(x3+y3+2xy2-x2y)+3(x2-xy+y2)]c+(x2y+x2-xy+y2)k2[(x3y+x3+y3+xy2+2(x2-xy+y2)]k+xy3+(x3+y3+xy2-x2y)+(x2-xy+y2)≥0．

由均值不等式知，x2+y2≥2xy，即x2-xy+y2≥xy≥0，x3+xy2≥2x2y，故x3+xy2-x2y≥x2y≥0，从而x3+y3+2xy2-x2y≥0，因此，关于f(c)的每项系数均为非负，命题得证．

特别地，当k=0，由命题2即得定理3．

需要特别说明的是，对本文中的命题1和2中的各个变量进行赋值，可以生产出成千上万的三元不等式，有兴趣的读者不妨一试．