公式法教学亟待重视元的可变性

江苏省苏州市吴中区苏苑高级中学 (215128)

蒋凤燕 杨品方

对于数学学习，有种普遍说法，就是可以套用公式．也正因为口诀公式定理的重要，所以我们的数学老师在新授课复习课时都热衷于默写公式，针对一些不能准确默写的还要罚抄，可以理解．虽然学生能准确默写公式了，但是在套用公式的时候，还是免不了发生错误或者说是多走了不少的弯路．

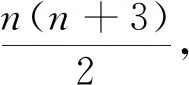
一、重视元的外表形式的可变性

一般地，公式简洁明了，我们要赋予简洁字母以实际意义，还要指出一些常用的变形．

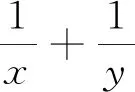
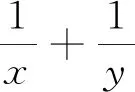
二、重视元的主次地位的可变性

再比如，在区间[0,2π)上，研究关于x的方程mcosx+m2+1=0的解的可能情况．我们可以整理方程为m2+cosx×m+1=0，这是关于m的一元二次方程，Δ=cos2x-4×1<0，方程无解，“没有实数m能使得方程成立”，所以关于x的方程mcosx+m2+1=0也无解．

例2 对于满足0≤p≤4的一切实数p，不等式x2+px>4x+p-3恒成立，求实数x的取值范围．

我们的习惯思维是“x”的不等式，从而整理成x2+(p-4)x-p+3>0，由于题目要求x的取值范围，所以二次函数f(x)=x2+(p-4)x-p+3的定义域待定，从而无法求出该函数的值域，就不方便让该函数值与0比较．已知实数p的取值范围，对于某个变量p的函数，就是“已知定义域可求值域”的问题了．于是，反客为主，视p为变量，视x为常数，就可解了．

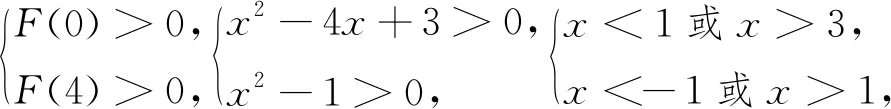
从而x∈(-∞,-1)∪(3,+∞)．

在解题中，需要有一种主元次元地位角色相互转化的意识，而且必须有这种意识，这就好比“三人行必有我师”，要看具体场合的．

三、重视消A元消B元的可变性

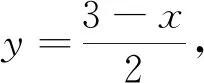
例3 已知数列{an}的前n项和为Sn，满足Sn=2an-1，求数列{an}的通项公式．

学生效仿，当n≥2时，Sn=2(Sn-Sn-1)-1，即Sn=2Sn-1+1，两边同时加1，就有Sn+1=2(Sn-1+1)．由S1=2S1-1解得S1=1，由S1+1=2≠0，Sn-1+1≠0，所以{Sn+1}是首项为2公比为2的等比数列，Sn+1=2×2n-1，Sn=2n-1．故an=Sn-Sn-1=2n-2n-1=2n-1(n≥2)，a1=1满足，所以an=2n-1．

这样的解法有点兜圈子，走远路了．为了求解an的表达式，可以选择消除Sn．

解：取n=1，a1=2a1-1，所以a1=1．当n≥2时，Sn-1=2an-1-1，两式相减，an=Sn-Sn-1=2an-2an-1，即an=2an-1，由于a1=1≠0，所以{an}就是以1为首项、2为公比的等比数列，于是an=2n-1．

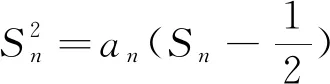
我们知道，由an可以求Sn，反之由Sn也可以求an，那么例3问题能否修改成：“已知数列{an}的前n项和为Sn，满足Sn=2an-1，求Sn的解析式”呢？不合适！这是有意在误导学生对问题的分析！退一步讲，至少也要先求通项再求和，于是“已知数列{an}的前n项和为Sn，满足Sn=2an-1，求数列{an}的通项公式，并求出Sn的解析式．”这就要求我们的老师在编拟试题的时候，不能有意“卡”学生，要注重通性通法问题．

在教学中，我们需要公式，需要活化公式，而不能仅仅停留在公式所用的字母上．