复合高斯杂波下抑制失配信号的自适应检测器

许述文 石星宇 水鹏朗

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)(西安电子科技大学信息感知技术协同创新中心 西安 710071)

1 引言

海杂波背景下的自适应雷达目标检测问题一直得到雷达界的广泛关注。公开文献提出了很多著名的检测器，例如Kelly[1]的广义似然比检验(Generalized Likelihood Ratio Test, GLRT)，自适应匹配滤波器(Adaptive Matched Filter, AMF)[2]以及Maio[3]提出的Rao检验等。上述检测器都是在均匀高斯杂波背景下设计的，也就是说检测单元与参考单元中的杂波服从0均值复高斯分布且协方差矩阵相同。但实际中，由于各种因素，杂波环境(特别是海杂波)通常不符合均匀杂波假设，一种广泛使用的非均匀模型是部分均匀环境[4]，它认为检测单元与参考单元具有结构相同但存在尺度差异的协方差矩阵。然而，随着雷达分辨率的提高和擦地角的减小，海杂波呈现出严重的拖尾现象，传统的高斯杂波模型不再适用，取而代之的是复合高斯模型[5]，它可以表示为相互独立的慢变纹理分量和快变散斑分量的乘积，其中纹理分量为非负随机变量，散斑分量为复高斯随机向量。文献[6]给出了复合高斯杂波背景下最优检测器的结构，文献[7—10]给出了纹理分量服从不同分布时的最优检测器。此外，文献[11]还提出了一种K分布海杂波下称为-AMF的计算可实现的近最优检测器。

上述检测器是在假设信号没有失配的情况下提出的，未考虑可能存在的失配信号。然而，如旁瓣目标、多径传播、阵列校准误差等因素都可能造成信号失配。因此，对主瓣目标检测性能以及旁瓣目标拒绝能力的折中是必须考虑的问题。实际应用中，期望的检测器应该是鲁棒性强的，例如工作在搜索模式下的监视雷达更希望使用鲁棒性强的检测器；然而工作在跟踪模式下的雷达就需要强选择性的检测器，例如当一架飞机位于主瓣波束外而落在旁瓣波束时，为了目标定位的准确性，通常希望拒绝检测该旁瓣目标，直到其进入主瓣波束才应触发一次有效检测。具有选择性的检测器是指当信号发生失配时，其检测概率急剧下降。也就是说具有选择性的检测器不会把大信杂比的失配信号作为感兴趣的信号检测出来。目前公开报道的文献中已经提出了很多选择性检测器，例如均匀环境中的自适应波束形成正交拒绝检验(Adaptive Beamformer Orthogonal Rejection Test, ABORT)[12]、白化ABORT[13]，非均匀环境中的广义白化(Generalized Whitened, GW)-ABOTR-部分均匀环境(Partially Homogeneous Environment, PHE)以及可调(Tunable,T)-GLRT-PHE[14]。

上面提到的选择性检测器仅适用于均匀或非均匀的高斯杂波环境。目前鲜有文献提出复合高斯海杂波背景下信号失配时的选择性检测器。一种常用的选择性检测器设计方法是通过在0假设下引入虚构的干扰来修正假设检验，该虚构的干扰与参考信号在白化空间中是正交的。当信号发生失配时，修正后的0假设将比原来仅包含海杂波的0假设更加可信，检测器就不会倾向于做出存在目标的判决，从而对失配信号具有一定的选择性。本文首先采用该方法修正二元假设检验，然后基于两步GLRT提出复合高斯杂波背景下的选择性检测器，最后通过仿真实验说明所提检测器对匹配信号的检测性能以及对失配信号的选择性能。此外，还将证明所提检测器对海杂波纹理分量以及协方差矩阵的恒虚警特性。

2 检测问题描述

3 检测器设计

3.1 基于两步GLRT的检测器推导

两步GLRT检测器设计过程的基本原理是：首先假设杂波协方差矩阵已知，根据检测单元数据k,k∈ΩP的联合PDF推导GLRT；然后从参考单元中估计杂波协方差矩阵，将用其估计值代替，得到自适应检测器。

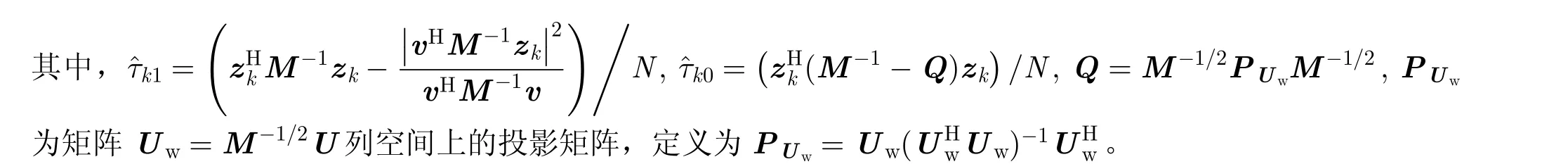
3.2 CFAR性质讨论

4 实验结果

本节通过实验评估所提检测器的检测性能和选择性能，同时还将与已有检测器进行对比。具体来说，参与对比的检测器有GLRT, GAMF, GASD[4]和ABORT，各检测器的具体形式如式(24)—式(27)

SCR的变化曲线。从图中可以看出，对于点目标而言，本文所提检测器对匹配信号的检测性能与GASD相同，但是在高信杂比情况下，相比GLRT以及ABORT检测器有大约1～2 dB的性能损失。由于GAMF检测器是高斯杂波背景下的最优检测器，而实验中使用的是纹理分量服从Gamma分布的复合高斯杂波，因此其检测性能最差。图3给出了各检测器在目标发生距离扩展时的检测性能曲线，这里假设目标占4个距离单元，即H=4。从图中可以看出，当目标被分辨到多个距离单元时，本文所提检测器检测性能明显提升，在不同SCR水平下均优于现有检测器。特别地，在Pd=0.9时，本文所提检测器与GASD相比，有2.5 dB左右的性能提升。

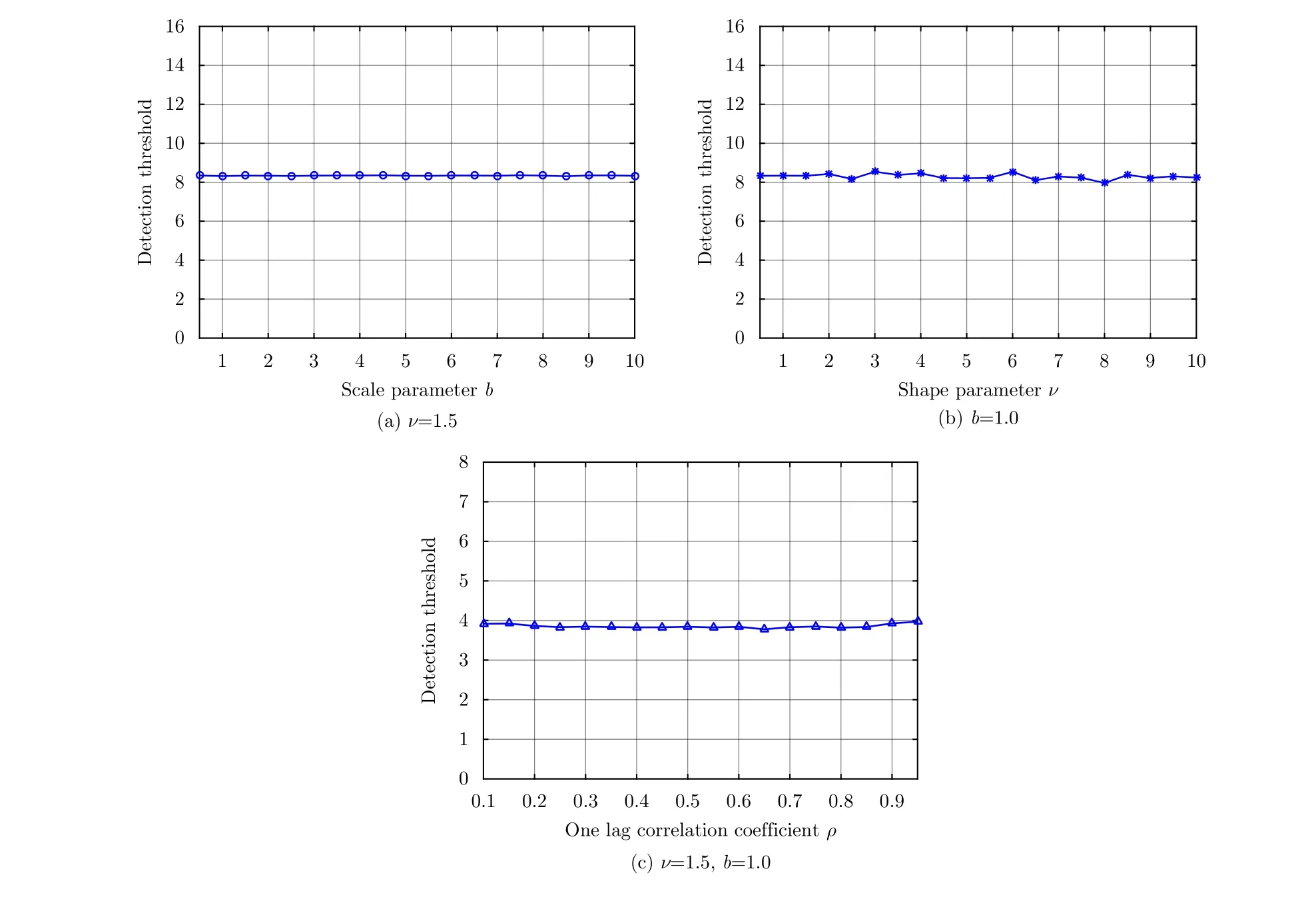
图1 本文所提检测器在不同 ν, b,ρ下的检测门限(H=4, K=32)Fig.1 Detection threshold of the proposed detector under different ν ,b and ρ (H=4, K=32).

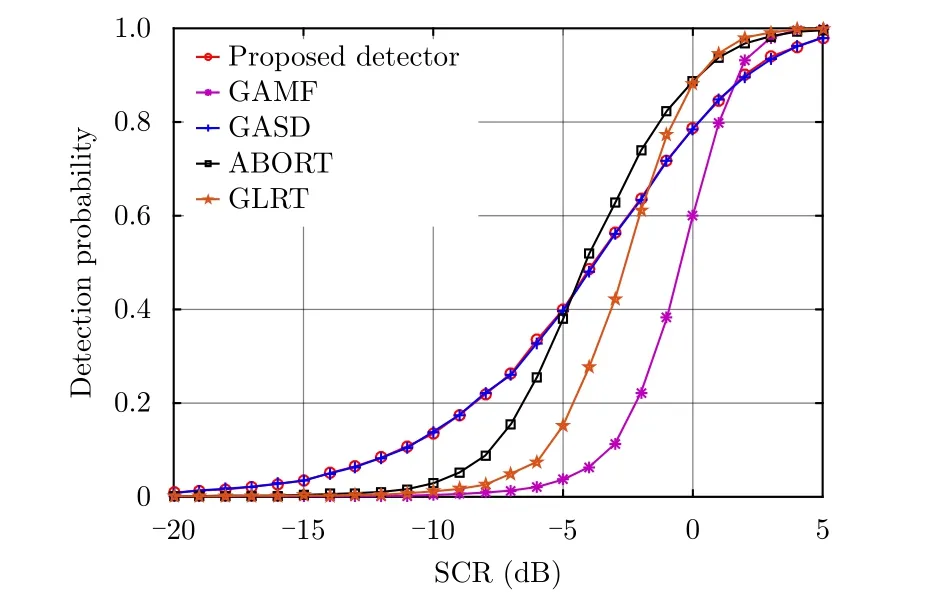
图2 不同检测器对匹配信号的检测性能曲线(N=8, H=1, K=32,cos2θ=1, b=1.0, ν=1.5)Fig.2 Detection performance curve of different detectors for matched signal (N=8, H=1, K=32, c os2θ=1, b=1.0, =1.5)

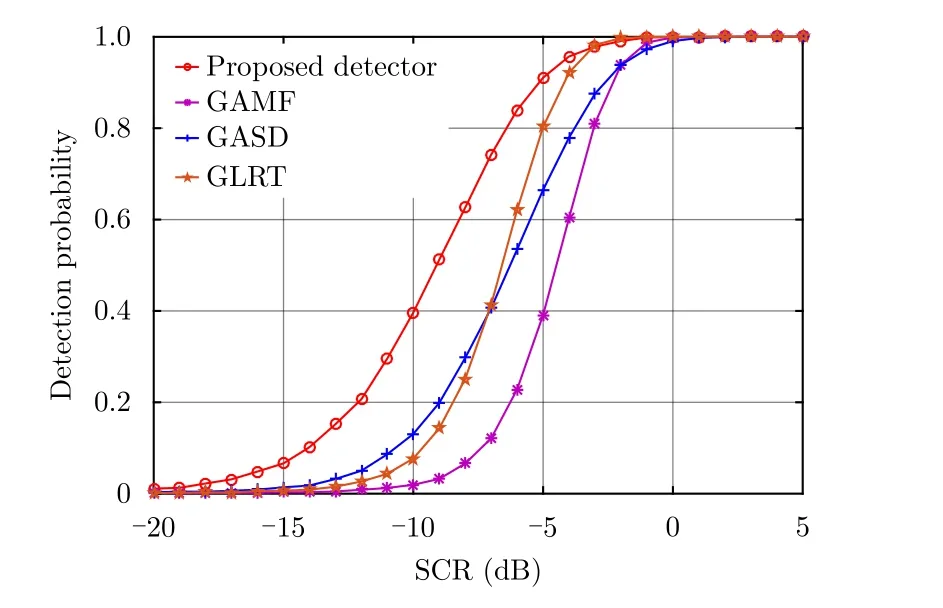
图3 不同检测器对匹配信号的检测性能曲线(N=8, H=4, K=32,cos2θ=1, b=1.0, ν=1.5).Fig.3 Detection performance curve of different detectors for matched signal (N=8, H=4, K=32, c os2θ=1, b=1.0, =1.5)

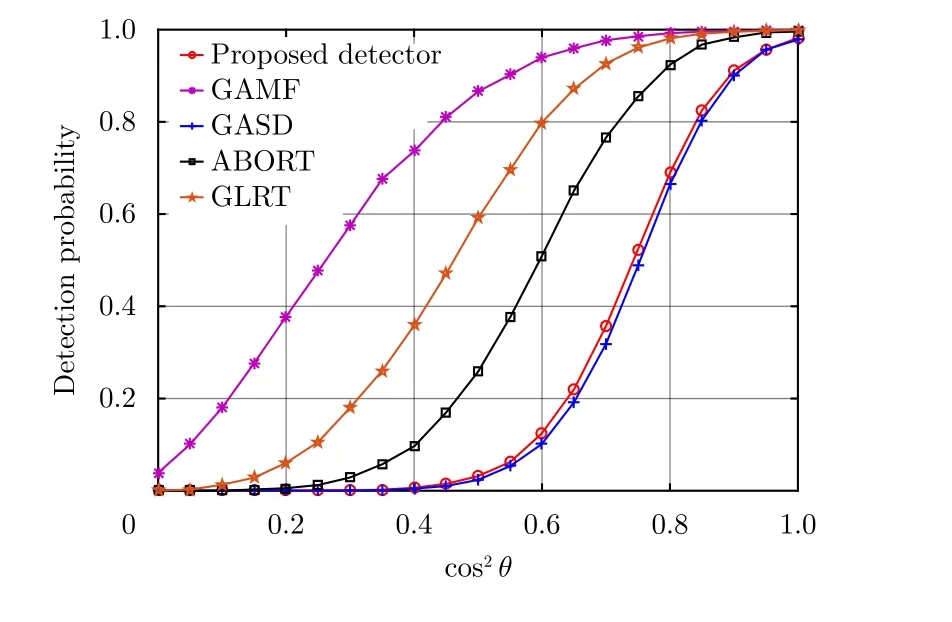
图4 不同检测器检测概率随 co s2θ的变化曲线(N=8, H=1, K=32,SCR=5 dB, b=1.0, ν=1.5)Fig.4 Detection probability of different detectors versuscos2θ(N=8, H=1, K=32, SCR=5 dB, b=1.0, ν=1.5)

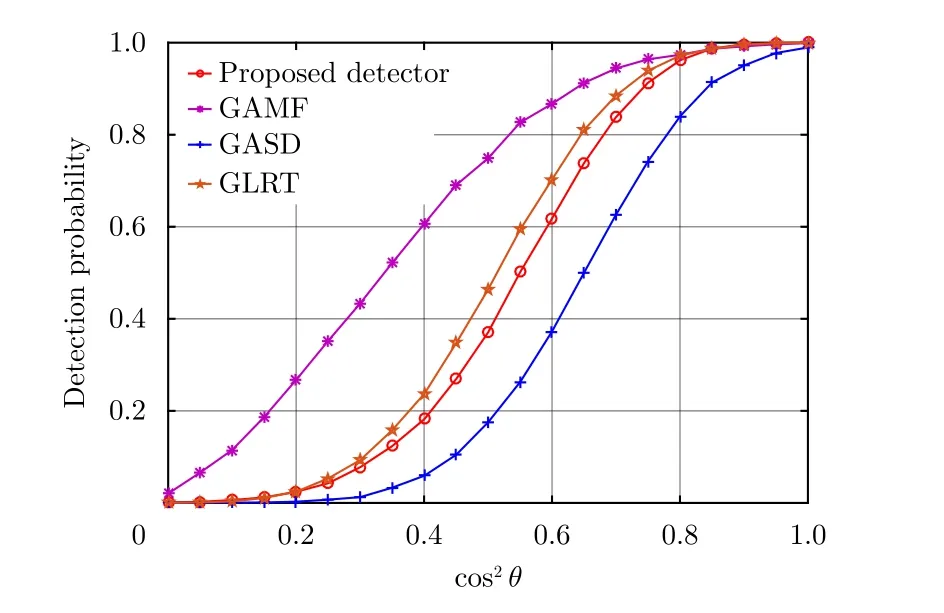
图5 不同检测器检测概率随 co s2θ的变化曲线(N=8, H=4, K=32, SCR=0 dB, b=1.0, ν=1.5)Fig.5 Detection probability of different detectors versuscos2θ(N=8, H=4, K=32, SCR=0 dB, b=1.0, ν=1.5)

下面利用实测数据进一步验证本文所提检测器的性能。采用加拿大McMaster大学X波段高分辨IPIX雷达于1998年在安大略湖采集的海杂波数据进行实测数据分析，文件名为19980204_223753_ANTSTEP，实验雷达工作在4种极化方式(HH,HV, VH, VV)下，数据由28个连续距离单元构成，每个距离单元包含60000个脉冲序列，距离分辨率为60 m。图6给出了瑞利分布以及K分布对该组实测海杂波数据的幅度分布拟合曲线，从图6中可以看出，实测海杂波数据幅度分布具有很重的拖尾，明显偏离瑞利分布，呈现出较强的非高斯特性，高斯背景假设不再成立，而复合高斯杂波模型之一的K分布具有很好的拟合结果。

分别假设实际目标信号与假设的导向矢量匹配或失配，不同情况下的性能曲线如图7及图8所示。由于数据集中仅有28个距离单元，为保证协方差矩阵的有效估计，将实验参数设置为N=8,H=4,K=24。图7显示，在实测海杂波下，相比于传统检测器，本文所提检测器对匹配信号的检测性能在高SCR下有轻微损失而在低SCR下略有提升。在多普勒失配的情况下，由于实测数据协方差矩阵未知，因此图8中保持实际目标导向矢量固定，利用AML得到协方差矩阵的估计值，通过对失配多普勒导向矢量的搜索得到 co s2θ的值。根据图8所示曲线可以发现，本文所提检测器对失配信号的拒绝能力与GASD检测器相当，且选择性好于GLRT及GAMF检测器。

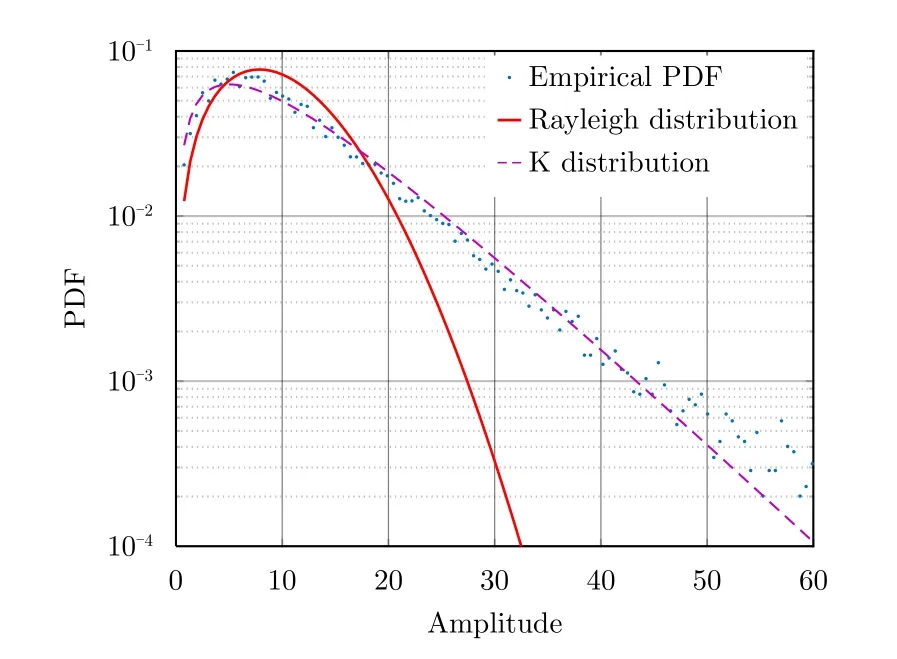
图6 实测数据幅度分布拟合曲线Fig.6 Amplitude probability density function fitting of the measured data

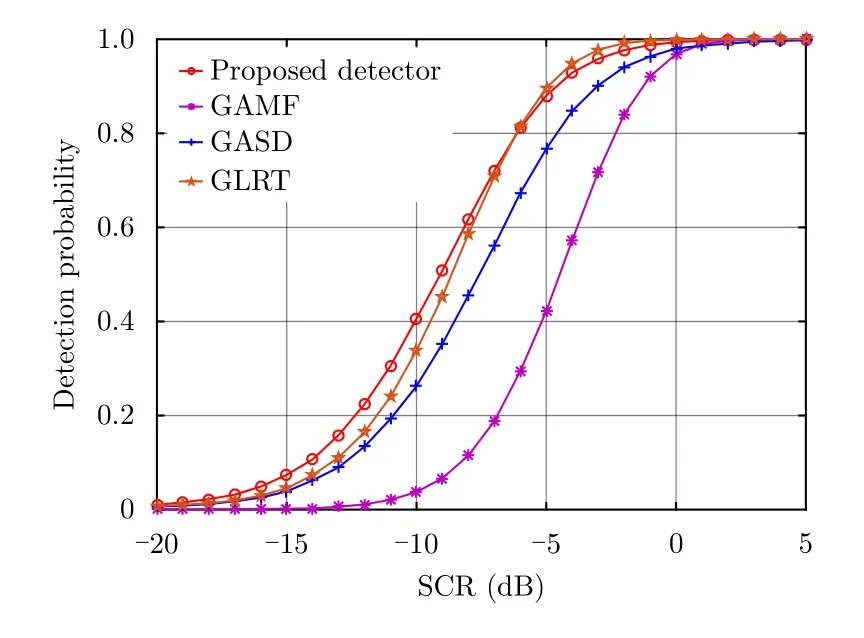
图7 实测数据下不同检测器对匹配信号的检测性能曲线(N=8, H=4, K=24)Fig.7 Detection performance curve of different detectors for matched signal under measured data (N=8, H=4, K=24)

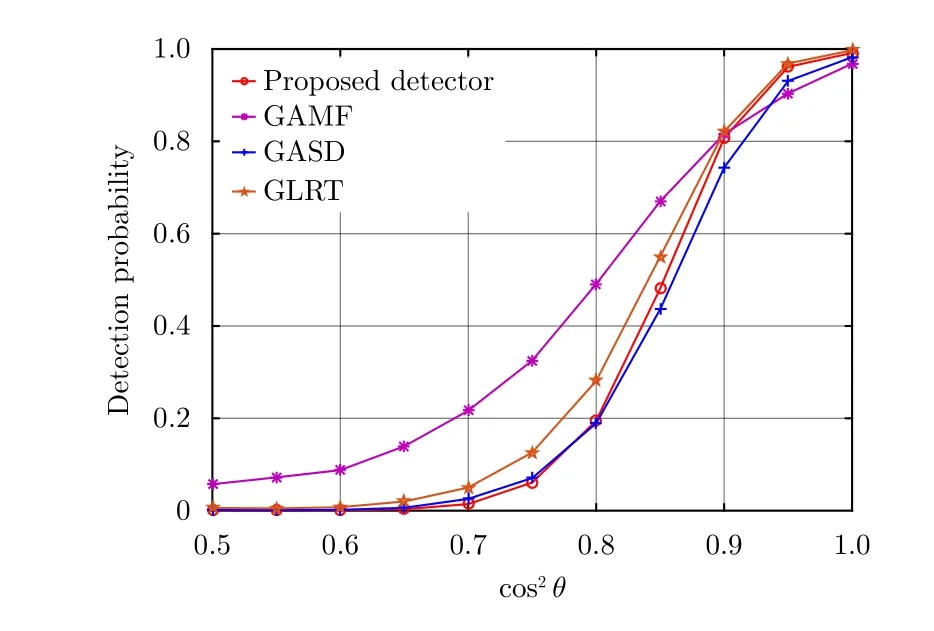
图8 实测数据下不同检测器检测概率随 co s2θ的变化曲线(N=8, H=4, K=24, SCR=0 dB)Fig.8 Detection probability of different detectors versuscos2θ under measured data (N=8, H=4, K=24, SCR=0 dB)

值得注意的是，对海雷达感兴趣的目标往往淹没在种类繁多的海上目标当中，如果对所有目标不加区分地进行检测，势必会造成后端数据处理的压力骤增。而本文所提选择性检测器在几乎不损失匹配信号检测能力的条件下，通过在H0假设下引入虚构干扰信号的方式，使得失配信号在H0假设下的可信度提高，从而有效提高了对多普勒失配信号的拒绝能力，进而减轻数据处理的压力。

5 结论

本文研究了非高斯杂波背景下具有选择性的检测器设计问题。将非高斯杂波建模为复合高斯模型，杂波样本取自球不变随机向量。在纯杂波假设中加入虚构的与目标信号在白化空间正交的干扰信号以修正原始二元假设检验，增加失配信号在0假设下的可信度，达到选择性检测器的设计目的。目标信号及杂波模型中的确定性未知参数用其最大似然估计代替，通过辅助数据估计杂波协方差矩阵，得到自适应的选择性检测器。证明了所提检测器对复合高斯杂波的纹理分量以及协方差矩阵是恒虚警的。此外，蒙特卡洛实验结果还表明，本文所提检测器在点目标情况下性能与GASD相似；在距离扩展目标情况下，对失配信号的选择性较好，且对匹配信号的检测性能有一定改善。