WSNs中基于仿生模型的拥塞控制算法
2019-07-05张莉华
张莉华,曹 斌
(黄淮学院 信息工程学院, 河南 驻马店 463000)
随着短距离通信技术的快速发展,物联网相关技术已成为研究人员关注的焦点。数据采集是物联网应用的关键阶段。微型的、能量受限的具有数据感采集能力的传感节点组成的无线传感网络 (Wireless Sensor Networks,WSNs)[1-2]已在医疗、环境监测、军事等领域得到广泛应用。这些传感节点的主要任务就是感测数据,然后以单跳或多跳方式传输至信宿。
然而,传感节点属微型节点,它对数据处理能力是有限的,节点缓存容量有限。此外,在多数应用环境下,传感节点数是非常多。当这些节点需要传输的数据包数超过缓存容量时,就会导致网络拥塞[3]。而传感节点数越多,网络拥塞越严重。这势必影响网络的服务质量(Quality of Service,QoS),如吞吐量、时延、数据包丢失率。因此,控制网络拥塞成为WSNs的一项关键技术。
文献[4]引用仿生(bio-inspired)拥塞控制策略。通过平衡节点使用资源率或控制节点产生流量的速度,降低网络拥塞概率。然而,该策略并没有强烈节点占用资源的公平性问题,即并非所有传感节点均有相同的机会去传输它的数据包。
为此,提出基于仿生模型的拥塞控制(Bio-inspired based Congestion Control,BICC)算法。BICC算法引用两个仿生算法控制WSNs的拥塞问题。首先,引用竞争洛特卡-伏尔特拉(Competitive Lotka-Volterra,C-LV)模型[5]降低网络拥塞。C-LV模型维持所有节点的公平性,并控制节点产生数据流的速度,进而预防拥塞。引用C-LV仿生算法的目的在于:自适应地控制产生数据流的速度,进而避免网络拥塞。C-LV模型通过合适地选择参数,维持免拥塞地传输流量。然而,选择参数是非常耗时,并且当节点数较多时,选择合适参数是不太可能。
据此,引用第二个仿生算法,粒子群优化(Particle Swarm Optimization,PSO)[6-7]优化C-LV参数。C-LV模型中有一重要的参数必须慎重选择。而PSO算法可以完成这个任务。此外,为了避免拥塞和维持公平,PSO通过优化节点传输率,提高C-LV模型的性能。同时,降低端到端传输时延也是运行PSO算法的目的。
最终,通过引用C-LV和PSO两个算法,BICC算法实现两个目标:控制流量,避免拥塞;最小化端到端时延。
1 BICC算法
BICC算法先利用C-LV优化节点的流量产生率,使各节点能够公平地、无拥塞竞争资源。然后,利用粒子群优化PSO算法优化C-LV模型参数,降低流量的传输时延,算法框图如图1所示。
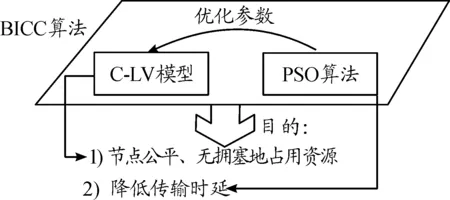
图1 BICC算法框图
1.1 C-LV概述
假定有n个物种,xi(t)表示在时刻t,物种i的群体尺寸(Population Size)。而ri表示在没有其他竞争物种下,物种i的内在增长率。而Ki表示物种i的最大群体尺寸。αij表示物种j的群体对物种i的生长的影响。而αii表示物种i的群体对它自已的生长的影响。
C-LV模型描述了物种竞争资源的关系,如式(1)所示:
∀i∈{1,2,3,…,n}
(1)
物种竞争资源的最终结果不外乎两种:所有物种共同分享资源,达到一种平衡;只有一个物种存在,其他物种灭绝。显然,第一种结果是最优的稳定状态,本文将此称最稳定状态。
1.2 应用于WSNs的C-LV
将C-LV应用于WSNs的流量控制,在不产生网络拥塞的前提下,使各节点均能公平接入网络,接入后再传输数据。即达到C-LV模式第一种结果。
在WSNs中,每个节点需要将自己所感测的数据传输至信宿。而信宿具有有限的缓存区域。当多个节点同时传输感测数据,或者所形成的数据流量超过信宿的缓存区域,则就形成数据丢失。因此,信宿的缓存区域是各数据流所竞争的资源。
图2为系统模型。系统内有n个传感节点,每个节点需要向信宿传输自己的数据流。将C-LV应用于WSNs后,物种、群体尺寸、竞争和资源的对应关系,如图3所示。将传感节点所需传输的流量看成物种,这些物种竞争网络资源。而流量的字节数表示物种的群体尺寸。
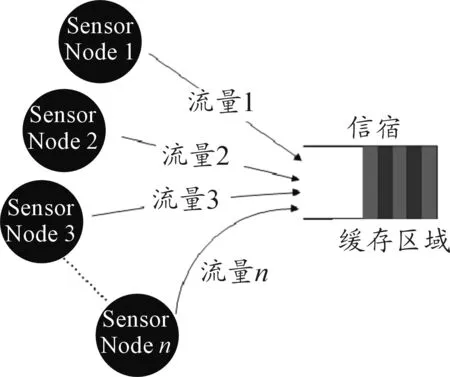
图2 系统模型
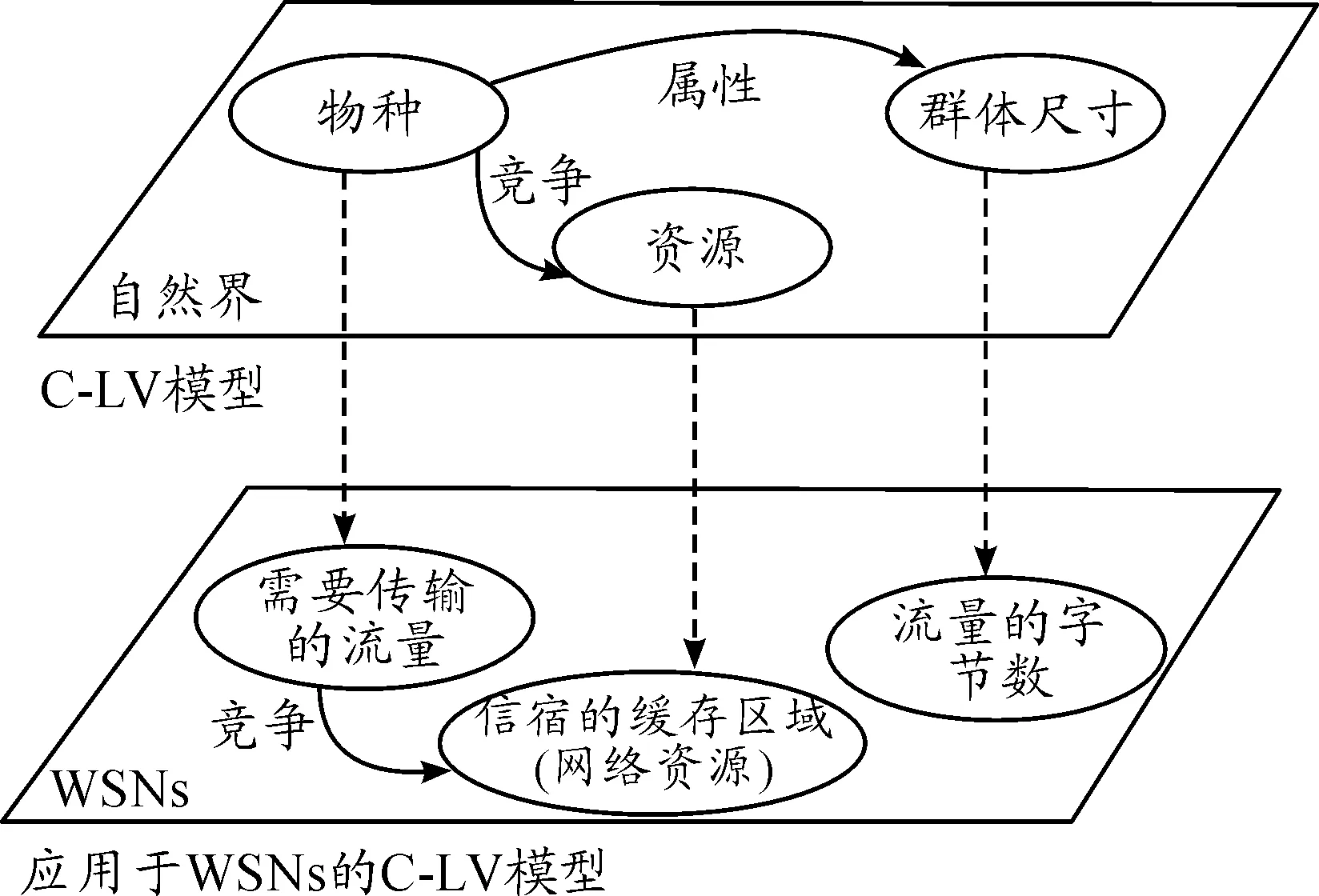
图3 应用于WSNs的C-LV模型
如图2所示,每个节点向信宿发送数据包(流量)。将每个节点看成竞争物种。且将信宿的缓冲容量看成每个物种的携带容量。而提出BICC算法的目的就是控制每个节点产生流量率,即动态调整流量率。
回顾到式(1),其反映物种竞争资源的关系。将C-LV模型应用于WSNs后,仍可构建等式(1)。考虑WSNs的网络特性,可设定以下约束条件:
首先,每个流量具有相同的携带容量,即每条流量的数据包尺寸相等:
Ki=K,∀i∈{1,2,3,…,n}
(2)
由于所有传感节点为同构节点,彼此影响相同。因此,满足式(3):
αij=α,∀i,j∈{1,2,3,…,n} andi≠j
(3)
且
αii=β,∀i∈{1,2,3,…,n}
(4)
因此,将式(2)、式(3)、式(4)代入式(1)可得:
∀i∈{1,2,3,…,n}
(5)
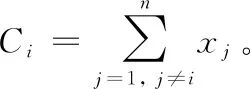
而式(5)的解可表示为
(6)
其中ω=K-αCi。式(6)表示第i条流量的字节数。若是单位时间所传输的字节数,则其反映了流量的传输率。
将C-LV模型应用于WSNs的目的在于使所有节点能够公平地竞争资源,而不是某单个节点独占资源。即系统能达到最稳定状态。依据特征值稳定理论:如果所有特征值均为非负数,则达到稳定。此外,仅当参数β>α>0时,才能获取式(6)的全局非负的稳定状态解,如式(7)所示:
∀i∈{1,2,3,…,n}
(7)
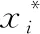
α(n-1)+β≥norβ-α≥n(1-α)
(8)
如果α≥1,则不等式(8)永远满足。综上所述,只要满足式(9),则可以保证各节点共存,达到最稳定状态。
1.3 粒子群优化
粒子群优化PSO是依据动物生存法则而产生的仿生算法。多个粒子共同行走,但无发生碰撞。原因在于:每个粒子服从群体,调整自己的位置和速度。
在PSO算法中,每个粒子代表一个优化群体目标的可行解。令f(x)表示目标函数。用X=(x1,x2,…,xN)、V=(ϑ1,ϑ2,…,ϑN)分别表示粒子群个体位置矢量、速度矢量,其中N表示群体数。并且依据式(10)、式(11)进行更新位置矢量和速度矢量:
X(t+1)=X(t)+V(t+1)
(10)
V(t+1)=ωV(t)+c1r1(P-X(t))+c2r2(G(t)-X(t))
(11)
其中P=(p1,p2,p3,…,pN)表示每个粒子个人最优解,而G表示全局最优位置。而惯性权重ω为速度的扩展因子。常数c1、c2决定P、G的权重。而r1、r2为两个随机数,且它们服从[0,1]的随机分布。
假定有N个粒子,每个粒子最大迭代次数为MaxIteration。每个粒子依据算法1进行更新位置矢量和速度矢量。算法1如图4所示。

图4 算法1设计图
引用PSO算法的目的在于:通过优化参数α、β,降低平均时延。当然,参数α、β必须满足式(9)。实际上,式(9)规定了α、β下限值。算法2如图5所示。

图5 算法2设计图
利用算法2产生目标函数f(α,β),其中M表示抽样的次数。尽管f(α,β)不能完全代表网络的平均时延,但是它与网络的平均时延呈线性关系。因此,最小化目标函数f(α,β)等同价于最小化平均时延。
2 性能仿真
2.1 仿真环境
利用NS3++软件建立实验平台。考虑星形拓扑网络,如图6所示。其中传感节点数为20。信宿节点的缓存容量这30 KB。抽样时间为1 s。同时引用基于CSMA的IEEE 802.11 MAC协议作为接入协议。最初,每个节点向信宿传输的速度为1 Kbps,随后,BICC算法控制各节点的传输速率。
2.2 性能分析
提出BICC算法的主旨在于自适应地调整节点的传输速率。因此,重点分析节点的传输速率,检测是否能调整节点传输速率。
为了更好地分析BICC调整速率的性能,采用逐步增加节点数的方法。最初,先增加5个传感节点(sensor1、sensor 2、sensor 3、sensor 4、 sensor 5),100 s后,再增加5个传感节点,直到添加了20个传感节点。因此,20个传感节点分了4段,为了简化描述,第1阶段用Sensor Node 1表述;第2阶段用Sensor Node 6表述;第3阶段用Sensor Node 11表述;而第4阶段用Sensor Node 16表述。

图6 星形的拓扑结构
图7显示了这4个阶段的控制速率的情况。从图7可知,节点的传输速率随节点数逐步在变化。图8将第1阶段的传输速率图进行了放大,其只显示了第1阶段5个传感节点的传输速率。
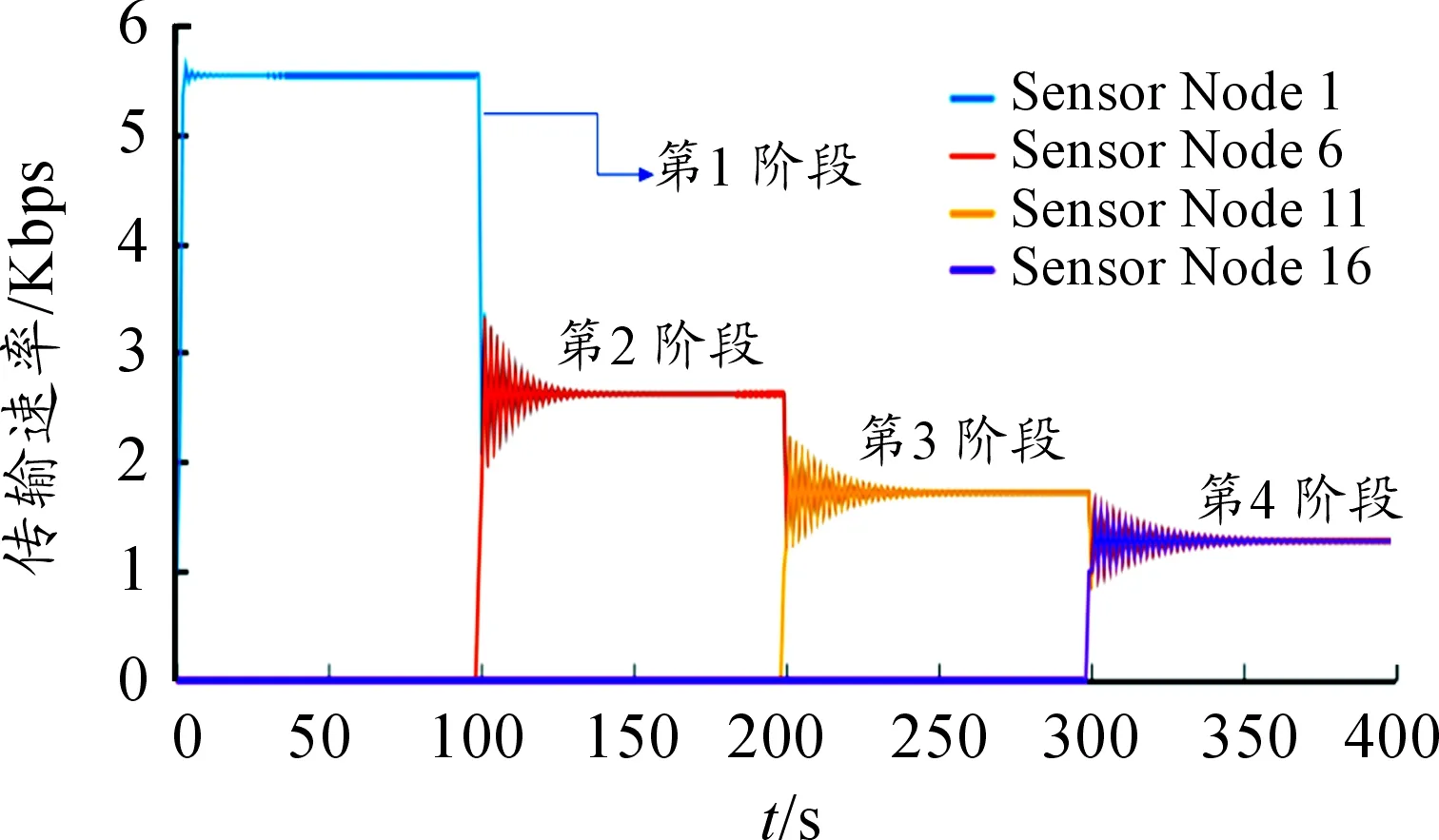
图7 基于BICC的流量控制
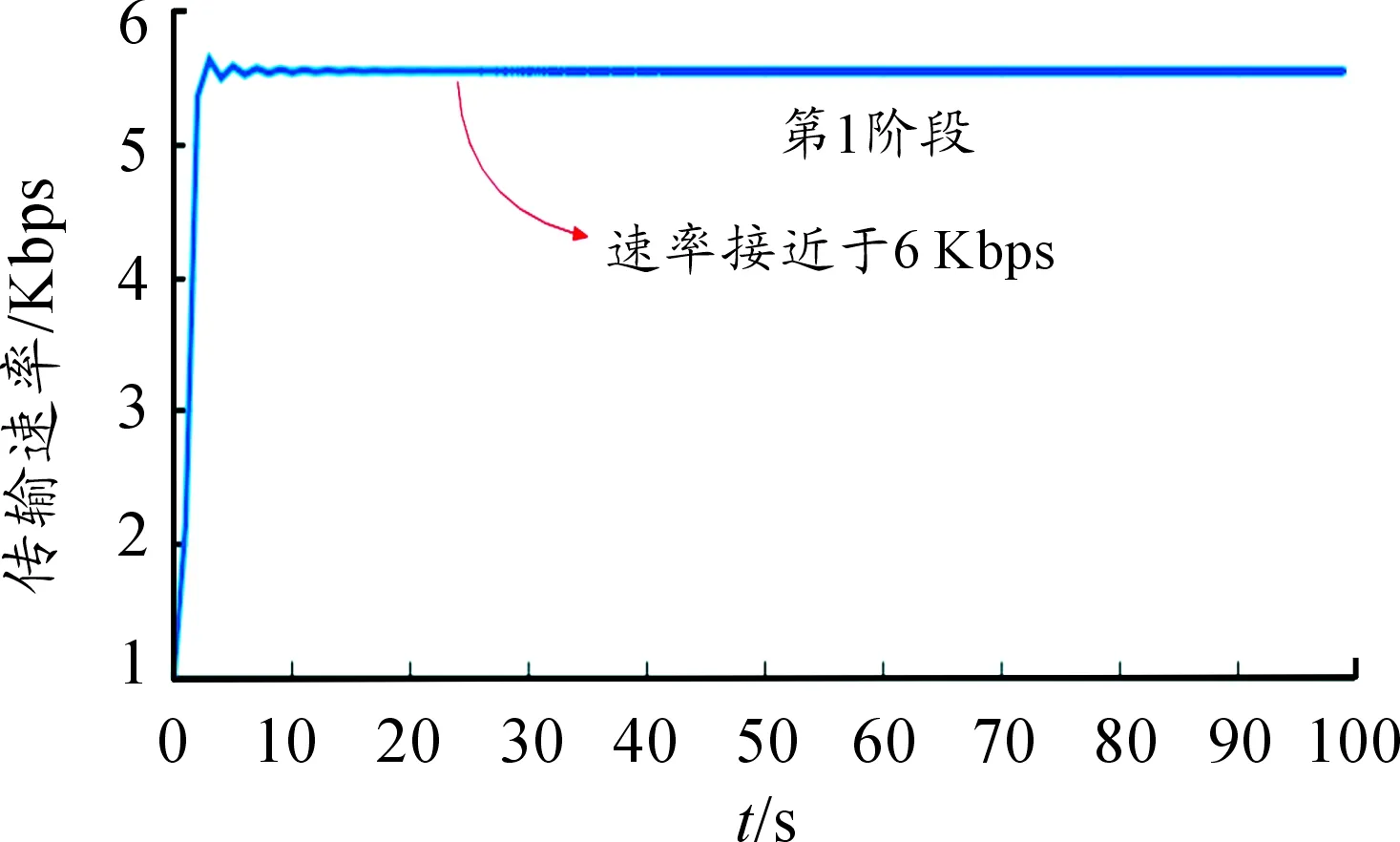
图8 第1阶段的传输速率
从图8可知,5个传感节点的传输速率接近6 Kbps,正好逼近于信宿的缓存容量30 KB。并且没有任何拥塞出现。这些数据说明,提出的BICC算法能够有效调整传输速率,并控制网络无拥塞。
图9显示了第2阶段10个传感节点的传输速率。从图9可知,BICC算法能够有效地调整传输速率:在前100 s,5个传感节点的传输速率约为5.5 Kbps,但当节点数增加至10个后,传输速率马上调整至近3 Kbps。
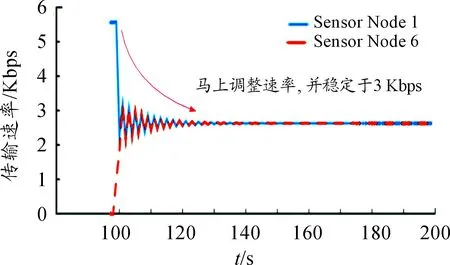
图9 10个传感节点的传输速率
最后,引用典型的流量控制算法,和式增加积式下降(Additive Increase Multiplication Decrease,AIMD)算法[8]与BICC算法进行比较。图10也显示了20个传感节点的传输速率情况。
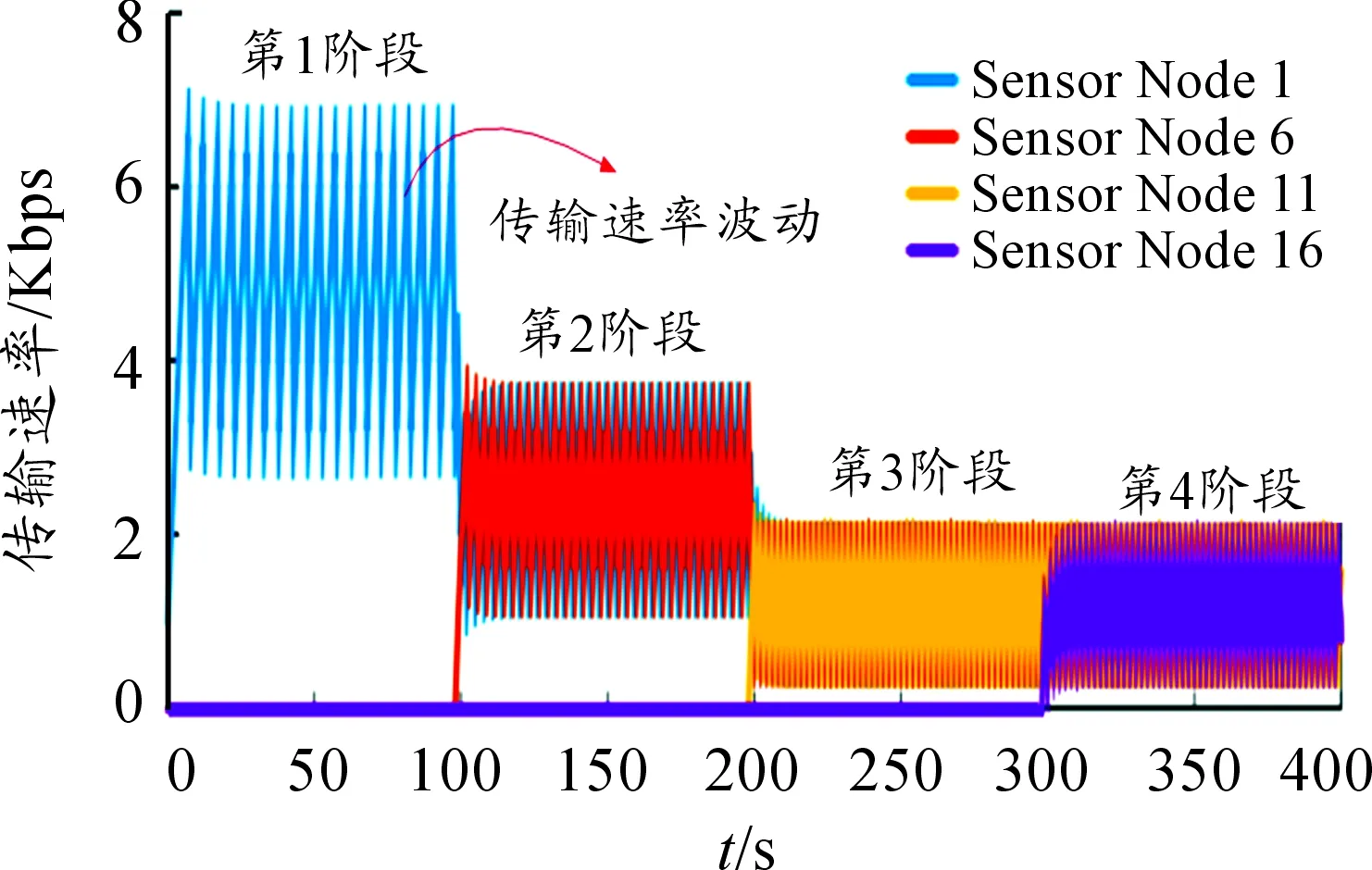
图10 基于AIDM的流量控制
从图10可知,AIDM算法所控制的传输速率波动大,这说明传感节点在传输数据时,出现拥塞。对比图5,不难发现,BICC算法能够有效调整传输速率,并达到稳定。
3 结论
针对WSNs网络拥塞问题,提出BICC算法进行拥塞控制。BICC算法引用C-LV模型解决WSNs的拥塞问题,进而维持节点间的公平。同时,利用PSO优化C-LV模型参数,进而使BICC算法能够自适应应对节点数的增加。
仿真结果表明:提出的BICC算法能够避免拥塞,维持高的数据传输速率,并使得节点的传输率达到最优的状态。后期将BICC算法应用到真实的工业系统,并分析它的性能,这将是后期的工作方向。
