基于Fluent的底部排气弹减阻特性数值模拟

朱越亭,马铁华,张红艳,沈大伟

(中北大学 仪器科学与动态测试教育部重点实验室， 太原 030051)

底部排气减阻增程是从曳光弹射击试验中得到启发的，其原理如下：弹丸飞行时，在弹丸后部形成低压区，产生底部阻力，在弹丸底部附加一个排气装置，向弹底低压区排入质量和能量，通过提高底压来减阻增程。底排减阻的空气动力学研究已经有将近70年的历史，底部排气弹的研制也有将近50年[1]。

目前，数值模拟方法是国内外研究底排减阻技术的主要手段之一。国内方面，史金光等[2]运用滑移网格技术进行底部排气弹三维流场的数值模拟；卓长飞等[3-4]对超声速底部排气弹底排真实气体流场以及底部排气弹底排真实气体底部二次燃烧现象进行了数值模拟；骆晓臣等[5]采用计算空气动力学和质点外弹道学耦合的方法求解底部排气弹的飞行弹道；谢利平等[6]建立了底排内弹道和外弹道模型，分析了底排装置结构参数和药剂燃速系数等对底部排气弹减阻增程效果的影响；罗盟等[7]采用标准k-ω湍流模型和有限速率化学反应燃烧模型对二维轴对称雷诺平均N-S方程进行了数值计算。国外方面，Subbareddy P等[8]和Shin J R等[9]先后采用分离涡数值模拟的方法对超声速飞行的底部排气弹进行了数值模拟；Charles J Nietubica[10]采用层流流动模型和层流燃烧有限速率基元反应模型，模拟了M864弹的二维轴对称流场；LEE Y K等[11]通过数值模拟带孔后体模型在马赫数为2.47时底部排气的流动特征，发现对应于最大的底排压力有一个使底阻最小的底排条件；Petri Kaurinkoski[12]和Jeong-Yeol Chor[13]分别采用k-ε、k-ω湍流流动模型和层流燃烧有限速率基元反应模型，模拟了155 mm弹的三维、二维流场；Choi J Y等[14]对含外部燃烧和中心推进喷射的底部排气弹的减阻特性进行了数值模拟。

区别于以往数值计算所采用的软件和方法，本研究以155mm弹为物理模型，运用前处理软件Gambit建立弹丸模型并进行网格划分，运用Fluent软件进行仿真计算，对有无底排的弹丸流场及其气动力参数进行分析，研究不同来流马赫数和攻角下弹丸的阻力系数和升力系数的变化规律，为底部排气弹的研究提供理论参考。

1 模拟方法

以155 mm弹为物理模型，弹丸由尖拱形母线的弹头部、圆柱弹身以及船尾组成，运用前处理软件Gambit建立弹丸模型和划分网格，弹丸表面网格的分布如图1所示。

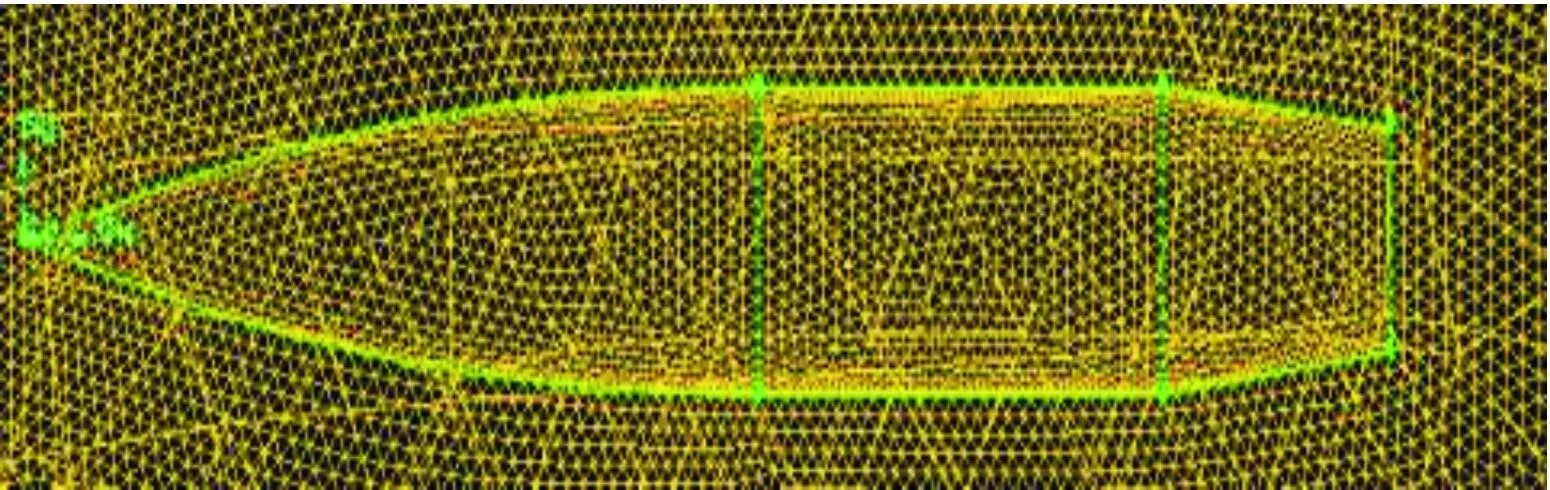
图1 弹丸表面网格分布

弹丸的计算域网格分布如图2所示，在运用Gambit划分网格时，Equisize Skew通过单元的大小计算歪斜度，绝大多数网格控制在0.4以内，以满足计算要求。设置壁面、对称面和压力远场的边界条件：其中壁面要求选择的面为弹体的壁面；对称面选择为计算域的截面和弹体的截面；压力远场选择大计算域除了界面的另外三个面。

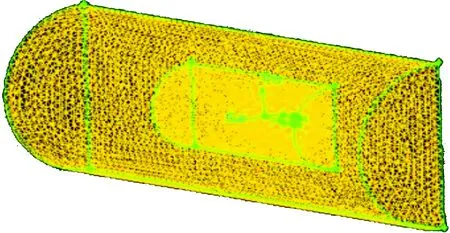
图2 计算域网格分布

网格模型确定后，将其导入Fluent软件中，数值模拟的具体相关参数均在该软件中修改。材料属性选择理想气体ideal-gas，萨兰德(sutherland)定律计算黏性。计算域外边界采用压力远场的边界条件，大气压为101 325 Pa，马赫数以及攻角的余弦和正弦值应根据具体模型来确定。湍流参数中的湍流黏度比(Turbulent Viscosity Ratio，TVR)保持为10。在大马赫数下柯朗数(Courant Number)为0.1-0.5，在小马赫数下为默认值；Flux Type在小马赫数情况下为Roe-FDS，在大马赫数的情况下为AUSM。选择二阶迎风格式。

2 数值模拟结果与分析

2.1 无底排气动特性数值模拟

无底排状态下，来流马赫数分别为1.5、2.0、2.5、3.0、3.5，攻角分别为0，2，4，6(单位度)共计20种状态。马赫数为2.0，攻角为0的弹丸密度和压力等值线图如图3所示。

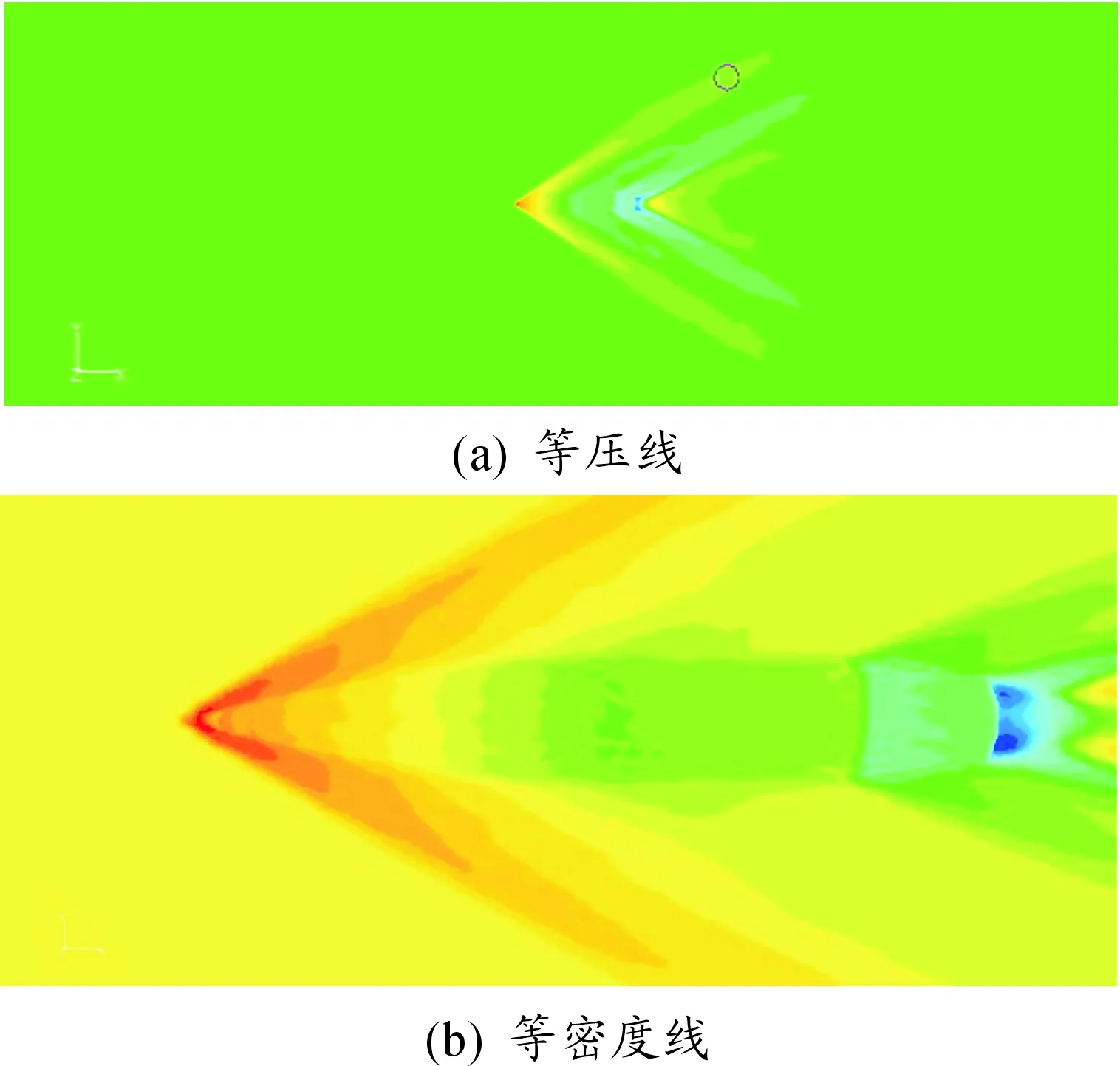
图3 Ma=2.0，α=0°的等值线

弹丸超音速飞行时，气流在弹头部产生斜激波，气流经过激波后沿弹身向下流动，当气流到达弹丸船尾角时，由于弹尾物面的折转，气流开始膨胀，产生膨胀波。当气流达到弹丸底部时，物面再一次迅速折转，气流再一次膨胀，产生剧烈的膨胀波。气流继续向下游流动，并逐渐恢复来流方向，在弹丸的尾迹区由于气流的压缩产生再压缩激波。

由密度和压力的大小分布得知，气流通过激波后压力与密度迅速增大，图示弹头部呈现红色。气流继续朝弹丸的底部流动,由于弹底部气体的低速回流，并且无外流的补充，产生一个低压区，低压区的存在导致弹丸底阻的形成。

图4为马赫数1.5、3.5，攻角0°时的等压线图。随着来流马赫数的增加，气流压缩变得更加强烈，弹体表面与激波面夹角逐渐减小，导致激波会逐渐贴近弹体表面。

当来流有攻角时，以来流马赫数2.0，攻角6°时为例，流场变化如图5所示。弹丸迎风面的激波面与物面夹角随攻角的增大而减小，弹丸背风面的激波面与物面夹角随攻角的增大而增大。此外，弹丸底部流场在攻角变化时，迎风面的尾迹区受到的挤压随攻角增大而越明显，背风面的尾迹区向下挤压迎风面尾迹区的程度随攻角增大而增强。

弹丸的阻力系数(Cd)和升力系数(Cl)随来流攻角及马赫数变化曲线如图6所示。

图4 不同马赫数的等压线

图5 Ma=2.0，α=6°的等压线

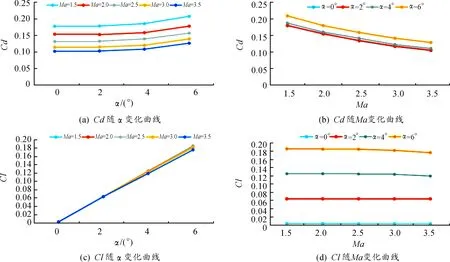
图6 阻力系数和升力系数变化曲线

随来流攻角的增大，弹丸的阻力系数呈抛物线性增长趋势。在同一攻角下，弹丸的阻力系数随来流马赫数的增大不断减小，呈抛物线性减小趋势。

弹丸升力系数随着攻角的增大呈线性增长的趋势。在同一来流攻角下：当攻角为0°时，弹丸升力系数基本不随来流马赫数的变化而变化，维持为0。当弹丸有攻角且攻角比较小的情况下如α=2°时，升力系数随马赫数的增加呈减小趋势，但变化不是很明显，当攻角相对较大的情况下如α=6°时，其升力系数随来流马赫数的减小更为明显。

2.2 有底排气动特性数值模拟

在无底排的基础上修改边界条件，简化物理模型，通过在弹底排出速度v=25 m/s的气体，分析对底部流场、气动力系数和减阻的影响。

以来流马赫数2.0，攻角0°时绕弹丸流场的压力和密度等值线图为例来说明有底部排气时的弹丸流场特性，如图7。

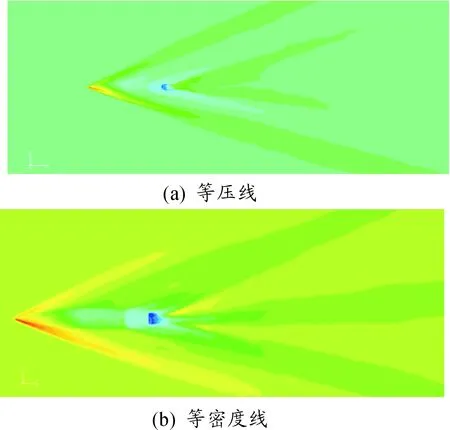
图7 Ma=2.0，α=0°的等值线

加入底部排气后，弹丸前部流场结构变化不大，弹丸底部折转处的膨胀波明显减弱。这主要是由于底排气体的补充，剪切层被抬高，气流流经弹底时膨胀波减弱，折转角减小。此外，底排高能气体填充底部低压回流区，将弹丸底部尾迹区明显后推，导致再压缩激波位置后移。密度等值线中，由于补充进入的气体，弹丸底部低压区的剪切层被抬高，气流流经尾部时的折转角明显减小。弹丸底部补充的气体改变了弹丸底部的流场结构。

来流马赫数变化时，以马赫数1.5和2.5为例，弹丸流场变化情况如图8所示。气流受到的压缩作用随着马赫数的增加而更加强烈，产生的激波角慢慢减小，尾迹区的再压缩激波和弹尾的膨胀波的变化趋势也相同。弹丸周围流场的压力和密度相较低马赫数也有较大提高。弹丸底部受到底排气体的影响，尾迹区都向后推移，根据等值线图可以看出，在高马赫数的情况下，弹丸底排气体于尾迹区的后推效果要好于低马赫数的情况。

当来流攻角变化时，以来流马赫数2.0，攻角6°时的流场图为例，如图9所示。弹丸迎风面的激波角减小，背风面的激波角增大，在弹丸有攻角时弹丸尾迹区流场结构不再对称，迎风面尾迹区域被背风面尾迹区域挤压明显，背风面底部流场由于受到外流的挤压让整个弹丸底部排气区域向迎风面的底部区域靠近。背风面弹丸尾迹区后推作用相对于迎风面被削弱。

图8 不同马赫数的等压线

图9 Ma=2.0，α=6°的等压线

弹丸的阻力系数(Cd)和升力系数(Cl)随来流攻角及马赫数的变化曲线如图10所示。

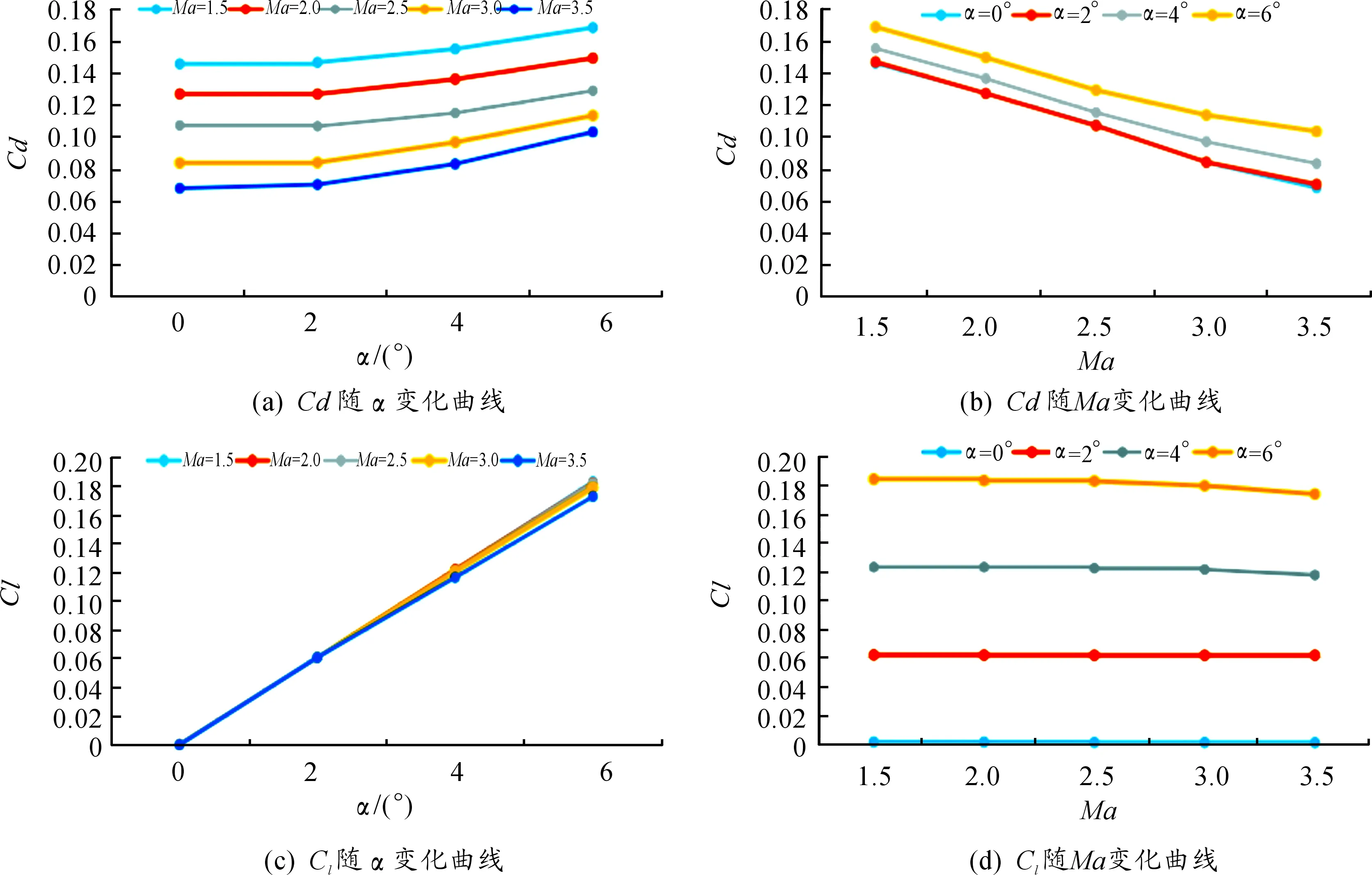
图10 阻力系数和升力系数变化曲线

弹丸的阻力系数随攻角的增大呈抛物线性增长，随着来流马赫数的增大呈抛物线性减小。与无底部排气时弹丸阻力系数的变化趋势相同。

弹丸升力系数随攻角增大呈线性增长，0°攻角时升力系数不随马赫数增大而改变，均维持在0左右。攻角增大后，升力系数随马赫数的增加呈现出线性减小趋势，但变化趋势不是很明显。

2.3 有无底排情况计算结果对比

图11为任取同一来流马赫数下，加入底排前后弹丸气动力诸系数随来流攻角的变化。

弹丸升力系数都随攻角的增大呈线性增长的趋势，有无底排前后大小几乎没有发生变化，这是因为弹丸的底部阻力是由于弹丸底部所受到压力远低于来流导致的，并没有直接作用于弹体上,对于弹丸的法向力和轴向力的影响很小。弹丸的全弹阻力系数有较大改变，加入底排后，弹丸的阻力系数大幅下降，说明底排减阻效果明显。

作者还研究了有无底排状态下的阻力系数。将加入底排前后的阻力系数整理比较之后，得到阻力系数的最高减阻率达到34.8%，最低达到14.8%。上面两个数据可以说明，底排气体减小了弹丸的底阻，使得弹丸的整体阻力下降，射程增加。由此可见加入底排气体确实可以降低弹丸阻力，从而实现增程的目的，验证了理论的正确性。

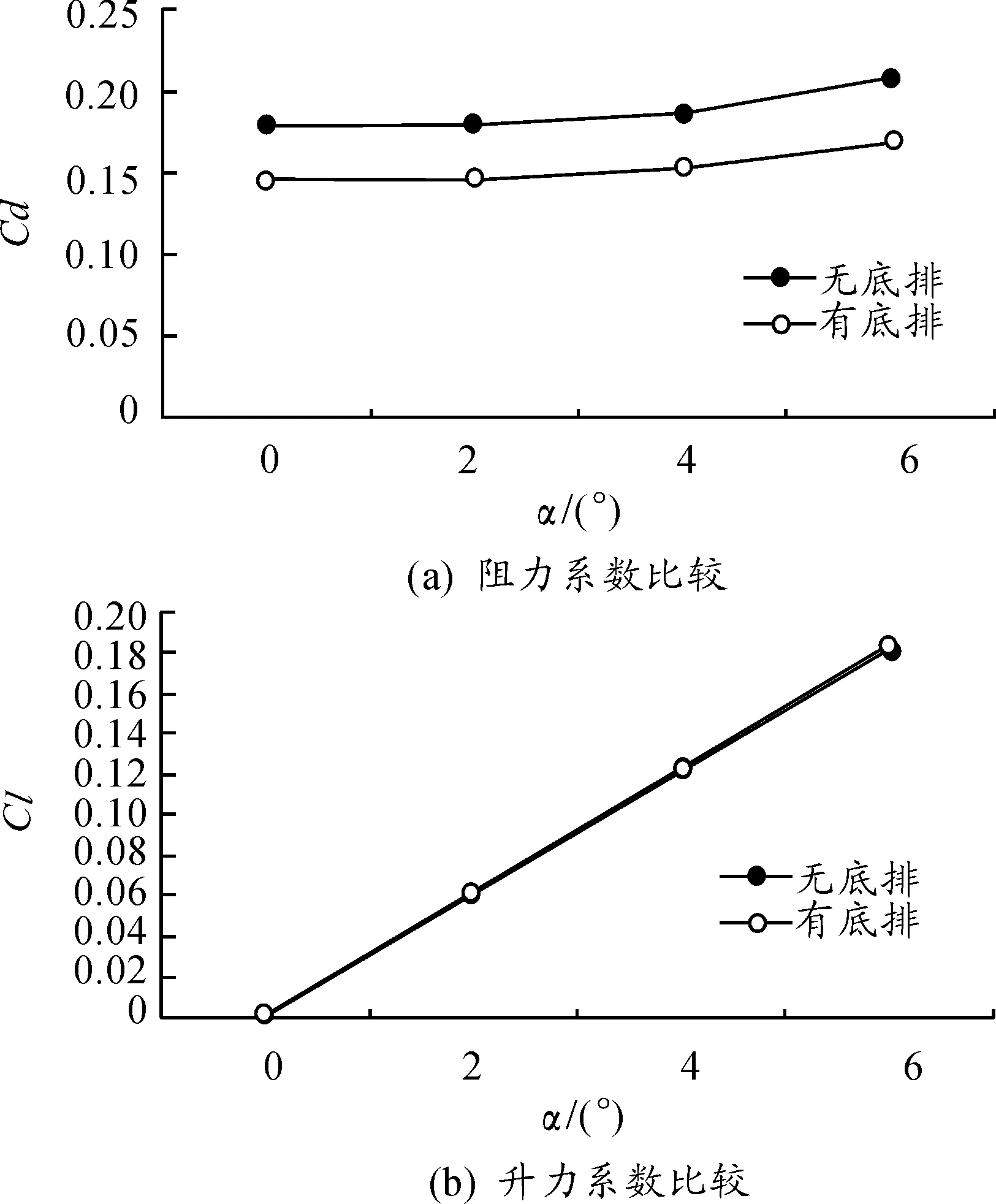
图11 底排前后的阻力系数和升力系数

3 结论

1) 超音速来流下，阻力系数随来流攻角的增大呈抛物线性增大，随来流马赫数的增大呈抛物线性减小。

2) 超音速来流下，升力系数随来流攻角的增大线性增大，随来流马赫数的增大而减小，攻角越大减小幅度越明显。

3) 弹丸在加入底排前后，升力系数无明显变化，阻力系数大幅下降，达到减阻效果，且阻力系数的最高减阻率达34.8%，结果符合空气动力学规律，验证了底部排气弹减阻增程的理论依据，为底部排气弹的研究提供参考。