基于直觉模糊集和VIKOR法的多目标威胁评估
2019-07-05张明双徐克虎李灵之
张明双,徐克虎,李灵之
(陆军装甲兵学院, 北京 100072)
科学技术的井喷式发展促进了武器装备的不断更新换代,作战双方对战场目标的侦查感知能力不断增强,战场透明度显著提高,面对海量的战场信息,指挥员要想实现准确的指挥决策往往力不从心。因此,建立合理的评估决策模型,对复杂地面战场多个目标进行及时准确的威胁评估以辅助指挥员高效的指挥决策,具有重大的军事意义。
多目标威胁评估问题的本质是多属性决策问题,近年来取得了丰富的研究成果。文献[1]融合灰色理论与层次分析法,客观有效地对合成营多装备体系进行评估与排序。文献[2]将区间数理论与灰色理论相结合,为舰艇编队对来袭多目标反导提供重要参考。文献[3]提出融合直觉模糊集和证据理论的方法对空战中多目标进行评估排序,证明了模型的有效性。文献[4]采用熵权与层次分析组合加权的方法,结合逼近理想解法(Topsis)对空战多目标进行威胁评估,取得了较好效果。
根据上述典型文献可以看出,以上方法在解决多目标威胁评估问题时各有优势,但仍有不足之处:
1) 赋权过程中,决策者易将专家经验当作绝对权威,较少考虑专家知识结构和专业水平不均衡所造成的影响,即没有考虑专家的相对权重。
2) 没有考虑专家个人偏差对最终结果的影响,对同一指标中的过高和过低评价给予一定的抑制,即没有考虑位置权重。位置权重是指对于同一指标下的多位专家的评价,按照由小到大的顺序排列,对过低和过高的评价赋予较少的权重,对中间的评价赋予较多的权重,以使综合评价向多数评价集结。
3) 一般决策者要求专家给出的都是指标精确值或者区间值,然而专家决策时更倾向于用自然语言(如好,较好,一般,较差)来表达对指标模糊性和不确定性的偏好。
4) 在进行多属性决策时,若指标体系是含有定性和定量指标的混合型体系,一般会将数据转化为同种类型后进行求解,但这一过程会导致部分信息的丢失和失真,评估结果易产生偏差。
针对以上评估决策中存在的问题,提出一种基于直觉模糊集(Intuitionistic Fuzzy set,IFS)和多准则优化妥协决策(Vlse Kriterijumska Optimizacija I Kompromisno Resenje,VIKOR)相结合的威胁评估模型。利用直觉模糊集能够综合反映支持、中立和反对3个不同角度信息,在处理模糊性和不确定性问题方面更细腻、客观的优势,综合考虑多名专家的相对权重和所给数据的位置权重,结合直觉模糊混合加权集结算子求解最终权重。尝试将VIKOR法引入地面战场多目标威胁评估中,不仅能够对混合型指标数据直接进行集结,而且能妥协最大化“群体效益”和最小化“个别遗憾”,进而确定最终的折中方案[5]。最后通过实例验证、灵敏度分析和对比分析说明了该方法的合理性与有效性。
1 直觉模糊集基础知识
设X是非空有限论域,则对论域中1个直觉模糊集A,可记为
A={〈x,μA(x),νA(x)〉|x∈X}
其中,uA(x):X→[0,1]和νA(x):X→[0,1]分别表示元素x属于集合A的隶属度和非隶属度,且0≤uA(x)+νA(x)≤1,x∈X。对于∀x∈X,πA(x)=1-μA(x)-νA(x),表示x属于集合A的不确定度或犹豫度。
两个模糊集A={〈x,μA(x),νA(x)〉|x∈X}和B={〈x,μB(x),νB(x)〉|x∈X},模糊运算关系为
(1)A+B={〈x,μA(x)+μB(x)-μA(x)μB(x),νA(x)νB(x)〉|x∈X};
(2)AB={〈x,μA(x)μB(x),νA(x)+νB(x)-νA(x)νB(x)〉|x∈X};
(3)λA={〈x,1-(1-μA(x))λ,(νA(x))λ〉|x∈X};
对于论域X={x1,x2,…,xn}上两个模糊集A={〈xj,μA(xj),νA(xj)〉|xj∈X}和B={〈xj,μB(xj),νB(xj)〉|xj∈X},它们之间的hamming归一化距离为
|πA(xj)-πB(xj)|)
(1)
记直觉模糊集A=〈μ,ν〉的得分值M(A)和精确值Δ(A)分别可表示为

则2个直觉模糊集Ai和Aj的排序规则如下[6]:
(1)若M(Ai)>M(Aj),则:Ai>Aj
(2)若M(Ai)=M(Aj),则:
a) 若Δ(Ai)=Δ(Aj),则Ai=Aj;
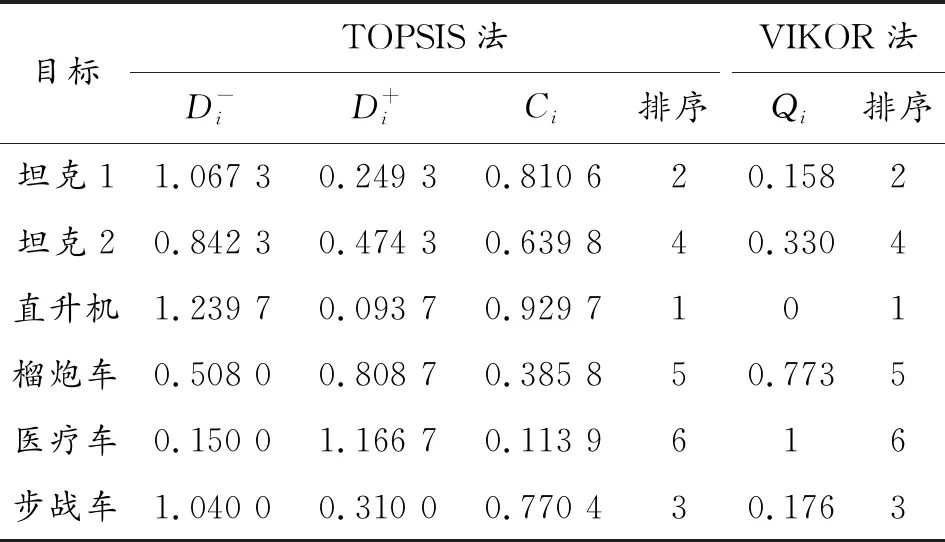
b) 若Δ(Ai)<Δ(Aj),则Ai c) 若Δ(Ai)>Δ(Aj),则Ai>Aj。 (2) 本文把直觉模糊理论拓展到VIKOR决策方法中,建立了多目标威胁评估模型,模型综合考虑多名专家的相对权重和所给数据的位置权重,利用直觉模糊混合加权算子对VIKOR法进行加权改进,模型评估过程如图1所示。 图1 模型评估过程框图 影响战场目标威胁大小的因素很多,本文在给出预选指标集的基础之上,结合作战实际和专家筛选结果统计分析,最终确定了火力打击能力、机动突击能力、防护能力、相对距离、相对速度、相对方位6个主要评估指标,建立了多目标威胁评估指标体系如表1所示。其中,定性指标可由模糊语言来描述,然后依据表2的转化关系表进行量化。定量指标可直接获取具体的数值。 表1 评估指标体系 表2 模糊语言与直觉模糊数转化关系 假设共有p名专家,m个待评估目标,n个评估指标。则专家集T=(t1,t2,…,tp),目标集X=(x1,x2,…,xm),指标集O=(o1,o2,…,on),权重的确定步骤如下: (1)获取专家对指标的直觉模糊集评价矩阵F=(Fij)p×n=〈uij,νij〉p×n。 其中Fij表示第i个专家对第j个指标的直觉模糊集评价。 (2)确定专家权重。专家权重可根据专家的专业水平和工作经验、研究方向等因素综合考虑,可采用层次分析法、相对比较法、德尔菲法等方法或直接由决策者给出专家权重向量ω=(ω1,ω2,…,ωp)。因为不是本文讨论的重点,这里不再赘述。 (5)确定位置权重。多个专家对同一指标进行重要度评判时,评判数据可能会因为专家经验不同而出现较大偏差,利用位置权重对过高或过低评判进行抑制,可消除部分人为因素的影响,位置权重可用二项系数法[9]来确定,计算公式为 (3) k为按排序规则排序后的位次,p为专家数量。由公式可知,排序位次越小或越大,权重值越小。 (4) 影响多准则优化妥协决策法(VIKOR)是南斯拉夫Opricovic教授于1998年提出的一种解决多属性决策问题的有效方法[11],近年来逐渐兴起并在很多领域应用广泛[12-15]。VIKOR法能够对混合型的决策矩阵直接进行计算,并能综合考虑群体效益的最大化和个体遗憾的最小化,进而确定妥协后的折中方案,具有更好的灵活性和适应性。其决策步骤如下: 1) 构建混合评估决策矩阵。确定各个目标在不同指标下的属性值,属性值为模糊语言的,按照表2转化为直觉模糊数,属性值为精确数值的需要标准化,构成混合决策矩阵Y=(yij)m×n。 2) 确定正理想解和负理想解。对于效益型指标: 当yij为直觉模糊集时, 当yij为精确数值时, 对于成本型指标: 当yij为直觉模糊集时, 当yij为精确数值时, 3) 计算第i个待评估目标的群体效益值Si和个体遗憾值Ri (5) (6) 其中,Wj表示指标的最终权重,直觉模糊集的距离d可由公式(1)求得,精确数的距离可直接求差的绝对值。 4) 计算妥协折中值Qi,确定威胁度排序 (7) 其中,ν表示决策者对群体效益和个体遗憾的折中系数,如果ν>0.5表明决策时更偏向整体效益,如果ν<0.5表明决策时更偏向个体偏差,ν=0.5表明决策时不存在明显偏好。本文取ν=0.6,即兼顾群体效益和个体遗憾的同时,稍偏向大多数群体,这也符合客观决策实际。妥协折中值Qi越小表示目标威胁度越大。 假设在一次作战演习中,我方通过侦查感知装备发现在不同距离和方位上有敌合成分队的6个目标(坦克1、坦克2、直升机、榴炮车、医疗车和步战车),并得到相关原始数据如表3所示。由原始数据构建混合决策矩阵Y。为保证评估的准确性,本文找了相关领域的5名专家给出指标的直觉模糊集评价数据如表4所示。 表3 目标原始数据 表4 专家对指标的评判矩阵用数据 令专家权重为ω=(0.2,0.25,0.18,0.15,0.22),得到加权并按规则排序后的直觉模糊集矩阵为 利用式(3)计算位置权重为w=(0.062 5,0.25,0.375,0.25,0.062 5),结合式(2)直觉模糊混合加权集结算子,计算出最终集结后的指标直觉模糊集评价矩阵A: A=(〈0.821,0.133〉,〈0.575,0.175〉,〈0.450,0.282〉, 〈0.752,0.136〉,〈0.518,0.238〉,〈0.680,0.160〉) 利用式(4)转化为精确数值并归一化得到最终权重: W=(0.190,0.165,0.134,0.186,0.149,0.177) 由混合决策矩阵求出正负理想解为 y+=(〈0.95,0.05〉,〈0.95,0.05〉,〈0.85,0.1〉, 0.110,0.308,0.067) y-=(〈0.15,0.75〉,〈0.5,0.35〉,〈0.25,0.65〉, 0.274,0.038,0.333) 利用式(5)、式(6)、式(7),分别计算出各个目标的群体效益Si、个体遗憾Ri和妥协折中值Qi如表5所示。 表5 目标的S,R,Q值 由结果可知,威胁度大小排序为:直升机,坦克1,步战车,坦克2,榴炮车,医疗车。分析原始战场态势可知,直升机火力强和机动性很强,相对速度高,威胁最大。坦克1火力、机动和防护都较强,距离较近,相对方位小,威胁次之。步战车比坦克2机动性强,距离近,相对速度高且相对方位小,威胁比坦克2要大。榴炮车虽然火力强,可机动性弱,距离较远,相对方位较大,所以威胁较小。医疗车火力弱,距离远,威胁最小。实例仿真结果较为合理,符合战场客观实际。 在VIKOR方法中,群体效益和个体遗憾的折中系数ν对妥协折中解Q的结果影响较大,不同的ν取值所得到最终目标威胁排序也会有差异。本文将ν∈[0,1]以0.1为一个标准间隔进行11次取值,得到11组不同的妥协折中解矩阵。通过对11组妥协解矩阵进行比较,分析不同的ν值对威胁排序结果的影响,以考察所建模型的稳定性。不同的ν值对威胁排序结果的影响如图2所示。 图2 不同折中系数下的目标威胁排序 由敏感度分析结果可知:在不同的ν值下,直升机、坦克2、榴炮车、医疗车的威胁度排序基本不发生变化,当ν≤0.2时,步战车威胁大于坦克1,当ν≥0.3时,坦克1威胁大于步战车。这是因为不同的折中系数ν值表明决策者对群体和个体的侧重不同,评估结果会略有差异。综合来看,模型总体上具有较强的稳定性,评估结果合理有效,并能兼顾指挥员的主观偏好,具有更大的灵活性。 VIKOR法与TOPSIS(逼近理想点)法都需要求解决策矩阵的正负理想解,所不同的是,VIKOR法着重考虑正负理想解之间的相关性,而TOPSIS法考虑待评估对象与理想解的相对贴近度,贴近度越大,目标威胁越大。本文利用TOPSIS法得出目标威胁评估结果,与所建立的直觉模糊VIKOR模型进行对比分析,进一步证明模型的有效性。其贴近度计算方法如式(8)所示: (8) 表6 两种方法结果对比 由表6结果可知,VIKOR法与TOPSIS法的目标威胁评估结果高度一致,对比结果进一步表明了建立模型的准确性与合理性。 本文针对地面战场多目标威胁评估与排序的问题,建立一种将直觉模糊理论与VIKOR法相结合的多属性决策模型。模型利用直觉模糊集在处理模糊性问题更细腻、客观的优势,兼顾多名专家的知识结构和专业水平的偏差对评估结果的影响,综合考虑专家的相对权重和数据的位置权重,采用直觉模糊混合加权集结算子对数据进行集结,从而求出最终权重。引入VIKOR法对地面战场多目标进行威胁评估,并结合作战演习实例验证了模型的合理与有效性。最后分析了不同折中系数ν下的目标排序情况,并将结果与Topsis法进行对比,再次说明了模型的稳定性与正确性。实例表明,本文的评估过程简洁有效,能够为指挥员作战决策提供重要参考。

2 基于IFS-VIKOR法的多目标威胁评估模型

2.1 指标体系的确定

2.2 指标权重的确定


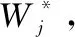
2.3 VIKOR法求得最终评估结果

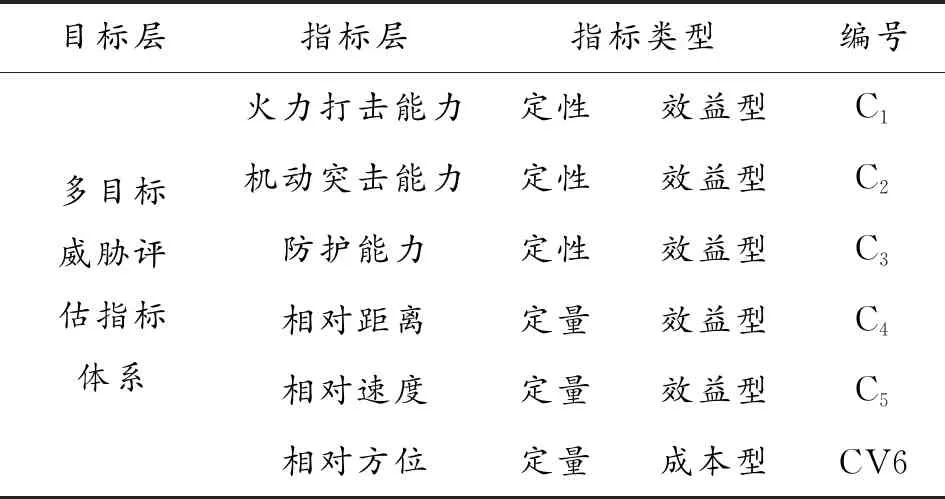
3 实例仿真



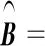

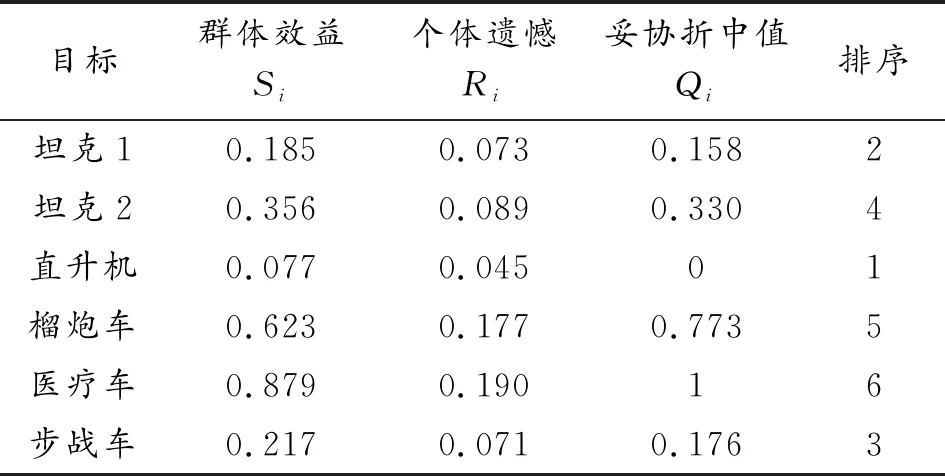
4 结果分析
4.1 敏感性分析

4.2 对比分析
5 结论
