高超声速滑翔再入定向定速打击末制导算法
2019-07-05王荣刚贾生伟
王荣刚, 许 志, 唐 硕, 贾生伟
(1. 西北工业大学 航天学院, 西安 710072; 2. 南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016;3. 中国运载火箭技术研究院,北京 100076)
0 引 言
高超声速滑翔再入飞行器要实现对目标的精确打击,其制导系统必须在复杂的热流、动压、过载及视场等过程约束条件下,实现对飞行器速度方向及大小的管控,这是一项极具挑战的制导难题。为了保证导引头的探测精度并提高突防能力,要求对目标进行垂直打击。对于定向打击问题,国内外研究[1-4]方法主要分为两类:①在比例导引的基础上通过设计附加项来实现[5-6];②通过调节比例系数来实现[7-8]。然而在高超声速飞行和复杂的过程约束条件下,同时考虑到机动减速及控制系统稳定性的影响,上述两种方法难以实现在有限的时间内完成弹道下压并实现定向打击。
飞行器在再入过程中采用合理的机动方式实现落速管控,以保证飞行器探测系统正常工作并降低其需用过载,是其再入制导的核心问题。目前再入制导主要集中在高升阻比气动布局的远距滑翔制导研究[9-11],针对本文所研究的具有低升阻比气动布局的短距滑翔制导减速控制方法主要分为数值预测制导[12-15]和理想速度曲线方法[16-17],其核心思想都是采用诱导阻力对飞行器进行减速。数值预测制导主要通过在一个或多个制导周期内对弹道积分以获得终端落速和落角来对制导指令进行修正,该方案制导精度高,但计算量较大且无法保证校正算法在每个制导周期内收敛。而理想速度曲线给出了一种具有解析形式的速度指令生成方法,该方法计算速度快,但由于其模型精度低致使其落速控制精度不高。可见设计一种能够在较短滑翔距离实现精准减速且在线计算量较小的减速方法是当务之急。
针对以上问题,本文提出了一种具有落角约束和减速控制能力的低升阻比高超声速滑翔飞行器再入打击末制导策略。为便于飞行器对目标进行定向定速打击,首先将弹道分为弹道调整段和末端攻击段,弹道调整段通过跟踪在速度—高度空间在线设计的参考轨迹来实现初步大幅减速以及满足末端攻击段的交班条件。针对在末端攻击段引入角度控制指令会导致弹道变化剧烈、飞行器弹道无法及时下压以致脱靶、导引头视场丢失目标等问题,提出了一种根据导引头垂直视场偏差调节的变角偏差反馈系数偏置比例制导方法。在该制导方法的基础上,通过对弹道倾角及攻角进行估计,建立了一种基于高度修正的末端攻击段速度指令生成方案。
1 制导问题及实现方案
本文以潘兴II再入制导为研究对象(图1为潘兴II典型弹道),其制导任务是在给定飞行器的初始条件和复杂过程约束条件下导引飞行器由再入点无动力滑翔至目标处,同时满足终端脱靶量、落速及落角、导引头视场捕获要求。
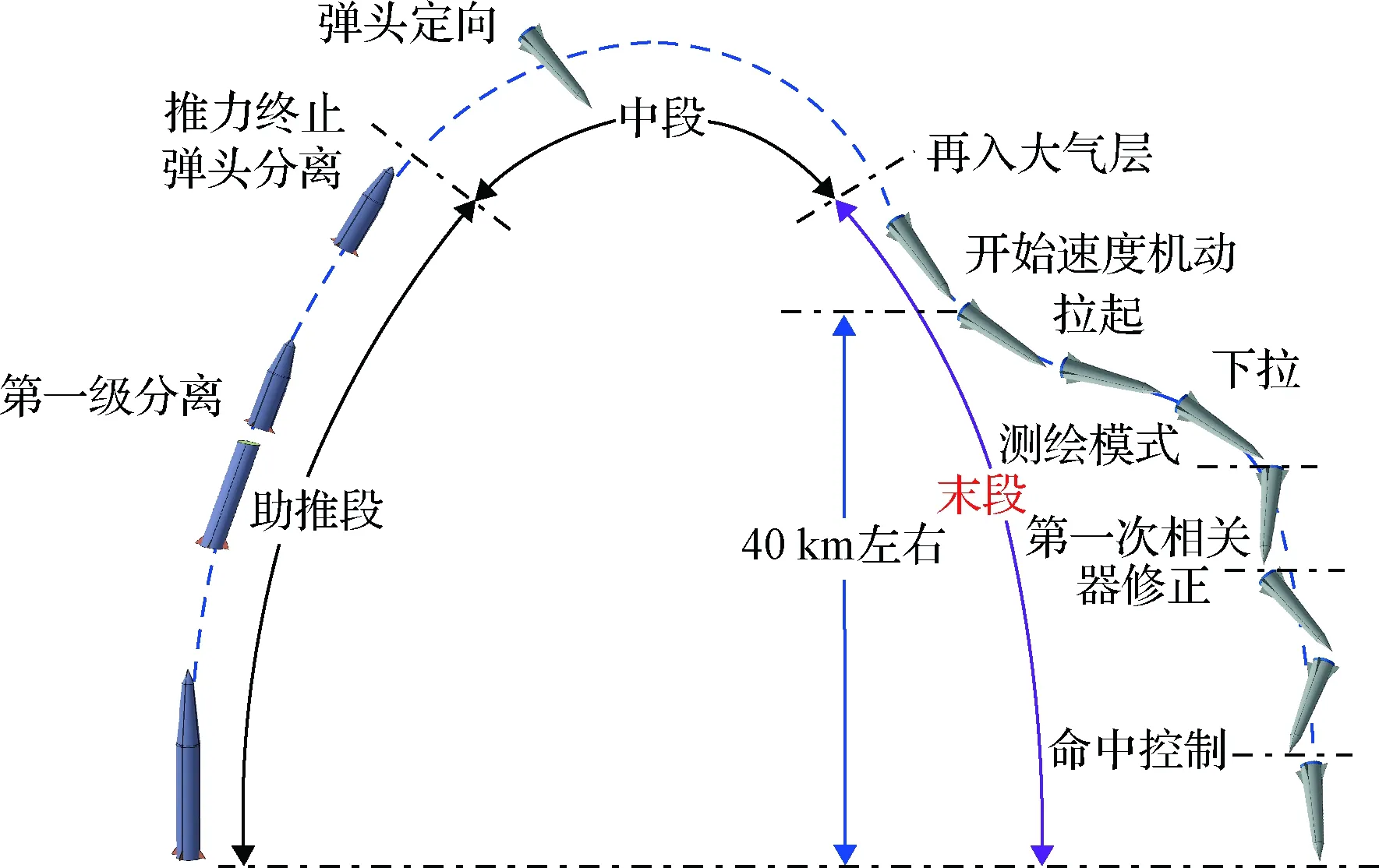
图1 潘兴II典型弹道Fig.1 The typical trajectory of Pershing II
1.1 滑翔再入打击
由于飞行器末段再入高度较低(h>40 km)且再入航程较短(s<100 km),飞行器直接采用俯冲攻击的方式对目标进行打击,导致制导方案对初始条件要求极为苛刻。此外,由于其以最大正攻角先将弹道进行拉升,再以最大负攻角的方式下压弹道,会导致飞行器缺乏额外的机动能力应对突发情况。为解决以上问题,可通过以下两种手段进行改进。
1)增加弹道调整段。如图2所示,可在原有末端攻击弹道基础上增加滑翔距离,采用拉升俯冲的方式对目标进行攻击。由于增加了滑翔距离,飞行器无法利用比例导引对目标展开直接攻击,需要在末端攻击前增加弹道调整段,以增强飞行器的弹道调整能力,实现初步大幅度控速,及满足末端攻击段交班条件的要求并给飞行器提供较为宽松的再入初始条件。
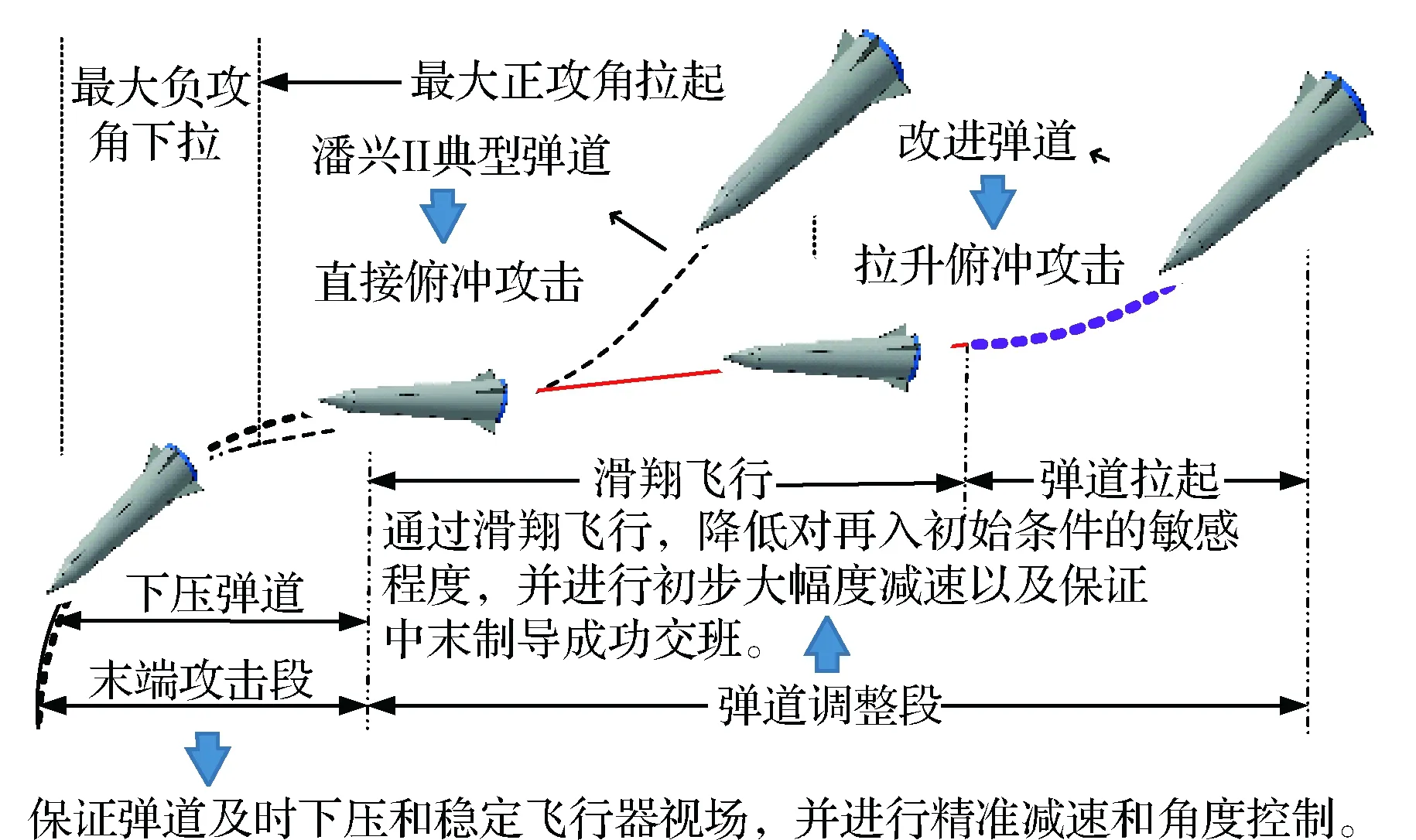
图2 改进弹道方案Fig.2 The trajectory amendment scheme
2)改善弹道下压方式。由于要在短时间内完成大幅度拉升下压机动,极易造成飞行器在进行弹道下压时掠过目标造成脱靶及使导引头丢失视场。为解决传统主升力朝上方式弹道下压速度较慢且机动幅度较大等问题,文献[18]提出了翻身下压的方式,可实现较大正攻角飞行,也有利于热防护。然而,翻身下压也加剧各通道(气动、运动、惯性)之间的耦合,使得飞行器的非线性、时变性问题变得更显著。为解决以上问题,本文在末端攻击段采用了变角偏差反馈系数的方法,完成弹道下压并保证对视场的控制(如图3所示):在末端攻击段初期,由于加入了角度控制,弹道剧烈变化,造成垂直视场偏差比较大,可通过减小角偏差反馈系数来降低角度控制指令对弹道的影响幅度,从而保证弹道及时下压以及稳定导引头视场;在末端攻击段中后期,垂直视场偏差逐渐变小,可增大角偏差反馈系数,从而保证角度控制精度。
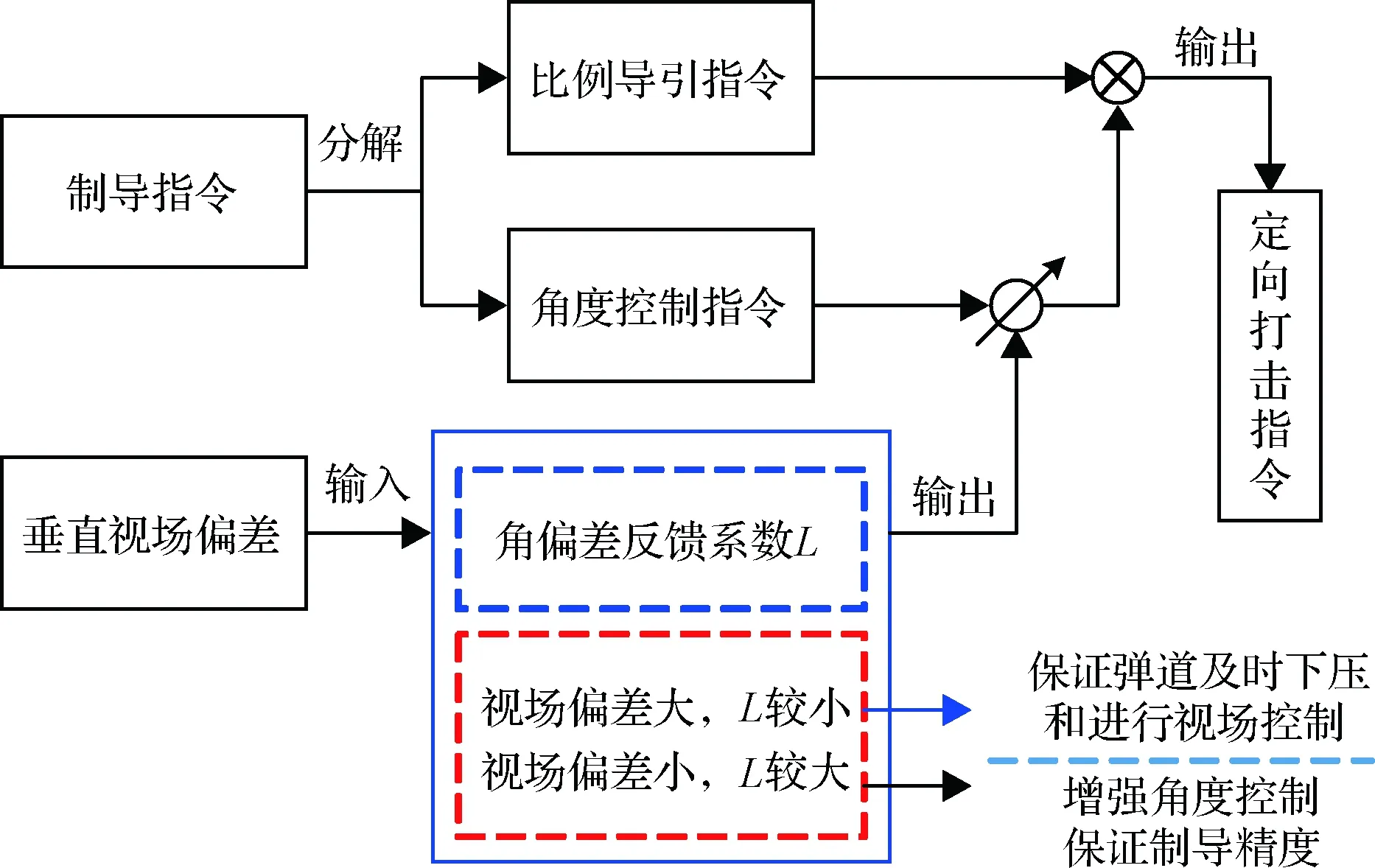
图3 定向打击制导策略Fig.3 The guidance scheme for impact angle control
1.2 末端落速控制
传统基于理想速度指令曲线的方法进行落速控制主要存在以下问题:①基于弹头垂直落向目标的假设条件,这与实际飞行相差很大,尤其是弹道拉起后,速度方向接近水平;②忽略重力的影响对带速度控制且再入飞行时间较长的机动飞行器而言引起的误差较大;③基于弹头按零攻角再入假设不合理,由于要进行减速控制,飞行器必须在大部分时间进行大攻角飞行;④需要针对特定任务和对象进行系数调节和预留速度偏差。可见,理想速度曲线的精度不足主要是由于其忽略了诸多影响速度控制的因素。速度指令的生成方法是影响减速控制精度的关键所在,这就需要建立一套较为精确的速度指令生成方法。
影响能量耗散的主要因素是阻力和弹道倾角,增大阻力(即增加攻角)和减小弹道倾角,都可以增大能量对高度的耗散效率。因而,若能够较好的估算飞行过程中的弹道倾角和攻角,则可得到相对比较精确的速度指令,并可以避免不断地进行数值积分以及寻优计算,从而极大地提高减速控制精度和节约飞行器的在线计算能力。因而,本文所采用速度指令生成方法如图4所示。将飞行器所处高度划分为N段,并预测各段的攻角和弹道倾角,然后利用机械能计算公式从终端位置开始由下向上反向叠加计算到当前位置处,得到的速度作为当前时刻的速度指令。
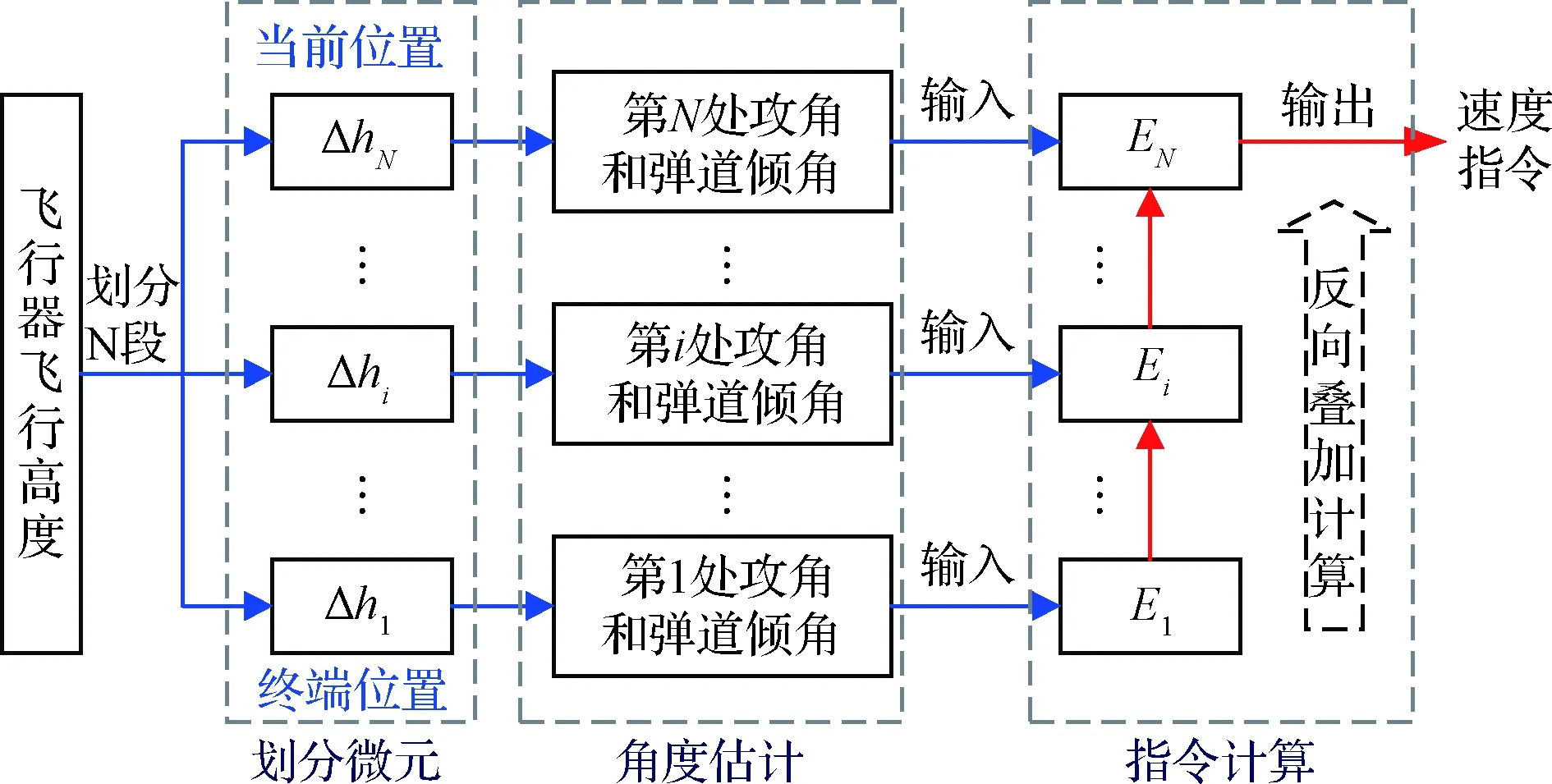
图4 速度指令生成方法Fig.4 The generation method of velocity command
2 再入滑翔定向打击制导算法
本文将再入滑翔制导过程设计为弹道调整段和末端攻击段两部分,以拉起俯冲的方式对目标进行攻击。其中,弹道调整段主要实现初步大幅度减速,并使飞行器满足中末制导的交班点条件;而末端攻击段主要配合精准减速指令完成弹道下压及实现对目标的定向打击。
2.1 弹道调整段制导算法
如图5所示,根据飞行器再入弹道的特点,首先将飞行器再入弹道划分为初始下降段,滑翔飞行段及末端攻击段。弹道调整段主要由初始下降段及滑翔飞行段组成。初始下降段的制导目的主要是为了使弹道尽快拉起并满足滑翔飞行所要求的条件;滑翔飞行段主要是跟踪所设计的在线参考轨迹,使飞行器达到减速要求以减轻末端攻击段的减速压力,并使其满足中末制导的交班条件。此外,飞行器再入过程雷达全程开机,所以要求飞行器能够对目标进行稳定跟踪。
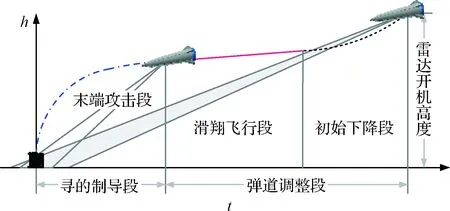
图5 高超声速滑翔飞行器再入弹道划分Fig.5 Different flight phases of the reentry trajectory
飞行器的速度和高度方程可表示为
(1)
(2)
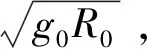
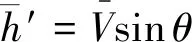
(3)
(4)
如图6,在速度—高度空间中,以当前目标点(VM,h)与期望的滑翔段终端条件(VMf,hMf)连线为参考基准,进行弹道调整段轨迹规划。
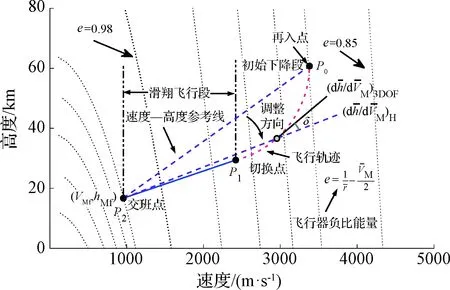
图6 速度—高度空间状态转移轨迹规划方案Fig.6 The planning scheme of the state transition trajectories
因而,在初始下降段及滑翔飞行段的弹道倾角指令为
(5)
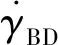
(6)
利用式(3)和(4),可以得到飞行器再入轨迹在速度—高度空间中的斜率为
(7)
参考轨迹在速度—高度空间中的斜率为
(8)
对于初始下降段,本文的主要目的是使飞行器弹道尽快拉起,而侧向制导律主要用来减小初始横程。进而,初始下降段的侧向制导律可以表示为
(9)
式中:ψ为航向角;λT为方位角。
此外,本文选用的初始下降段停止条件为
(10)
式中:δH为某一指定的正小实数。
对于滑翔飞行段,结合式(5)、(7)和(8),希望规划轨迹满足关系:
(11)
进而,可以得到跟上规划轨迹需要采用的攻角幅值为:
(12)
其中,
(13)
在滑翔飞行段,纵向平面平衡攻角较小,由式(12)所得攻角αc主要用来通过跟踪参考轨迹进行减速。进而,滑翔段的侧向制导律幅值可表示为
(14)
飞行器当前位置的横程可以写为
(15)
其中,stogo为剩余航程。考虑航向视场约束ΔΨmax后的横程边界可以表示为
(16)
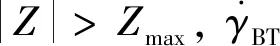
(17)
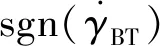
(18)
(19)
其中,λD为高低角。
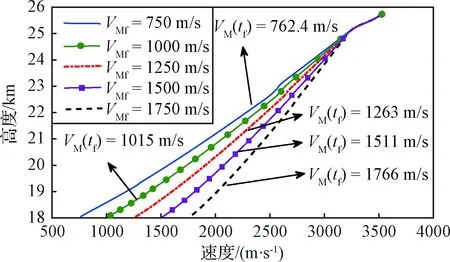
图7 不同期望速度条件下滑翔段减速效果Fig.7 Deceleration effects for different velocity constraints
图7给出了在不同减速期望速度条件下,利用以上弹道调整段制导算法所得到在速度—高度空间的减速效果图。从图7可以看出,对于以上5种情况,实际减速精度与期望速度偏差最大仅有16 m/s,展现了该制导方案具有较好的减速效果。
2.2 末端攻击段制导算法
为实现末端攻击段弹道下压并对目标进行定向打击,本文引入偏置比例导引法以协调比例导引指令与角度控制指令之间的关系。偏置比例导引方法形式如式(20)所示:
(20)
式中:N为导引系数,b为偏置项。对式(20)从当前时刻t到终端时刻tf进行积分,可得
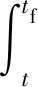
(21)
式中:γD,f为末端所要求的速度倾角;λD,f为末端高低角。在终端时刻t→tf,一般有γD,f+λD,f=0。对式(21)进行整理可以得到角偏差B(t)为
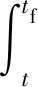
(22)
对于τ∈(t,tf)时,取b(τ)=b(t),那么由式(22)可以得到任意时刻偏置项为b(t)=B(t)/tgo。为加快角偏差收敛,可在B(t)前乘以参数L,则式(20)可以进一步表示为
(23)
将B对时间求导,并将式(23)代入可得
(24)
可见,当L>1时,初始角偏差及其变化率会随着时间的推移而逐渐收敛到零。在本文中,利用Lyapunov方法将其值取为
L=p(N-1)
(25)
式中:p∈(0, 1)。
为便于分析,将式(20)分为比例和偏置项两部分,分别表示为
(26)
(27)
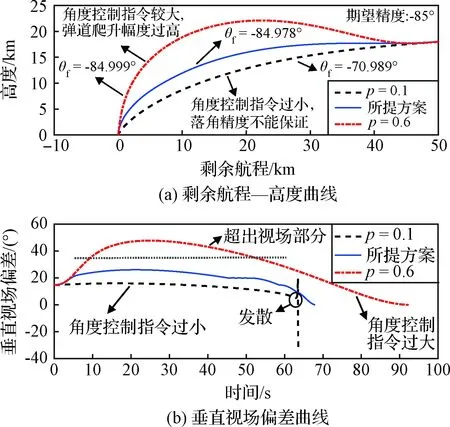
图8 参数p对末端攻击段弹道的影响示意图Fig.8 Effects of p on the terminal guidance trajectory
综合以上分析,本文可将p作为一个惩罚函数,即在弹道前段,将p取为一较小值,以保证弹道快速下压。在弹道中末段,可将p值逐渐增大,以保证角偏差B尽快收敛到零。弹道的爬升幅度可以通过垂直视场偏差ε=|λD+θ|进行衡量:ε越大,弹道爬升越大;ε越小,弹道爬升幅度越小。采用传统的割线法,参数p可根据ε取为如下形式:
(28)
式中:δmax和δmin分别为参数p所设定的最大和最小取值,满足0<δmin<δmax<1;εu和εl分别为所设定的垂直视场偏差上下限值。通过抑制弹道爬升也可使保证导引头对目标的稳定跟踪。
3 末端精准减速控制算法
3.1 减速控制方案
要保证导引头能够正常工作就必须对飞行器进行减速控制,因此高超声速滑翔飞行器再入过程对落速的大小和方向均有一定的限制。文中2.2节给出的导引规律尽管可以实现对速度方向的控制,但无法实现对速度大小的控制。飞行器只能靠增加攻角来增加阻力才能减速,而增加攻角又要尽量避免改变导引攻角的大小和方向,因此本文选择在导引攻角αg垂直方向增加一个附加攻角αN,通过在导引弹道基础上做锥形运动进行减速,如图9所示。
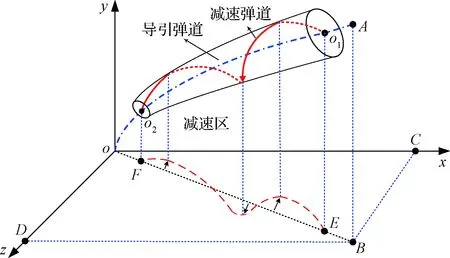
图9 导引弹道与减速弹道对比示意图Fig.9 The diagrammatic map of the guided and deceleration trajectories
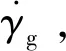
(29)
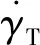
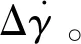
(30)
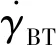
(31)
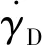
(32)
根据文献[16],附加攻角αN的计算公式为
(33)
式中:κ为一修正系数;Vc为所要设计的速度指令。由于在接近目标时,考虑到控制系统的限制,侧向机动幅度过大会造成弹道无法及时收敛,进而造成脱靶。因此,本文将最大附加攻角设计为图10所示剖面,以确保飞行器可有足够的减速高度及保证弹道及时收敛。由式(33)可以看出,速度指令Vc的精确程度直接影响减速控制的效果。
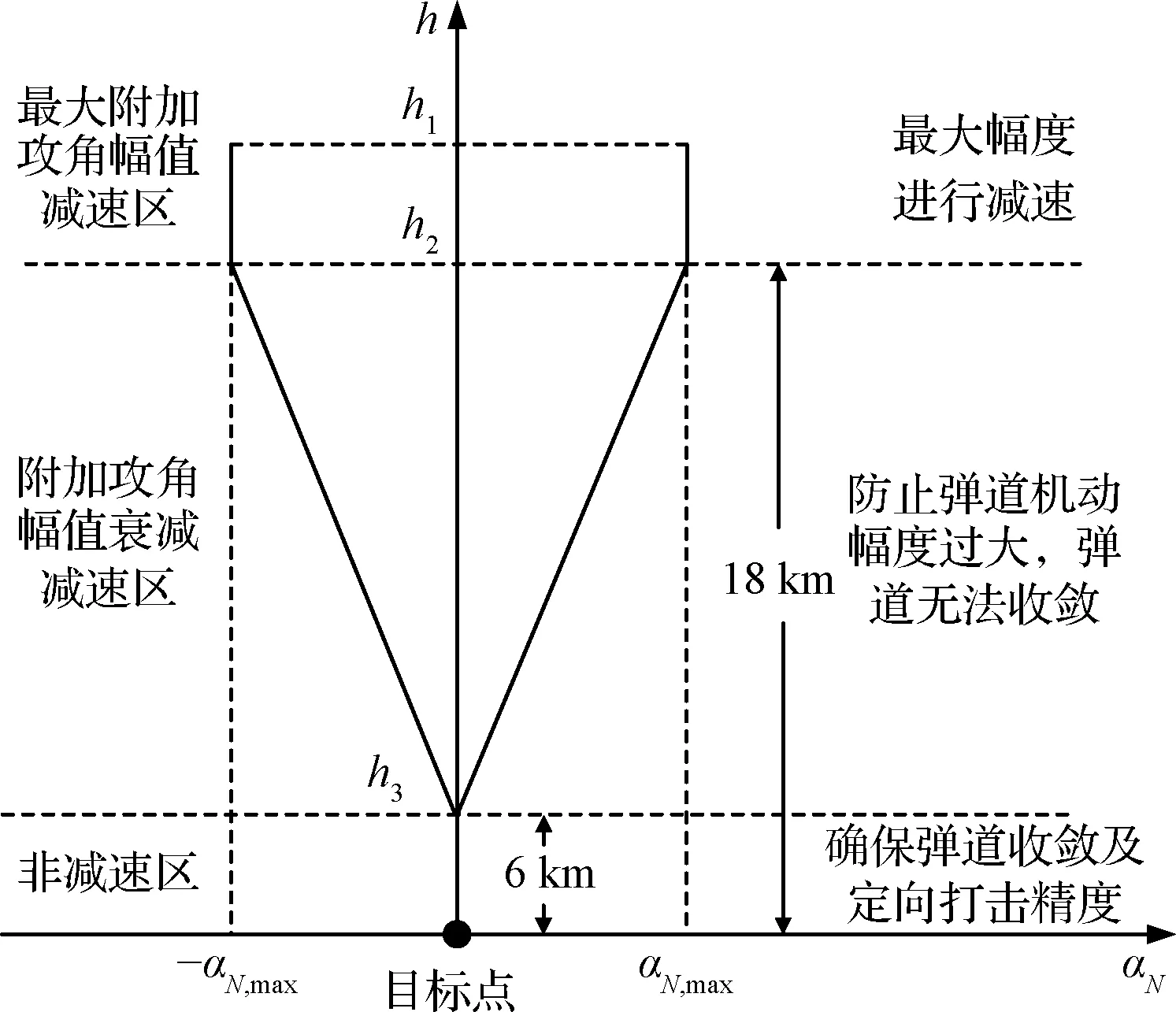
图10 最大附加攻角幅值设计剖面Fig.10 The maximum additional angle of attack design profile
3.2 攻角和弹道倾角的在线估计
本节在所设计的偏置比例制导算法的基础上,对α和θ进行合理估计。定义ηD=γD+λD为前置角,并将ηD对时间求导可得
(34)
近似认为r/VM≈tgo,并将式(34)除以式(24),可得
(35)
将式(35)积分后,可得
(36)
其中,
(37)
同理可得λD的表示为
(38)
其中,
(39)
考虑到γD=ηD-λD,γD可表示为
(40)
侧向对准后,一般满足关系λT-ψ=π。进而,对式(40)求导后,代入式(18)中可得
(41)
(42)
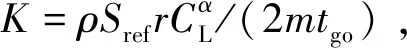
(43)
此外,对式(41)进行积分,可得
(44)
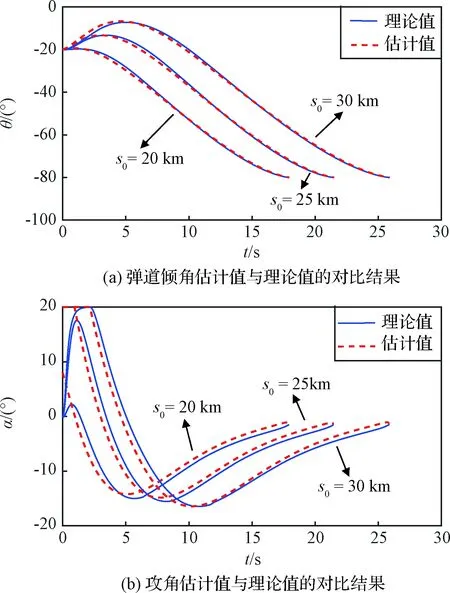
图11 估计值与理论值对比结果Fig.11 Comparison results between estimated and theoretical values
式(43)和(44)的估计精度依赖于剩余时间tgo,而剩余时间的估计精度又依赖于相对距离r的精度。由于r的幅值较大,较小的角度偏差都会造成较大幅度的距离估计误差。为补偿误差,可使r的使用值收敛速度稍快于理论值,以加速α和θ估计值的收敛。图11为初始高度为20 km,不同初始航程条件下,通过补偿后θ和α估计值与理论值之间的对比结果曲线。可以看出,通过补偿,θ和α的估计精度是比较高的。
3.3 减速指令的生成
依然采用指数密度形式,将式(1)与式(2)相除,整理后可得飞行器机械能对高度的导数为
(45)
应用微元迭代的思想,将高度—能量曲线分为N段,每一段为一个能量元,当N足够大,总能量可表示为
(46)
式中:E0为飞行器击中目标且满足落角和落速约束时的机械能。将能量顺着高度增加的方向积分到飞行器当前位置,ΔEi为其中第i段能量元,根据式(46),ΔEi可表示为
(47)
式中:θi,CD,i和VM,i为第i个能量微元上飞行器的弹道倾角、阻力系数和速度;Δhi为第i段高度微元。当划分足够小,可以认为每一段上的弹道倾角和阻力是恒定不变的,从而得能量推演方程
(48)
式中:Δhk≈Δrkcos(π/2+θk)。攻角和弹道倾角可通过式(43)和(44)获得。已知hi处能量为Ei,则hi处的对应速度大小应为
(49)
进而,可以得到飞行高度处的速度VM,N。令速度指令为Vc=VM,N,便可由式(33)得到附加攻角。进而,可由式(31)得到加入减速控制后两个方向上的制导指令。
4 仿真校验
为检验本文所设计再入滑翔制导算法的性能,在给定初始条件(见表1)和约束条件(见表2)下对制导算法性能进行了仿真校验。导引系数在弹道调整段取值为1,在末端攻击段取值为4。为保证末端制导控制系统的稳定,防止各个制导指令(比例、角度控制及减速指令)之间的相互干扰,当飞行器所处高度小于6 km时,停止减速控制,以保证其脱靶量和落角约束的控制精度。
4.1 落速控制及性能对比
为验证所提制导方案的弹道特点及制导效果,

表1 初始基准值Table 1 initial conditions

表2 再入约束条件Table 2 Constraint conditions
将落速和落角约束分别取为600 m/s和-85°,再入初始速度取为4500 m/s,进行了数值仿真,并由图12给出了相应的仿真结果。
从图12(a)可以看出,飞行器通过类似一个“C”形弹道来实现对目标的定向定速打击。在满足热流和动压要求条件下,滑翔段终点与期望速度之间偏差只有13 m/s,落速和落角偏差分别只有4 m/s和0.8°(图12(b)和(c))。从图12(d)和(e)中可以看出,垂直视场偏差在下压机动时幅度最大,侧向视场偏差在倾侧反转时最大,但均满足视场偏差要求(在35°以内)。图12(f)、(g)和(h)给出了相应的过载曲线和攻角曲线,均满足表2给出的过程约束条件。
表3分别给出了在不进行减速(用1表示)、打击静止目标(用2表示)以及速度为20 m/s的运动目标(用3表示)时的统计结果。可以看出,所设计制导方案减速效果极为明显。对于运动目标,其落速和落角控制精度均有所下降,但由于所打击的目标速度相对极小,其影响幅度十分有限。
为校验本文所提末制导方案的制导性能,特将其与潘兴II理想速度曲线减速制导方案在不同落速约束条件下对脱靶量进行统计分析和对比,仿真统计结果见表4和表5所示。
从统计结果可以看出,两种制导方案均能够保证飞行器命中目标,且均具有较高的落角控制精度。然而,改进理想速度曲线需要针对特定任务进行系数调节及预留速度偏差,在落速要求为700 m/s和500 m/s时,采用改进理想速度曲线方案的落速偏差较大,其幅度甚至达到了近100 m/s左右。而本文所提制导方案,在以上各种情况下均具有较高的落速控制精度。
4.2 制导算法的鲁棒性验证
为验证制导算法的鲁棒性,本文在标称条件的基础上对各变量进行拉偏(见表6),并随机选取1000组极限偏差组合进行仿真校验。落速、落角及脱靶量的统计结果如图13所示,其中☆代表不满足
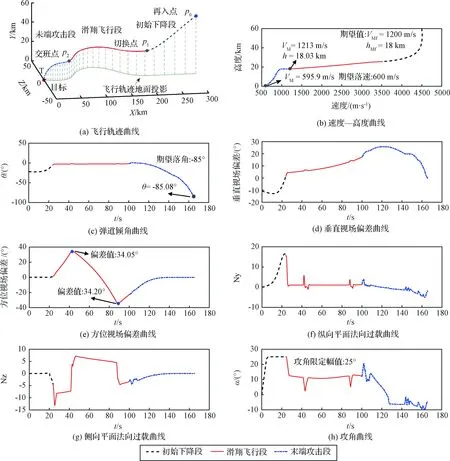
图12 所提制导方案的制导效果Fig.12 Simulation results for the proposed guidance scheme
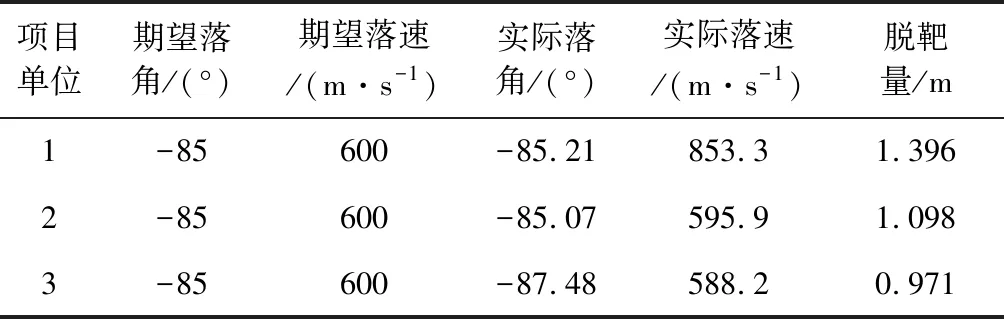
表3 不同制导目的条件下的仿真结果统计Table 3 Statistical results for different guidance purposes
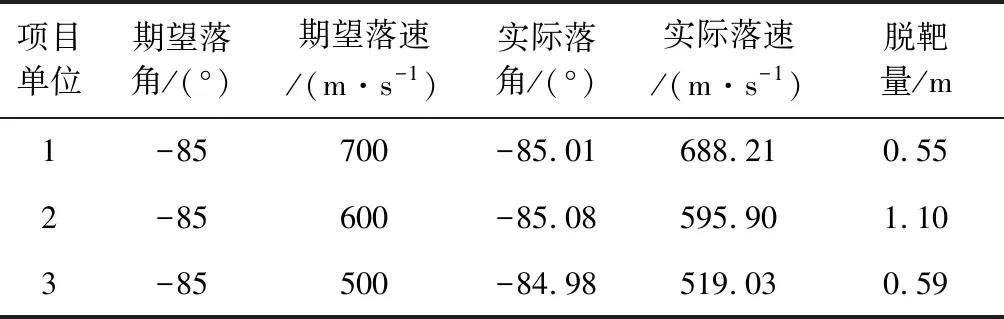
表4 本文设计制导方案仿真结果统计Table 4 Statistical results for the proposed guidance scheme
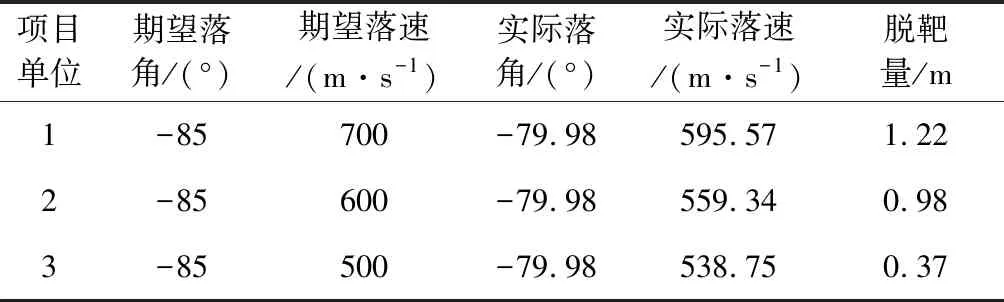
表5 潘兴II基于理想速度曲线制导方案仿真结果统计Table 5 Statistical results for the Pershing II guidance law

表6 各变量拉偏幅度Table 6 Deviation values
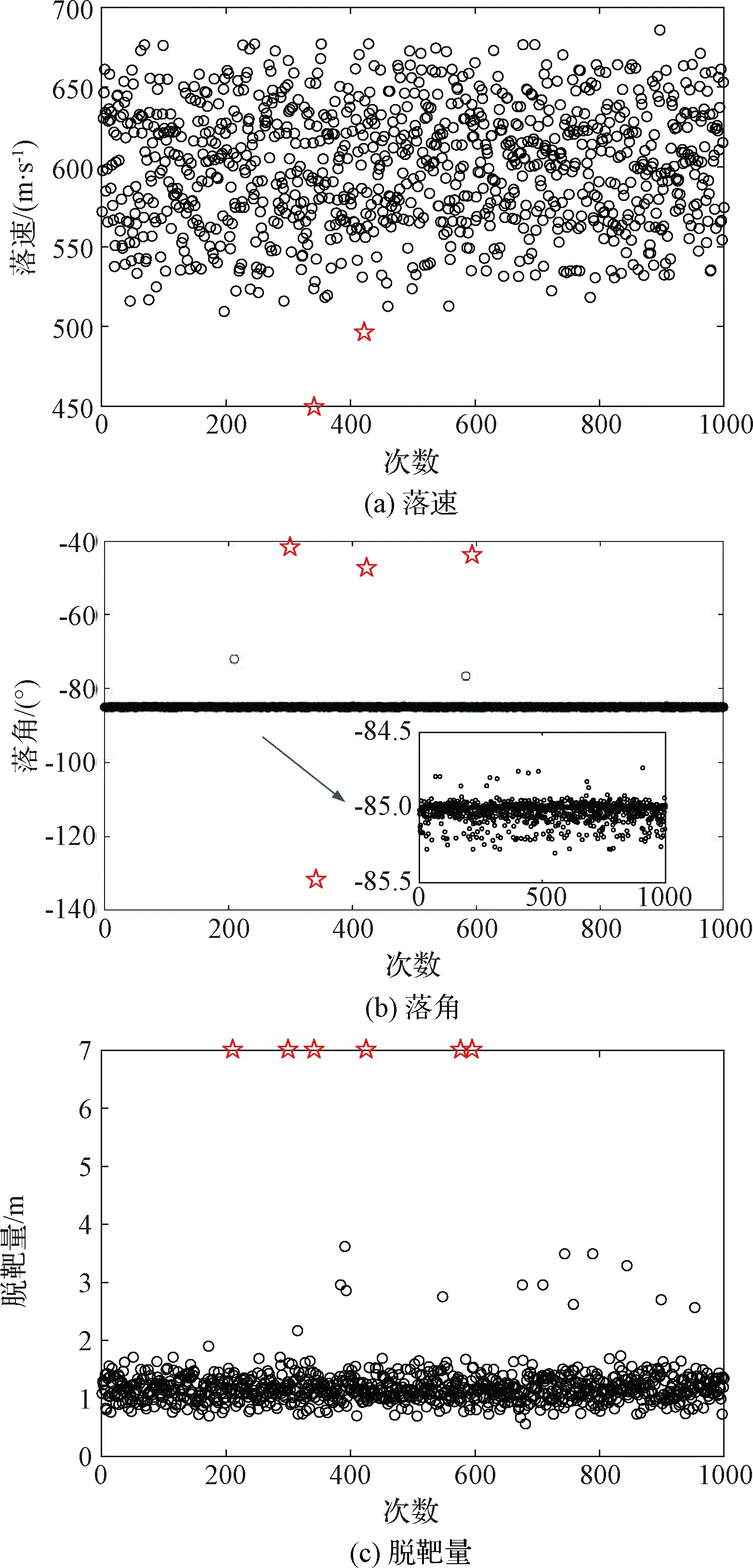
图13 1000次极限偏差组合统计结果Fig.13 Statistical results of 1000 fire tests
要求的结果(脱靶量大于7 m按7 m记录)。
从统计结果可以看出,对于这1000次极限拉偏组合情况,只有6种情况不能满足性能指标要求。统计结果表明了该制导方案针对初始偏差、气动及密度偏差均具有较强的鲁棒性。
5 结 论
1)采用本所提制导方案,在考虑多种过程约束条件下,可在较短的滑翔距离内实现落速、落角控制且满足脱靶量要求,并具有较强的鲁棒性。
2)通过引入弹道调整段和变角偏差反馈系数偏置比例制导算法,可使飞行器具有较为宽松的再入初始条件、减速控制能力及良好的弹道下压能力,并具有较高的落角控制精度。
3)相比于理想速度指令生成方法,本文所提出的基于攻角和弹道倾角估计高度修正速度指令生成方法,所建模型精度高,不需要针对特定任务进行系数调节和预留速度偏差,具有较高的减速精度。由于减速控制使导弹进行的锥形机动,也极为有利于高超声速滑翔再入飞行器的末端突防。
