为“思”而学

张宏伟

全景式数学教育倡导：始终关注并充分发掘每一项数学内容、每一次数学教学活动在培养数学思考方面的重要价值，让学生用数学学会思考，更多地为学生的思维发展而教，更多地为学生“成为有思想的人”而教，更大程度上把“数学知识的教学”转变为“数学智慧的教育”。

下面以长方形和正方形的周长为例，说明全景式数学教育，如何用一节看似简单、貌似没有多大思维含量的课，来发展孩子数学思维、培养孩子数学智慧。

一、一样的学习内容

以北京版小学数学教科书三年级上册，第70、71页，例2、例3（分别见图1、图2）为例。

二、不一样的学习目标

1.知识技能：理解、掌握长方形和正方形的周长计算公式，会计算长方形、正方形的周长。

2.问题解决：能正确判断和抽象哪些生活问题是求哪样的图形的周长问题，能解决生活中相应的、简单的实际问题。

3.数学思考（上位与核心）：

①在思考周长问题时，能根据周长的意义，进行相应的空间想象，自觉向物体或图形一周的边线定向。明确求周长的时候，应该把思考的着力点放在分析边线的特征上。

②能自觉地根据特征进行分类思考，决定采用一般的方法，还是与特征匹配的特殊方法。感悟到一般问题用一般方法去解决，特殊问题用特殊方法去解决;感悟到一般性方法是通用的方法，特殊的方法只能解决具有同样特征的专项问题。特殊问题用特殊方法解决会更简便。

③感悟用特殊方法解决问题的核心是发现事物和图形的特殊之处;从不同的角度来思考，可以发现不同的特殊性，继而发现不同的特殊方法。

④通过汇总、比较、分类、类推等策略，对同类问题进行整体性分析和思考，初步学会系统、结构性地思考和解决问题。

4.情感态度：在发现与周长问题相关的一般和特殊规律的过程中感受数学的简洁、概括、神奇之美，在丰富多彩的学习过程中感受数学学习的有趣和快乐，在处理和解决问题中感受研究数学的价值。

三、不一样的推进逻辑

这部分内容，国内所有版本的教材编排的思路都是先学长方形的周长，后学正方形的周长，无一例外。笔者却把它们颠倒了过来，先学（图2）正方形的面积，再学（图1）长方形的面积

笔者之这样颠倒，正是因为笔者看到了它培养孩子思考力的特殊价值。

笔者把这节课的推进逻辑（思考逻辑）确定为

先两头后中间！也就是先研究“一种极端情况”，再研究“相反的另一种极端状况”一最后研究“中间状况”。

四、不一样的课程设计和教学过程

推进逻辑确定后，笔者以四点数学思考目标为核心进行了课程和教学的重建，具体的学习过程大致分为六个环节进行。

环节一：笔者引导学生把生活问题抽象成数学问题。

出示学生生活中的实际问题和情境，引导学生通过自己的思考、辨析和讨论，明确求篱笆、封条、边框、围池塘走一周的长度等生活问题（见图3），就是求相应图形边线的总长，即“周长”。

环节二：依次出现下面图形.让学生列算式求周长。

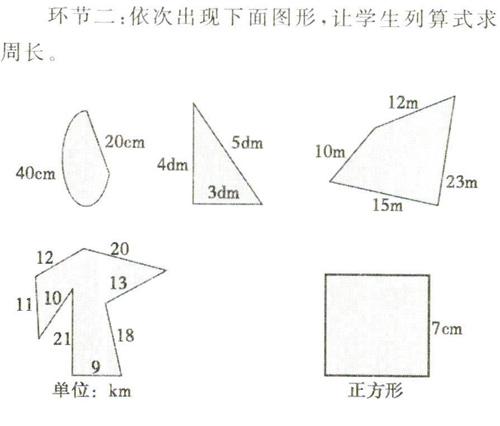
正方形的前四个图形，学生都是用连加法，当正方形出现后，学生自然出现两种算法，而且认为用乘法更简便。

笔者接着追问，引发学生进一步思考：乘法简便，前面的为什么不用，只有它用？

生：因为它特殊，四条边都一样。

师：它特殊，用特殊的方法（乘法）去解决，那这些一般的呢？

生：用一般的方法去解决。

此时，学生的智慧火花已经开始闪观。

环节三：跳出正方形

1.我先拋出这两个图形：

师：它们能用特殊办法解决吗？

生：能，因为它们也是特殊的，四条边都一样？

通过这两个图形，让学生突破了直角和直边的限制。

2.再推广到正多边形：

通过让学生解释省略号的意思，启发学生概括出：正几边形，就用边长×几。

3.再引入五角星突破凸平面圖形的限制：

4.最后，集中起来，整体比较，系统分析：

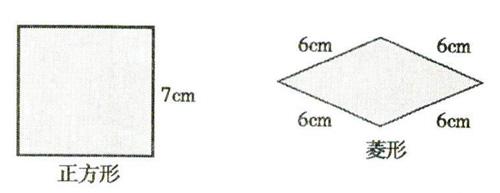
学生就会发现：求图形的周长，不管曲直、凹凸，只要所有的边长相同，就直接乘法计算：边长×边数。这是一种整体的、系统化、结构性的思考训练。

老师们，回忆上面的过程，笔者仅仅是在教正方形的周长吗？

绝对不是！

正方形只是思考特殊图形周长的一个跳板，是发现“特殊问题特殊解决”的敲门砖。

环节四：从长方形周长学起

在学生研究完“最特殊”的正方形的基础上，进入第4个学习模块——研究长方形的周长：

师：你觉得它特殊吗？

生：有一点特殊，特殊的地方是两个长一样，两个宽一样—所以用：长×2+宽×2。

生：可以看成最特殊的：这半圈的长和宽联合起来，和那半圈是一样的。所以，可以先求出半圈，再乘以2。

这种算法很难理解的，它是本节课的难点。这时，笔者把数学戏剧拉了进来。

这是一组学生在排练长和宽的过家家：他们把红色的长比喻成男的，黄色的宽比喻成女的，然后一个长和一个宽结婚成一家人，这样就可以组成两个家庭，这两家的总长完全相同，所以用长加宽的和乘以2。形象、生动、有趣，好理解，有学生一辈子都小会忘。

接着再引入下面四种图形让学生求它们的周长：

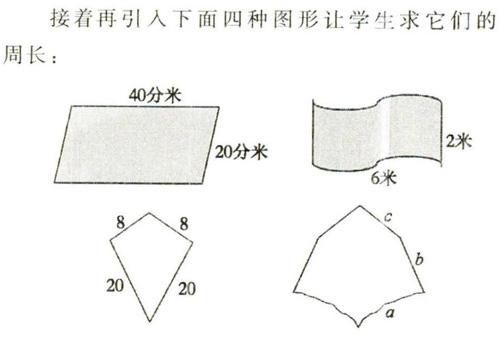
从直线到曲线，从直角到任意角，从四边到多边，让学生学会类推，学生的思维一下子又打开了。

最后一个图形，还引发了一段很逗趣的一段话：有的学生说像正方形一样过家家，右边的a、6、c三个人（边）是一家，左边的三个也是一家，两家的总长度是一样的，所以先用a+b+c，然后再乘以2。有的学生立马反对，三个人怎么能结婚呢？有的学生马上回击：这不是玩游戏吗？让人忍俊不禁。

老师们，发现没？长方形也只是解决这类问题的一块敲门砖！

环节五：补上中间，全景分析

1.补上中间：

任何事物都不是非黑即白，还有中间的灰色地带。

在学生研究好上述图形周长后，还又全景地完善图形类型和思考区域——补上图形的中间地带：

笔者首先引导学生认识到所有边“都不一样”和“都一样”是两个相反的极端，那么，下面四个图形，学生自然就把它们放在中间地带。

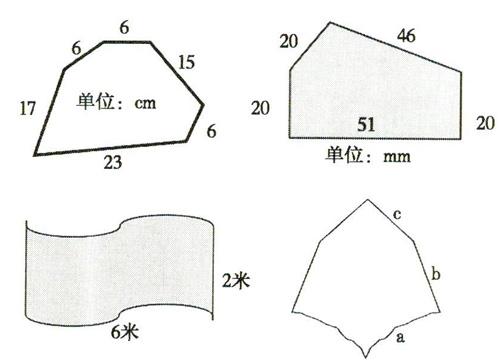
2.全景分析

最后，把本节课研究过的图形，汇总成下图：

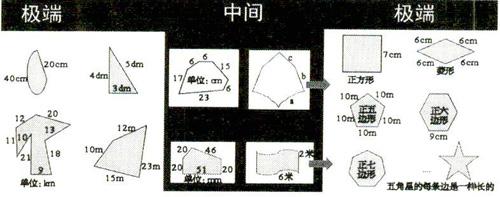
让学生看着汇总的全部图形，同顾本节课的研究经历，随便聊聊自己的看法、自己的想法。学生谈到的想法有：

l.左边都不一样长，只能用一般方法，也就是加法解决。右边都一样长，是特殊的情况，用特殊方法，也就是乘法解决。中间也可以用乘加解决。

2.加法可以算所有图形的周长，乘法只能算特殊的、边都一样的图形。

3.特殊的图形用特殊方法更简便。

4.求周长要注意看它的边是不是都一样长。

5.有的中间图形，把边联合起来看，可以变成都是一样的图形（此时，我点破：这样就把中间的图形，变成了最特殊的都一样的图形，这就叫转化）。

6.我们先学了极端的，后学习了中间的等等。

环节六：超越数学

师：孩子们，不仅仅是数学上的问题，生活当中遇任何问题，你都要先分析是什么情况。一般的情况一般对待，用一般的方法解决;特殊的情况应特殊对待，用特殊的方法解决。

比如，按照我们班级的约定，迟到是该批评的。如果迟到的学生在上学的路上，因为帮助路人，迟到了几分钟，你说觉得该批评吗？

学生都觉得不应该批评，应该表扬。教师点拨：这就叫特殊情况特殊对待——这是在毓养更一般的、通用的思考方式和处事态度。