液体火箭发动机金属软管网套承载特性研究
2019-07-03武晓欣秦红强
赵 剑,武晓欣,秦红强,马 键
(1.西安航天动力研究所,陕西 西安 710100;2.液体火箭发动机技术重点实验室,陕西 西安 710100)
0 引言
现代液体运载火箭通常采用摇摆发动机调整飞行姿态[1],发动机摇摆运动过程中,金属软管作为柔性关节连接管路固定部分与摆动部分[2],以补偿摇摆运动产生的变形和位移,维持推进剂连续供应和发动机正常、可靠地工作。因此,柔性金属软管的结构特性直接影响发动机的可靠性[3]。
金属软管一般由波纹管、铠装环以及编织网套等组成[4],长期以来,工程上对金属软管的研究多集中在波纹管部分[5-10],而对网套结构研究较少。网套包覆在波纹管外表面,相当于增加了波纹管壁厚,可增强波纹管的承压能力[11]。文献[12]研究表明,不同编织角度的网套对金属软管整体承压能力和轴向刚度影响较大,对弯曲变形能力影响较小。在扭转变形时,网套限制了波纹管的横向变形,能大幅提高金属软管的抗扭能力和抗失稳能力[13]。
网套多为金属带缠绕而成,结构复杂,其变形过程中,金属带之间相互接触、挤压,非线性特征显著,仿真难度大,因而大多数研究工作都基于简化的网套模型,研究结果量化程度不高。对网套本身结构特性的研究还不足以说明网套对金属软管的增强模式和增强机理,难以得到适用于工程应用的有效指南。鉴于此,需要综合研究波纹管、铠装环和网套整体的结构特性。为了使分析方法更具工程实用价值,本文提出了网套参数化建模思路,基于APDL语言实现了网套建模以及非线性有限元分析的程序化,开展了相关试验证实了模型及分析方法合理可行;研究了承压状态下网套对金属软管的增强机理及相互作用模式,给出了基于有限元解定量评估网套增强能力以及校核网套强度的方法。
1 网套结构与参数化建模
1.1 网套结构
金属软管的结构组成如图1所示,铠装环与波纹管紧密贴合,支撑并加强波纹管;网套包覆在铠装环外表面,保护内部结构。在非工作状态下,网套与内部结构之间存在接触挤压作用。
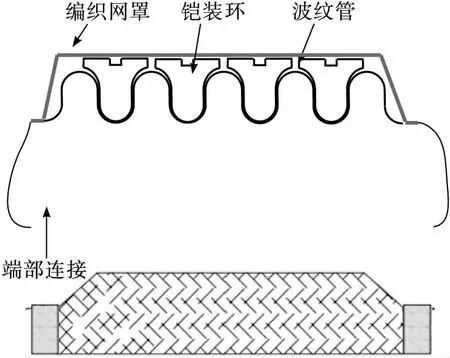
图1 金属软管示意图Fig.1 Schematic diagram of flexible metal tube
网套由若干股金属带按一定顺序和夹角沿着波纹管母线相互交叉编织而成,其交叉螺旋结构可等效为金属软管外圆周上任意点绕中心轴线做等速旋转运动的同时,沿中心线做等速移动而形成的轨迹,即网套中任意金属带的形状均为圆柱形螺旋线,其特征方程为
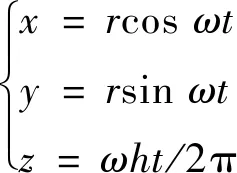
(1)
式中:ω为角速度;h为螺距;r为螺纹半径;t为控制参数。
1.2 参数化建模
网套中金属带形状一致,呈周期性均匀编织在金属软管外圆柱面内,结构复杂,如图2所示。

图2 网套局部结构图Fig.2 Local diagram of meshy hose
基于该特点,网套参数化建模思想为:以网套圆柱面底部任意点为基点,首先按相反螺旋方向生成两股交叉螺旋带,然后将其沿着圆柱面底圆均匀复制,即可生成网套三维有限元模型。网套螺旋线特征方程见式(1),网套结构由螺纹半径、螺距以及金属带股数决定。基于参数化建模思想,采用ANSYS的APDL语言,编写了网套参数化建模程序,通过调整结构参数,可快速生成所需的网套模型如图3所示。
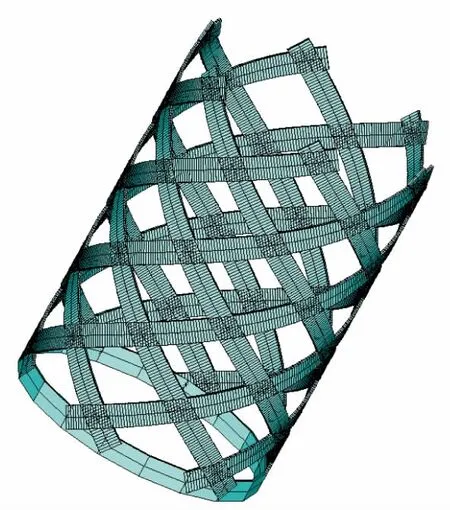
图3 有限元模型示意图Fig.3 Schematic diagram of FEM model
2 数值计算方法与验证
2.1 非线性有限元方法
网套由不锈钢金属带交叉编织而成,其拉伸变形呈现三类特征:变形量远大于最小特征尺寸(厚度),金属带之间接触作用复杂,可能产生弹塑性变形。因此,网套结构特性的有限元求解耦合了几何非线性、接触非线性以及材料非线性因素。
考虑到几何非线性影响,采用ANSYS分析时,需设置大变形模式,并减小载荷梯度增量。有限元模型选用矩形截面梁单元BEAM189[12],通过合理控制节点位置,耦合螺旋线相交节点的平动自由度,释放法向转动自由度来模拟网套交叉叠加的情况。材料非线性表现为弹塑性本构模型,基于Von-Mises屈服准则,假设材料具有各向同性硬化特质,定义幂指数硬化模型描述材料进入塑性阶段的本构关系。引入Mises等效应力作为硬化参数
(2)
式中J2σ为应力偏量的第二不变量。
基于ANSYS的APDL语言,结合上述分析方法,编写了完整的网套非线性有限元分析参数化程序,包括建模、网格生成、接触处理、加载以及求解设置等步骤。通过调整网套几何参数和载荷大小,可以进行任意结构网套的有限元分析,极大地提高了效率,节省了时间。
2.2 试验验证
为了验证建模和分析方法的正确性,针对某典型网套进行了轴向拉伸试验。试验装置如图4所示,网套上端固定,在自然垂直的情况下,分别在下端施加6组递增的载荷,记录网套下端的轴向位移,整理出伸长率数据,作为非线性有限元分析的验证依据。

图4 网套轴向拉伸试验装置Fig.4 The axial tensile test apparatus
采用有限元方法对试验进行仿真分析,其中网套材料为1Cr18Ni9Ti,弹性模量E=184 GPa,泊松比v=0.3,屈服极限205 MPa。将网套一端节点固支,在另一端施加轴向载荷,计算网套端部节点的伸长率。轴向位移和径向位移响应如图5所示,网套轴向拉伸时,沿长度方向轴向变形均匀;由于网套端部自由度耦合模拟法兰连接情况,拉伸状态下,网套中部出现类似“颈缩”现象,与试验现象一致。试验与有限元计算结果对比如图6所示,可以发现,不同载荷下有限元解与试验结果基本一致,最大误差3.6%,证实了模型以及耦合节点的处理方法正确。
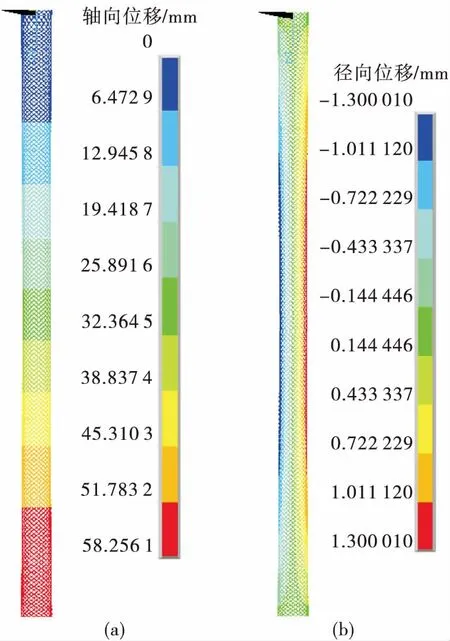
图5 网套位移分布Fig.5 The displacements of meshy hose
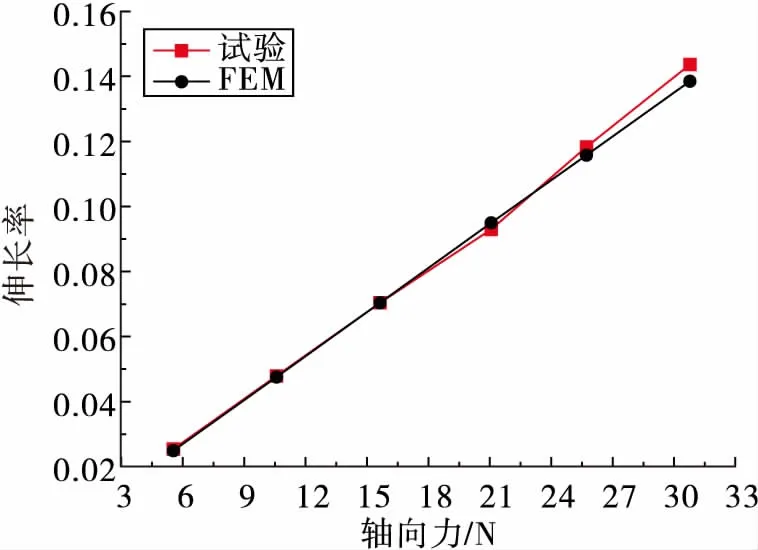
图6 试验验与有限元结果比较Fig.6 Comparison of experimental and FEM results
3 网套结构特性
内压作用下波纹管径向膨胀使铠装环与网套接触作用增强,由于整体结构、载荷以及变形周期性对称,故采用三维周期性模型进行分析。考虑到波纹管、铠装环以及网套之间接触作用复杂,三维计算网格和存储成本太高,因此仅采用非线性有限元方法研究承压特性,在此基础上理论推导,分析网套的增强作用和变形补偿特性。
3.1 网套承压特性
整体周期性有限元模型如图7所示,波纹管与铠装环间建立“面-面”接触关系,网套与铠装环之间根据接触关系,建立位移约束方程,耦合节点位移。金属软管两端固支,波纹管内表面施加10 MPa内压载荷。
取出部分网套的周向应力和径向位移结果如图8所示。由于径向接触挤压,网套受力和变形不均匀,与铠装环接触部分周向应力和径向位移都相对较大,但整个网套材料处于弹性变形状态,具备一定的承载余量。
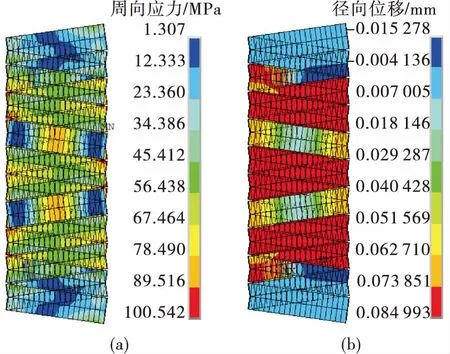
图8 内压载荷响应Fig.8 The structural responses of internal pressure
3.2 网套增强作用
金属软管承受内压时,波纹管与铠装环径向膨胀变形挤压网套,导致螺旋金属带处于“绷紧”状态,其变形可等效为网套承受均布内压pw的效果。pw的值表征网套分担内压载荷的大小,也代表网套对整体承压性能的增强能力。将网套视为圆柱壳,半径记为Rw,在内压作用下,假定网套径向均匀膨胀ΔR,取一部分结构(两层叠加,见图9)。

图9 螺旋交叉叠加网套结构示意图Fig.9 Schematic diagram of helix across structure of meshy hose
当网套径向变形ΔR时,金属带的周向变形2πΔR与周向张力Fz有如下关系
(3)
式中A为单根金属带横截面积。
在承受内压pw时,取任意一段网套金属带为研究对象,其周向张力
Fz=pwRwH
(4)
式中H为金属带宽度。
由式(3)与式(4)可以得到等效应力
(5)
式中b为金属带厚度。
同时,金属带的周向张应力
(6)
圆柱壳承受内压的强度条件为[4]
Swz≤(0.6~0.9)σ0.2
(7)
图8(b)表明,内压作用下网套最大径向位移0.085 mm,可得到等效压力pw=2.042 MPa,即相当于网套承受了2.042 MPa的内压作用,分担了约20%的内压载荷。式(5)表明:网套金属带越厚、径向变形越大,等效压力越大,增强作用越明显。
由式(6)可得到周向应力为Swz=93.4 MPa,与有限元极值解(图8(a))Swz=100.5 MPa吻合较好,证实了以上理论分析方法合理,且周向应力满足式(7)给定的强度要求。根据极限情况分析,当网套周向应力为0.9倍屈服极限时,对应的最大径向位移为0.17 mm,最大等效压力为4.084 MPa,即在满足强度要求的前提下,网套可分担的最大内压载荷为4.084 MPa。
3.3 网套变形补偿特性
内压作用导致铠装环与网套接触挤压,轴向拉伸时,接触面有相对滑移趋势,由此产生附加静摩擦阻力,影响金属软管的变形补偿特性。将铠装环与网套的接触作用关系简化为图10所示的圆柱坐标系,铠装环与网套接触面位于半径Rw处,铠装环根部与网套金属带局部接触。
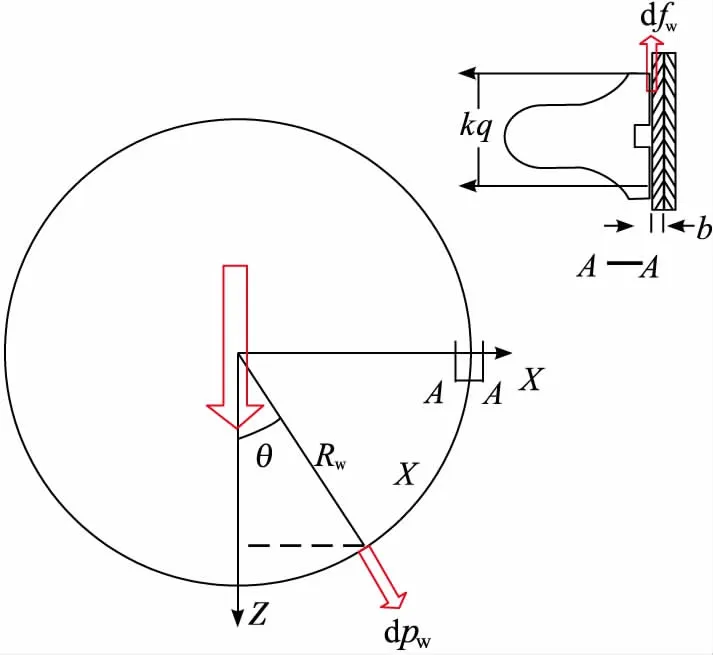
图10 网套接触作用示意图Fig.10 Schematic diagram of contact effects of meshy hose
如图10所示,在圆周θ处取弧元ds=Rwdθ,假定沿子午向长度为fL的接触面静摩擦系数为fv,则局部弧元段的摩擦力为
dfws=fvpwfLds=fvpwfLRwdθ
(8)
积分可得接触面长度为fL时,整个圆周长度的总摩擦力为
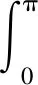
(9)
将式(5)代入式(8),可得
(10)
式(10)表明,附加轴向摩擦力随着网套金属带厚度、接触面积以及径向位移的增大而增加。对于本文研究的金属软管,当静摩擦系数fv=0.15时,在径向位移为0.085 mm的情况下,整体轴向静摩擦阻力为52 820 N,即在内压作用下,补偿轴向拉伸变形需要额外提供超过50 kN的轴向力来克服摩擦阻力。
尽管补偿等量轴向变形需要的轴向力有所增加,但并不意味着金属软管整体刚度将显著增大。因为,一方面在理想情况下,摩擦力只是将轴向力“等量”增大,而不是“等比例”放大,所以摩擦力不改变拉伸过程中“力-位移”曲线的斜率,即轴向刚度不变;另一方面,网套本身结构类似于多股弹簧并联,轴向刚度相对较小,对整体刚度影响并不显著。
4 结论
本文研究了液氧煤油发动机金属软管铠装网套的结构特性,提出了基于有限元解定量评估网套增强能力以及校核网套强度的理论分析方法,获得了以下结论:
1)网套特征几何形状为交叉螺旋线结构,采用APDL语言将网套非线性有限元分析过程参数化,并通过相关试验证实了模型及分析方法合理可行;在有限分析中,通过释放网套螺旋线交叉节点的转动自由度,可以合理模拟网套的拉伸变形。
2)金属软管承受10 MPa内压时,波纹管径向膨胀导致铠装接触挤压网套,网套分担了20%的内压载荷;在满足强度要求的前提下,网套可分担4 MPa左右的内压载荷,能有效增强波纹管的承压能力。
3)内压作用时,径向接触作用使铠装环与网套之间产生附加的轴向摩擦阻力超过50 kN,将增大金属软管变形所需力和力矩,增加伺服机构负担。
