汽轮机转子冷态启动过程的疲劳损伤分析

(江苏科技大学 能源与动力工程学院，江苏 镇江 212000)

汽轮机转子运行在高温高压的环境中，易发生疲劳损伤，其疲劳寿命决定着发电设备的使用寿命。我国汽轮机组的使用寿命年限为30年[1]，有学者认为合理评估机组的寿命和精确地修复易损部位，可以让发电设备寿命延长10～20年[2-3]。已有研究在建模过程中将转子模型简化为二维模型，但无法精准模拟汽轮机转子在实际工况下的应力状态[4-6]，通过对某135 MW汽轮机高压转子三维建模，精确模拟汽轮机转子真实运行状况下的受力状况，使计算结果更加精确，为以后该型号机组结构优化，检修安排提供可靠的理论参考。

1 汽轮机疲劳损伤分析

低周疲劳是汽轮机转子疲劳损耗的主要因素[7-9]。汽轮机转子在启停过程中会产生循环的交变应力，经过一定的周次启停后，汽轮机转子表面会产生疲劳裂纹，伴随着时间的积累，转子表面裂纹会不断扩展直到断裂[10]，其特点是裂纹萌生周次少、交变频率低、循环次数一般不超过104。

研究人员把动力机械运行过程中的热应变和材料的疲劳寿命联系起来，在特定的条件下通过实验获取转子低周疲劳特性曲线(Δε-N关系曲线)。Timo-Sarney曲线是在计算低周疲劳寿命中运用较多，见图1。

图1 转子CrMoV钢的Δεt-Nf 曲线

1.1 低周疲劳寿命损耗的估算理论

在所有的ε-N曲线中，Manson-Coffine公式[11]使用最为广泛，一般表达式为[12]

(1)

Miner 理论[13]认为研究对象在应力σ1循环反复作用下，其经过N1次循环就会产生裂纹，那么经过n1次循环产生的损伤指数为n1/N1，依此类推，根据Miner理论线性累积损伤法则得出转子总的疲劳损伤指数Φf为

(2)

Miner定律运用时要求研究对象加载的载荷须是对称载荷，但是本案例所研究的对象工况为非对称工况，所以把汽轮机转子启停当作一个完整的对称的工况来分析，计算出全寿命损耗，取其一半值来作为汽轮机转子单次启动过程中的寿命损耗[14]。

(3)

式中：Φf为低周疲劳裂纹萌生寿命损耗单次启动损耗值；Nf为疲劳循环周次。

1.2 低周疲劳寿命损耗的的计算流程

合理建立有限元模型，接着加载边界条件进行转子热力耦合计算，通过计算可以得到汽轮机转子在启动过程中其应力集中部位的应力应变值，查询转子材料的低周疲劳曲线(ε-N曲线)和Timo-Sarney曲线来估算转子的疲劳寿命。求解过程见图2。

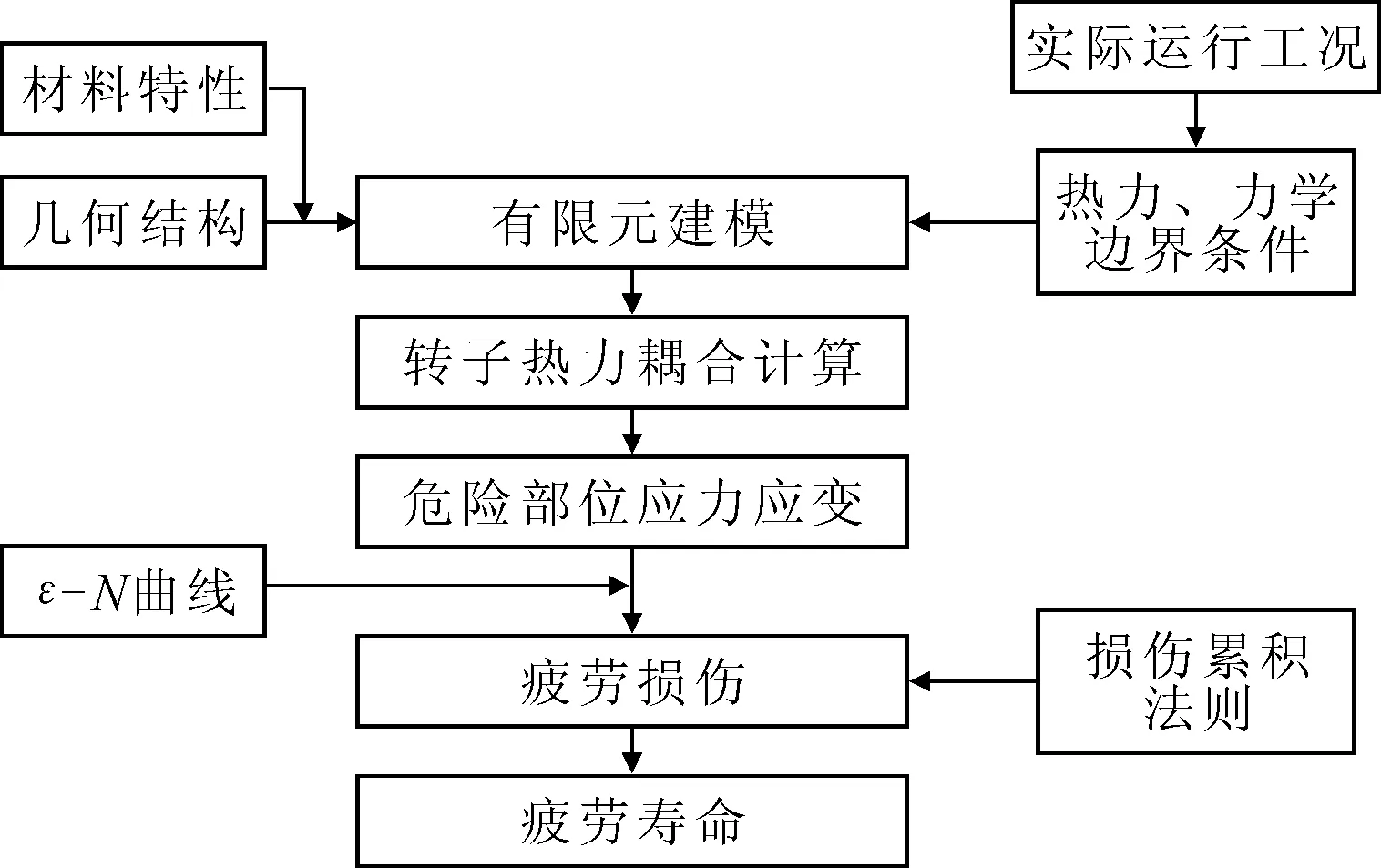
图2 转子冷态启动过程中疲劳损伤及寿命损耗计算流程

2 算例验证

2.1 转子几何模型

某国产135 MW单轴、高压、凝汽式汽轮机。其长度为5 415 mm，由12级高压段和4级中压段组成。建模时适当简化转子模型，计算时只考虑叶片在运行过程中的质量以及产生的离心力，所以将叶片简化成等效质量圆环，有利于计算的准确性[15-16]。汽轮机转子模型见图3。

图3 汽轮机转子模型

2.2 汽轮机冷态启动方案

汽轮机转子冷态启动方案见表1，汽轮机转子在前5 min内由静止加速到500 r/min，接着进行5 min的机组检查；然后进行中速暖机30 min，在此期间将转速提至1 200 r/min；接着把速度升至2 450 r/min，期间高速暖机60 r/min；最后将速度升至3 000 r/min。

2.3 转子边界条件的确定和放热系数的计算

2.3.1 热力学边界条件

1)转子在运行过程中，其左右端面不与过热器中产生的高温高压蒸汽接触，热流密度相比于高压级和中压级的叶轮小的多，所以将左右两端作为绝热面处理。

2)汽轮机转子的外表面与高温高压的蒸汽接触并且进行热量交换，所以把蒸汽在不同时刻的温度和放热系数作为第三类边界条件。

3)将轮盘两侧放热系数的平均值作为轮盘边缘的边界条件。

表1 汽轮机转子启动方案

2.3.2 转子放热系数的计算

文献[17]给出了放热系数与导热系数、转子温度、蒸汽温度的关系。

1)转子光轴部分的放热系数。

(4)

式中：h为光轴处放热系数；λc为气流导热系数；Ra为光轴外圆半径；Nu为努塞尔数。

Nu=0.1Re0.68

(5)

其中：Re为雷诺数,

(6)

其中：u为光轴外圆Ra处的圆周速度；v为气流的运动粘度。

2)叶轮两侧的放热系数。

(7)

(8)

式中：h为叶轮两侧的放热系数；Rb为光轴外圆半径；w为光轴外圆Rb处的圆周速度；Re为雷诺数(Nu为努塞尔数)，Re≤2.45×105时，Nu=0.657Re0.5；Re≥2.45×105时，Nu=0.021 7Re0.8；v为气流的运动粘度系数。

3)叶轮轮缘处的放热系数。由于将研究对象的叶片简化成等效质量圆环，难以真实准确测量轮盘边缘放热系数，所以热放系数采用平均值法先求出轮盘前后两侧的放热系数，然后将其相加求和后求平均值。

3 冷态启动过程计算与分析

根据转子初始的边界条件，将转子高压第一级叶轮和两端轴承处作为恒温点，其温度分别为280 ℃和70 ℃。通过有限元计算得到稳态温度场见图4。将得到汽轮机转子稳态温度场作为瞬态分析的初始条件，把计算得到的热力学边界条件输入有限元软件ANSYS中，得到转子启动时刻的温度场见图5。

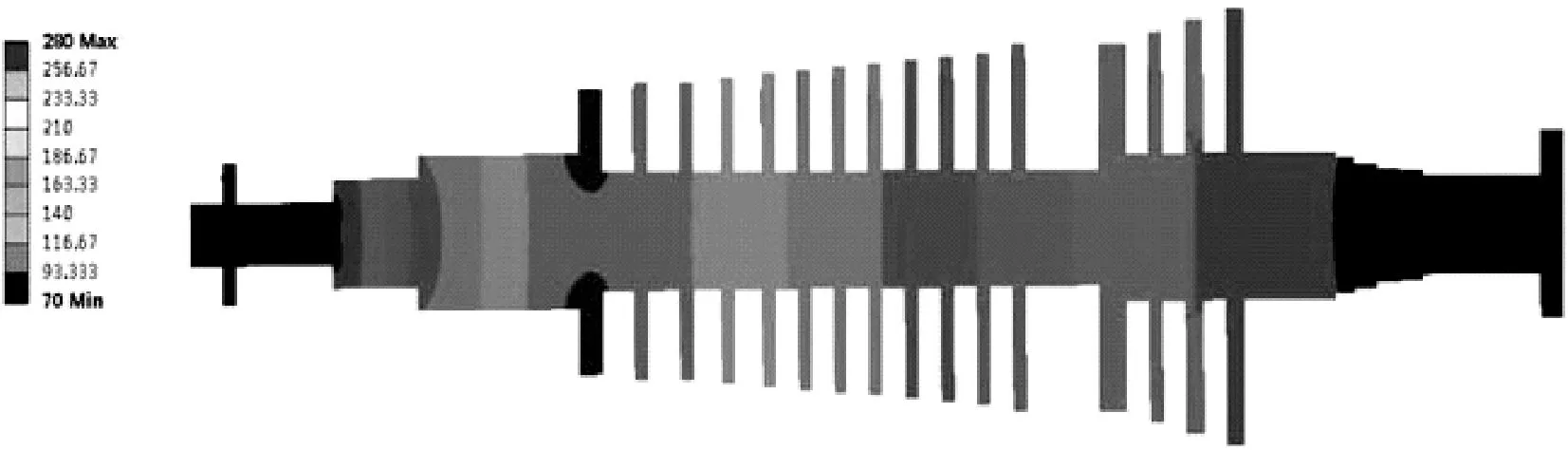
图4 高压转子启动温态温度场

图5 启动325 min时刻转子的温度场

得到转子启动时刻的温度场之后，将其作为应力求解的初始条件，同时对转子施加旋转约束，得到转子的应力云图见图6、7。

图6 启动62 min时刻转子的应力云图

图7 启动325 min时刻转子的应力云图

有限元分析发现，转子在冷态启动过程中，其易疲劳点所处的部位位于高压转子第一级叶轮根部和应力最大值为312.12 MPa。见图8、 9。

图8 冷态启动过程应力危险点应力值随时间的变化

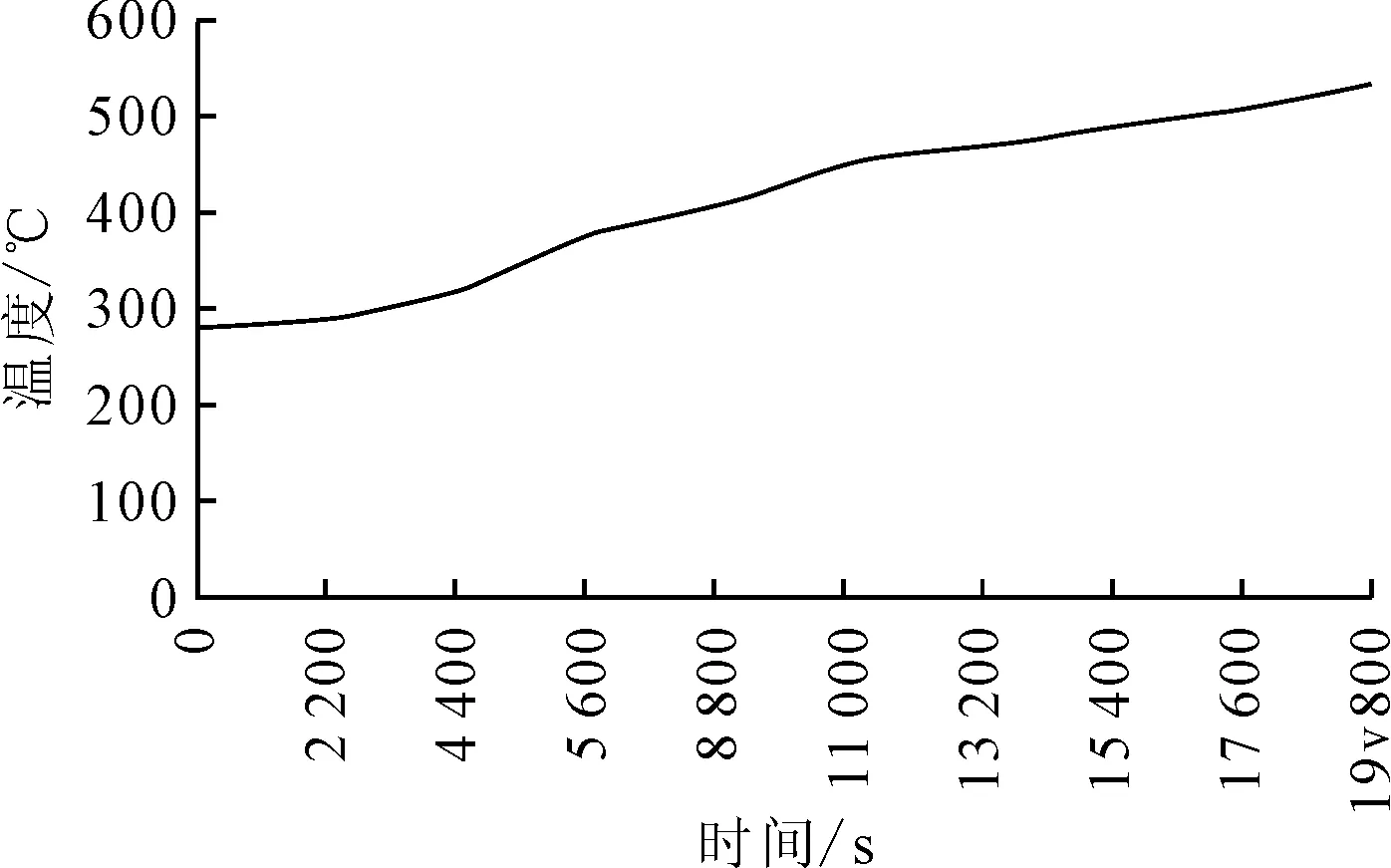
图9 冷态启动过程危险点温度随时间的变化

4 汽轮机转子低周疲劳寿命损伤计算

将危险点的公称应力和应变集中系数代入式(11)，求得汽轮机转子的全应变值，通过查询其疲劳特性曲线得到其断裂寿命循环周次，进而计算出危险点寿命损耗的百分比。根据其运行工况，取30CrMo1V转子钢在500 ℃时的弹性模量和屈服极限计算转子启动过程中的寿命损耗。(E=1.78×10-5MPa，σs=490 MPa)

4.1 计算热应力集中系数Kth

(9)

式中：σmax为热应力集中部位最大等效应力，Pa；σeq为无应力集中时光轴上的公称应力，Pa。

由图8 可见，汽轮机转子冷态启动过程中其最大集中应力312.12 MPa；公称应力254 MPa,该值是不考虑集中应力时叶根处的应力，将两个值代入公式(9)，计算得Kth=1.2。

4.2 计算屈服极限比

(10)

将σeq=254 MPa，σs=490 MPa带入到公式(10)中，计算结果为0.51。

4.3 查取塑性应变集中系数

由式(9)和(10)计算获得转子材料热应力集中系数和屈服极限比，由此查图10可获得转子材料塑性应变集中系数KS=1.0。

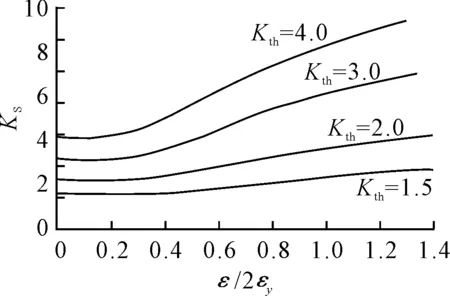
图10 塑性应变集中系数

4.4 求解应变值

(11)

数值代入，计算出应变值Δεt=0.002 8。

4.5 汽轮机转子低周疲劳寿命损耗

根据式(11)求出全应变值，查图1，得到转子循环致断周次为Nf=8 000次。计算得到Φf=0.006 25%。

查寻机械工程手册所推荐的寿命分配寿命分配值(以设计寿命30年计算)[18]，可以得到其所推荐的寿命损耗率为0.05%，远大于本文计算值，所以推测汽轮机转子冷态启动过程中，在规定的启动次数内其运行时安全的。

5 结论

1)高压转子在机组冷态启动过程中存在较大的径向温度梯度，在热应力和离心力的共同作用下，最大应力出现在高压第一级叶轮根部。汽轮机停机过程中，其应力状态与启动过程正好相反，最大应力必然集中在高压第一级叶轮根部。

2)提出一种针对汽轮机转子冷启动过程的应力分析方法。该模型基于汽轮机转子的三维实体结构，考虑汽轮机转子在启动过程中的温度变化和离心力的影响，实现汽轮机转子在冷启动过程中的瞬态动力学分析，获取危险点的等效应力。

3)结合Manson-Coffin公式、Miner线性疲劳累积损伤理论及Timo-Sarney曲线，实现对汽轮机转子冷启动疲劳寿命和寿命损耗的预测。

4)考虑现有计算机性能，本文建立的汽轮机转子模型将汽封处简化处理为光轴，因此，存在一定的模型误差。在运用线性累计法计算疲劳损伤时，忽略了热应力和离心力的相互作用影响。在今后的研究中，将提高建模的准确性，并增加预测模型的工况条件，以实现对汽轮机转子更为真实的模拟和预测。